An Alternating Direction Nonmonotone Approximate Newton Algorithm for Inverse Problems ()
1. Introduction
We consider inverse problems that can be expressed in the form
 , (1)
, (1)
where 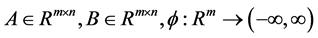 is convex, and
is convex, and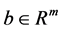 . The emphasis of our work is on problems where A and B have a specific structure. It can be applied to many applications, especially in machine learning [1] [2] , image reconstruction [3] [4] or model reduction [5] . We assume that the functions in (1) are strictly convex, so both problems has an unique solution
. The emphasis of our work is on problems where A and B have a specific structure. It can be applied to many applications, especially in machine learning [1] [2] , image reconstruction [3] [4] or model reduction [5] . We assume that the functions in (1) are strictly convex, so both problems has an unique solution .
.
In Hong-Chao Zhang’s paper [6] , he uses the Alternating Direction Approximate Newton method (ADAN) based on Alternating Direction Method (ADMM) which originaly in [7] to solve (1). He employs the BB approximation to increase the iterations. In many applications, the optimization problems in ADMM are either easily resolvable, since ADMM iterations can be performed at a low computational cost. Besides, combine different Newton-based methods with ADMM have become a trend, see [6] [8] [9] , since those methods may achieve the high convergent speed.
In alternating direction nonmonotone approximate Newton (ADNAN) algorithm developed in this paper, we adopt the nonmonotone line search to replace the traditional Armijo line search in ADAN, because the nonmonotone schemes can improve the likelihood of finding a global optimum and improve convergence speed in cases where a monotone scheme is forced to creep along the bottom of a narrow curved valley in [10] .
In the latter context, the first subproblem is to solve the unconstrained minimization problems with Alternating Direction Nonmonotone Approximate Newton algorithm. The purpose is to accelerate the speed of convergence, and then to project or the scale the unconstrained minimizer into the box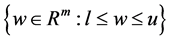 , The second subproblem is a bound-constrained optimization problem.
, The second subproblem is a bound-constrained optimization problem.
The rest of the paper is organized as follows. In Section 2, we give a review of the alternating direction approximate Newton method. In Section 3, we introduce the new algorithm ADNAN. In Section 4, we introduce the gradient-based algorithm of the second subproblem. A preliminary convergence analysis for ADNAN and gradient- based algorithm (GRAD) is given in Section 5. Numerical results presented in Section 6 explain the effectiveness of ADNAN and GRAD.
2. Review of Alternating Direction Approximate Newton Algorithm
We introduce a new variable w to obtain the split formulation of (1):
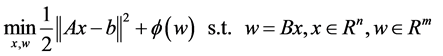 (2)
(2)
The augmented Lagrangian function associated with (2) is
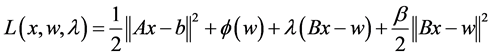 (3)
(3)
where 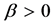 is the penalty parameter,
is the penalty parameter, 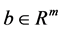 is a Lagrangian multiplier associated with the constraint
is a Lagrangian multiplier associated with the constraint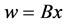 . In ADMM, each iteration minimizes over x holding w fixed, minimizes over w holding x fixed, and updates an estimate for the multiplier b. More specifically, if
. In ADMM, each iteration minimizes over x holding w fixed, minimizes over w holding x fixed, and updates an estimate for the multiplier b. More specifically, if 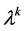 is the current approximation to the multiplier, then ADMM [10] [11] applied to the split formulation (3) is given by the iteration:
is the current approximation to the multiplier, then ADMM [10] [11] applied to the split formulation (3) is given by the iteration:
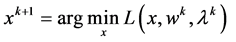 (4)
(4)
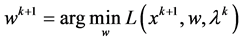 (5)
(5)
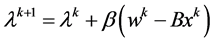 (6)
(6)
And (4) can be written as follows:

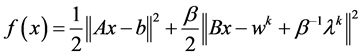 (7)
(7)
For any Hermitian matrix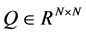 , we define
, we define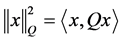 , if Q is a positive definite matrix, then
, if Q is a positive definite matrix, then ![]() is a norm. The proximal version of (4) is
is a norm. The proximal version of (4) is
![]()
![]() (8)
(8)
In ADAN, the choice ![]() will cancel the
will cancel the ![]() term in this iteration while
term in this iteration while ![]() is retained. We replace
is retained. We replace ![]() by
by![]() , where
, where ![]() is a Barzilai-Borwein (BB) [8] [12] approximation to
is a Barzilai-Borwein (BB) [8] [12] approximation to![]() . We can observe the fast convergence of BB approximation in the experiments of Raydan and Svaiter [13] . Moreover,
. We can observe the fast convergence of BB approximation in the experiments of Raydan and Svaiter [13] . Moreover, ![]() is strictly smaller than the largest eigenvalue of
is strictly smaller than the largest eigenvalue of![]() , and
, and ![]() is indefinite, so the new convergence analysis is needed. As a result, the updated version for x given in (4) can be expressed as follows:
is indefinite, so the new convergence analysis is needed. As a result, the updated version for x given in (4) can be expressed as follows:
![]() (9)
(9)
![]() (10)
(10)
Here, ![]() is the generalized inverse,
is the generalized inverse, ![]() is the Hessian of the objective
is the Hessian of the objective![]() , and
, and ![]() is the gradient of
is the gradient of ![]() at
at![]() ,
,![]() . The formula for
. The formula for ![]() in (2) is exactly the same formula that we would have gotten if we performed a single iteration of Newton’s method on the equation
in (2) is exactly the same formula that we would have gotten if we performed a single iteration of Newton’s method on the equation ![]() with starting guess
with starting guess![]() . We employ the BB approximation
. We employ the BB approximation![]() , [14] where
, [14] where
![]()
and ![]() is a positive lower bound for
is a positive lower bound for![]() . Hence, the Hessian is approximated by
. Hence, the Hessian is approximated by![]() . Since a Fourier transform can be inverted in
. Since a Fourier transform can be inverted in ![]() flops. The inversion of
flops. The inversion of ![]() can be accomplished relatively quickly. After replacing
can be accomplished relatively quickly. After replacing ![]() by
by![]() , the iteration becomes
, the iteration becomes ![]() where
where ![]()
Note that by substituting ![]() in (2) and solving for the minimizer, we would get exactly the same formula for the minimizer as that given in (5). When the search direction is determined suitable step size
in (2) and solving for the minimizer, we would get exactly the same formula for the minimizer as that given in (5). When the search direction is determined suitable step size ![]() along this direction should be found to determine the next iterative point such as
along this direction should be found to determine the next iterative point such as![]() .
.
The inner product between ![]() and the objective gradient at
and the objective gradient at ![]() is
is
![]() .
.
It follows that ![]() is a descent direction. Since
is a descent direction. Since ![]() is a quadratic, the Taylor expansion of
is a quadratic, the Taylor expansion of ![]() around
around ![]() is as follows:
is as follows:
![]()
where ![]()
In this section, we adopt a nonmonotone line search method [9] . The step size ![]() is chosen in an ordinary Armijo line search which could not admit the more faster speed in unconstrained problems [12] . In contrast, nonmonotone schemes can not only improve the likelihood of finding a global optimum but also improve convergence speed.
is chosen in an ordinary Armijo line search which could not admit the more faster speed in unconstrained problems [12] . In contrast, nonmonotone schemes can not only improve the likelihood of finding a global optimum but also improve convergence speed.
Initialization: Choose starting guess![]() , and parameters
, and parameters![]() ,
, ![]() , and
, and![]() . Set
. Set![]() ,
, ![]() , and
, and![]() .
.
Convergence test: If ![]() sufficiently small, then stop.
sufficiently small, then stop.
line search update: set![]() ,where
,where ![]() satisfies either the (non- monotone) Wolfe conditions:
satisfies either the (non- monotone) Wolfe conditions:
![]() (11)
(11)
![]() (12)
(12)
or the (nonmonotone) Armijo conditions:![]() , where
, where ![]() is the trial step, and
is the trial step, and ![]() is the largest integer such that (11) holds and
is the largest integer such that (11) holds and![]() .
.
Cost update: Choose![]() , and update
, and update
![]() (13)
(13)
Observe that ![]() is a convex combination of Ck and
is a convex combination of Ck and![]() . Since
. Since ![]() it follows that Ck is a convex combination of the function values
it follows that Ck is a convex combination of the function values![]() . The choice of
. The choice of ![]() controls the degree of nonmonotonicity. If
controls the degree of nonmonotonicity. If ![]() for each k, then the line search is the usual monotone Wolfe or Armijo line search. If
for each k, then the line search is the usual monotone Wolfe or Armijo line search. If ![]() for each k,
for each k,
then ![]() where
where![]() , is the average function value. The
, is the average function value. The
scheme with ![]() was proposed by Yu-Hong Dai [15] . As
was proposed by Yu-Hong Dai [15] . As ![]() approaches 0, the line search closely approximates the usual monotone line search, and as
approaches 0, the line search closely approximates the usual monotone line search, and as ![]() approaches 1, the scheme becomes more nonmonotone, treating all the previous function values with equal weight when we compute the average cost value
approaches 1, the scheme becomes more nonmonotone, treating all the previous function values with equal weight when we compute the average cost value![]() .
.
Lemma 2.1 If ![]() for each k, then for the iterates generated by the nonmonotone line search algorithm, we have
for each k, then for the iterates generated by the nonmonotone line search algorithm, we have ![]() for each k. Moreover, if
for each k. Moreover, if ![]() and
and ![]() is bounded from below, then there exists
is bounded from below, then there exists ![]() satisfying either the Wolfe or Armijo conditions of the line search update.
satisfying either the Wolfe or Armijo conditions of the line search update.
3. Alternating Direction Nonmonotone Approximate Newton Algorithm
In Algorithm 1, we could get the x at each iteration which can be combined with Algorithm 2. Then, we use the Algorithm 2 to solve the first subproblem in this paper which is an unconstrained minimization problem with ADNAN, then to project or the scale the unconstrained minimizer into the box
![]() (14)
(14)
the iteration is as follows:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
Later we give the existence and uniqueness result for (1).
The solution ![]() to (5) has the closed-form means
to (5) has the closed-form means
![]()
with P being the projection map onto the box ![]()
Algorithm 2. Alternating Direction Nonmonotone Approximate Newton algorithm.
Parameter:![]() , Initialize
, Initialize ![]()
Step 1: If ![]() sufficiently small, then set
sufficiently small, then set![]() , and branch to Step 4.
, and branch to Step 4.
![]() ,
, ![]()
Step 2: If ![]() then
then ![]()
Step 3: If ![]() accomplish the Wolfe conditions, then
accomplish the Wolfe conditions, then ![]()
Step 4: Update x which generated from Algorithm 1.
Step 5: ![]()
Step 6: ![]()
Step 7: If a stopping criterion is satisfied, terminate the algorithm, Otherwise k = k + 1 and go to Step 1.
Lemma 3.1: we show some criteria that are only satisfied a finite number of times, so ![]() converge to positive limits. An upper bound for
converge to positive limits. An upper bound for ![]() is the following:
is the following:
Uniformly in k, we have ![]() where
where ![]() is the value of
is the value of ![]() at the start of iteration k and
at the start of iteration k and ![]() is the starting
is the starting ![]() in ADAN.
in ADAN.
Lemma 3.2: If![]() , then
, then ![]() minimizes
minimizes ![]()
4. Algorithm 3: Gradient-Based Algorithm (GRAD)
Next, we consider the second subproblem which is about bound-constrained optimization problem as
![]() (18)
(18)
And the iteration is similar with (4) (5) (6) as follows:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Compute the solution ![]() from (19),
from (19), ![]()
Compute the solution ![]() from (20),
from (20), ![]()
Set ![]()
5. Convergence Analysis
In this section, we show the convergence of proposed algorithms. Obviously, the proofs of the two algorithms are almost the same, and we only prove the convergence of algorithm 2.
Lemma 3.1: Let L be the function in (3). The vector ![]() solves (2) if and only if there exists
solves (2) if and only if there exists ![]() such that
such that ![]() solves
solves
![]()
Lemma 3.2: Let L be the function in (3), ![]() be a saddle-point of L, Then
be a saddle-point of L, Then
the sequence ![]() satisfies
satisfies![]() .
.
Theorem 3.1: Let ![]() be the sequence of iterates produced by the algorithm 2.
be the sequence of iterates produced by the algorithm 2.
then![]() ,
, ![]() and
and ![]() is the optimal point for problem (14)
is the optimal point for problem (14)
Proof From Lemma 3.1, 3.2, we obtain that
![]() (22)
(22)
Since we have a unique minimizer in![]() , so we have
, so we have![]() , Then, (22) gives
, Then, (22) gives ![]() which completes the proof.
which completes the proof.
6. Numerical Experiments
6.1. Parameter Settings
In Algorithm 2, the parameters![]() , the penalty in the augmented Lagrangian (3), are common to these two algorithms, ADAN and ADNAN. Besides
, the penalty in the augmented Lagrangian (3), are common to these two algorithms, ADAN and ADNAN. Besides ![]() has a vital impact on convergence speed. We choose
has a vital impact on convergence speed. We choose ![]() based on the results from W. Hager [6] . The choice
based on the results from W. Hager [6] . The choice ![]() is a compromise between speed and stability,
is a compromise between speed and stability, ![]() is large enough to ensure invertibility.
is large enough to ensure invertibility.
The search directions were generated by the L-BFGS method developed by No-cedal in [16] and Liu and Nocedal in [1] . We choose the step size ![]() to satisfy the Wolfe conditions with m = 0.09 and σ = 0.9. In addition we employ a fixed value
to satisfy the Wolfe conditions with m = 0.09 and σ = 0.9. In addition we employ a fixed value ![]() which could get the reasonable results. To obtain a good estimate for the optimal objective in (1), we ran them for 100,000 iterations. The optimal objective values for the three data sets were
which could get the reasonable results. To obtain a good estimate for the optimal objective in (1), we ran them for 100,000 iterations. The optimal objective values for the three data sets were
![]()
In addition, we timed how long it took ADNAN to reduce the objective error to within 1% of the optimal objective value. The algorithms are coded in MATLAB, version 2011b, and run on a Dell version 4510U with a 2.8 GHz Intel i7 processor.
In Algorithm 3, a 256-by-256 gray-scale image was considered, which is compared to the experiment by J. Zhang [8] . The dimensions of the inverse problems are m = n = 65536 and the constraints are ![]() and
and![]() . The experiments on image deblurring problems show that GRAD algorithm is also effective in terms of quality of the image resolution.
. The experiments on image deblurring problems show that GRAD algorithm is also effective in terms of quality of the image resolution.
6.2. Experiments Results
This section compares the performance of the ADNAN to ADAN. The main difference between the ADNAN algorithm and the ADAN algorithm is the computation of![]() . In ADAN
. In ADAN ![]() where
where ![]() is the step size. In ADNAN, x generated from Algorithm 1, if the convergence condition in ADAN is satisfied, then the update
is the step size. In ADNAN, x generated from Algorithm 1, if the convergence condition in ADAN is satisfied, then the update ![]() could be performed. Here
could be performed. Here ![]() is the same choice for them. Hence, there seems to be a significant benefit from using a value for
is the same choice for them. Hence, there seems to be a significant benefit from using a value for ![]() smaller than the largest eigenvalue of
smaller than the largest eigenvalue of![]() .
.
The initial guess for![]() ,
, ![]() and
and ![]() was zero for two algorithms. Figures 1-3 show the objective values and objective error as a function of CPU time. Moreover, we give the comparison of objective values and objective error versus CPU time/s for different
was zero for two algorithms. Figures 1-3 show the objective values and objective error as a function of CPU time. Moreover, we give the comparison of objective values and objective error versus CPU time/s for different ![]() conditions. It is observed that ADNAN is slightly stable than ADAN although ADNAN and ADAN are competitive. The ADNAN not only could get more smaller objective error but also get more fast convergence speed (see Figure 3). In addition, ADNAN objective value could get more smaller after a few iterations than ADAN. As a whole, the effect of ADNAN is superior to ADAN.
conditions. It is observed that ADNAN is slightly stable than ADAN although ADNAN and ADAN are competitive. The ADNAN not only could get more smaller objective error but also get more fast convergence speed (see Figure 3). In addition, ADNAN objective value could get more smaller after a few iterations than ADAN. As a whole, the effect of ADNAN is superior to ADAN.
On the other hand, the experiment results about Algorithm 3 are as follows:
Original image blurry image deblurred image
Original image blurry image deblurred image
Original image blurry image deblurred image
Original image blurry image deblurred image
7. Conclusions
According to the Figures 1-3, we can conclude that the nonmonotone line search could accelerate the convergence speed, furthermore ADNAN could get the objective values more stable and fast during the iterations when compared to ADAN.
On the other hand, the validness of GRAD is verified. Experiments results on image deblurring problems in Figures 4-7 show that difference constraints on x can also get effective deblurred images.
Acknowledgements
This work is supported by Innovation Program of Shanghai Municipal Education Commission (No. 14YZ094).