Analysis of Higher Order System with Impulse Exciting Functions in Z-Domain

Branislav Dobrucký¹, Pavol Štefanec¹, Mariana Beňová¹, Oleg V. Chernoyarov², Michal Pokorný¹

¹Faculty of Electrical Engineering, University of ?ilina, ?ilina, Slovak Republic.
²Department of Radio Engineering Devices and Antenna Systems, National Research University, Moscow Power Engineering Institute, Moscow, Russia.

DOI: 10.4236/cs.2016.711328                

Abstract

This paper deals with mathematical modelling of impulse waveforms and impulse switching functions used in electrical engineering. Impulse switching functions are later investigated using direct and inverse z-transformation. The results make possible to present those functions as infinite series expressed in pure numerical, exponential or trigonometric forms. The main advantage of used approach is the possibility to calculate investigated variables directly in any instant of time; dynamic state can be solved with the step of sequences (T/6, T/12) that means very fast. Theoretically derived waveforms are compared with simulation worked-out results as well as results of circuit emulator LT spice which are given in the paper.

Keywords

Impulse Systems, Switching Function, Z-Transformation, Inverse Z-Transformation, Steady State Operation, Dynamical State Model, Modelling and Simulation

1. Introduction

It is known that periodical non-harmonic discontinuous function is possible to portray in compact closed form using Fourier infinite series [1] [2] . One of the lesser known methods is using of Fischer-Turbar definition of for the main value

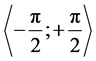based on a standardization of trigonometric function modulo π [3] - [5] . So,

increasing saw-tooth function with angular frequency 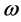can be expressed in closed form

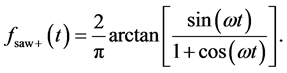(1)

It is also possible to express the rectangular waveform using Laplace or Laplace- Carson transform but inverse transform is not easy calculation, particularly for higher order systems. Classical solution leads to results in Fourier series form, otherwise the Heaviside calculus is to be used [2] , [6] .

Assuming finite switch-on and switch-off times of real-time waveforms the normalized derivative impulse function for given waveforms can be created [7] , Figure 1.

Further, based on zero order hold function and unipolar modulation [8] - [10] , the switch-off impulses will be substituted by zero points, and result waveforms can be presented as follow from, Figure 2.

The impulse switching functions as in Figure 2 can be easily described in Z-domain using basic definitions and rules of Z-transformation.

2. Description of Impulse Switching Functions in Z-Domain

Using basic definition of Z-transform-taking into account z-images of constant and alternating series and based on the rules of the Z-transform it can be written [10] .

Figure 1. Normalized derivative impulse function of: rectangular waveform with half- width-pulse.

Figure 2. Impulse switching functions with unipolar control of: rectangular waveform with half width.

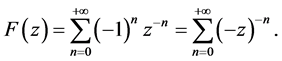
The sum of that geometric series with quotient 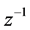is

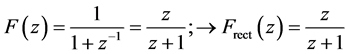(3)

where root of the denominator is.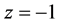

For inverse Z-transform 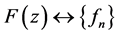one can use different methods [11] :

Cauchy integral residua theorem [12]

(4)

where; N is number of poles of denominator and 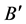is derivative of denominator

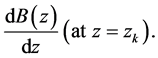(5)

Taking example

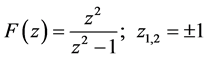(6)

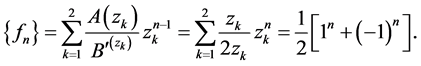(7)

Applying inverse Z-transform for converter output phase voltages in Z-domain one can create impulse switching functions. Residua theorem described above can be used for inverse Z-transform .

Let’s consider following different discontinuous type of waveforms:

2.1. Impulse Functions of Rectangular Half Width Waveform

Using theorem for displacement in the Z-transformation [10] [11]

(8)

the Z-image of the 1/2-pulse length rectangular waveform will be:

(9)

where roots of the denominator are placed on boundary of stability in unit circle [1] , [10] , Figure 3(a).

Applying inverse Z-transform one can write

(10)

(a) (b) (c)

Figure 3. Pole placements of denominator polynomials of (a); (b) and (c).

This result can be expressed in different forms: purely numerical-, exponential-, and trigonometric ones

(11)

The all poles of denominator polynomials are placed on boundary of stability of unit circle and can be used for further analytic solution.

2.2. Pulse Modulated Waveforms

2.2.1. Three-Pulse Modulated Waveform

Above given approach can also be used for rectangular waveform with half-width of the pulse. Graphical interpretation of this switching function is shown in the Figure 4(a).

Z-transform image of that function will be:

(12)

Formula for voltage impulse sequence can also be worked-out by inverse z-transform using the lema for residua.

(13)

where roots of the polynomial are

(a)(b)

Figure 4. Impulse switching function worked-out using (a) and (b).

see Figure 3(b).

(14)

Proof within the frame of one half period:

So, q.e.d.

2.2.2. Three-Phase Impulse Waveform

The Z-image for three-phase system with discontinuous waveform, Figure 4(b), is

(15)

where roots of the denominator are, Figure 3(c).

Applying inverse Z-transform for this three-phase system

(16)

After adapting

(17)

Formula (17) can be expressed in exponential form

and also in trigonometric one

(18)

Proof within the frame of one time period:

So, q.e.d.

Presented in figure worked-out sequences express impulse nature and represent the impulse switching functions which can be easily described in Z-domain using basic definitions and rules of Z-transformation. From the Figure 4(c) and pole displacement of three-phase impulse system, Figure 3(c) implies that it will feature by 2N-mul- tiple symmetry and therefore analysis can be done within one T/6-th of time period [13] .

3. Modelling and Simulation of 2nd Order System with Non-Harmonic Periodical Exciting Functions Based on ISF

Dynamical state model of the systems include exciting functions as an input vector. The models can be expressed in a continuous form:

(19)

or discrete form, respectively

(20)

where k is order of computation step (not the step of sequence).

Discrete form of state space model of the investigated system with the step of impulse switching function can be obtained directly from the impulse switching functions generated above:

(21)

where the step is equal to the step or period, respectively to the impulse sequences of switching functions. So, when is equal e.g. π/6 i.e. T/12 (see Equation (17)) then

(22)

where by Chap. 2, Figure 3(a) and it is

(23)

Determining and matrix coefficients one can calculate the vector of system state variable in discrete time instants, i.e. in the multiple of.

3.1. Calculation of, Matrix Coefficients

These can be calculated using analytical method (suitable for systems of low orders); numerical method:

(24)

where should be determined either analytically or numerically or experimentally in very small time instant; discrete method using Z-transform

and can be determined as above; experimental method by measuring of state-variable at the time instant.

Describing discrete determination method using Z-transform-by iterative process.

As mentioned, recursive formula

(25)

with where a are discrete impulse responses of state-va- riables gained by any of computation (above) or identification method [14] , is calculation step, works with discretized time

(26)

Calculation step should be short enough e.g. or step of the sequence. Usually, equal 1 - 2 el. Decomposing the state Equation (16) into two scalar equations yields

(27)

where under understanding electrical L-C//R circuitry with parameters Figure 5:

:

Figure 5. Schematics of L-C//R circuitry.

Time discretization using Euler explicit method:

(28)

where is calculation (integration) step.

Then, taking as above one gets for

and

.

Taking equal to 0.0001 sec the coefficients and are, respectively

So, in matrix form

(29)

Regarding to:

Replacing n in Equation (23) by

one gets (30)

(31)

where “fix” is notation for rounding of numbers to zero [15] .

Based on total mathematical induction it can be derived with the help from [16] ,

(32)

derivation of this formula see below. Then

(33)

Using Equation (28) the determination of will be possible using, see Figure 6(a) and Figure 6(b).

After choosing, k will be the in the range of 0 - 30, thus

(34)

(a)(b)

Figure 6. To determination of (a); (b).

and

(35)

Then

(36)

(37)

Finally the values are

(38)

3.2. Calculation of State Variable Values

Since

Thus

(39)

(40)

Calculated sequences and of, state variables are given in Table 1. The values of state-variables, in the frame of one half period are presented in detail in Table 2.

The sequences and of, state variables are also depicted in Figure 7, interconnected by polynomial of the 1st order because of continuous quantities.

Let’s note that values of state variables and calculated with step can be presented as sequences (a) or time waveforms, with bonding points by linear interpolation (b); verificated by LT Spice emulator (c).

3.3. Alternative Way of, Matrix Coefficients Calculation and State Variable Values Calculation

The same result can be obtained by numerical solution using explicit or implicit Euler

(a)(b)(c)

Figure 7. Waveforms of sequences of, (a) and state variables, (b) and verification (c).

Table 1. State variable values during the first period after switching the load on.

Table 2. Proof within the frame of one half period.

method for the second order system with integration step and taking in account the same time instants:

So, sequences are similarly the same as calculated using Equation (39) q.e.d.

The sequences and can also be worked-out using Z-transform of Equation (22)

(41)

where

(42)

By adapting

(43)

Or, by decomposition of into two scalar equations

(44)

(45)

where and

(46)

And applying Z-transform

(47)

(48)

where is the same as above.

So, and can be derived and separated:

Since it flows from Equation (47), (48)

(49)

and

(50)

Executing an inverse Z-transform of Equations (32), (33) or (29) one obtains

(51)

where n is a number of roots of the polynomial of denominator of, i.e. of, and are roots of the of equation

Similarly

(52)

with the same roots as of above. Those lead to sequences and worked-out and given in Table 1 or Figure 6, respectively.

But, it can be seen, that this method using residua theorem is rather arduous because of need of evaluation of denominator of.

3.4. Behaviour of the System

System behaviour during transient for longer time-practically up to the steady state can be describe using Equation (18), (10) and theory given in [15] with computation step:

For

, , ,

be valid

(53)

By graduated calculation and using mathematical induction the general relation can be derived

(54)

(55)

Behaviour of the system under load switched-on during 8 periods, i.e. 96 of T/12 is shown in Figure 8.

Another way using computation step Δ leads to

(56)

and using above approach

(57)

where

(58)

Figure 8. Transient of the 2nd order system under impulse exciting function with the step of T/12.

Behaviour of the system under load switched-on during 8 periods, i.e. 2880 of k is shown in Figure 9.

Let’s note that values of state variables and are drawn with computation step connected by linear interpolation, too.

Confirmation of transient behavior using the fundamental harmonic method:

Analytical calculation of Fourier coefficient [2] , [11] :

(59)

Taking in account symmetry of impulse waveform the magnitude of fundamental harmonic will be

(60)

This is the same value as can be obtained using Equation (34), [17]

(61)

where

―is order of harmonics;

2N―number of pulses in period;

―relative pulse width 0 - 1;

―supply voltage of the 3-phase inverter.

Figure 9. Transient of the 2nd order system under impulse exciting function with the step of T/360.

For:

(62)

what indicates equality of both calculations.

Now, one can use the harmonic voltage with magnitude as exciting function applied to system (19).

(63)

Behaviour of the system under load switched-on during 8 periods, i.e. is shown in Figure 10.

Let’s note that values of state variables, and also are drawn with computation step under method of fundamental harmonics while impulse waveform of supply voltage was substituted by its fundamental harmonic.

Verification of transient behavior using circuit emulator LT Spice:

Verification of transient behavior was done using circuit LT Spice emulator. The scheme of electronic circuitry is shown in Figure 11. Schematics of R-L-C load is being shown in Figure 5.

The result is shown in Figure 12.

Let’s note that values of state variables, and also have been obtained from circuit emulator with the same sampling as computation step used above.

By comparing Figures 8-10 and Figure 12 one can conclude that behaviour of the system-step switching-on of impulse discontinuous exciting function-calculated by different methods is practically the same. Transient waveforms show that the over-shoot during the first period is around multiple 2, and settling time of the transient is about 10 periods.

Figure 10. Transient under harmonic supplying voltage using fundamental harmonic method with the step of T/360.

Figure 11. Schematics of generating modulated impulse voltage in LT spice environment.

Figure 12. Transient of the 2nd order system under impulse exciting function verificated by LT spice.

4. Conclusion

The method given in the paper demonstrated how is possible to write impulse switching functions which can be describable by z-transformation by application of unipolar modulation and zero order function. Results presented in paper demonstrated exceptionality of the formulated method―calculation of variable quantities of investigated linear dynamical system at any time, without knowing the values of foregoing time(s). This is not possible in case of pure numerical computing. Moreover, dynamical state can be solved very fast using step of calculation equal step of sequences (T/6, T/12). Comparing results worked-out by four different methods one can see that they reached waveform practically the same. Presented techniques are suitable for analysis of both transient and steady-state behaviour of investigated system mainly in electrical engineering.

Acknowledgements

The paper was supported from R&D operational program Centre of excellence of power electronics systems and materials for their component No OPVaV-2008/2.1/01- SORO ITMS 26220120003, and also from Slovak Grant Agency VEGA by the grant No 1/0928/15.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Aramovich, J.G., Lunts, G.L. and Elsgolts, L.C. (1973) Functions of Complex Variable, Operator Calculus, Stability Theory. Alfa, Bratislava. (In Russian, Translated into Slovak)
[2]	Beerends, R.J., Morsche, H.G., Berg, J.C. and Vrie, E.M. (2003) Fourier and Laplace Transforms. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511806834
[3]	Takeuchi, T.J. (1968) Theory of SCR Circuit and Application to Motor Control. Electrical Engineering College Press, Tokyo.
[4]	Turbar, K.A. (1972) Representation of Discontinuous Periodical Currents and Voltages under Their Developing into the Series. ETZ, 93, 57-60. (In German)
[5]	Fischer, J. (1972) Lectures on arc0tan for the Main Value Based on a Standardization of Trigonometric Functions. University of Karlsruhe (KIT), Karlsruhe. (In German)
[6]	Dobrucky, B., Chernoyarov, O.V. and Mar?oková, M. (2015) Computation of the Total Harmonic Distortion of Impulse System Quantities Using Infinite Series. Proceedings of 14th Conference on Applied Mathematics, STU Bratislava, 3-5 February 2015, 213-220.
[7]	?tefanec, P., Beňová, M., Dobrucky, B. and Chernoyarov, O.V. (2015) Generating and Mathematical Modelling of Discontinuous Impulse Waveforms. Proceedings of the 2015 International Conference on Modeling, Simulation and Applied Mathematics (MSAM), Phuket, 23-24 August 2015, 330-335. http://dx.doi.org/10.2991/msam-15.2015.76
[8]	Dobrucky, B., Pokorny, M. and Beňová, M. (2014) On Impulse Switching Functions of Inverters as an Orthogonal System. Journal of Mathematics and System Science, 4, 743-749.
[9]	Dobrucky, B., Pokorny, M., Beňová, M. and Abdamula, M.A.R. (2013) Modeling of Power Converters Using Z-Transform. Communication. Scientific Letters of the University of Zilina, 15, 43-47.
[10]	Vích, R. (1983) Z-Transformation and Some of Its Utilization. SNTL Mathematical Seminar, Prague. (In Czech)
[11]	Goeldner, K. (1982) Mathematical Basics of System Analysis [In German: Mathematische Grundlagen der Systemanalyse]. Vol. 2, VEB Fachbuchverlag, Leipzig.
[12]	Blagouchine, I.V. and Moreau, E. (2011) Analytic Method for the Computation of the Total Harmonic Distortion by the Cauchy Method of Residues. IEEE Transactions on Communications, 59, 2478-2491. http://dx.doi.org/10.1109/TCOMM.2011.061511.100749
[13]	Dobrucky, B., Mar?oková, M. and Pokorny, M. (2010) Chapter 9: Minimum Data Acquisition Time for Prediction of Periodical Variable Structure System. In: Vardusi, M., Ed., Data Acquisition, SCIYO Publisher, Rijeka, 169-184.
[14]	Sj?berg, J., et al. (1995) Non-Linear Black-Box Modeling in System Identification: A Unified Overview. Automatica, 31, 1691-1724. http://dx.doi.org/10.1016/0005-1098(95)00120-8
[15]	Palamides, A. and Veloni, A. (2011) Signals and Systems Laboratory with Matlab. CRC Press, Boca Raton.
[16]	Strejc, V. (1978) State-Space Theory of Linear Discrete Control. Academia Publisher, Prague. (In Czech)
[17]	Bednárik, B. and Vittek, J. (1979) Fourier Harmonic Analysis of the Inverter Output Voltage with PWM Control. Elektrotechnicky Obzor, 68, 461-465. (In Slovak)