Planar Retro-Reflector for Grazing Incident Beam of High-Energy X-Ray Photons

Hakob Jacob Bezirganyan^1,2*, Robert Bezirganyan^1,3*, Siranush Bezirganyan^1,4

¹X-Ray Optical Memory, Inc., Bellevue, WA, USA.
²V Group Inc., Cranbury, NJ, USA.
³University of Washington, Bothell, WA, USA.
⁴Bellevue College, Main Campus, Bellevue, WA, USA.

DOI: 10.4236/jamp.2016.49181                

Abstract

The grazing-incidence hard X-ray retro-reflector (GIRR) is a novel optical element, which completely suppresses the conventional mirror beam in the retro-reflection mode, and, at the same time, totally reflects the primary grazing incident X-radiation backwards to its source in strictly anti-parallel direction with minimal scattering. The GIRR is a good alternative to hard X-ray normal-incidence Bragg mirror, and has a high potential for applications in various X-ray optical devices and techniques, such as, hard X-ray optical noise (or background) filters, high-quality hard X-ray waveguides, low-gain hard X-ray free electron laser resonators (XFELRs), X-ray holography, coherent X-ray diffraction imaging, phase-contrast imaging, as well as in hard X-ray optical data storage devices and deep space hard X-ray communications. The proposed optical element consists of single-crystal wafer covered by a thin, non-diffracting layer of low-absorbing material.

Keywords

X-Ray, Diffraction Theory, Single-Crystal, Total Retro-Reflection, Mathieu Functions

1. Introduction

The development of high quality hard X-ray retro-reflectors is important, since the later they can be used in solving of various challenges facing modern advanced hard X-ray optical engineering.

During the last two decades, there has been an essential progress in the design, modelling, fabrication and applications of optical retro-reflectors [1] - [5] , especially, in the sphere of the evolving technology and applications in optical wireless communications (OWC) from short to long distances [6] - [9] .

However, the direct extension for existing technologies from optical region to shorter X-ray wavelengths is not possible. The retro-reflection techniques developed for visible light don’t work for hard X-ray wavelengths because the refractive index of X-rays is slightly less than the unity for most substances. A common way to overcome this problem is through the application of various X-ray diffraction methods [10] - [13] .

Consider the well-known technique of normal-incidence hard X-ray Bragg reflection [14] - [18] which is utilized in, for example, simple two-crystal plate cavity [19] - [24] , as well as in multi-cavity [25] [26] Fabry-Perot (FP) resonators when the magnitude of Bragg angle 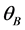is close to 90˚. The cavities are separated by the crystal plates with specific thickness ratios and, basically, have a common monolithic crystal base. These plates act as a normal-incidence backward reflecting Bragg mirrors. However, such resonators require a stringent temperature control, since the crystal plates themselves are affected by thermal expansion, which, in its turn, leads to a problem of non-stability in lattice parameter of the diffracting planes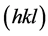. The overall uncertainty in modern measurements of, for example, the Si lattice parameter is 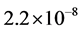and thermal expansion at 22.5˚C is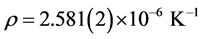. Therefore, it is desirable to know the crystal temperature well enough, and have it controlled precise enough, to keep the Si lattice constant 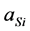unchanged within 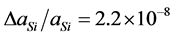accuracy. According to above conditions, the temperature accuracy 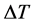should not exceed the following value of 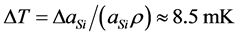[27] - [29] .

The absorption, and, consequently, the crystal plate heating problem are partially solved in [23] , where, instead of a conventional cavity with normal incidence, the authors of paper [23] use an inclined incident beam along one of the multiple diffraction directions to generate back diffraction in a resonator cavity. To address to change in the angle of incidence, authors remove the absorption in the first crystal, in contradiction to conventional normal-incidence one-cavity FR resonators setup.

2. Total Retro-Reflection of Grazing Incident X-Rays

In this paper, the authors propose and investigate the grazing-incidence hard X-ray backward reflector or retro-reflector (GIRR), which totally reflects the primary grazing incident X-radiation backwards to its source in strictly anti-parallel direction with minimal scattering.

The authors overcome the retro-reflector’s thermal expansion problem by using the X-ray grazing-incidence diffraction scheme, based on the fact that the X-ray penetration depths in a crystal are at least in three orders smaller than in the case of a normal-incidence Bragg mirror. The equations and corresponding graphs of the depths of penetration of hard X-rays in single-crystal are presented in [30] . Also, the energy distribution of the primary beam along the crystal entrance surface is, at least, two orders of magnitude smaller in the case of grazing-incidence diffraction than the energy distribution for the same primary beam in the case of normal-incidence Bragg reflectors. These two circumstances clearly satisfy the requirement of keeping the crystal temperature precisely at a predefined level.

2.1. Coplanar Grazing-Incidence X-Ray Backscattering Diffraction (GIXB)

First, let’s consider the following two reflection schemes from a variety of wave reflectivity models. The fist scheme is a conventional reflection scheme of the plane electromagnetic wave from planar mirror (see Figure 1). According to Figure 1, the equation 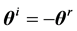holds, where the angles 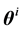and 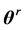are the angles of incidence and reflectance, respectively. The wave vectors of incident 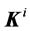and reflected 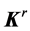beams lie in this figure on the different sides of the normal line to the interface between two media. The vectors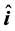, 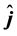and 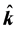are unit vectors along positive directions of Ox-, Oy-, and Oz-axis, respectively.

The second scheme is a retro-reflection scheme of the plane electromagnetic wave (see Figure 2). According to Figure 2, the equation holds, where the angles and are the angles of incidence and retro-reflectance, respectively. The wave vectors of the incident and retro-reflected beams lie on the same side of the normal line to the interface between two media. These two reflection schemes presented in Figure 1 and Figure 2 are indistinguishable in the case of normal incidence when.

One may note that the coplanar geometry of the grazing-incidence hard X-ray backscattering diffraction (GIXB, see the scheme in Figure 3 and translations [30] [31] of our original papers) contains both coplanar reflection schemes presented in Figure 1 and Figure 2. The GIXB technique is a dynamical Bragg diffraction, which holds under

Figure 1. A scheme of conventional reflection from planar mirror.

Figure 2. A scheme of grazing-incidence retro-reflection from planar mirror.

Figure 3. A scheme of coplanar grazing-incidence hard X-ray backscattering diffraction (GIXB) by the diffracting single-crystal wafer., and are the angles of incidence, reflectance and retro-reflectance, respectively. is the reciprocal space vector of diffracting lattice planes (hkl). See text in subsection 2.1 for more details and explanation.

the conditions of total external reflection, and is extremely sensitive to variations of the spacing period of diffracting lattice planes, as well as to variations of the wavelength of incident X-radiation and the angle of incidence of the primary beam. Paper [32] contains the review of the theory and applications of GIXB technique in non-coplanar mode. Particularly, the specular beam suppression and enhancement phenomena are investigated in [32] for the case of non-coplanar GIXB by the crystal with a stacking fault.

The plane presented in Figure 3 is the X-ray entrance surface of the single-crystal wafer. Ox-axis is normal and Oy-axis is parallel to sample diffracting lattice planes. The GIXB setup performs when the magnitude of Bragg angle is close to 90˚, which leads to fulfillment of the following condition, where is a reciprocal lattice vector normal to real space diffracting lattice planes, as it is shown in Figure 3. The reciprocal space vector satisfies the orthogonality conditions:, where and are the unit vectors along the positive direction of Oy-axis and Oz-axis, respectively, is a spacing of the diffracting lattice planes of wafer, which are normal to the X-ray entrance surface. Let and are the angles of the wafer rotation around Oy and Oz coordinate axes, respectively:

, (1)

, (2)

, (3)

where is the first-order kinematic Bragg angle, and is a unit vector along the positive directions of Ox-axis. If the exact condition of coplanar GIXB hold for region, and the angle of incidence of X-ray beam satisfies the first-order Bragg diffraction by lattice planes, then

, (4a)

(4b)

Equation (4b) is the exact condition for the particular case of coplanar GIXB setup derived from general GIXB equations [29] [30] . In this case, the angle of incidence, at which proposed planar mirror reflects X-rays in reverse way, is close to right angle, unlike the homogeneous planar optical mirror, which does this only if the mirror is exactly perpendicular to the wave front, having a zero angle of incidence. The vector presented in Figure 3 is the wave vector of the incident X-ray beam, and the vectors and are the wave vectors of vacuum retro-reflected wave and specular (conventional reflected) wave, respectively. In this coplanar diffraction case the reciprocal space vector, as well as the vacuum wave vectors, , and, lie in the same plane which is parallel to x0z plane. The wave vector makes an angle with wave vector (see Figure 3). Consequently, there are no travelling waves along Oy-axis, so the mentioned wave vectors satisfy the following equations:

, (5)

where

, (6)

and are the wave number and frequency of the incident plane wave, respectively, and c is the speed of light in vacuum.

2.2. Grazing-Incidence Hard X-Ray Retro-Reflector (GIRR)

Now, let’s clarify the performance criteria of the planar grazing-angle incidence hard X-ray retro-reflector (GIRR):

1) A grazing-incidence planar retro-reflector is a mirror with a plane surface that totally reflects (or diffracts) the electromagnetic wave back to its source, and, consequently, the conventional mirror wave is completely suppressed (that is the reflectivity coefficient of conventional mirror wave is equal to zero, see Figure 2).

2) The wave vectors of incident and retro-reflected (or backward diffracted) waves are strictly collinear (see Figure 2).

Therefore, all the types of non-coplanar grazing-incidence hard X-ray diffraction geometries (for example, see [32] ) are not applicable for the GIRR since they do not satisfy the requirement 2). Fortunately, it is possible to transform the coplanar GIXB scheme given in Figure 3 into the required GIRR scheme as given in Figure 2.

・ Thus, the main goal of presented theoretical research is the elaboration and estimation of certain physical and technical solutions that can help to completely suppress a conventional mirror wave and, as a consequence, to increase the retro-ref- lectivity coefficient of the wave with wave vector (see Figure 3).

We propose a solution to this problem through the coplanar GIXB that holds in a single-crystal wafer covered by an ultra-thin, non-diffracting layer of low-absorbing material (see Figure 4). The total retro-reflection can be achieved by ensuring that the

Figure 4. A scheme of coplanar grazing-incidence hard X-ray backscattering diffraction (GIXB) by the diffracting single-crystal wafer covered with an ultra-thin non-diffracting layer of low-absorbing material., and are the angles of incidence, reflectance and retro-reflectance, respectively. is the reciprocal space vector of diffracting lattice planes (hkl). See text in subsections 2.1 and 2.2 for more details and explanation.

intensity of conventional mirror wave is reduced by destructive interference between the wave reflected from wafer and the wave reflected from cover layer. A scheme of proposed GIRR is presented in Figure 4, where the plane is the interface between single-crystal wafer and thin non-diffracting cover layer of thickness, so the plane is the X-ray entrance surface. The other parameters, angles, and vectors are the same as in Figure 3 (see text in subsection 2.1 for the details).

In a particular case of the specular beam suppression mode [32] [33] , the scheme of coplanar grazing-incidence X-ray backscattering diffraction (GIXB) presented in Figure 4 corresponds to total retro-reflection.

The mentioned above grazing-incidence retro-reflection from the proposed planar X-ray optical device is an X-ray analogue of the reflection phenomenon when a light beam is propagating in a photonic crystal, and is incident upon the plane interfaces between the crystal and a uniform dielectric [34] . The authors of paper [34] showed that neither the phase velocity nor the group velocity directions of reflected beam satisfies Snell’s law. The system exhibits remarkable and unusual reflection effects. In particular, total internal reflection is absent except at discrete angular values. The direction of the reflected beam can also be pinned along special crystal directions, independent of the orientation of the interface. At grazing incidences, strong backward reflection occurs (see figure 4 in [34] ). These effects may be important for creating integrated photonic circuits, and for on-chip image transfer [34] .

3. Stationary X-Ray Wave Fields in the Vacuum

All vacuum waves are traveling in the space region, and the angle of incidence of primary X-ray beam satisfies the condition of first-order Bragg diffraction by diffracting lattice planes. In the coplanar diffraction geometry (see Condition (5) and Figure 4), the stationary components of electromagnetic field strength vector of the incident X-ray plane wave are given by the following equations:

, (7a)

(7b)

where is the amplitude of the incident wave field strength. is equal to either or, where corresponds to electric field strength vector of the s-polarized incident X-ray wave field, corresponds to magnetic field strength vector of the p-polarized incident X-ray wave field.

We seek a non-trivial y-component of the stationary X-ray wave field strength vector in vacuum () in the following Fourier integral form:

, (8a)

, (8b)

where is the unknown weight function.

4. Stationary X-Ray Wave Fields inside GIRR

The considered model of GIRR extends over the volume, and for this region we use the following set of well-known stationary material equations:

, (9a)

, (9b)

, (10a)

, (10b)

where is the electric displacement, is the electric field vector, is the dielectric constant of the vacuum, is the magnetic induction, is the magnetic field vector, and is the magnetic permeability of the vacuum. The constants and are related with the speed of light in vacuum c and wave number K via:

, (11)

. (12)

In general, dielectric permittivity, electric susceptibility (polarizability), magnetic permeability, and magnetic susceptibility depend on the position vector. The polarizability is negative for the X-ray wavelengths, and the permeability is also negative for diamagnetic materials. We omit in further calculations since, on average it is at least an order of magnitude smaller than for the same diamagnetic material.

4.1. Solution of the Problem Using a Method of Finding the Eigenvalues and Eigenfunctions

The study of wave propagation in one-dimensional periodic media was pioneered by G. Floquet in 1883 [35] . This theory was extended for three-dimensional periodic media by F. Bloch in 1928 [36] . Bloch proved that waves in such a medium can propagate without scattering, their behaviour governed by a periodic envelope function multiplied by a plane wave.

The same technique can be applied to electromagnetism by considering Maxwell’s equations as an eigenvalues and eigenfuctions problem by analogue with Schrödinger’s equation (see [30] - [33] ). Using such approach, we treat the dynamical diffraction of X-rays by a set of diffracting lattice planes of perfect crystal as the superposition of X-ray “Bloch waves” in a medium with harmonically varying dielectric susceptibility (polarizability). Therefore, the problem of X-ray wave field propagation through an arbitrary set of diffracting lattice planes of periodic structure with the symmetry centre can be brought mathematically to an analogous problem of the solution of stationary Schrödinger equation with cosine-like coefficient [30] . Our method is based on eigenvalues and eigenfunctions problem solution technique. This technique is applicable for both media―the cover layer and crystalline wafer. The common hard X-ray dynamical diffraction theories [10] - [13] did not use this advanced technique. We transform the Maxwell’s equations to the set of differential equations [30] involving the Mathieu or Hill equations [37] - [39] .

4.2. Stationary X-Ray Wave Fields inside Non-Diffracting Cover Layer

We seek a non-trivial y-component of the stationary X-ray wave field strength inside thin non-diffracting cover layer in the following Fourier integral form:

, (13a)

(13b)

where

, (14)

is equal to either or, where corresponds to the electric field strength vector of the s-polarized X-ray wave field inside a thin non-diffracting cover layer, corresponds to the magnetic field strength vector of the p-polarized X-ray wave field inside a thin non-diffracting cover layer. are the unknown weight functions. is the value of polarizability averaged throughout cover layer.

4.3. Stationary X-Ray Wave Fields inside the Single-Crystal Wafer

If absorption is not taken into account, and crystalline wafer has a center of symmetry, then the following relations describe components of the stationary X-ray wave fields inside the crystalline wafer [29] [30] :

, (15a)

(15b)

where

, (16)

, (17)

, (18)

, (19)

, (20)

, (21)

is the real part of the crystal polarizability averaged throughout the crystal lattice cell, is the real part of the Fourier coefficient of the crystal polarizability corresponding to a set of diffracting lattice planes. Functions and are the ordinary Mathieu functions of first kind to which eigenvalues correspond [35] - [37] . and are the unknown weight functions which have to be determined from boundary conditions.

5. Boundary Conditions and Extension of Results for the Absorbing Media

We do not make any assumptions about the X-ray wave field strengths, and with the exception of the requirement that the y-compo- nents of the wave fields (7b), (8b), (13b) and (15b) must satisfy the following boundary conditions:

, (22a)

, (22b)

, (22c)

. (22d)

Using the orthogonality conditions of the functions involved in Equations (7b), (8b), (13b) and (15b), the unknown weight functions, , and, which satisfy the boundary conditions (22a-d), can now be determined. One obtains the required expressions of reflected and transmitted wave fields by the corresponding substitution of the obtained weight functions into Equations (7b), (8b), (13b) and (15b).

In our calculation, the absorption is taken into account by the following substitutions made in the obtained results:

, (23a)

, (23b)

, (23c)

where, and are the real values that describe a wave field energy loss through inelastic interactions of X-rays with atoms and molecules of the retro-reflector [10] - [13] .

6. The Advanced Technologies That Can Be Used for Manufacturing of Hard X-Ray GIRRs

This paper further considers a total retro-reflection of grazing incident hard X-rays from a germanium wafer covered by a thin beryllium layer.

6.1. Choice of Germanium as a Diffracting Substrate for GIRR

The choice of germanium single-crystal wafer for use in GIRR is stipulated by the following reason:

・ Germanium has relatively low melting point and was the first material that could be grown dislocation free. With the improvement of crystal growth, dislocation-free wafers became available and are nowadays the standard in the case of 200 and 400 mm diameter germanium and silicon substrates [40] - [43] .

6.2. Selection of Beryllium as a Cover Layer Material for GIRR

The selection of beryllium as a base material for non-diffracting cover layer is stipulated by the following:

・ Beryllium is a metal that has low density and low atomic mass, and hence very low absorption level of X-rays, making beryllium the preferred choice for X-ray tube windows where the energy low absorption is desired.

・ The surface of beryllium metal, like the aluminum, is covered by a thin layer of oxide that helps protect the metal from attack by acids. Due to this coating, corrosion and oxidation in air is minimal up to temperatures of about 760˚C. Beryllium metal does not react with water or steam, even if the metal is heated to red heat.

6.3. A Technique for Deposition of Thin Metallic Layers on Semiconductors

The deposition of the beryllium thin layer can, for example, be realized via Atomic Layer Deposition (ALD) technology:

・ ALD technology allows semiconductor manufacturers to choose from a wide field of deposition precursors for the application of any thin film in use today on the surface of a large wafer with atomic layer precision.

・ ALD technology can also be used to construct complex, compound film structures with a level of control and conformity that was previously unavailable or impractical.

・ ALD offers the opportunity to create precisely controlled ultra-thin films coating up to 300 mm diameter single-crystal wafers.

・ General ALD process benefits are the excellent process control with wafer-to-wafer repeatability with accuracy less than ±1%, up to 300 mm diameter wafer with typical uniformity accuracy less than ±2%, excellent step coverage even inside high aspect ratio structures, low film impurities, etc. (for example, see [44] ).

6.4. The Thermal Annealing of GIRR

The improvement of tensile strain, crystal quality, and surface morphology of germanium wafer after its covering with thin beryllium layer can be achieved by the thermal annealing. For example, the tensile strain and crystal surface quality, of 500 nm thick Ge films were improved after rapid thermal annealing at 900˚C for a short period less than 20 s [45] . The films were grown on Si(001) substrates by ultra-high vacuum chemical vapour deposition. These improvements are attributed to relaxation and defect annihilation in the Ge films. However, after prolonged more than 20 s rapid thermal annealing, tensile strain and crystal quality degenerated. This phenomenon results from intensive Si-Ge mixing at high temperature.

The solid solubility of beryllium in germanium is extremely small up to temperatures of about 900˚C, and, consequently, the mutual diffusion process of atoms between germanium wafer and beryllium layer has very low rate (see Fig. 15.11 in [46] ).

・ This type of properties opens the opportunity of removing the interface tensile strain and improving the crystal quality and morphology of subsurface region of germanium wafer covered by thin beryllium layer through the application of a longer thermal annealing method at, for example, 700˚C practically without any appreciable inter-diffusion between these two materials. The essential reduction of the tensile strain along the Be-Ge large interface will increase the survivability of the coverage layer.

6.5. The Array of GIRRs

The main problem of experimental research involving the grazing-incidence hard X-ray optics is the small collection efficiency due to the small critical angle, since the collection area of grazing incidence mirrors is the projection of the mirror surface onto the aperture plane.

A Japanese optics company, JTEC Corporation, fabricates the mirrors for synchrotrons and other X-ray laser research facilities [47] such as Japan’s Spring-8 Angstrom Compact Free-Electron Laser (SACLA) and the European X-ray Free-Electron Laser (EXFEL), located in Hamburg, Germany and due to come online in 2017. Recently, scientists installed new mirrors to improve the quality of the X-ray laser beam at the Department of Energy’s SLAC National Accelerator Laboratory. The meter-long mirrors are the ultimate in flatness, smooth to within the height of one atom or one-fifthof a nanometer [48] . Each mirror is made from an individual silicon crystal, artificially grown in a lab. After the mirror is polished with conventional techniques, the company uses a process called elastic emission machining, where a jet of ultra-pure water containing fine particles removes any remaining imperfections atom by atom. The same advanced technology may be used for the GIRR manufacturing.

An alternative method to long plane retro-reflectors is a nesting multiple GIRRs that also increases the collection area, and a thin metallic coating will further increase the critical angle and thus collection efficiency (see Figure 5).

7. The Discussion of GIRR Reflectivity Coefficients

We analyze below the solutions for vacuum stationary hard X-ray wave fields for the optimization of system design parameters and diffraction conditions that satisfy well the performance objectives of GIRR (see subsection 2.2).

Figure 5. A cascade of GIRRs. The extra-large-area retro-reflector is prepared using an array (or a mosaic) of individual large single-crystal wafers. Special processing techniques maintain the orientation of the individual crystals to very high accuracy. The angles and are the angles of incidence and retro-reflectance of the plane X-ray wave field, and the wave vectors of the incident and retro-reflected beams lie on the same side of the normal line in respect to the interface between the two media.

7.1. GIXB by Bulk Germanium Wafer without Cover Layer

Let’s discuss a diffraction in case where the exact condition of coplanar GIXB holds inside bulk germanium wafer without cover layer, and the angle of incidence of X-ray primary beam satisfies the first-order Bragg diffraction by the lattice planes:

, (24)

. (25)

The reflectivity coefficients from a single-crystal wafer and visibility of images obtained from subsurface non-diffracting regions of wafer are described by the following formulas:

, (26)

, (27)

where n = 0, 1, 2, the function is the X-ray reflectivity coefficient of a single-crystal wafer without a cover layer in the case when the Bragg condition is not satisfied, the functions and are the retro-reflectivity and reflectivity coefficients, respectively [30] [31] . The graphs of reflectivity coefficients and visibility of images depending on Bragg angle are presented in Figure 6.

These graphs are computed using the values of the incidence angle taken from the angular region presented below:

Figure 6. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle while the coplanar GIXB by lattice planes (422) holds inside bulk germanium single-crystal wafer without a cover layer. The diffracting lattice planes (422) are normal to X-ray entrance plane surface.

. (28a)

Equation (28a) can be rewritten in the following form using Equation (3):

, (28b)

where, is the germanium lattice constant at the room temperature, and [49] [50] .

The polarizability Fourier components, , , and are calculated based on the method of computer simulation of experimental results for the complex kinematic scattering parameters of X-rays [51] . The maximum value of the retro-reflectivity coefficient corresponds to , and the visibility function (see Figure 6). Also, note that, so the mirror wave field reflected from crystal wafer does not get completely suppressed.

7.2. GIXB by Bulk Germanium Wafer Covered with Beryllium Layer

One may write the following relation between and polarization modes of electric wave field propagating inside the crystalline wafer [10] - [13] :

. (29)

Since GIXB setup performs only if the magnitude of Bragg angle is close to 90˚, then the square of polarization factor, and, according to (29), the intensities of X-ray wave fields inside the crystalline wafer are practically the same for both and polarization modes.

The diffraction angles can be determined through the system of analyzer crystals with an accuracy of at least, and can be obtained experimentally under the conditions of high diffraction intensity in grazing-angle incidence geometry, notwithstanding the fact that the cap layer thickness is less than 5 nm [52] . Therefore, the presence of a thin cap layer may essentially change the reflectivity properties of single- crystal substrate when the GIXB holds inside.

Here we analyze a particular case of coplanar GIXB by germanium single-crystal wafer covered with thin non-diffracting beryllium layer. Our goal is to find an opportunity to reduce the common reflected wave and increase the retro-reflected one.

The graphs of X-ray reflectivity coefficients, , as well as the retro-reflectivity coefficient and visibility function, are presented in Figure 7. These graphs depend on the thickness T of beryllium cap layer while the coplanar GIXB by lattice planes holds inside bulk germanium single-crystal wafer for the particular case of kinematic Bragg angle.

Figure 7. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle while the coplanar GIXB by lattice planes (422) holds inside bulk germanium single-crystal wafer without a cover layer. The diffracting lattice planes (422) are normal to X-ray entrance plane surface.

Curves in Figure 7 correspond to the incident X-ray wavelength and to absolute values of the electric susceptibility coefficients for beryllium layer and germanium wafer presented below:

, ,

, ,

,.

The coefficients, , , and visibility are oscillating functions with slowly damping amplitude (see Figure 7). Coefficients and have the same period and are mutually shifted for a half of a period. The zeros of reflectivity coefficient correspond to certain values of cover layer thicknesses, where, ,. In this particular case when, the identity holds because a complete suppression of the reflectivity coefficient in the direction of conventional mirror wave happens due to destructive interference between the X-ray wave reflected from crystal wafer and X-ray wave reflected from the cover layer. Also, in this particular case, the retro-reflectivity coefficient has local maximums, and visibility function is . It can be noted that the following approximate relations hold for the neighbour extremal values since these coefficients have the slowly damping amplitudes:

(30)

The relation (30) can be rewritten in the following form:

(31)

Hence, a small changes of the cover layer thickness equal to leads to essential redistribution in magnitudes of reflectivity and retro-reflectivity coefficients. Fortunately, the advanced nano-technologies of the present day allow the layer deposition and the thickness control with less than 1 nm accuracy. The magnitudes of local maximums of the retro-reflectivity coefficient are greater than the magnitudes of the neighbour local maximums of reflectivity coefficients .

The comparison of the corresponding graphs presented in Figure 6 and Figure 7 brings to the following relations:

, (32a)

, (32b)

(32c)

. (32d)

The relation (32c) can be rewritten in the following form:

, (33)

where j = 0, 1 (see Figure 7). The enhancement of retro-reflectivity coefficient of a single crystal wafer happens if it has a thin non-diffracting cover layer (see Equation (33)). This phenomenon is caused by the constructive interference between the X-ray wave field retro-reflected from crystal wafer and the X-ray waves multiply reflected from the top and bottom surfaces of the cover layer.

Now, let’s consider the X-ray reflectivity and retro-reflectivity coefficients and visibility function depending on the Bragg angle. In this particular case, the coplanar GIXB by lattice planes holds inside bulk germanium wafer covered with a thin non-diffracting beryllium layer of thickness. The corresponding graphs are presented in Figure 8. It can be noted from Figure 8 that the extreme values

Figure 8. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle while the coplanar GIXB by lattice planes (422) holds inside bulk germanium crystalline wafer covered with non-diffracting beryllium layer with the thickness T = 30 nm. The diffracting lattice planes (422) are normal to X-ray entrance plane surface.

of the reflectivity graphs, , as well as of the visibility function graph correspond to the magnitude of Bragg angle.

We present below three-dimensional graphs of the retro-reflectivity and reflectivity coefficients, as well as the visibility function depending on both variables and T (see Figures 9-12). According to the graphs presented in Figures 9-12, the following limit equations hold:

Figure 9. The retro-reflectivity coefficient.

Figure 10. The reflectivity coefficient.

Figure 11. The reflectivity coefficient if the Bragg condition is not satisfied.

Figure 12. The graph of visibility function.

, (34a)

, (34b)

where T is an arbitrary value of the cover layer thickness. Note that the maximums on oscillating graphs of reflectivity and retro-reflectivity coefficients and of visibility function correspond to kinematic Bragg angle (see Figures 9-12).

7.3. Hard X-Ray Optical Noise and Background Filter

The modern laboratory X-ray source has a high intensity X-ray beam close to 10⁹ photons s⁻¹ focused on the sample surface by using a Cu rotating anode X-ray generator operated at 40 kV - 30 mA (1.2 kW), according to paper [52] . The design, implementation, and performance of an X-ray monochromator with ultra-high energy resolution of at 14.41 keV is given in [53] .

The images of non-diffracting nano-sized subsurface inclusions, obtained by the hard X-rays scattering process, show a high-intensity background, so, besides a sufficient intensity and energy resolution, the advanced hard X-ray image registration system needs an all-optical filter that removes unwanted background or optical noise from the conventional specular wave and essentially increases the visibility of the informative signal.

In the retro-reflection performance mode, a planar GIRR removes the primary radiation from the common reflected beam propagating in the direction of the wave vector (see Figure 4). Consequently, using the proposed experimental scheme, researchers will be able to register weak signals scattered by non-diffracting inclusions located at wafer’s subsurface region (if there are any).

Finally, we can conclude that single crystal wafer covered by a thin cover layer with a certain thickness performs like an X-ray optical noise (or background) filter. Moreover, simultaneously with the increase in the magnitude of the visibility function, a diminishing of certain effects occurs, for example, in the probability of data read-out errors and data read-out time during the digital data read-out procedure from X-ray optical data carrier preliminary covered by a thin non-diffracting protective layer [33] .

8. Conclusions

・ Proposed grazing-incidence retro-reflector (GIRR) is a plane mirror that totally reflects (or diffracts) the grazing-incidence hard X-ray photons back to its source.

・ The planar GIRR (or a cascade of GIRRs, see the subsection 6.5) consists of single-crystal wafer(s) covered by an ultra-thin, non-diffracting layer of low-absorbing material, and can be applied in hard X-ray optical noise (or background) filters, high-quality hard X-ray waveguides, low-gain hard X-ray free electron laser resonators (XFELRs), X-ray holography, coherent X-ray diffraction imaging, phase-con- trast imaging, as well as in hard X-ray optical data storage devices [32] [33] and deep space hard X-ray communications [6] - [9] .

・ The authors justify in Section 6 of this paper the selection of a germanium and beryllium material for the design of planar GIRR, as well as review the advanced nano-technologies of the present day through which the GIRR can be implemented.

・ Changes in thickness of cover layer bring to oscillations with slowly damping (relative to oscillations period) amplitude of the hard X-ray reflectivity and retro-reflec- tivity coefficients, as well as of the visibility function (see Figure 7 and Figures 9-12).

・ From the analysis of graphs presented in Figures 7-12, the authors conclude that the coplanar GIXB at a certain value of the Bragg angle by lattice planes (422) of germanium single-crystal wafer covered by the beryllium non-dif- fracting layer with a thickness (where, , , see the GIXB scheme presented in Figure 4) satisfies the both performance criteria 1) and 2) for the planar GIRR defined in subsection 2.2.

・ The authors overcome a thermal expansion problem due to GIXB scheme, since the X-ray penetration depths in crystal wafer are at least in three orders smaller than in diffraction methods, which rely on normal-incidence Bragg reflectors. Also, the energy distribution of the primary beam along the crystal entrance surface is, at least, two orders of magnitude smaller in the case of grazing-incidence diffraction than the energy distribution for the same primary beam in the case of normal-incidence Bragg reflectors. These two circumstances clearly satisfy the requirement of keeping the crystal temperature precisely at a predefined level.

*The paper is devoted to memory of Prof. Dr. Petros Bezirganyan (1916-1994). Towards the 100th Anniversary of his birthday on 15th December 2016.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Akiyama, T., Yoshida, N., Kawahata, K., Tokitani, M., Iwakiri, H., Okajima, S. and Nakayama, K. (2012) Studies of Reflectivity Degradation of Retroreflectors in LHD and Mitigation of Impurity Deposition Using Shaped Diagnostic Ducts and Protective Windows. Nuclear Fusion, 52, Article ID: 063014. http://dx.doi.org/10.1088/0029-5515/52/6/063014
[2]	Schultz, P., Cumby, B. and Heikenfeld, J. (2012) Investigation of Five Types of Switchable Retroreflector Films for Enhanced Visible and Infrared Conspicuity Applications. Applied Optics, 51, 3744-3754. http://dx.doi.org/10.1364/AO.51.003744
[3]	Ooi, C.H.R. (2010) Superintense Laser Fields from Multiple Laser Pulses Retro-Reflected in Circular Geometry. Journal of Applied Physics, 107, Article ID: 043110. http://dx.doi.org/10.1063/1.3296128
[4]	Groswasser, D., Waxman, A., Givon, M., Aviv, G., Japha, Y., Keil, M. and Folman, R. (2009) Retroreflecting Polarization Spectroscopy Enabling Miniaturization. Review of Scientific Instruments, 80, Article ID: 093103. http://dx.doi.org/10.1063/1.3213076
[5]	Dell’Agnello, S., Delle Monache, G., Vittori, R., Boni, A., Cantone, C., Ciocci, E., Martini, M., Patrizi, G., Tibuzzi, M., Bianco, G., Currie, D., Intaglietta, N., Salvatori, L., Lops, C., Contessa, S., Porcelli, L., Mondaini, C., Tuscano, P. and Maiello, M. (2015) Advanced Laser Retroreflectors for Astrophysics and Space Science. Journal of Applied Mathematics and Physics, 3, 218-227. http://dx.doi.org/10.4236/jamp.2015.32032
[6]	Hemmati, H., Ed. (2006) Deep Space Optical Communications. JPL Deep Space Communications and Navigation Series. John Wiley & Sons Inc., Hoboken. http://www.wiley.com/WileyCDA/WileyTitle/productCd-0470040025.html
[7]	Arnon, S., Barry, J., Karagiannidis, G., Schober, R. and Uysaleds, M., Eds. (2012) Advanced Optical Wireless Communication Systems. Cambridge University Press, Cambridge. http://www.cambridge.org/9780521197878
[8]	Ghassemlooy, Z., Popoola, W.P. and Rajbhandari, S. (2013) Optical Wireless Communications: System and Channel Modelling with Matlab. CRC Press, Boca Raton. https://www.crcpress.com/Optical-Wireless-Communications-System-and-Channel- Modelling-with-MATLAB/Ghassemlooy-Popoola-Rajbhandari/p/book/9781439851883
[9]	Arnon, S. (Ed.) (2015) Visible Light Communication. Cambridge University Press, Cambridge. http://www.cambridge.org/us/academic/subjects/engineering/communications-and-signal- processing/visible-light-communication?format=HB
[10]	James, R.W. (1967) The Optical Principles of the Diffraction of X-Rays. Cornel University Press, Ithaca.
[11]	Azaroff, L.V., Kap-low, R., Kato, N., Weiss, R.J., Wilson, A.J.C. and Young, R.A. (1974) X-Ray Diffraction. In: Farnsworth, J.L. and Bradley, J.W., Eds., International Series in Pure and Applied Physics, McGraw-Hill Pub. Co., New York, 664 p.
[12]	Pinsker, Z.G. (1978) Dynamical Scattering of X-Rays in Crystals. Springer-Verlag, Berlin. http://www.springer.com/us/book/9783642812095
[13]	Authier, A. (2001) Dynamical Theory of X-Ray Diffraction. Oxford University Press, Oxford. https://global.oup.com/academic/product/dynamical-theory-of-X-ray-diffraction- 9780198528920?lang=en&cc=us
[14]	Kohra, K. and Matsushita, T. (1972) Some Characteristics of Dynamical Diffraction at a Bragg Angle of about π/2. Zeitschrift für Naturforschung, 27, 484-487. http://zfn.mpdl.mpg.de/data/Reihe_A/27/ZNA-1972-27a-0484.pdf http://dx.doi.org/10.1515/zna-1972-0317
[15]	Brümmer, O., Höche, H.R. and Nieber, J. (1979) X-Ray Diffraction in the Bragg Case at Bragg Angles of about π/2. Physica Status Solidi (A), 53, 565-570. http://dx.doi.org/10.1002/pssa.2210530220
[16]	Graeff, W. and Materlik, G. (1982) Millielectron Volt Energy Resolution in Bragg Backscattering. Nuclear Instruments and Methods in Physics Research, 195, 97-103. http://dx.doi.org/10.1016/0029-554X(82)90764-9
[17]	Caticha, A. and Caticha-Ellis, S. (1982) Dynamical Theory of X-Ray Diffraction at Bragg Angles Near π/2. Physical Review B, 25, 971-983. http://dx.doi.org/10.1103/PhysRevB.25.971
[18]	Sutter, J.P., Alp, E.E., Hu, M.Y., Lee, P.L., Sinn, H., Sturhahn, W. and Toellner, T.S. (2001) Multiple-Beam X-Ray Diffraction Near Exact Backscattering in Silicon. Physical Review B, 63, Article ID: 094111. http://dx.doi.org/10.1103/physrevb.63.094111
[19]	Caticha, A., Aliberti, K. and Caticha-Ellis, S. (1996) A Fabry-Perot Interferometer for Sub-meV X-Ray Energy Resolution. Review of Scientific Instruments, 67, 3380-3381. http://dx.doi.org/10.1063/1.1147321
[20]	Liss, K.-D., Hock, R., Gomm, M., Waibel, B., Magerl, A., Krisch, M. and Tucoulou, R. (2001) X-Ray Photon Storage in a Crystal Cavity. In: Mills, D.M., Schulte-Schrepping, H. and Arthur, J.R., Eds., X-Ray FEL Optics and Instrumentation, SPIE Press, Bellingham, 78-88. http://dx.doi.org/10.1117/12.413682
[21]	Chang, S.-L., Stetsko, Y.P., Tang, M.-T., Lee, Y.-R., Sun, W.-H., Yabashi, M. and Ishikawa, T. (2005) X-Ray Resonance in Crystal Cavities: Realization of Fabry-Perot Resonator for Hard X-Rays. Physical Review Letters, 94, Article ID: 174801. http://dx.doi.org/10.1103/physrevlett.94.174801
[22]	Chang, S.-L., Stetsko, Y.P., Tang, M.-T., Lee, Y.-R., Sun, W.-H., Yabashi, M., Ishikawa, T., Wu, H.-H., Shew, B.-Y., Lin, Y.-H., Kuo, T.-T., Tamasaku, K., Miwa, D., Chen, S.-Y., Chang, Y.-Y. and Shy, J.-T. (2006) Crystal Cavity Resonance for Hard X Rays: A Diffraction Experiment. Physical Review B, 74, Article ID: 134111. http://dx.doi.org/10.1103/physrevb.74.134111
[23]	Wu, Y.-H., Tsai, Y.-W., Chu, C.-H., Liu, W.-C., Chang, Y.-Y. and Chang, S.-L. (2015) Inclined-Incidence Hard-X-Ray Resonator with Ultrahigh Efficiency and Resolution. Optics Express, 23, 9994-10001. http://dx.doi.org/10.1364/OE.23.009994
[24]	Tsai, Y.-W., Wu, Y.-H., Chang, Y.-Y., Liu, W.-C., Liu, H.-L., Chu, C.-H., Chen, P.-C., Lin, P.-T., Fu, C.-C. and Chang, S.-L. (2016) Sapphire Hard X-Ray Fabry-Perot Resonators for Synchrotron Experiments. Journal of Synchrotron Radia-tion, 23, 658-664. http://dx.doi.org/10.1107/S1600577516004999
[25]	Caticha, A. and Cati-cha-Ellis, S. (1990) A Fabry-Perot Interferometer for Hard X-Rays. Physica Status Solidi (A), 119, 643-654. http://dx.doi.org/10.1002/pssa.2211190228
[26]	Huang, X.R., Siddons, D.P., Ma-crander, A.T., Peng, R.W. and Wu, X.S. (2012) Multicavity X-Ray Fabry-Perot Resonance with Ultrahigh Resolution and Contrast. Physical Review Letters, 108, Article ID: 224801. http://dx.doi.org/10.1103/physrevlett.108.224801
[27]	Bergamin, A., Cavagnero, G., Mana, G. and Zosi, G. (1999) Scanning X-Ray Interferometry and the Silicon Lattice Parameter: Towards Relative Uncertainty? European Physical Journal B, 9, 225-232. http://dx.doi.org/10.1007/s100510050760
[28]	Ferroglio, L., Mana, G. and Massa, E. (2008) Si Lattice Parameter Measurement by Centimeter X-Ray Interferometry. Optics Express, 16, 16877-16888. http://dx.doi.org/10.1364/OE.16.016877
[29]	Massa, E., Mana, G., Kuetgens, U. and Ferroglio, L. (2011) Measurement of the {2 2 0} Lattice-Plane Spacing of a 28Si X-Ray Interferometer. Metrologia, 48, S37-S43. http://dx.doi.org/10.1088/0026-1394/48/2/S06
[30]	Bezirganyan, H.P. and Bezirganyan, P.H. (1988) Solution of the Two-Dimensional Stationary Schrödinger Equation with Cosine-Like Coefficient (In View of X-Ray Diffraction). Physica Status Solidi (A), 105, 345-355. http://dx.doi.org/10.1002/pssa.2211050205
[31]	Bezirganyan, H.P. (1988) X-Ray Reflection from and Transmission through a Plane-Parallel Dielectric Plate with Cosine-Like Polarizability (Symmetrical Laue Case). Physica Status Solidi (A), 109, 101-110. http://dx.doi.org/10.1002/pssa.2211090109
[32]	Bezirganyan, H.P., Bezirganyan Jr., H.H., Bezirganyan, S.E. and Bezirganyan Jr., P.H. (2004) Specular Beam Suppression and Enhancement Phenomena in the Case of Grazing-Angle Incidence X-Rays Back Diffraction by the Crystal with Stacking Fault. Optics Communications, 238, 13-28. http://dx.doi.org/10.1016/j.optcom.2004.04.038
[33]	Bezirganyan, H.P., Bezirganyan Jr., H.H., Bezirganyan, S.E., Bezirganyan Jr., P.H. and Mossikyan, Y.G. (2005) An Ultrahigh-Density Digital Data Readout Method Based on Grazing-Angle Incidence X-Ray Backscattering Diffraction. Journal of Optics A: Pure and Applied Optics, 7, 604-612. http://dx.doi.org/10.1088/1464-4258/7/10/013
[34]	Yu, X. and Fan, S. (2004) Anomalous reflections at photonic crystal surfaces. Phys. Rev. E, 70, Article ID: 055601. http://dx.doi.org/10.1103/physreve.70.055601
[35]	Floquet, G. (1883) Sur les équations différentielles linéaires à coefficients périodiques. Annales Scientifiques de l’école Normale Supérieure,12, 47-88. http://www.numdam.org/item?id=ASENS_1883_2_12__47_0
[36]	Bloch, F. (1928) über die Quantenmechanik der Elektronen in Kristallgittern. Zeitschrift für Physik, 52, 555-600. http://www.pwein.at/physics/Lectures/Famous-Papers/Z-Physik-52-555-1928.pdf http://dx.doi.org/10.1007/BF01339455
[37]	Mathieu, E. (1868) Memoire sur le Mouvement Vibratoire d’une Membrane de Forme Elliptique. Journal de Mathématiques Pures et Appliquées, 13, 137-203. https://eudml.org/doc/234720
[38]	McLachlan, N.W. (1947) Theory and Application of Mathieu Functions. Oxford University Press, London. https://www.amazon.com/Theory-Application-Mathieu-Functions-McLachlan/dp/ B0007DMXT6
[39]	Meixner, J., Schaefke, F.W. and Wolf, G. (1980) Mathieu Functions and Spheroidal Functions and Their Mathematical Foundations. Springer, Berlin. http://dx.doi.org/10.1007/BFb0096194
[40]	Shiraishi, Y., Takano, K., Matsubara, J., Iida, T., Takase, N., Machida, N., Kuramoto, M. and Yamagishi, H. (2001) Growth of Silicon Crystal with a Diameter of 400 mm and Weight of 400 kg. Journal of Crystal Growth, 229, 17-21. http://dx.doi.org/10.1016/S0022-0248(01)01042-9
[41]	Yamagishi, H., Kuramoto, M., Shiraishi, Y., Machida, N., Takano, K., Takase, N., Iida, T., Matsubara, J., Minami, H., Imai, M. and Takada, K. (1999) Large Diameter Silicon Technology and Epitaxy. Microelectronic Engineering, 45, 101-111. http://dx.doi.org/10.1016/S0167-9317(99)00106-9
[42]	Claeys, C. and Simoen, E. (2009) Extended Defects in Germanium: Fundamental and Technological Aspects. Springer, Berlin, Heidelberg. http://link.springer.com/book/10.1007/978-3-540-85614-6 http://dx.doi.org/10.1007/978-3-540-85614-6
[43]	Tanner, B.K., Wittge, J., Vagovic, P., Baumbach, T., Allen, D., McNally, P.J., Bytheway, R., Jacques, D., Fossati, M.C., Bowen, D.K., Garagorri, J., Elizalde, M.R. and Danilewsky, A.N. (2013) X-Ray Diffraction Imaging for Predictive Metrology of Crack Propagation in 450-mm Diameter Silicon Wafers. Powder Diffraction, 28, 95-99. http://dx.doi.org/10.1017/S0885715613000122
[44]	Van Hemmen, J.L., Heil, S.B.S., Klootwijk, J.H., Roozeboom, F., Hodson, C.J., van de Sanden, M.C.M. and Kessels, W.M.M. (2007) Plasma and Thermal ALD of Al2O3 in a Commercial 200 mm ALD Reactor. Journal of the Electrochemical Society, 154, G165-G169. http://jes.ecsdl.org/content/154/7/G165 http://dx.doi.org/10.1149/1.2737629
[45]	Lu, Z., et al. (2013) Effects of High Temperature Rapid Thermal Annealing on Ge Films Grown on Si(001) Substrate. Chinese Physics B, 22, Article ID: 116804. http://dx.doi.org/10.1088/1674-1056/22/11/116804
[46]	Walsh, K.A. (2009) Beryllium Chemistry and Processing. ASM International, USA, 183. http://www.asminternational.org/search/-/journal_content/56/10192/05223G/PUBLICATION
[47]	JTEC Corporation. Development and Production of Optical Mirrors for Synchrotron Radiation. Japan. http://j-tec.co.jp/english/index.html
[48]	The X-Ray Mirrors That Differ by One Atom in Flatness from End to End. SLAC National Accelerator Laboratory News. https://www6.slac.stanford.edu/news/2016-08-01-perfection-sight-slac-receives-new-mirrors -x-ray-laser.aspx
[49]	Szwacki, N.G. and Szwacka, T. (2015) Basic Elements of Crystallo-graphy. Pan Stanford Publishing Pte. Ltd., Singapore. http://www.panstanford.com/books/9789814613576.html
[50]	Martienssen, W. and Warlimont, H., Eds. (2005) Springer Handbook of Condensed Matter and Materials Data. Springer, Berlin. http://www.springer.com/us/book/9783540304371 http://dx.doi.org/10.1007/3-540-30437-1
[51]	Kohn, V.G. (2006) Program for Calculating the Scattering Parameters Used in the X-Ray Standing Wave Method. Crystallography Reports, 51, 936-940. http://link.springer.com/article/10.1134%2FS1063774506060034 http://dx.doi.org/10.1134/S1063774506060034
[52]	Omote, K. (2010) High Resolution Grazing-Incidence In-Plane X-Ray Diffraction for Measuring the Strain of a Si Thin Layer. Journal of Physics: Condensed Matter, 22, Article ID: 474004. http://dx.doi.org/10.1088/0953-8984/22/47/474004
[53]	Yabashi, M., Tamasaku, K., Kikuta, S. and Ishikawa, T. (2001) X-Ray Monochromator with an Energy Resolution of 8 × 10?9 at 14.41 keV. Review of Scientific Instruments, 72, 4080-4083. http://dx.doi.org/10.1063/1.1406925