Generalized Ratio-Cum-Product Estimators for Two-Phase Sampling Using Multi-Auxiliary Variables

John Kung’u, Joseph Nderitu

Department of Statistics and Actuarial Science, Kenyatta University, Nairobi, Kenya.

DOI: 10.4236/ojs.2016.64052                

Abstract

In this paper, we have proposed estimators of finite population mean using generalized Ratio- cum-product estimator for two-Phase sampling using multi-auxiliary variables under full, partial and no information cases and investigated their finite sample properties. An empirical study is given to compare the performance of the proposed estimators with the existing estimators that utilize auxiliary variable(s) for finite population mean. It has been found that the generalized Ra-tio-cum-product estimator in full information case using multiple auxiliary variables is more efficient than mean per unit, ratio and product estimator using one auxiliary variable, ratio and product estimator using multiple auxiliary variable and ratio-cum-product estimators in both partial and no information case in two phase sampling. A generalized Ratio-cum-product estimator in partial information case is more efficient than Generalized Ratio-cum-product estimator in No information case.

Keywords

Ratio-Cum-Product Estimator, Multiple Auxiliary Variables, Two-Phase Sampling

Received 20 May 2016; accepted 13 August 2016; published 16 August 2016

1. Introduction

The history of using auxiliary information in survey sampling is as old as history of the survey sampling. The work of Neyman [1] may be referred to as the initial works where auxiliary information has been used. Cochran [2] used auxiliary information in single phase sampling to develop the ratio estimator for estimation of population mean. In the ratio estimator, the study variable and the auxiliary variable had a high positive correlation and the regression line was passing through the origin. Hansen and Hurwitz [3] also suggested the use of auxiliary information in selecting the sample with varying probabilities.

Olkin [4] was the first author to deal with the problem of estimating the mean of survey variable when auxiliary variables are made available. He suggested the use of information on more than one auxiliary variable, highly positively correlated with the study variable analogously to Olkin; Murthy’s [5] using product estimator envisaged by Robson [6] used auxiliary information in single phase sampling to develop the product estimator for estimation of population mean. In the product estimator, the study variable and the auxiliary variable had a high negative correlation. Singh [7] gave a multivariate expression of Murthy’s [5] product estimator, while Raj [8] put forward a method for using multi auxiliary variables through a linear combination of single difference estimators. Moreover, Singh [9] considered the extension of the ratio-cum-product estimators to multi-auxiliary variables. John [10] suggested two multivariate generalizations of ratio and product estimators which actually reduce to the Olkin’s [4] and Singh’s [7] estimators. Srivastava [11] proposed a general ratio-type estimator that generates a large class of estimators including most of the estimators up to that time proposed.

The concept of double sampling was first proposed by Neyman [1] in sampling human populations when the mean of auxiliary variable was unknown. It was later extended to multiphase by Robson [12] It is advantageous when the gain in precision is substantial as compared to the increase in the cost due to collection of information on the auxiliary variate for large samples. Ahmad [13] proposed generalized multivariate ratio and regression estimators for multi-phase sampling for estimating population mean.

In this paper, we have extended the Ratio-cum-product estimator suggested by Singh [9] to two phase samplingby considering the three strategies proposed by Samiuddin and Hanif [14] i.e. when either information for all these auxiliary is available from population or available for some auxiliary variables or not available for all auxiliary variables also incorporate Arora and Bansi [15] approach in writing down the mean squared error.

2. Preliminaries

2.1. Notations

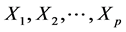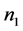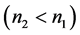
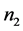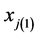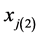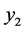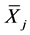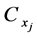Consider a population of N units. Let Y be the study variable for which we want to estimate its population mean and are p auxiliary variables. For two phase sampling design let and be sample sizes for first and second phase respectively. and denote the auxiliary variables form first and second phase samples respectively and denote the variable of interest from second phase. and denote the population means and coefficient of variation of 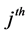auxiliary variables respectively and 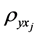denotes the population correlation coefficient of Y and.

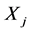Further, let, ,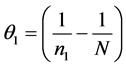

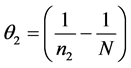, and, (1.0)

where, and are sampling error and are very small. We assume that,

. (1.1)

The coefficient of variation and correlation are given by,

, and then for simple random sampling without replacement

for both first and second phases we write by using phase wise operation of expectations as:

,

,

,

(1.2)

Let the so, hence

Also, then (1.3)

We shall take to term of order as

(1.4)

(1.5)

Arora and Lai [15] (1.6)

The following notations will be used in deriving the mean square errors of proposed estimators

Determinant of population correlation matrix of variables

Determinant of minor of corresponding to the element of

Denotes the multiple coefficient of determination of y on.

Denotes the multiple coefficient of determination of y on.

Determinant of population correlation matrix of variables.

Determinant of population correlation matrix of variables

Determinant of the correlation matrix of.

Determinant of the correlation matrix of.

Determinant of the minor corresponding to of the correlation matrix of

.

Determinant of the minor corresponding to of the correlation matrix of

(1.7)

2.2. Mean per Unit in Two Phase Sampling

The sample mean using simple random sampling without replacement is given by,

(2.0)

While its variance is given,

(2.1)

2.3. Ratio Estimator Using Auxiliary Variable in Two Phase Sampling

The ratio estimator when information on one auxiliary variables is available form the population (Full information Case) is:

(2.2)

where and the mean square error can be written as:

(2.3)

2.4. Product Estimator Using Auxiliary Variable in Two Phase Sampling

The product estimator when information on one auxiliary variables is available for population (Full information Case) is:

(2.4)

where and the mean square error can be written as:

(2.5)

2.5. Ratio Estimator Using Multi-Auxiliary Variables in Two Phase Sampling

The Ratio estimator suggested by Ahmad [13] when information on both auxiliary variables is available for population (Full information Case) is:

(2.6)

The optimum values of unknown constants are

(2.7)

and mean square can be written as:

(2.8)

2.6. Product Estimator Using Multi-Auxiliary Variable in Two Phase Sampling

The product estimator suggested when information on both auxiliary variables is available for population (Full information Case) is:

(2.9)

The optimum values of unknown constants are

(2.10)

and mean square can be written as:

(2.11)

In general these estimators have a bias of order. Since the standard error of the estimates is of order, the quantity bias/s.e is of order and becomes negligible as n becomes large. In practice, this quantity is

usually unimportant in samples of moderate and large sizes.

In this paper, we have extended the Ratio-cum-product estimator suggested by Singh [9] to two phase sampling by considering the three strategies proposed by Samiuddin and Hanif [14] i.e. when either information for all these auxiliary is available from population or available for some auxiliary variables or not available for all auxiliary variables also incorporate Arora and Bansi [15] approach in writing down the mean squared error.

3. Methodology

3.1. Proposed Ratio-Cum-Product Estimator in Two Phase Sampling (Full Information Case)

If we estimate a study variable when information on all auxiliary variables is available from population, it is utilized in the form of their means. By taking the advantage of Ratio-cum-Producttechnique for two-phase sampling, a generalized estimator for estimating population mean of study variable Y with the use of multi auxiliary variables is suggested as:

(3.0)

Substituting Equation (1.0) in (3.0), we get,

(3.1)

Using (1.3) in (3.1) and ignoring the second and higher terms for each expansion of product and after simplification we can write as,

(3.2)

The mean squared error of is given by,

(3.3)

We differentiate the Equation (3.3) partially with respect to and then equate to zero, using (1.5) and (1.7), we get.

(3.4)

(3.5)

Using normal equation that is used to find the optimum values given (3.3) we can write,

(3.6)

Taking expectation of (3.6) we get,

(3.7)

Using (1.2) in (3.7) and simplifying, we get,

(3.8)

Substituting (3.4) and (3.5) in (3.8), we get,

(3.9)

Or

(3.10)

Or

(3.11)

Or

(3.12)

Using (1.6) in (3.12), we get

(3.13)

3.2. Ratio-Cum-Product Estimator in Two Phase Sampling (Partial Information Case)

In this case suppose we have no information on all s and t auxiliary variables but only for r and g auxiliary varia- bles from population. Considering Ratio-Cum-Product technique of estimating technique, the population mean of study variable Y can be estimated for two-phase sampling using multi-auxiliary variables is suggested as:

(3.14)

Simplifying (3.14) we get,

(3.15)

Using (1.0), (1.3) and (1.4) in (3.15) and ignoring the second and higher terms for each expansion of product and after simplification we can write as,

(3.16)

Mean squared error of estimator is given by

(3.17)

We differentiate the Equation (3.17) with respect to and equate to zero and use (1.6) and (1.7). The optimum values are as follows,

(3.18)

Using normal equation that is used to find the optimum values given (3.18) we can write.

(3.19)

Or

(3.20)

Using (1.2) in (3.20) we get,

(3.21)

Substituting (3.18) to (3.22) we get,

(3.22)

Or

(3.23)

Or

(3.24)

Or

(3.25)

Using (1.6) in (3.25) we get

(3.26)

Simplifying (3.26) we get,

(3.27)

3.3. Ratio-Cum-Product Estimator in Two Phase Sampling (No Information Case)

If we estimate a study variable when information on all auxiliary variables is unavailable from population, it is utilized in the form of their means. By taking the advantage of Ratio-cum-Product technique for two-phase sampling, a generalized estimator for estimating population mean of study variable Y with the use of multi auxiliary variables is suggested as:

(3.28)

Using (1.0) and (1.5) in (3.28), we get

(3.29)

Using (1.4) in (3.29) and ignoring the second and higher terms for each expansion of product and after simplification we can write as,

(3.30)

Mean squared error of estimator is given by,

(3.31)

We differentiate the equation (3.31) partially with respect to and then equate to zero, using (1.5) and (1.7), we get.

(3.32)

(3.33)

Using normal equation that are used to find the opt mum values given (3.43) we can write,

(3.34)

Or

(3.35)

Using (1.2) in (3.35) we get,

(3.36)

Substituting Equation (3.32) and (3.33) in (3.36) we get

(3.37)

Or

(3.38)

Or

(3.39)

Using (1.6) in (3.39) we get,

(3.40)

Simplifying (3.40) we get,

(3.41)

3.4. Bias and Consistency of Ratio-Cum-Product Estimators

These Ratio-cum-product estimators using multiple auxiliary variables in two phase sampling are biased. However, these biases are negligible for moderate and large samples. It’s easily shown that the Ratio-cum-product estimators are consistent estimators using multiple auxiliary variables since they are linear combinations of consistent estimators it follows that they are also consistent.

4. Simulation, Results and Conclusion

In this section, we carried out data simulation experiments to compare the performance of Ratio-cum product estimator in two phase sampling using multiple auxiliary variables with already existing estimator of finite population that uses one or multiple auxiliary attributes. The data for the empirical study are a normally distributed with the following parameter,

N = 300, n = 45, Mean = 45, standard deviation = 5

, , , , ,

, ,

In order to evaluate the efficiency gain we could achieve by using the proposed estimators, we have calculated the variance of mean per unit and the Mean squared error of all estimators we have considered. We have then calculated Percent relative efficiency of each estimator in relation to variance of mean per unit. We have then compared the Percent relative efficiency of each estimator, the estimator with the highest Percent relative efficiency is considered to be the most efficient than the other estimator. The efficiency is calculated using the following formula

(4.0)

The Table 1 shows percent relative efficiency of proposed estimator with respect to mean per unit estimator for two phase sampling. It is observed that ratio and product estimators using one auxiliary variable are more efficient than mean per unit in the two populations. Again, ratio and product estimator using multiple auxiliary variable are more efficient than mean per unit and ratio and product estimator using one auxiliary variable. Finally, Ratio-cum-product estimator using multiple auxiliary variable is the most efficient of the five estimators in the two populations since it has the highest percent relative efficiency.

The Table 2 shows percent relative efficiency of Ratio-cum-product estimators with respect to mean per unit estimator in two phase sampling. It is observed that the ratio-cum-product estimators are more efficient than mean per unit in the second phase sampling.

Finally, Table 3 compares the efficiency of full information case and partial case to no information case and full to partial information case. It is observed that the full information case and partial information case are more efficient than no information case because they have higher Percent Relative Efficiency than no information case. In addition, the full information case is more efficient than the partial information case because it has a higher Percent Relative Efficiency than partial information case.

Table 1. Relative efficiency of existing and proposed estimator with respect to mean per unit estimator for two phase sampling.

Table 2. Relative efficiency of mean per unit estimator with respect to the proposed ratio-cum-product estimator under full, partial and no information case in two phase sampling.

Table 3. Comparisons of full, partial and no information cases for proposed ratio-cum-product estimator using multiple auxiliary variables.

5. Conclusions

According to Table 1 the proposed Ratio-cum-product estimator using multiple auxiliary variables in two phase sampling has the highest Percent relative efficiency compared to mean per unit, Ratio and Product estimator using one auxiliary variable and Ratio and Product estimator using multiple auxiliary variables in the five simulated populations. This means that the Ratio-cum-product estimator in two phase sampling is the most efficient estimator compared to the estimators that utilize auxiliary variables.

We compared the efficiency of full and partial information case to no information case and found that the two are more efficient than the no information case. We also compared the efficiency of full information case to partial information case and found that the full information case is more efficient than the partial information case. This is clear from Table 2.

Ratio-cum-product estimator using multiple auxiliary attributes in full information case in two phase sampling is recommended to estimate population mean as it outperform other estimator in two phase sampling. If some auxiliary attributes are known, the Ratio-cum-product estimator using multiple auxiliary attributes in partial information case should be used but if all the auxiliary attributes are unknown, Ratio-cum-product estimator using multiple auxiliary attributes in no information case should be used to estimate finite population mean. This is clear from Table 3.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Neyman, J. (1938) Contributions to the Theory of Sampling Human Populations. Journal of the American Statistical Association, 33, 101-116. http://dx.doi.org/10.1080/01621459.1938.10503378
[2]	Cochran, W.G. (1940) The Estimation of the Yields of the Cereal Experiments by Sampling for the Ratio of Grain to Total Produce. Journal of Agricultural Science, 30, 262-275. http://dx.doi.org/10.1017/S0021859600048012
[3]	Hansen, M.H. and Hurwitz, W.N. (1943) On the Theory of Sampling from Finite Populations. The Annals of Mathematical Statistics, 14, 333-362. http://dx.doi.org/10.1214/aoms/1177731356
[4]	Olkin, I. (1958) Multivariate Ratio Estimation for Finite Populations. Biometrika, 45, 154-165. http://dx.doi.org/10.1093/biomet/45.1-2.154
[5]	Murthy, M.N. (1964) Product Method of Estimation. Sankhya, 26, 294-307.
[6]	Robson, D.S. (1952) Multiple Sampling of Attributes. Journal of the American Statistical Association, 47, 203-215. http://dx.doi.org/10.1080/01621459.1952.10501164
[7]	Singh, M.P. (1967) Multivariate Product Method of Estimation for Finite Populations. Journal of the Indian Society of Agricultural Statistics, 31, 375-378.
[8]	Raj, D. (1965) On a Method of Using Multi-Auxiliary Information in Sample Surveys. Journal of the American Statistical Association, 60, 154-165. http://dx.doi.org/10.1080/01621459.1965.10480789
[9]	Singh, M.P. (1967b) Ratio Cum Product Method of Estimation. Metrika, 12, 34-43. http://dx.doi.org/10.1007/BF02613481
[10]	John, S. (1969) On Multivariate Ratio and Product Estimators. Biometrika, 56, 533-536. http://dx.doi.org/10.1093/biomet/56.3.533
[11]	Srivastava, S.K. (1971) A Generalized Estimator for the Mean of a Finite Population Using Multi-Auxiliary Information. Journal of the American Statistical Association, 66, 404-407. http://dx.doi.org/10.1080/01621459.1971.10482277
[12]	Robson, D.S. (1952) Multiple Sampling of Attributes, Journal of the American Statistical Association, 47, 203-215. http://dx.doi.org/10.1080/01621459.1952.10501164
[13]	Ahmad, Z. (2007) Generalized Multivariate Ratio and Regression Estimators for Multi-Phase Sampling. Ph.D. thesis submitted to National College of Business Administration & Economics Lahore 40E-I, Gulberg III, Lahore, Pakistan.
[14]	Samiuddin, M. and Hanif, M. (2007) Estimation of Population Mean in Single and Two Phase Sampling with or without Additional Information. Pakistan Journal of Statistics, 23, 99-118.
[15]	Arora, S. and Bansi, Lal. (1989) New Mathematical Statistics. Satya Prakashan, New Delhi.