Received 6 July 2016; accepted 6 August 2016; published 9 August 2016

1. Introduction
Over the past 30 years RCWA formulated by Moharam and Gaylord [1] - [5] has been used successfully and accurately to analyze periodic structures including holographic gratings [1] [2] and arbitrary profiled dielectric or metallic surface-relief gratings [3] [6] - [8] . RCWA is almost used to study relatively simple structure, such as one-layer gratings [1] - [5] and one-whole gratings [6] - [13] which have arbitrary profiled surface-relief on both of top and bottom of monolithic materials. Owing to its complexity and difficulty, RCWA is seldom used to study multi-layers grating.
In this paper, RCWA is adopted to solve sandwich gratings (SG) structure, which is composed of two identical planar dielectric gratings adjoined by thin metallic or dielectric film. The electromagnetic analytic expressions for each layer of SG structure are given and rigorous coupled-wave equations are deduced. To verify the theory presented in the paper, the proposed RCWA for SG and classic electromagnetic theory are respectively used to research two degenerative SG structures, namely classical single grating and classical single planar structure. The results indicate that RCWA for SG has backwards compatibility and is self-consistent with the classical theory.
2. The Sandwich Grating Structure and Theoretical Formulas
A schematic diagram of the proposed Sandwich grating structure is shown in Figure 1. The configuration consists of two identical planar sinusoidal dielectric gratings of thickness d adjoined by continuous thin silver or dielectric film of thickness h. The lossless planar dielectric grating [1] [2] is characterized by a periodical medium. The relative permittivity can be depicted
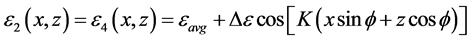 (1)
(1)
where 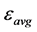 is the average permittivity and
is the average permittivity and  is the amplitude of the sinusoidal permittivity.
is the amplitude of the sinusoidal permittivity. 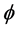 is the grating slant angle and
is the grating slant angle and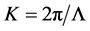 , here
, here 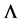 is the grating period. The permittivity in the region I (
is the grating period. The permittivity in the region I (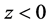 ) is
) is 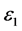 and the ones in the region V (
and the ones in the region V (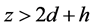 ) is
) is . While the permittivity of Ag film in the region III is
. While the permittivity of Ag film in the region III is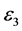 . The complex permittivity of metallic films is described by the Drude model
. The complex permittivity of metallic films is described by the Drude model
 (2)
(2)
where 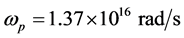 is the plasma frequency for Ag and
is the plasma frequency for Ag and 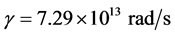 is the collision frequency for Ag [14] ,
is the collision frequency for Ag [14] , .
.
For E-mode polarization (the electric field is in the plane of incidence), the magnetic field is solely in the y direction. According to rigorous coupled-wave analysis theory (RCWA) [1] - [5] , the normalized magnetic fields in each region may be expressed as:
Region I ![]() (3)
(3)
![]()
Figure 1. Schematic diagram of Sandwish grating structure.
Region II ![]() (4)
(4)
Region III ![]() (5)
(5)
Region IV ![]() (6)
(6)
Region V ![]() (7)
(7)
And![]() ,
, ![]() are the space harmonic magnetic-field amplitudes and satisfy coupled-wave equations in grating regions. The solutions for
are the space harmonic magnetic-field amplitudes and satisfy coupled-wave equations in grating regions. The solutions for![]() ,
, ![]() are referenced from the Ref. [2] and may be expressed as:
are referenced from the Ref. [2] and may be expressed as:
![]() ,
, ![]() where
where ![]() and
and ![]() are the eigenvalues and eigenvectors.
are the eigenvalues and eigenvectors.
The second grating in Region IV is the same modulated as the first grating, so their eigenvalues and eigenvectors are also the same. But owing to the different boundary conditions of tangential electric and magnetic fields, the coefficients ![]() are different. On the other hand, the normalized wave amplitudes of the thin connected region (Region III) are determined by the interactions between the forward-diffraction of the first grating and backward-diffraction of the second grating.
are different. On the other hand, the normalized wave amplitudes of the thin connected region (Region III) are determined by the interactions between the forward-diffraction of the first grating and backward-diffraction of the second grating.
The symbols used in Equations (3)-(7) are as follows:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where i is the space-harmonic index in grating Regions II and IV (analogous to the diffractive order index in Regions I, III and V), ![]() is the angle of incidence,
is the angle of incidence, ![]() is the free-space wavelength.
is the free-space wavelength. ![]() are the normalized amplitude of the ith reflected and transmitted wave of Region I, Region III or Region V.
are the normalized amplitude of the ith reflected and transmitted wave of Region I, Region III or Region V.
The electromagnetic boundary conditions require that the tangential components of the electric field and the magnetic field must be continuous across planes![]() ,
, ![]() ,
, ![]() and
and![]() . The boundary conditions for tangential magnetic field (
. The boundary conditions for tangential magnetic field (![]() ) are respectively
) are respectively
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
The tangential electric field ![]() may be obtained from the Maxwell curl equation
may be obtained from the Maxwell curl equation![]() . The result is
. The result is ![]() and boundary conditions for tangential electric field (
and boundary conditions for tangential electric field (![]() ) are respectively
) are respectively
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
where![]() .
.
If N values of i are retained in the analysis, there will be 4N unknown values of ![]() and they will be determined from the boundary conditions. All the
and they will be determined from the boundary conditions. All the ![]() may then be calculated.
may then be calculated.
The backward-wave diffraction efficiencies (Region I) are
![]() (19)
(19)
The forward-wave diffraction efficiencies (Region V) are
![]() (20)
(20)
3. Numerical Calculations and Discussions
In order to verify the deduced formulas above, the reflection and transmission characteristics of Sandwich gratings connected by thin silver film are studied in the condition of grating thickness ![]() at normal incidence. The other parameters are as follows,
at normal incidence. The other parameters are as follows,![]() . The five calculated regions shown in Figure 2(a) are degenerated into three regions shown in Figure 2(b). The proposed RCWA for SG and classic electromagnetic theory are respectively used to solve for the reflection and transmission characteristics. The efficiencies of results given by RCWA in the paper and classical theory are both shown in Figure 3. The discrepancy magnitude between two methods is only
. The five calculated regions shown in Figure 2(a) are degenerated into three regions shown in Figure 2(b). The proposed RCWA for SG and classic electromagnetic theory are respectively used to solve for the reflection and transmission characteristics. The efficiencies of results given by RCWA in the paper and classical theory are both shown in Figure 3. The discrepancy magnitude between two methods is only ![]() shown in Figure 4, which proves our formulas and computer program codes to be true. Our work backwards contains the results of the classical Fresnel formulas of three regions.
shown in Figure 4, which proves our formulas and computer program codes to be true. Our work backwards contains the results of the classical Fresnel formulas of three regions.
Furthermore, when the connection layer of thin metallic film is absence, namely![]() , the proposed Sandwich grating is simplified into an ordinary one-layer grating. The unslant grating has 400 nm grating period and 100 nm thickness, and its average permittivity is 2.25 with the modulation 0.33. The thickness of the connection layer of thin Ag film is zero. On this condition, the two same gratings are combined to be one whole thick grating of 200 nm, shown in Figure 5(b). Suppose the grating in water, thus
, the proposed Sandwich grating is simplified into an ordinary one-layer grating. The unslant grating has 400 nm grating period and 100 nm thickness, and its average permittivity is 2.25 with the modulation 0.33. The thickness of the connection layer of thin Ag film is zero. On this condition, the two same gratings are combined to be one whole thick grating of 200 nm, shown in Figure 5(b). Suppose the grating in water, thus![]() .
.
The efficiencies of reflection and transmission of single layer gratings calculated by our theory and by classical Rigorous Coupled-wave Approach are both shown in Figure 6. The results are nearly the same.
From the above discussed, the correctness and efficiencies of RCWA for SG are verified. The theory given in the paper has backwards compatibility and is self-consistent with the classical theory.
4. Conclusion
Rigorous coupled-wave approach for SG is proposed in the paper. The proposed RCWA for SG and classic electromagnetic theory are respectively used to study two degenerative SG structures, and the reflection and
![]()
Figure 2. (a) Sandwish grating structure; (b) classical planar structure.
![]()
Figure 4. Calculation discrepancy between our program and Fresnel equations.
![]()
Figure 5. (a) Sandwish grating; (b) Combined into single layer grating.
transmission spectra are almost the same. The results indicate that RCWA for SG has backwards compatibility and is self-consistent with the classical theory. The theoretical formula and computer codes lay the foundations for investigation of properties of the novel Sandwich grating and exploitation of nano-photonics devices.
Acknowledgements
The author appreciates the support from National Natural Science Foundation of China under Grant No. 61275083.