On Two Birkhoff-Type Interpolations with First- and Second-Order Derivative

Tinggang Zhao, Yongjun Li

School of Mathematics, Lanzhou City University, Lanzhou, China.

DOI: 10.4236/jamp.2016.47133                

Abstract

In this paper, we consider two interpolations of Birkhoff-type with integer-order derivative. The Birkhoff interpolation is related with collocation method for the corresponding initial or boundary value problems of differential equations. The solvability of the interpolation problems is proved. For Gauss-type interpolating points, error of interpolation approximation is deduced. Also, we give efficient algorithms to implement the concerned interpolations.

Keywords

Birkhoff Interpolation, Collocation Method, Gauss-Type Interpolating Point, Error Estimation

1. Introduction

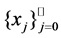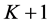Back to 1906, an extension of polynomial interpolation which involves the values of derivatives of the interpolated function is studied by G. D. Birkhoff in [1]. The Birkhoff interpolation (named after G. D. Birkhoff) may be defined as follow. Given a set of distinct interpolating points and data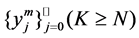, to find a polynomial 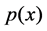of degree 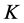such that

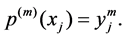(1)

If for each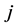, the orders of derivatives in (1) form a unbroken sequence,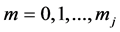. The interpolation problem above refers to Hermite interpolation. But in general, we say the Birkhoff interpolation which means the other case. It turns out that the Birkhoff interpolation problem is difficult and causes many literatures [2]-[7]. In contrast to Lagrange interpolation and Hermite interpolation, a Birkhoff interpolation problem does not always have a unique solution. For instance, there is no quadratic polynomial 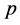such that 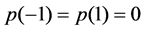an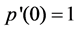. For solvability of Birkhoff interpolation problems, Pòlya condition is suggested in [8] and developed in [9]. To construct the Birkhoff interpolation formulation, an algorithmic approach is presented in [10] for Hermite-Birkhoff interpolation. There are also many results for (0, 2) interpolation [11] and others.

In any way, the approximation theory of interpolation is in foundational importance of numerical analysis even of algorithm method for various scientific computing problems. In [12], authors suggested a well-condi- tioned collocation method based on a Birkhoff interpolation which achieved efficiency in computation. It is necessary to contemplate the Birkhoff interpolation appeared in [12].

This paper is organized as follow. In Section 2, we present the interpolation problems. In Section 3, we give solvability and representation of the problems. In Section 4, we present the interpolation errors. In Section 5, efficient algorithms for computing the interpolation polynomials are given. In Section 6, some conclusive remarks are given.

2. Interpolation Problems

Let 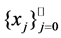be a set of 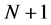distinct interpolating points posed on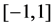, which are arranged in increasingly order, namely

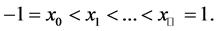
Denote by 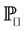the set of all polynomials of degree at most defined on. First of all, we give two definitions of the concerned Birkhoff problems.

Problem 1. For any and, the Birkhoff interpolation of, denoted by, is a polynomial of degree, which satisfies that

, , and (2)

Remark. A similar interpolation for endpoint can be defined by conditions as

, , and

The corresponding results is parallel to theirs for Problem 1.

Problem 2. For any and, the Birkhoff interpolation of, denoted by, is a polynomial of degree, which satisfies that

, , and. (3)

We will verify that the two interpolation problems above are all solvable latterly. In common, it is unexpected that the interpolation or gives a good approximation to for arbitrary interpolating points. In order to achieve good approximation, we will consider the Gauss-type quadrature nodes as the interpolating points. However, solvability of the problems above has nothing to do with the interpolating points.

3. Solvability and Representations

3.1. Solvability of the Problems

For Problem 1, the solvability is equivalent to invertibility of the following matrix

(4)

We now check the matrix (4). The determinant of the matrix (4) is. We claim that the

Problem 1 is solvable from the invertibility of the matrix (4).

For Problem 2, the solvability is equivalent to invertibility of the following matrix

(5)

We now check the matrix (5). By calculus, we know that the determinant of the matrix (5) is

. Then Problem 2 is solvable from the invertibility of the matrix (5).

3.2. Representations of the Interpolation Operators

As with the Lagrange interpolation, we search for a nodal basis to represent the interpolating polynomial. For Problem 1, we need to look for such that

(6)

Theorem 1. The Birkhoff nodal basis has the following formulas:

where

Proof. The proof is direct by computing. Here we omit it.

Making use of the nodal basis in Theorem 1, we have the representation of as

(7)

We now turn to Problem 2. Here need to look for such that

(8)

Theorem 2. The Birkhoff nodal basis has the following formulas:

where

Proof. The proof is in [12].

Making use of the nodal basis in Theorem 2, we have the representation of as

(9)

4. The Interpolation Errors on Gauss-Type Points

In this section, we will analyze the error between the online function and its Birkhoff interpolation approximation on Gauss-type interpolating points. Let be the classical Jacobi orthogonal polynomial of degree exact with index pair. We take Jacobi-Gauss-Lobatto nodes as the interpolating points, namely, , and are the zeros of (also zeros of).

In order to analyze interpolation Problem 1, we introduce the following Lagrange-Gauss-Radau interpolation defined as: for, such that

The following lemma (page 134, Theorem 3.42 in [13]) is important for error estimate.

Lemma 1. For and any, we have that for and,

where is a positive constant independent and.

From the Definitions of two interpolation operators and, we find that

(10)

Now, we come to the following error estimation by combining the result in Lemma 1 with (10).

Theorem 3. Under the assumption of Lemma 1, it holds

(11)

where is a positive constant independent and.

Next, we consider the interpolation Problem 2. We need the following Lagrange-Gauss interpolation defined as: for, such that

The following lemma (page 132, Theorem 3.41 in [13]) is important for error estimate.

Lemma 2. For and any, we have for,

where is a positive constant independent and.

From the Definitions of two interpolation operators and we find that

(12)

Now we come to the following error estimation. Similarly, combining the result in Lemma 2 with (12), we obtain

Theorem 4. Under the assumption of Lemma 2, it holds

(13)

where is a positive constant independent and.

5. Efficient Formulations to Computing the Interpolations

The representation (7) (or (9)) with Theorem 1 (or with Theorem 2) is unconvenience for computing (or). Here, we develop efficient algorithms to deal with them.

Case. Since, we write

(14)

We only need to compute. Derivating (14), we have

(15)

Making use of the orthogonality of Jacobi polynomials, we can obtain for,

Since, the Jacobi-Gauss-Radau quadrature at nodes is exact. At

last, we have

(16)

where is the weight corresponding to quadrature node of Jacobi-Gauss-Radau with the fixed endpoint. Now we only left to determine. It is not difficult because that

(17)

Case. Since, we write

(18)

We need to compute. Derivating (18) twice, we have

(19)

Making use of the orthogonality of Jacobi polynomials, we can obtain for,

Since, the Jacobi-Gauss quadrature at nodes is exact.

At last, we have for

(20)

where is the weight corresponding to quadrature node of Jacobi-Gauss. Now there left and to be determined. In fact,

(21)

and

(22)

For every, we need operations to computing in both cases. The computational complexity is to obtain the interpolation polynomial (14) or (18) assuming that or are all pre-computed.

6. Conclusive Remarks

Two Birkhoff-type interpolations which are related with first-order initial value problem and second-order boundary value problem respectively are considered in the paper. As in [12], this Birkhoff interpolation leads to well-conditioned collocation matrices or pre-conditioner. We remark that it is worthy to consider the similar interpolations for high-order derivative case or fractional-order derivative case.

Acknowledgements

We thank the editor and the referee for their comments. The authors were supported by National Natural Science Foundation of China (Grant No. 11161026 and No. 11261027).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	[1] Birkhoff, G.D. (1906) General Mean Value and Remainder Theorems with Applications to Mechanical Differentiation and Quadrature. Transactions of the American Mathematical Society, 7, 107-136. http://dx.doi.org/10.2307/1986339
[2]	Lorentz, G.G. and Zeller, K.L. (1971) Birkhoff Interpolation. SIAM Journal on Numerical Analysis, 8, 43-48. http://dx.doi.org/10.1137/0708006
[3]	Lorentz, G.G., Jetter, K. and Riemenschneider, S.D. (1983) Birkhoff Interpo-lation. Addison-Wesley Publ. Comp.
[4]	Pólya, G. (1931) Bemerkung zur interpolation und zur N?herungstheorie der dalkenbiegung. Zeitschrift für Angewandte Mathematik und Mechanik, 11, 445-449. http://dx.doi.org/10.1002/zamm.19310110620
[5]	Karlin, S. and Karon, J.M. (1972) On Hermite-Birkhoff Interpolation. Journal of Approximation Theory, 6, 90-114. http://dx.doi.org/10.1016/0021-9045(72)90085-8
[6]	Sharma, A. (1972) Some Poised and Unpoised Problems of Interpolation. SIAM Review, 14, 129-151. http://dx.doi.org/10.1137/1014004
[7]	Shi, Y.G. (2003) Theory of Birkhoff Interpolation. Nova Science Publishers, New York.
[8]	Ferguson, D.R. (1969) The Question of Uniqueness for G. D. Birkhoff Interpolation Problems. Jour-nal of Approximation Theory, 2, 1-28. http://dx.doi.org/10.1016/0021-9045(69)90028-8
[9]	Palacios, F. and Rubió, P. (2003) Generalised Pólya Condition for Birkhoff Interpolation with Lacunary Polynomial. Applied Mathematics E-Notes, 3, 124-129.
[10]	Mühlbach, G. (1981) An Algorithm Approach to Hermite-Birkhoff Interpolation. Numerische Mathematik, 37, 339- 347. http://dx.doi.org/10.1007/BF01400313
[11]	Szili, L. (1996) A Survey on (0,2) Interpolation. Annales Universitatis Scientiarum Budapestinensis de Rolando E?tv?s Nominatae, Sectio Computatorica, 16, 377-390.
[12]	Wang, L.L., Samson, M.D. and Zhao, X.D. (2014) A Well-Conditioned Collocation Method Using a Pseudospectral Integration Matrix. SIAM: SIAM Journal on Scientific Computing, 36, A907-A929. http://dx.doi.org/10.1137/130922409
[13]	Shen, J., Tang, T. and Wang, L.L. (2011) Spectral Methods: Algorithms, Analysis and Applications. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-71041-7