Space-Time Description of Cross Sections and Durations of Neutron-Nucleus Scattering near 1 - 2 Resonances in the C- and L-Systems

V. S. Olkhovsky

Institute for Nuclear Research of NASU, Kiev, Ukraine.

DOI: 10.4236/oalib.1101586                

Abstract

The appearance of time advance (due to distortion by the non-resonant background) instead of the expected time delay in the region of a compound-nucleus resonance in the center-of-mass (C-) system is known. Here at the same conditions we study cross sections and durations of the neutron-nucleus scattering in the laboratory (L-) system. Here there are a review of papers where it is shown that such time advance is a virtual paradox and in the L-system the time-advance phenomenon does not occur and only the trivial time delay is observed. At the same time the transformations from C-system into the L-system appear to be different from the standard kinematical transformations because in the C-system the motion of a compound nucleus is absent but it is present in the L-system. Here we analyze the initial wave-packet motion (after the collision origin) and the cross section in the laboratory (L-) system. Also here (as physical revelations of profound general methodic and in very good consistent accordance with the experiment) several results of the calculated cross sections for the neutron-nucleus in comparison with the experimental data in the L-system at the range of one or two overlapped compound resonances are presented. It is shown in the space-time approach that the standard cinematic transformations of cross sections from the C-system to the L-system are not valid because it is necessary to consider the center-of-mass motion in the L-system. Finally on a correct self-consistent base of the space-time description of the nuclear processes in the laboratory system with 3 particles in the final channel, the validity of the former approach is shown, which is obtained for the space-time description of the nuclear processes with 2-particle channels earlier.

Keywords

Space-Time Approach to Nuclear Collision, Time Delay, Time Advance, Transformations of Cross Sections from the C-System to the L-System, Interference Phenomena

Subject Areas: Nuclear Physics, Quantum Mechanics

1. Introduction

The phenomenon of time advance instead of expected time delay in the C-system was found in [1] - [8] . This phenomenon is usually accompanied by a cross section minimum for almost the same energy. Then naturally the question had arisen if this advance manifested also in the L-system?

Then in [8] - [10] it was found that the standard formulas of cross section transformations from the L- to C- system were inapplicable in the cases of two (and more) collision mechanisms. Usually the delay-advance phenomenon in nucleon elastic is scattered by nuclei near a resonance and distorted by the non-resonant background (in the C-system). Usually (see, for instance, [1] - [3] ) the amplitude F_C(E, θ) for the elastic scattering of nucleons by spherical nuclei near an isolated resonance in the C-system can be written as

, (1)

where

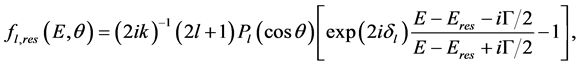
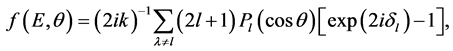
here, and G are the excitation energy, the resonance energy and the width of the compound nucleus, respectively; we neglect the spin-orbital interaction and consider a comparatively heavy nucleus.

Rewriting (1) in the form

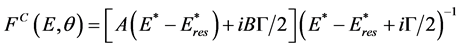, (1a)

where

,

,

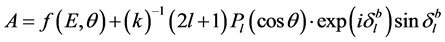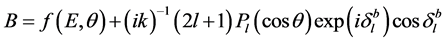we obtain the following expression for the scattering duration: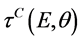

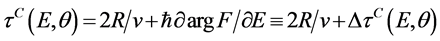(2)

in case of the quasi-monochromatic particles which have very small energy spreads. Formula (2) was obtained in [1] . In Formula (2), v = ħk/m is the projectile velocity, R is the interaction radius, and Dτ^C is

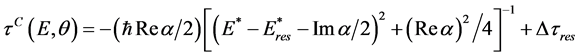, (3)

with

(4)

From (3) one can see that, if 0 < Rea < G, the quantity Dτ(E,θ) appears to be negative in the energy interval ~ Rea around the center at the energy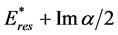. When the minimal delay time can obtain the value. Thus, when Rea ® 0⁺, the interference of the resonance and the background scattering can bring as much as desired large of the advance instead of the delay! Such situation is mathematically described by the zero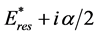, besides the pole, of the amplitude F^C(E, θ) (or the correspondent T-matrix) in the lower unphysical half-plane of the complex values for energy E. We should notice that a very large advance can bring to the problem of causality violation (see, for instance the note in [2] ). The delay-ad- vance phenomenon in the C-system was studied in [1] - [3] for the nucleon-nucleus elastic scattering.

For two overlapped resonances, the scattering amplitude for an elastic reaction can be written in center-of- mass system also in form (1):

where

(5)

and already

, (6)

we obtain the following expression for the total scattering duration τ^C(E, θ)

for the quasi-monochromatic particles which have very small energy spreads, when one can use the method of stationary phase for approaching the group velocity of the wave packet.

In Figure 1 and Figure 2 we can see the energy dependence of for two couples of overlapped

Figure 1. Energy dependence of near two overlapped resonances ⁵⁸Ni and.

Figure 2. Energy dependence of near two overlapped resonances ⁵⁸Ni and.

resonances [8] .

2. The Collision-Process Diagram with 2 Mechanisms (Direct Process and Collision with the Formation of a Compound Nucleus)

In Figure 3(a) and Figure 3(b) these two processes in the L-system are pictorially presented. They represent a prompt (direct) and a delayed compound-resonance mechanism of the emitting y particle and Y nucleus, respectively. The both mechanisms are macroscopically schematically indistinguishable but they are microscopically different processes:

Figure 3(a) represents the direct process of a prompt emission of the final products from the collision point C₀ with a very small time duration τ_dir, while Figure 3(b) represents the motion of a compound-resonance nucleus Z^* from point C₀ to point C₁, where it decays by the final products y + Y after traveling a distance between C₀ and C₁ which is equal to ~V_CDτ_res before its decay. Here V_C is the compound-nucleus velocity, equal to the

center-of-mass velocity, and is the mean time of the nucleus Z^* motion

before its decay [9] - [12] for the case of one compound resonance, the energy spread DE of the incident particle x being very small in comparison with the resonance width G, E_Z = E^*,. For the clarity of the difference between both processes in time, we impose the evident practical condition

. (7)

For the macroscopically defined cross sections, in the case of very large macroscopic distances r₁ (near the detector of the final particle y) with very small angular and energy resolution (and), the angles θ₁ and, as well as momentums k₁ and, can be considered as practically coincident. Really, and with. Using the usual macroscopic definition of the cross section with the help of some transformations for the exit asymptotic wave packet of the system y + Y, in [4] it was obtained the following expression for the cross section σ of reaction (4) in the L-system:

, (8)

where

, (9)

, (10)

(a) (b)

Figure 3. (a) Diagram of the direct process; (b) Diagram of process with the compound nucleus.

, (11)

, (12)

(13)

is the projection of the Z-nucleus velocity to the direction of, d_l is the l-wave scattering background phase shift. Formulas (8)-(11) were obtained for a quasi-monochromatic incident beam and a very small angular and energy resolution (,) of the final-particle detector.

For the simplicity we neglect here the spin-orbital coupling and we suppose also that the absolute values of all differences r_n/v_n ? r_p/v_p (n ¹ p = 1,2) are much less than the time resolutions. Here J_C→L is the standard Jacobian of pure cinematic transformations from the C-system to the L-system.

We underline that Formulas (8)-(13) for the cross section σ, obtained in [9] - [12] and defined by the usual macroscopic way, take into account a real microscopic motion of the compound nucleus. So, the Formulas (8)-(13)

differ from the standard kinematical transformation of from the C-system into the L-

system, considering only the kinematical transformations of the energies and angles from the C-system (with φ = 0) to the L-system. Such difference arises because the formal expression for σ^C(E,θ) as taken without consideration of the microscopic difference between the processes in Figure 3(a) and Figure 3(b), and thus without consideration of the parameter,.

3. The Lack of Time Advance near Compound-Resonances in the L-System

We underline that Formulas (8)-(13) for the cross section σ, obtained here, are defined by the usual macroscopic way and also consider the real microscopic motion of the compound nucleus which strongly differ them from

the standard cinematic transformation from C-system into L-system namely by the interference of the amplitudes and, (where). The parameter φ reflects the influence of the compound-nucleus motion.

In the first my works (for instance, in [1] - [3] ) usually the analysis of the amplitudes, cross sections and durations of the elastic scattering performed on the base of Formulas (1)®(1a) in C-system, in which the compound-nucleus motion in L-system did not taken into account. But taking in account the motion of the decaying compound nucleus in L-system the expressions for the amplitude of the collision process which is going on with the formation of excited compound nucleus in the region of a resonance in C- and L-systems differ not only by the standard cinematic transformations {E^C, θ^C}«{E^L, θ^L}, but also taking into account of the motion of the decaying compound nucleus along the distance V_CDτ_res, as it was shown in Figure 3(a) and Figure 3(b). In [1] - [3] Formulas (1) and (1a) were written in C-system and are described the coherent sum of the interfering terms for

the both of cross section and the time delay Dτ^C(E,θ) without the microscopic motion

of the decaying compound nucleus from point C₀ till point C₁. It is possible to evaluate the general duration of collision in L-system, taking the superposition of the wave packets of the direct scattering and of the scattering, going on with the formation of the intermediate compound nucleus (in the correspondence with diagrams 1a and 1b, respectively) which was obtained in [9] , and in the asymptotic range (for r® ∞) after all the simplifications, considering the conservation of energy-impulse, receives the form

(14)

where, , is the projection of the nucleus Z^* motion velocity on the k_1,2

direction, t_i is the initial time moment, defined by the amplitude phase of the initial weight factor g_i, chosen for

the simplicity in the Lorentzian form with the very small of the energy spread; is the kinetic energy of the l-th particle with mass m_l (l = 1, 2), correspondent to par

ticles y and Y, respectively. Тhen, utilizing the general approach from [13] [14] for the mean collision duration

(15)

(with for quasi-monochromatic particles), we obtain after all the simplifications, mentioned in [8] and utilized here, the result, which consists in that, that the general time delay соrresponds to the time-energy uncertainty relation for quasi-monochromatic particles (for which and).

Thus, we obtain the trivial mean time delay in the approximation and for L-system without any advance, caused by “virtual unmoving” compound nucleus in C-system. Formulas (8)-(13) are the result of the self-consistent approach to the realistic analyze of the experimental data on the cross sections of nucleon-nucleus scattering in L-system. And any attempt to describe the experimental data of the nucleon-nuc- leus-scattering cross sections near an isolated resonance, distorted by the non-resonance background, in L-sys- tem on the simple base of Formula (1) in C-system with the further use of the standard cinematic relations {E^C,θ^C}«{E^L,θ^L} in L-system does not have any practical physical sense. And the reason of it is connected with that we neglect the real motion of the compound nucleus.

For the case of two overlapped resonances [15] we have to calculate the wave function quite similarly to the case of one resonance before:

(16)

Here, , where is the projection of the speed of nucleus Z^* on the vec

tors, t_i is initial moment of time.

To calculate the time of delay in the L-system we have to use this formula:

, (17)

where is the initial current.

So, if we will take into account the movement of the compound-nucleus the advanced time vanishes also here.

4. Оn Cross Sections of Neutron-Nucleus Scattering Near a Couple of Overlapped Compound-Nucleus Resonances in the C- and the L-System

We have calculated the excitation functions σ(E) for the low-energy elastic scattering of neutrons by nuclei ⁵²Cr and ⁵⁶Fe and in the region of distorted isolated resonances E_res = 50.5444 keV and G = 1.81 keV, Е_res = 27.9179 keV and 0.71 keV, respectively. The values of the parameters for the amplitudes of the direct and resonance scattering separately in C-system for l = 0 (and, naturally, without the Coulomb phases) in formulas (8)-(13) were selected with the help of the standard procedure. The fitting parameter c was chosen to be equal to 0.68p or 0.948π or 0.956π or p, respectively.

The calculation results were obtained with the help of Formulas (8)-(13) in the comparison with the experimental data, given from [16] . They are represented in Figures 4-6, respectively. Аnd the results of calculations performed by the standard cinematic formulas from C- into L-system (i.e. by the Formulas (8)-(13) but with φ º 0, that is without diagram, depicted in and Figure 3(b) are represented in Figures 4(а)-6(а). One can see that for φ º 0 the minima are not totally filled.

5. The Cross Sections of the Neutron-Nucleus Scattering with Two Overlapped Resonances

If we want to take into consideration the moving of the compound nucleus, we have to use another formula for cross section:

(18)

where

, (19)

(a) (b)

Figure 4. (a) The excitation function for ⁵²Cr(n, n); (b) The excitation function for ⁵²Cr(n, n) with j º 0.

(a) (b)

Figure 5. (a) The excitation function for ⁵⁶Fe(n, n); (b) The excitation function for ⁵⁶Fe(n, n) with j º 0.

(a) (b)

Figure 6. The excitation function for ⁵⁸Ni near two overlapped resonances with and; (b) The excitation function for ⁵⁸Ni with φ = 0 near two overlapped resonances. with and.

. (20)

We can calculate phase Ф the same way, as in the case with the one resonance.

Other values can be found this way:

, (21)

(22)

In Figure 6(a) and Figure 6(b) we can see theoretical function according to (18)-(22) and experimental data. The method of least squares was used to fit the function and experimental data. Experimental data where taken from [17] . After approximation we had such values of the parameters:, , , , ,:

After approximation we had such values of the parameters

:, , , , , ,

6. Conclusions and Perspectives

Time analysis of experimental data on nuclear processes is presented here to make the following conclusions and perspectives:

1) The simple application of time analysis of quasi-monochromatic scattering of neutrons by nuclei in the region of isolated resonances, distorted by the non-resonance background, brings in C-system to the delay-ad- vance paradoxical phenomenon near a resonance in any two-particle channel. Such phenomenon of the time- transfer delay in the time advance is usually connected with a minimum in the cross section, or zero in analytic plane of scattering amplitude (apart from the resonance pole) near the positive semi-axis of kinetic energies in lower non-physical semi-plane of the Riemann surface. Here this paradox is eliminated by the thorough space- time analysis in L-system with moving C-system.

2) Moreover, it is also revealed that the standard formulas of transformations from L-system into C-system are in-suitable in the presence of two (and more) collision mechanisms―quick (direct or potential) process when the center-of-mass is practically not displaced in the collision and the delayed process when the long-li- ving compound nucleus is moving in L-system. And revealed by our group the additional change of the amplitude phase in C ® L transformations now agrees with the elimination of the paradox of passing the usual time delay in the time advance. The obtained analytic transformations of the cross section from C-system into L-sys- tem are illustrated by the calculations of excitation functions for examples of the elastic scattering of neutrons by nuclei ⁵²Cr, ⁵⁶Fe and ⁵⁸Ni near the distorted resonances in L-system.

3) The presented results of time analysis for quasi-monochromatic nucleon-nucleus scattering near the isolated resonances, distorted by the non-resonance background, can be easily generalized to the scattering nucleons by nuclei near two - three overlapped resonances.

4) Of course, new Formulas (8)-(13) and (18)-(22) can be also used for the improvement of the existing general methods of analyzing resonance nuclear data for the two-particle channels in nucleon-nucleus collisions in L-system and, moreover, can be generalized for more complex collisions.

5) Applying time analysis to elastic nucleon-nucleus with 2 - 3 overlapping compound-resonances, it is possible also to obtain the paradoxical phenomenon of transition decay in advance in C-system. But the behavior of amplitudes and durations can be certainly more complex than for an isolated resonance. Therefore the study of such cases can be more complicated than for an isolated resonance, and it has to be rather interesting and perspective.

7) It is rather interesting to apply the results of the space-time description of direct and sequential (via compound-nucleus) processes in the L-system of nuclear reactions with three particles in the final channel for concrete investigations, elaborations and calculations of many concrete nuclear collisions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Olkhovsky, V.S. and Doroshko, N.L. (1992) Cross-Sections and Durations of the Proton-Nucleus Scattering near a Resonance Distorted by the Nonresonance Background and Their Phase-Shift Analysis. Europhysics Letters, 18, 483. http://dx.doi.org/10.1209/0295-5075/18/6/002
[2]	D’Arrigo, A., Doroshko, N.L., Eremin, N.V., Olkhovsky, V.S., et al. (1992) Bremsstrahlung Study of Nuclear-Reaction Dynamics: The 16O + p Reaction. Nuclear Physics A, 549, 375-386. http://dx.doi.org/10.1016/0375-9474(92)90085-x
[3]	D’Arrigo, A., Doroshko, N.L., Eremin, N.V., Olkhovsky, V.S., et al. (1993) Delay-Advance Phenomenon Observed by Bremsstrahlung Spectrum of the 12C + p Collision. Nuclear Physics A, 564, 217-226. http://dx.doi.org/10.1016/0375-9474(93)90518-3
[4]	Kelkar, N.G. (2003) Time Advancement in Resonance Regions of πN Scattering. Journal of Physics G: Nuclear and Particle Physics, 29, L1-L8. http://dx.doi.org/10.1088/0954-3899/29/2/101
[5]	Kelkar, N.G., Nowakowski, M. and Khemchandani, K.P. (2003) Collision Times in ππ and πK Scattering and Spectroscopy of Meson Resonances. Nuclear Physics A, 724, 357-374.
[6]	Kelkar, N.G., Nowakowski, M., Khemchandani, K.P. and Jain, B.K. (2004) Time Delay Plots of Unflavoured Baryons. Nuclear Physics A, 730, 121-140.
[7]	Kelkar, N.G., Khemchandani, K.P. and Jain, B.K. (2006) Interaction of Eta Mesons with Nuclei. Journal of Physics G: Nuclear and Particle Physics, 32, 3L19.
[8]	Prokopets, G.A. (2011) Calculation of the Angular Distribution of Delay Times in Neutron Scattering on 58Ni Nuclei. Physics of Atomic Nuclei (Russia), 74, 714-720.
[9]	Eremin, N.V.,Giardina, G., Olkhovsky, V.S. and Omelchenko, S.A. (1994) Temporal Description of Interference Phenomena in Nuclear Reactions with Two-Particle Channels. Modern Physics Letters A, 9, 2849. http://dx.doi.org/10.1142/S0217732394002690
[10]	Olkhovsky, V.S., Dolinska, M.E., Omelchenko, S.A. and Romanyuk, M.V. (2010) New Developments in the Tunneling and Time Analysis of Low-Energy Nuclear Processes. International Journal of Modern Physics E, 19, 1212-1219.
[11]	Olkhovsky, V.S., Dolinska, M.E. and Omelchenko, S.A. (2011) On Scattering cross Sections and Durations near an Isolated Compound-Resonance, Distorted by the Non-Resonant Background, in the Center-of-Mass and Laboratory Systems. Applied Physics Letters, 99, Article ID: 244103. http://dx.doi.org/10.1063/1.3656705
[12]	Olkhovsky, V.S., Dolinska, M.E. and Omelchenko, S.A. (2012) On the Cross Section and Duration of the Neutron-Nucleus Scattering with a Resonance, Distorted by a Non-Resonant Background, in the Center-of-Mass System and Laboratory System. Proceedings of the 4th International Conference on Current Problems in Nuclear Physics and Atomic Energy (NPAE-2012), Kyiv, 3-7 September 2012, 198-201.
[13]	Olkhovsky, V.S. (1984) Investrigation of Nuclear Reactions and Decays by Analysis of Their Duration. Sov. J. Particles Nucl. (Engl. Transl.).(United States), 15, 130-148.
[14]	Olkhovsky, V.S. (2009) Time as a Quantum Observable, Canonically Conjugated to Energy, and Foundations of Self-Consistent Time Analysis of Quantum Processes. Advances in Mathematical Physics, 2009, Article ID: 859710, 83 p. http://dx.doi.org/10.1155/2009/859710
[15]	Olkhovsky, V.S., Doroshko, N.L. and Lokotko, T.I. (2013) On the Cross Section and Duration of the Neutron-Nucleus Scattering with Two Overlapped Resonances in the Center-of-Mass System and Laboratory System. Proceedings of the 4th International Conference on Current Problems in Nuclear Physics and Atomic Energy (NPAE), Kyiv, 3-7 September 2012, 192-197.
[16]	Harvey, J.A. and Larson, D.C. (1974) The JEFF—3.1.1. Nuclear Data Library, OECD NEA/NEA2009; EXFOR 13759.002, ORNL.
[17]	Brusegan, A., Rohr, G., Shelley, R., Macavero, E., Van Der Vorst, C., Poortmans, F., Mewissen, I. and Vanpraet, G. (1994) Very High Resolution Transmission Measurements and Resonance Parameters of Ni58 and Ni60.