A Tree-Based Distributed Permutation Routing Protocol in Multi-Hop Wireless Sensors Network ()
Received 6 November 2015; accepted 20 June 2016; published 23 June 2016
1. Introduction
WSN is an ad-hoc network, which is made up of small devices deployed in an area called capturing field in order to study one or more phenomena [1], [2]. Commonly monitored parameters are temperature, humidity, pressure, wind direction and speed, illumination intensity, vibration intensity, sound intensity, power-line voltage, and chemical [3]. Generally, the field of capture is an area where access is almost impossible for humans [4]. Therefore, to ensure a maximum performance of sensors, it is necessary to develop an efficient routing protocol that reduces the power consumption of the later. This is particularly important in the measure that energy spend by a sensor to send or to receive an item can be used to process a thousands of operations [5]. One of the communication techniques in the WSNs is the multi-hop communication. It ensures the sending of captured data to a station using intermediate stations. The main goal is to partition a given WSN into disjoint clique in which, a Cluster Head (CH) is elected for each clique. After that, we present a new Hierarchical permutation routing protocol which is not only energy efficient, but also reduces the work of CHs. To achieve this, we propose to use the technique of channel reservation presented in [6], the clustering technique presented in [4], and other techniques presented in [7]-[10].
1.1. State of the Art
The fundamental goal of a sensor network is to produce, over an extended period of time, globally meaningful information from raw local data obtained by individual sensor nodes. Importantly, this goal must be achieved in the context of prolonging as much as possible the useful lifetime of the network and ensuring that the network remains highly available and continues to provide accurate information in the face of security attacks and hardware failure [11]. WSNs experienced a great expansion these latest years. In fact, many works had been done in this domain; especially in the data routing and more precisely in permutation routing in a multi-hop environment. Bomgni et al. in [8] have introduced a deterministic routing protocol for permutation routing in dense multi-hop sensor networks, which is realized in 
broadcast rounds in the worst case. Lakhlef et al. proposed in [7] an improvement of the previous protocol that runs in 
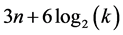broadcast rounds. Where n is the number of items stored in the network, p is the number of sensors, 
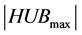is the number of sensors in the clique of maximum size and k is the number of cliques after the first clustering. However, the protocols presented in [8] and [9] assume that all network stations are awake during the entire execution of the protocols.
Heinzelman et al. [12] introduced a hierarchical clustering algorithm for sensor networks, called Low Energy Adaptative Clustering Hierarchy (LEACH). LEACH is a cluster-based protocol, which includes distributed cluster formation and rotation of the CH’s role while transmitting data. An enhancement over LEACH protocol called PEGASIS (Power-Efficient Gathering in Sensor Information Systems) was proposed by Lindsey et al. in [13]. PEGASIS is a near optimal chain-based protocol in which, each node communicates only with a close neighbor and takes turns transmitting to the base station, thus, reducing the amount of energy spent per round. The protocols presented in [12] and [13] assume that the memory capacity of the sensor nodes is not limited.
1.2. Our Contribution
We consider a WSN of p stations which contains n items, each station has initially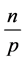 
items. We propose an energy efficient hierarchical permutation routing protocol which performs in 4 stages. The first stage is devoted to the clustering of the network into disjoint cliques where a CH is elected [4]. The second stage is the transformation of cliques obtained after the previous stage in a hierarchy of cliques using [10]. The third stage is allocated to the routing of external items toward their directed clique. Finally, in each clique, we route the internal items to their destination. We show that according to certain parameters, each station has a memory complexity of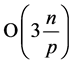 
The remainder of this paper is organized as follow: in Section 2, we present the new hierarchical permutation routing protocol for WSNs. Section 3 deals with some experimental results. A conclusion with open problems ends the paper (Section 4).
2. New Hierarchical Permutation Routing Protocol for Wireless Sensors Network
2.1. Prerequisites
In order to properly run this protocol, it is important to define certain bases. At first, consider that the network has p stations, each of them stores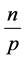 
items and has a unique 
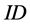between 1 and p. Again, we consider that k channels of communication are available to allow the sensors to communicate. Hence, we write 
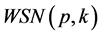and we read wireless sensor network with p stations and k channels. We suppose that n items circulate in the network. Each of the p stations has 
items. Each item is a pair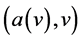 
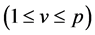. Where 
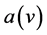is the data to be send to sensor v. Item held by a station may or may not have itself as destination station. Figure 1 illustrates an example of permutation routing in a WSN of 9 stations.
2.2. First Stage: Clustering Procedure in Cliques
Clustering has become a prominent approach to reduce energy consumption in WSNs [14]. In clustering, the network is arranged in clusters of nodes, where each cluster (clique) consists of member sensors, gateways, and a cluster head. The main objective in this first stage is to partition the set of sensors of the network in cliques. Note that clustering can be done in two ways: first, the Node-Centric method consists of choosing the cluster head before choosing clique member’s, and the second method, Cluster-Centric, does the reverse of the first method [8] [15]-[20]. We use the second approach to partition the network in our protocol. Indeed, we will use the protocol presented by Sun et al. in [4] to partition our network. At the end of this, we obtain a number of disjoint cliques within which stations are interconnected to each other, i.e. communication within each clique is one-hop, and each station knows the other’s identity. After clustering, the members of different cliques are responsible for electing the CH. Thiselectionisdone as follows:
1. Each node broadcasts its residual energy with its member’s clique. The sensor with the higher residual energy is then elected as CH.
2. If each of them has the same residual energy, the CH is the one that has the higher ID.
3. After sending items of a particular clique, the station whose identifier is directly below that of the current CH becomes the new CH. If the current CH has the smallest ID, the station with the greater ID will be the new CH. This is doing so on, until all cliques received their destined data.
Figure 2 shows in (a) a network of 10 not-partitioned sensors and (b) the same partitioned network into cliques (3 cliques) using the protocol presented by Sun et al. At the end of this step, all the external items of each clique are known.
2.3. Second Stage: Hierarchical Clustering
At the end of the previous stage, we obtained a set of k cliques (so k CHs). Our goal now is to constitute a hierarchical structure to ensure efficient data routing. For this, we use the protocol presented by Banerjee et al. in [10] . Indeed, the realization of that protocol is made as follows: starting from an initial set of sensors, a multi level covering tree cluster is constructed reassuring that each clique has a number of nodes between x and 2x, where x is an integer value parameter. To apply this, we use the k CHs obtained after the first stage. We set
and we obtain a single cluster [10] . It should be noted that the obtained superclusterhead after the hie-
rarchical clustering knows the identity of all members of the cluster (which actually are the others CHs obtained after the first stage).Figure 3 illustrates a hierarchical clustering (1, 2, 3, 4, 5) with a parameter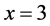 
given,
![]()
Figure 1. Permutation routing in a WSN with p = 9.
using the protocol of Banerjee et al. [10] .
![]()
(a)![]()
(b)
Figure 2. (a) Network of 10 sensors; (b) resulting cluster formation in cliques.
After this stage, the cliques are in a well-defined hierarchy where it remains only to establish the order to transfer data to external cliques.
![]()
Figure 3. An example hybrid clustering: the first stage shows an example of clustering in cliques. The second stage shows the hierarchical clustering of G'.
2.4. Third Stage: Routing the External Items for Each Clique
As in the protocols presented in [8] and [9] , the communication among clusters is made using gateways. In other words, when a station within a clique has the item destined to a particular station in another clique, it sends the item from gateway to gateway until it reaches the gateway of the destination clique. At this time, the latest gateway is charged to send the item at the final destination. Figure 4 illustrates this principle. Moreover, a communication channel is assigned to each clique.
To make it simple, we consider that if x is the number of available channels and k the number of cliques obtained from stage 2, then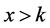 
. Let’s remember that at the end of stage 2, we get a tree that all nodes are CHs and leaves are sensors where one of the CHs is the CH of the tree (superclusterhead).
![]()
Figure 4. An illustration of inter-clique communication.
2.4.1. General Scheduling of Cliques
Our goal in this section is to present the order in which the different cliques of network receive their items. To realize this, we use a similar method like the one presented by Bomgni et al. in [8]. Since the superclusterhead knows the identity of all CHs, it broadcasts the ordered list of ID of the different CH in the tree. After receiving, each CH identifies its position in the list and informs the members of its clique. The notification of members in a clique is done in parallel within the cliques and requires 1 slot. Importantly, no station is awake for more than 1 slot. Hence, this phase requires a total of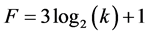 
slots and meanwhile all stations involved remain awake for up to 
slots.
2.4.2. Identifying and Scheduling Cliques That Have Items in Direction of the Clique i
Phase 1: sending the list of members of the clique i to superclusterhead
The communication within cliques constructed in the first stage is one-hop, i.e. all stations are aware of other stations in the clique including the cluster head. The CH sends the list of members of its clique to superclusterhead. Therefore, this phase requires the contribution of different CHs and gateways concerned, i.e., all other stations are asleep during this phase. CH of original clique and the superclusterhead remain awake at most 1 slot. However, the other CHs and relevant gate ways remain awake during 2 slots. One slot to receive the list and the other to retransmit. Thus, each node contributing in this phase remains awake for up to 2 slots. Communication between two cliques requires a maximum of 3 slots. One to move from one station in the clique to the gateway, another one from the gateway to another gateway and the last to move from the gateway to the corresponding station in the clique destined. The time used by the CH to send the list of its neighbors to the farthest clique is equal to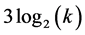 
slots in the worst case. Due to the fact that all the cliques must receive their items and that the super clique does not transmit, this step is performed 
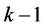times for all the other cliques. It results to a complexity of 
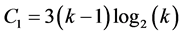slots to complete this phase. With no station being awake for more than 
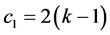slots.
Phase 2: Broadcasting the members’ list of clique i to the other cliques
Using the communication channels allocated to its son’s clique in the tree, the superclusterhead broadcasts the list of members of the clique i. After receiving this list, the CHs record and retransmit it to its sons CHs using their assigned channels. The process is repeated until the leaves receive the list. There is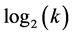 
cliques in the path from the super clique to the deepest clique. The operation described here is realized in parallel on all the branches of the tree and requires 
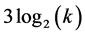slots for completion. During this phase, each cluster head or gateway involved needs to be awake for at most 2 slots, except the superclusterhead which only awakes to send the list and the CHs of leaves that only wake up to receive the list in 1 slot. Then, the members’ transmission of all the k cliques in the network requires 
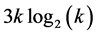time slots. Finally, this phase takes 
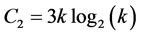time slots, with no station being awake for more than 
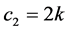slots.
Phase 3: Identifying the items in destination to clique i among different cliques
The goal in this phase is to determine the number of items that different cliques have in destination to clique i. Remember that in the previous phase, the stations of different cliques have the list of stations of the clique i. Since each item to convey is the pair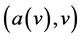 
, stations know whether the items in possession are destined to clique i or not. This is done using the reservation protocol presented by Nakano et al. [6]. After the request of CH, the station with the lowest number wakes up at the first slot to broadcast 
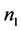in the reserved channel of the clique, which represent the number of item that it has in the destination of clique i. Then, all the other stations are asleep.
In the next slot, the second station with the lowest ID in the clique awakes to receive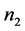 
and then compute the sum 
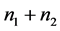and broadcasts the result in the reserved channel of the clique; and during this time, it is the only station awake. The process continues up to the station with the greatest ID. Let 
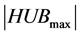being the number of stations in the clique with maximum size. The previous process continues up to the slot 
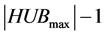, where the station with the greatest number must awake to receive 
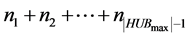. It therefore computes the sum 
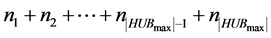and broadcast the result to all the other stations of the clique. Then, with the last diffusion, this operation takes a total of 
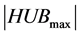slots and no station is awake for more than 3 slots. One slot for the first reception of the sum, another for transmission, and the last one slot to receive the total number of items that the clique has toward the clique i. After this step, each station knows when it will wake up to forward its items. Especially, the station l must awake to the time slot 
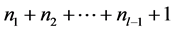46 . This operation is executed 
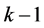times (the clique i is excluded from the process). Thus, this phase is realized in 
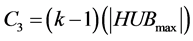times slot, while each station is awake for at most 
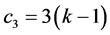slots.
Phase 4: Scheduling the cliques to transfert the items to the clique i
Previously, all stations of different cliques know the number of items destined to the clique i. The goal in this phase is to order the cliques hierarchically so that in different cliques, stations wake up at the right time to receive items from the lowest level and directed to the clique i, after which they broadcast these items to the next level and then go into sleep mode. In the first slot, CHs in leave's cliques wake up and send in the reserved channel of their clique, the number of items that it has in destination to clique i (that is, in the tree obtained in 2.3, each parent node listening over its child channel). After 3 slots, the CHs of the parents’ cliques wake up and receive the numbers sent by their sons, and each of them computes the sum of these numbers. Meanwhile, all other stations not involved in the operation are asleep. That operation unfolds continuously, until the superclusterhead receives the number of items that all cliques except the clique i has in destination to clique i. Since different channels are used for the ascent information in the tree, it comes to superclusterhead in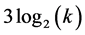 
slots for the most remote cliques. During this, each station involved remains awake for at most 2 slots. Overall, this phase takes 
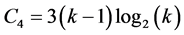times slots, and each station involved remains awake for 
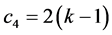slots at most.
Lemma 1
Globally, the scheduling and identifying of cliques that have items directed to the clique i require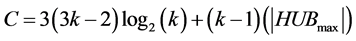 
times slots to run. Each station involved in this phase remains awake for 
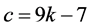slots at most.
Proof: The proof of this result is trivial. In fact, the phase 1 of this step requires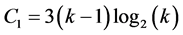 
slots and 
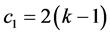awaking slots for stations involved. Phase 2 requires 
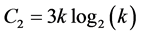times slots and 
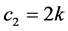awaking slots for stations involved. Phase 3 requires 
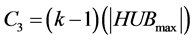slots and 
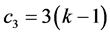awaking slot for stations involved. Finally, phase 4 requires 
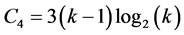slots to complete and 
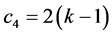awaking slots for the stations involved. Whereby, computing 
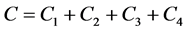and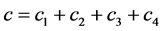 
, we have the result.
2.4.3. Sending External Items Identified in the Tree to the Clique i Using the Cyclic Reception Technique
All the stations in different cliques, know the exact number of item that must be broadcast from their clique to clique i at the end of the previous step. The goal now, is firstly to send all items destined to the clique i in the super clique. Then, secondly to send these items to clique i. Let us clarify these phases.
Phase 1: Broadcast of items destined to clique i to the super clique
Our job in this phase is to forward the items destined to the clique i to the super clique. Remember that at the end of phase 3 (2.4.2), each station knows the exact time that it will wakes up to forward items of clique i. Particularly, the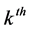 
station of the clique must wakes up to the time slot ![]()
to begin its transmission. Where t is the number of slots that the protocol has already consumed and ![]()
are the numbers of items held by ![]()
number of stations less than k in the clique.
1) Transfer clique i items to the clique of upper level in the tree
2.5. Fourth Stage: Local Broadcasts in Cliques
The pseudo-code of our protocol is as follows (see Figure 5).
Let p sensors in a multi-hop sensor network ![]()
with n items pretitled on it. Without clustering broadcast slots, the permutation routing problem can be solved in ![]()
time slot in the worst case with no station being awake for more than ![]()
slots where![]()
.
![]()
Figure 5. Tree based distributed permutation routing protocol multi hop WSN.
Proof: By summing the results of both lemmas, the time required for internal routing in each clique and the time required for the general scheduling of the cliques, we obtain the result. Indeed, ![]()
and![]()
.
Proof: The proof of this theorem is made as follows:
1) Before the running of the protocol, it is assume that each station has in his internal memory a total of![]()
.
2) During the protocol process, the worst case occur when on the path from the super clique to the clique of maximum number of stations![]()
, items have to pass throw the clique of minimum number of stations![]()
. The total number of items destinate to clique ![]()
is![]()
. Thus, each station of the clique ![]()
must store ![]()
items. According to our hypothesis![]()
, we obtain![]()
. Hence, it is concluded that the memory allocated for routing items in different stations is at most![]()
.
To obtain the maximal memory capacity of each station in the network, we just have to sum the size of the memory for its own items
![]()
and the memory size for routing items
![]()
. Therefore we obtain
![]()
.
3. Simulation Results
In this section, we present the simulation results that we achieved. These simulations were performed in a desktop (Core i7.32 Go RAM, Ubuntu 14.04 LTS) with NS-2.35 and Java Environments. Our main problem has been to establish suitable experimental conditions. We assume that nodes are static and they have the same transmission radius. The experiments take place in a geographic square area of side L. The presented curves are the average of 100 experiments. We made the common assumption that two nodes are neighbors if and only if their Euclidian distance is less than 1 km. The nodes are in a square of 2 km side. In our implementation, the MAC layer is managed in such a way that a node can only receive one message at a time with the number of items sets to 1000.
3.1. Evolution of Sensor’s Energy
The energetic model we use is similar to the one in [13],
![]()
where ![]()
and ![]()
are respectively the energy used for the transmissions and the receptions of items in the network. The energy dissipated by the transmitter, the amplifier and the receiver are respectively expressed by ![]()
and ![]()
. Moreover, d is the Euclidian distance between nodes, N is the energy parameter mitigation ( ![]()
) and n represents the number of items. Thus, based on this model, we value ![]()
to ![]()
and ![]()
to ![]()
with initial energy of sensors to ![]()
and then, we have the Figure 6. This figure is the one which represents communication between two nodes. The curve's energy dissipate while transmitting items to that of the items sender, and the curve of the energy waste while receiving items is that of the receiver node.
3.2. Average Number of Cliques
Figure 7 represents the evolution of the average number of cliques based on the number of nodes of the network. We randomly generate a graph with the labels on the nodes. Then, we partition the previous graph using the protocol of Sun et al. [4] and therefore we get the number of cliques.
3.3. Comparing Our Protocol to That of Lakhlef et al. [7] and That of Bomgni et al. [3]
In the Table 1, we did a comparative study of our protocol to those presented by Bomgni et al. [8] and by Lakhlef et al. [9]. From this table, it is clear that the awaking time taken by our protocol is less than that presented in [8] and [9]. For instance, for ![]()
and ![]()
, the sensors stay awake during 18203881 slots in our protocol, while in the protocols of Bomgni et al. and Lakhlef et al., the sensors stay awake during 19006435 and 46454931 slots respectively. In addition to the awaking time which is better for our protocol, on can noted that
![]()
Table 1. Comparing the time used by our protocol to that of Lakhlef et al. and that of Bomgni et al.
our protocol is executed in consideration of the different memory sizes of sensors’ network that is about![]()
,
in contrast to those presented in [8] and [9] where the memory size of the sensors are infinite.
4. Conclusion and Open Problems
However, several open problems remain. In our future work, we plan to study fault tolerance, which guarantees that normal stations receive in a finite time, the items destined to them. We also, plan to secure this protocol to prevent malicious intrusions. It would also be interesting to see how to mitigate the constraint ![]()
.