Valuation of European Call Options via the Fast Fourier Transform and the Improved Mellin Transform

Sunday Emmanuel Fadugba¹, Chuma Raphael Nwozo^2*

¹Department of Mathematical Sciences, Ekiti State University, Ado Ekiti, Nigeria.
²Department of Mathematics, University of Ibadan, Ibadan, Nigeria.

DOI: 10.4236/jmf.2016.62028                

Abstract

This paper considers the valuation of European call options via the fast Fourier transform and the improved Mellin transform. The Fourier valuation techniques and Fourier inversion methods for density calculations add a versatile tool to the set of advanced techniques for pricing and management of financial derivatives. The Fast Fourier transform is a numerical approach for pricing options which utilizes the characteristic function of the underlying instrument’s price process. The Mellin transform has the ability to reduce complicated functions by realization of its many properties. Mellin’s transformation is closely related to an extended form of other popular transforms, particularly the Laplace transform and the Fourier transform. We consider the fast Fourier transform for the valuation of European call options. We also extend a framework based on the Mellin transforms and show how to modify the method to value European call options. We obtain a new integral equation to determine the price of European call by means of the improved Mellin transform. We show that our integral equation for the price of the European call option reduces to the Black-Scholes-Merton formula. The numerical results show that the tremendous speed of the fast Fourier transform allows option prices for a huge number of strikes to be evaluated very rapidly but the damping factor or the integrability parameter must be carefully chosen since it controls the intensity of the fluctuations and the magnitude of the functional values. The improved Mellin transform is more accurate than the fast Fourier transform, converges faster to the Black- Scholes-Merton model, provides accurate comparable prices and the approach can be regarded as a good alternative to existing methods for the valuation of European call option on a dividend paying stock.

Keywords

Black-Scholes Partial Differential Equation, European Call Option, Fast Fourier Transform, Improved Mellin Transform, Mellin Transform

Received 28 March 2016; accepted 28 May 2016; published 31 May 2016

1. Introduction

In the past decades, option pricing has become one of the major areas in modern financial theory and practice. Since the introduction of the celebrated Black-Scholes option-pricing model, which assumes that the underlying stock price follows a geometric Brownian motion (GBM), there is an explosive growth in trading activities on derivatives in the worldwide financial markets [1] . [2] developed a fast Fourier method to compute option prices for a whole range of strikes. This method makes use of the characteristic function of the underlying asset price. The use of the fast Fourier transform method is motivated by the following reasons: the algorithm has speed advantage. This enables the Fourier transform algorithm to calculate prices accurately for a whole range of strikes. The characteristic function of the log-price is known and has a simple form for many models considered in literature while the density is often not known in the closed form. Option values can be calculated numerically by multiplying a payoff function with transition density of an underlying asset, then taking its discounted expectation with respect to an equivalent martingale measure (see [3] and [4] ). This method of martingale pricing is often computed with respect to the space of the asset, despite often posing more challenging. In 2002, [5] pioneered the method of using the Mellin transform to solve the associated Black-Scholes partial differential equation for a European call option. Mellin transforms in option theory were also introduced by [6] . They derived integral representations for the price of European and American basket put options using Mellin transform techniques. [7] derived integral representations for the prices of European and American put options on a basket of two-dividend paying stocks using integral method based on the double Mellin transform. They showed that by the decomposition of the integral equation for the price of American basket put option, the integral equation for the price of European basket put option can be obtained directly. The Mellin transform method for the valuation of the American power put option with non-dividend and dividend yields respectively was considered by [8] . They used the Mellin transform method to derive the integral representations for the price and the free boundary of the American power put option. They also extended their results to derive the free boundary and the fundamental analytic valuation formula for perpetual American power put option. For mathematical backgrounds, sporadic applications of transform methods in financial contexts see [9] - [18] just to mention a few.

In this paper, we consider the valuation of the European call option via the fast Fourier transform and the improved Mellin transform on a dividend paying stock. The rest of the paper is organized as follows. Section 2 presents overview of the Black-Scholes-Merton model. Section 3 considers some fundamental properties of the Fourier transform and the fast Fourier transform method for the valuation of European options. In Section 4, we present the Mellin transform, some basic properties and the application of the improved Mellin transform in the theory of European call option valuation. Section 5 presents some numerical examples and discussion of results. Section 6 concludes the paper.

2. Black-Scholes-Merton-Like Valuation Formula

We consider a market where the underlying asset price 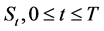is governed by the stochastic differential equation of the form

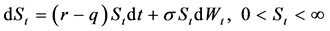(1)

where 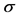is the volatility, r is the riskless interest rate, q is the dividend yield and 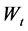is a one-dimensional Wiener process. Standard arbitrage arguments show that any derivative 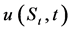written on 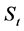must satisfy the partial differential equation [19] .

Theorem 1 [15] : Let 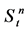denote the price of the underlying asset, 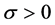the volatility, r the riskless interest rate, n the power of the option, q the dividend yield and 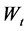the Wiener process. If the underlying price of the asset 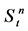follows a random process (Geometric Wiener process) in

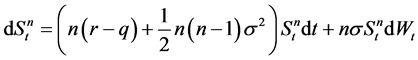(2)

Then the explicit formula for the evolution of the underlying price of the asset is given by

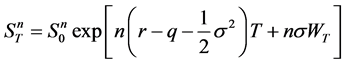(3)

Proof: Let

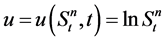(4)

Differentiating (4) we have

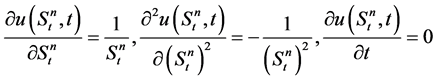(5)

Recall from Ito’s lemma and using (2) for any derivative 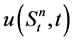we have

(6)

From (2), we can write for

(7)

Substituting (4), (5) and (7) into (6) and rearranging the terms, we have

(8)

Therefore,

(9)

Thus, is a Brownian motion with drift parameter and variance parameter nσ². To derive an explicit formula for the evolution of the stock price, we integrate (9) from 0 to T to obtain

(10)

(11)

Equation (11) can also be written as

(12)

where Z ∼ N(0,1). Therefore the stock dynamic follows a log-normal distribution. For n = 1, (12) becomes

(13)

Equation (13) shows that plain vanilla option follows a log-normal distribution.

Theorem 2: Let the underlying asset price follows a lognormal random walk (geometric Wiener process)

using the Ito’s lemma, under the standard arbitrage argument the Black-Scholes partial differential equation for any derivative on for vanilla power option which pays dividend yield is given by

(14)

Remark 1

1) For n = 1, (14) is known as the regular Black-Scholes-Merton partial differential equation which is given by

(15)

2) If is a vanilla call option, then (15) becomes the Black-Scholes-Merton partial differential equation for a vanilla call option given by

(16)

3) The solution to (16) is obtained as

(17)

where

and is the commutative distribution function for the standard normal distribution

European Options

Definition 1

European is an option that can be exercised only at the expiry date with linear payoff. European option comes in two forms namely European call and put options.

Definition 2

A European call option is an option that can be exercised only at expiry and has a linear payoff given by the difference between underlying asset price at maturity and the exercise price.

Definition 3

A European put option is an option that can be exercised only at expiry and has a linear payoff given by the difference between the exercise price and underlying asset price at maturity.

For a European option on the underlying price of the asset with exercise price K and time to expiry T, we have the payoff for the European call option as

18)

The payoff for the European power put option is given as

(19)

Setting in (15), then we have the Black-Scholes-Merton partial differential equation for the price of European call option given by

(20)

with boundary conditions

(21)

(22)

and final time condition given by

(23)

3. Fast Fourier Transform Method for the Valuation of European Call Options

This section presents some fundamental properties of Fourier transform and the fast Fourier transform method for the valuation of European options. The fast Fourier transform was first proposed by [2] . It ensures that the Fourier transform of the call price exist by the inclusion of a damping factor. Moreover, Fourier inversion can be accomplished by the fast Fourier transform in this case. The tremendous speed of the fast Fourier transform allows option prices for a huge number of strikes to be evaluated very rapidly.

3.1. Fourier Transforms

Definition 4

Suppose is absolutely integrable in, i.e., then the Fourier transform of is defined as

(24)

The Fourier transform is a generalization of the complex Fourier series.

Definition 5

If is square integrable, then the inverse Fourier transform of is defined as

(25)

3.2. Some Fundamental Properties of Fourier Transforms

Let the Fourier transform of be defined as then the following fundamental properties hold as follows:

1) Scaling Property

(26)

2) Shifting/Translation Property

(27)

3) Fourier Transform of Derivatives

(28)

This process can be iterated for the n^th derivative to yield

(29)

Thus, a differentiation converts to multiplication in Fourier space.

4) Convolution Property

(30)

where

(31)

5) Linear Property

(32)

3.3. The Fast Fourier Transforms

The fast Fourier transform (FFT) is proposed by [20] . The fast Fourier transform is an efficient algorithm for computing the discrete Fourier transform of the form;

(33)

where N is typically a power of two. Equation (33) reduces the number of multiplications in the required N summations from an order of to that of, a very considerable reduction. Let p and j be written as binary numbers i.e. and with, then (33) becomes

(34)

The fast Fourier transform can be described by the following three steps as

(35)

Remark 2

[20] showed that it was in fact possible to have the discrete Fourier transform evaluated with arithmetic operations. This algorithm is called the fast Fourier transform. As a matter of fact, ef-

ficient methods for evaluating the discrete Fourier transform have already been devised as long ago as in 1805 by Gauss. However, the world was dormant until 1965. Figure 1 illustrates the huge differences between

and.

The basic idea of the fast Fourier transform is to develop an analytic expression for the Fourier transform of the option price and to get the price by means of Fourier inversion.

By means of a change of variables, it is observed that the Fourier transform bears a striking resemblance to the Laplace and the Mellin transforms. In particular, if denote the two-sided Laplace and Mellin transforms respectively, then we have

3.4. The Characteristic Function in the Domain of the Black-Scholes Model

The dynamics of the stock price in a risk-neutral Black-Scholes world follows geometric Brownian motion with a non-dividend yield is of the form

Utilizing the Ito’s formula we can explicitly solve for;

from which we can see that is lognormally distributed. Hence for the characteristic function of we have that

Figure 1. Huge differences between and.

3.5. Application of the Fast Fourier Transform for the Valuation of European Call Options

The Fourier pricing techniques and Fourier inversion methods for density calculations add a versatile tool to the set of advanced techniques for pricing and management of financial derivatives. The Fast Fourier transform method is a numerical approach for pricing options which utilizes the characteristic function of the underlying instrument’s price process. This approach was introduced by [2] . The Fast Fourier transform method assumes that the characteristic function of the log-price is given analytically.

Consider the valuation of European call option. Let the risk neutral density of be. The characteristic function of the density is given by

(36)

The price of a European call option under the risk-neutral valuation with maturity T and exercise price K denoted by is given by

(37)

where p is the log of the strike price K i.e.

(38)

Substituting (38) into (37) yields

(39)

in which the expectation is taken with respect to some risk-neutral measure. Since

The integral representation given by (39) is not square integrable, i.e. as does not tend to zero for. We consider a modified version of the call price in (39) given by

(40)

Equation (40) is square integrable in p over the entire real line. Using (24) and (25), we have that

(41)

(42)

Substituting (40) into (41) we obtain a new call value in the Fourier transform domain as

(43)

Substituting (43) into (39) we have that

Since for,. Therefore we have that

(44)

where is the characteristic function of the given by (36).

Remark 3

A sufficient condition for to be square-integrable is given by being finite. This is equivalent to. [2] established that if the integrability parameter, the denominator of (44) vanishes when, inducing a singularity in the integrand. Since the fast Fourier transform evaluates the integrand at, the use of the factor is required.

Now, we obtain the desired option price in terms of using Fourier inversion of the form:

(45)

Substituting (44) into (45) yields

(46)

By recognizing that the call price is real (even in real part, odd in imaginary). Due to the condition a, (46) is well defined. After discretizing and using Simpson’s rule, (46) can be computed numerically by means of the fast Fourier transform as:

(47)

where and is the Kronecker delta function defined as

Hence, the integration (46) is an application of the summation (33).

We formalized remark 3 in the following result below.

Theorem 3

Let. The Fourier transform of exists if

Proof: We note that since

where

From (42), we write that

Combining this with completes the proof.

Remark 4

For the Black-Scholes model the integrand in (46) reduces to

(48a)

where

(48b)

From (48b), we can get more fluctuating integrand by increasing any of the parameters. The magnitudes of these fluctuations get larger which can be seen from the exponential term in (48a).

Remark 5

At this point it is unavoidable to comment on the choice of the integrability parameter a. A small value of a is favourable since this reduces both the oscillations and the magnitudes hereof. However choosing a too small can turn the integrand into a sort of impulse function, which is not tractable at all from a numerical integration point of view. This follows from the fact that in the origin, the Black-Scholes integrand in (48a) becomes

(48c)

Taking the limit of (48c) as yields

(48d)

Similarly (48c) tends to infinity as

(48e)

On the other hand, for and by letting, the integrand (48a) becomes:

(48f)

with.

Equation (48f) decreases very fast as a function of v because of the exponential term.

The following result shows how the Black-Scholes integrand attains its maximum at

Theorem 4

Let. The Black-Scholes integrand

(48g)

attains its maximum at, where

Proof: From (48c) we have that

We see that (48c) is equivalent to

(48h)

This follows since

(48i)

where

(48j)

Moreover,

(48k)

Using (48j) and (48k), we have that

This completes the proof.

4. Mellin Transform Method for the Valuation of European Call Options

In this section, we present the Mellin transform, some basic properties and the application of the improved Mellin transform in the theory of option pricing.

4.1. Mellin Transforms

Definition 6

The Mellin transform is a complex valued function defined on a vertical strip in the ω-plane whose boundaries are determined by the asymptotic behaviour of f(x) as x → 0⁺ and x → ∞. The Mellin transform of the function f(x) is defined as

(49)

The function is called the Mellin transform of. In general, the integral does exist only for complex values of such that, where u and v depend on the function to transform. This introduces what is called the strip of definition of the Mellin transform that will be denoted by. In some cases, this strip may be extended to half-plane or

Definition 7

If is an integrable function with fundamental strip, then if c such that and is integrable, the equality

(50)

holds almost everywhere. Moreover, if is continuous, then the equality holds everywhere on.

If is defined on the positive real axis and, then the following properties of the Mellin transform hold.

a) Shifting Property

(51)

b) Scaling Property

(52)

c) The Mellin Transform of Derivatives

(53)

where the symbol is defined for k integer by;

Equations (51) and (53) can be used in various ways to find the effect of linear combination of differential operator such that integers. The most remarkable results are

(54)

where j is a positive integer and.

d) Convolution Property

(55)

4.2. Integral Representation for the Price of European Call Options via the Mellin Transform

We observe that

(56)

the Mellin transform for the call option does not exist and the integral fails to converge. In this paper we use the improved version of the Mellin transform for the valuation of the European call option with the variable change

(57)

With this change the usual notation for the transform is preserved. This is to ensure the Mellin transform of the European call payoff function exists for some fundamental strip. The improved Mellin transform for the price of the European call option is defined as

(58)

Conversely the inversion formula for (58) is given by

(59)

Taking the improved Mellin transform of (20) yields

(60)

Equation (60) becomes

(61)

(62)

Equation (62) is the general solution of (61), with, where is a constant that depends on the final time condition/ terminal condition which is of the form

(63)

where

(64)

Equation (64) is the improved Mellin transform of the final time condition.

Substituting (64) into (63) we have that

(65)

Using (62) and (65), we have that

(66)

Taking the inverse improved Mellin transform of (66), the integral representation for the price of European call option is obtained as

(67)

with, is a constant and.

Theorem 5: The boundary value problem for the Black-Scholes-Merton Equation (20) for the price of the European call option with exercise price K, subject to the boundary condition (23) has a unique solution of the form

(68)

Proof: The differential equation given by (61) of the form

where

can also be written as

(69)

with the final time condition given by

(70)

The solution to (69) is obtained as

(71)

Simplifying (71) further, yields

(72)

where

(73)

Taking the inverse improved Mellin transform of (72), we have that

(74)

Setting

(75)

Equation (74) becomes

(76)

Let

(77)

Using the scaling property (52) and the convolution property (55), we have that

(78)

If we impose the final time condition

(79)

Equation (79) becomes

with

Hence, (68) is established.

Theorem 6: The boundary value problem for the Black-Scholes-Merton equation for the price of the European put option with exercise price K given by

(80)

subject to the boundary condition

(81)

(82)

and final time condition

(83)

has a unique solution of the form

(84)

with

Proof: Using scaling property (52), convolution property (55), the final time condition (83) and the put-call parity. Equation (84) follows from theorem 5.

Theorem 7: The expressions (67), (68) and Black-Scholes-Merton model

(85)

(86)

for the European call option are analytically equivalent.

Proof: From (67) we have that

(87)

where

Simplifying (87) further yields

(88)

with

Now, is the Mellin transform of

(89)

Using equation (7.2.1) in [21] which is of the form

(90)

We get

(91)

By means of convolution property of the Mellin transforms (see [22] ). The price of the European call option becomes

(92)

From (81) we write that

(93)

Combining (79), (92) and (93) we have that

(94)

where

(95)

(96)

(97)

(98)

To evaluate the first and second integrals in (97) and (98), we use the transformations

(99)

and

(100)

respectively.

Finally, we obtain the first and second parts of (94) as

(101)

(102)

where are given by (86).

Substituting (101) and (102) into (94) yields

This completes the proof.

5. Numerical Examples and Discussion of Results

In this section, we present some examples to compare the results obtained by the fast Fourier transform and the improved Mellin transform with the values of the Black-Scholes-Merton model.

Example 1

We consider the pricing of the European call option on a dividend-paying stock via fast Fourier transform and the Mellin transform with the following parameters

in the context of the Black-Scholes-Merton model. The option values, P, absolute error and log absolute error for the two transforms against the values of the Black-Scholes-Merton model are shown in Figures 2-4.

Example 2

We consider the valuation of European call option with Forty-Eight months to go until expiration on the “Standard and Poor’s 500” index (S & P 500), with a current price of $110, a strike price of $100, a continuously compounded interest rate of 5%, a volatility of 35% and varying a constant annual index dividend estimated

at using fast Fourier transform, improved Mellin transform, Monte Carlo method

in the context of the Black-Scholes-Merton model. The influence of dividend yield on the results generated is shown in Figure 5.

Discussion of Results

Figures 2-4 show that the fast Fourier transform and the improved Mellin transform perform better and agree with the values of the Black-Scholes-Merton model. We can also see that the improved Mellin transform provides a close approximation to the Black-Scholes-Merton formula. Figure 5 shows that the values of the improved Mellin transform, Monte Carlo method and the Black-Scholes-Merton model coincide. Also the higher

Figure 2. The comparative result analyses of the fast Fourier transform (FFT) and the Black-Scholes-Merton model (BSM).

Figure 3. The comparative result analyses of the improved Mellin transform (MT) and the Black-Scholes-Merton model (BSM).

Figure 4. The comparative results analysis of the fast Fourier transform (FFT), the improved Mellin transforms (MT) and the Black-Scholes-Merton model (BSM).

Figure 5. The influence of dividend yield on the valuation of European call option via the fast Fourier transform (FFT), the improved Mellin transform (MT), the Monte Carlo method (MC) and the Black-Scholes-Merton model (BSM).

the dividend yield, the smaller the values of the methods. The numerical results show that the tremendous speed of the fast Fourier transform allows option prices for a huge number of strikes to be evaluated very rapidly but the damping factor or the integrability parameter must be carefully chosen since it controls the intensity of the fluctuations and the magnitude of the functional values. The improved Mellin transform provides accurate comparable prices and the approach can be regarded as a good alternative to existing methods.

6. Conclusion

We have considered the fast Fourier transform and the improved Mellin transform for the valuation of the European call option which pays dividend yield. Financial modeling in the area of option pricing involves detailed knowledge about stochastic processes describing the asset payoffs. For sophisticated price dynamics, these are most conveniently characterized through functions in image space. By a mapping of the probability function from spatial domain to the unit circle in the complex plane, expected values of a future payoff are then available in the form of an integral representation. In this paper, we outlined general features of Fourier transform techniques applicable to both the modeling of density functions and European call option pricing. We also consider some properties of the Mellin transform and its applications in the theory of option valuation. To emphasis the generality of our results, we have shown the equivalence of the integral representation for the price of the European call option via the improved Mellin transform to the Black-Scholes-Merton formula. From Figures 2-5, we can see that the improved Mellin transform provides a close approximation to the Black-Scholes-Merton model, more accurate than the fast Fourier transform and it is a good alternative method for the valuation of the European call option on a dividend paying stock.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
[2]	Carr, P. and Madan, D. (1999) Option Valuation Using the Fast Fourier Transform. Journal of Computational Finance, 3, 463-520.
[3]	Musiela, M. and Rutkowski, M. (2006) Martingale Methods in Financial Modelling. Springer, Berlin.
[4]	Duffie, D. (2010) Dynamic Asset Pricing Theory. 3rd Edition, Princeton University Press.
[5]	Cruz-Baez, D.I. and Gonzalez-Rodriguez, J.M. (2002) Semigroup Theory Applied to Options. Journal of Applied Mathematics, 2, 131-139. http://dx.doi.org/10.1155/S1110757X02111041
[6]	Panini, R. and Srivastav, R.P. (2004) Option Pricing with Mellin Transforms. Mathematical and Computer Modelling, 40, 43-56. http://dx.doi.org/10.1016/j.mcm.2004.07.008
[7]	Fadugba, S.E. and Nwozo, C.R. (2015) Integral Representations for the Price of Vanilla Put Options on a Basket of Two-Dividend Paying Stocks. Applied Mathematics, 6, 783-792. http://dx.doi.org/10.4236/am.2015.65074
[8]	Fadugba, S.E. and Nwozo, C.R. (2005) Mellin Transform Method for the Valuation of the American Power Put Option with Non-Dividend and Dividend Yields. Journal of Mathematical Finance, 5, 249-272. http://dx.doi.org/10.4236/jmf.2015.53023
[9]	McKean, H. (1965) Appendix: A Free Boundary Problem for the Heat Equation Arising from a Problem in Mathematical Economics. Industrial Management Review, 6, 32-39.
[10]	Buser, S.A. (1986) LaPlace Transforms as Present Value Rules: A Note. The Journal of Finance, 41, 243-247. http://dx.doi.org/10.1111/j.1540-6261.1986.tb04502.x
[11]	Jodar, L.P., Sevilla-Peris, P., Cortes, J.C. and Sala, R. (2002) A New Direct Method for Solving the Black-Scholes Equation. Applied Mathematics Letters, 18, 29-32. http://dx.doi.org/10.1016/j.aml.2002.12.016
[12]	Bakshi, G. and Madan, D. (2000) Spanning and Derivative Security Valuation. Journal of Financial Economics, 55, 205-238. http://dx.doi.org/10.1016/S0304-405X(99)00050-1
[13]	Frontczak, R. (2013) Simple Analytical Approximations for the Critical Stock Price of American Options. Working Pa per. http://ssrn.com//abstract=2227626 http://dx.doi.org/10.2139/ssrn.2227626
[14]	AlAzemi, F., AlAzemi, A. and Boyadjiev, L. (2014) Mellin Transform Method for Solving the Black-Scholes Equations. International Journal of Pure and Applied Mathematics, 97, 287-301. http://dx.doi.org/10.12732/ijpam.v97i3.3
[15]	Nwozo, C.R. and Fadugba, S.E. (2014) Mellin Transform Method for the Valuation of Some Vanilla Power Options with Non-Dividend Yield. International Journal of Pure and Applied Mathematics, 96, 79-104. http://dx.doi.org/10.12732/ijpam.v96i1.7
[16]	Nwozo, C.R. and Fadugba, S.E. (2014) Performance Measure of Laplace Transforms for Pricing Path Dependent Options. International Journal of Pure and Applied Mathematics, 94, 175-197. http://dx.doi.org/10.12732/ijpam.v94i2.5
[17]	Zhu, J. (2000) Modular Pricing of Options. An Application of Fourier Analysis. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-04309-7
[18]	Nwozo, C.R. and Fadugba, S.E. (2015) On Two Transform Methods for the Valuation of Contingent Claims. Journal of Mathematical Finance, 5, 88-112. http://dx.doi.org/10.4236/jmf.2015.52009
[19]	Wilmott, P., Dewynne, J. and Howison, S. (1993) Option Pricing, Mathematical Models and Computation. Oxford Financial Press, Oxford.
[20]	Cooley, J.W. and Turkey, J.W. (1965) An Algorithm for the Machine Computation of the Complex Fourier Series. Mathematics of Computation, 19, 297-301. http://dx.doi.org/10.1090/S0025-5718-1965-0178586-1
[21]	Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. (1954) Tables of Integral Transforms. Vol. 1-2, McGraw-Hill, New York.
[22]	Sneddon, I. (1972) The Use of Integral Transforms. McGraw-Hill, New York.