A Pure Strategy Nash Equilibrium Bertrand Game with Strictly Positive Profits

Yongjian Pu, Lei Zhu

School of Economics and Business Administration, Chongqing University, Chongqing, China.

DOI: 10.4236/jss.2016.43009                

Abstract

This paper explores the existence of pure strategy Nash equilibrium of a Bertrand game with strictly positive profits. We show that when fixed cost is small enough, there always exists pure strategy Nash equilibrium with strictly positive profits if firms have quadratic cost functions and linear demand curve.

Keywords

Bertrand Game, Nash Equilibrium, Pure Strategy, Strictly Positive Profits

1. Introduction

The Bertrand paradox indicates that zero profits are earned if two identical firms produce homogeneous products in a duopoly market. There has been some work discussing the existence of mixed-strategy Nash equilibrium of a Bertrand game with positive profits [1], [2]. However, both [1] and [2] adopted impractical assumptions. In [1], the monopoly profit tends to infinity as the price tends to monopoly price. Moreover, [1] assumed that when several firms set the same lowest price, the profit of each firm is the monopoly profit divided by the number of the firms setting the same lowest price. In [2], the revenue tends to infinity as the price tends to infinity. In [3], the existence of pure strategy Nash equilibrium of a Bertrand game with positive profits is analyzed. In [4], the case was extended to discontinuous demand scenario, but the fixed cost was assumed to be zero.

2. Model

2.1. Assumptions

・ Cost Function

A1: There are two identical firms competing in the market. They produce homogeneous products and the cost function is:

.

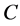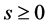, and are total cost, quantity and fixed cost; and are constants.

・ Demand Curve

A2: Suppose that price and demand satisfy a linear relationship:

.

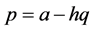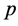and are price and demand; and are constants. It requires that:

.

・ Market Share

A3: Since the two firms produce homogeneous products, any one setting a lower price will own the entire market. If the two firms set the same price, they split the demand evenly.

2.2. Critical Prices

Let denote the monopoly profit function of price, the profit function of each firm when they set the same price: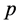

;

.

Then we derive three critical prices to determine the Nash equilibrium price interval.

・ Zero Profit Price

Let, we have:

.

It requires that:. Otherwise, the profit is always negative.

・ Maximum Profit Price

Let, we have:

;

.

・ Identical Profit Price

Let, we have:

.

3. Discussion

3.1. Preliminaries

Lemma 1. If, then; else.

Proof.. Note that by A2.

Lemma 2. If, is continuous at, then there exists, such that , when.

Proof. Let. By the continuity of at, for any, there exists, such that when. Then we have:

Lemma 3..

Proof.. Note that by A2.

Lemma 4. If, then.

Proof.

Lemma 5. If, then; then.

Proof..

3.2. Conclusions

Theorem. A Bertrand game satisfying assumptions A1 through A3 has Nash equilibria with strictly positive profits if, where and are price strategies of the firms.

Proof. First of all, we claim that is an upper bound by that any price above is not a Nash equilibrium. Suppose, by lemma 1 and lemma 2, the second firm has an incentive to earn more profit by undercutting its competitor a little bit:. The first firm would react the same given that. This process does not come to an end until. Next, we suppose, then the best response of the second firm is. If, the second firm loses the whole market. If, the second firm owns the whole market, but earns less profit than splitting the market evenly with the first firm by lemma 1 and lemma

3:. Note that is an increasing function when. Finally, any

price below leads to a negative profit. As a consequence, to earn strictly positive profits, it suffices to let. By lemma 4, the theorem holds.

Proposition: In a Bertrand game satisfying assumptions A1 through A3 with strictly positive profits, the price strategies of the two firms to earn maximum profits are 1), if; 2), otherwise.

Proof. It follows from the theorem and lemma 5.

Acknowledgements

This work was supported by the Ministry of Science and Technology of the People’s Republic of China under National Science and Technology Supporting Project 2015BAG10B00 “Research and Demonstration of Electric Vehicle Time Sharing Rental Pattern and Supporting Technologies in Mountainous City”.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Baye, M.R. and Morgan, J. (1999) A Folk Theorem for One-Shot Bertrand Games. Economics Letters, 65, 59-65. http://dx.doi.org/10.1016/S0165-1765(99)00118-4
[2]	Kaplan, T.R. and Wettstein, D. (2000) The Possibility of Mixed-Strategy Equilibria with Constant-Returns-to-Scale Technology under Bertrand Competition. Spanish Economic Review, 2, 65-71. http://dx.doi.org/10.1007/s101080050018
[3]	Dastidar, K.G. (1995) On the Existence of Pure Strategy Bertrand Equilibrium. Economic Theory, 5, 19-32. http://dx.doi.org/10.1007/BF01213642
[4]	Bagh, A. (2010) Pure Strategy Equilibria in Bertrand Games with Discontinuous Demand and Asymmetric Tie-break- ing Rules. Economics Letters, 108, 277-279. http://dx.doi.org/10.1016/j.econlet.2010.05.016