On α-Weyl Operators

Slaviša V. Djordjević^*, Fernando Hernández-Díaz

Facultad de Ciencias Físico-Matemáticas, BUAP Río Verde, Puebla, México.

DOI: 10.4236/apm.2016.63011                

Abstract

The purpose of this article is to present Schechter’s manner to introduce α-Wayl operators and compare this definition with another one given by Yadav and Arora. Moreover, we introduce generalized Weyl operator in the way that we keep many properties of the class of Weyl operators.

Keywords

Fredholm Operators, α-Closed Subspaces, α-Weyl Operators

Received 23 December 2015; accepted 21 February 2016; published 26 February 2016

1. Introduction

Let H be a (complex) Hilbert space and denote the Hilbert dimension of the space H, where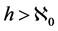. Then any nonzero proper closed two-side ideal in is the form

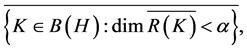
for some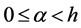. Denote this ideal with 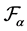(For more details see [1] ). In the case when 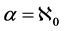(cardinality of the natural numbers), we have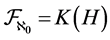, the ideal of all compact operators. We denote the kernel

of an operator by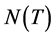, , and, where denotes

the rank of an operator. Using duality we have.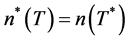

One of the classical (Atkinson) characterization of Fredholm operators is invertibility in Calkin algebra, i.e. 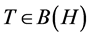is a Fredholm operator if and only if 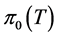is invertible in if and only if is invertible in, where and are natural homomorphisms from in the cocients and respectively ([2] , Theorem 3.2.8). Another way to introduce Fredholm ope- rators is using the dimensions of the kernel and the codimension of the rang of an operator: is called an upper semi-Fredholm operator if and is closed, and T is called lower semi-Fredholm if (consequently the range of T is closed). The set of all upper (respectively, lower) semi-Fredholm operators will be denoted by (respectively). The set of all semi-Fredholm operators is defined by and the set of all Fredholm operators is defined by. The index of a semi-Fredholm operator is defined as and the Weyl operators with. The Weyl operator still conserves one of the basic properties for the operators between finite dimensional spaces: Fredholm alternative. Moreover, with some extra conditions (like finite ascent or descent), such operators have very nice property: there are Drazin invertible (For more details about generalized invertibility we suggest [3] ). Now, the natural question appears: it is necessary to observe only finite dimensional situation for kernel, or co-dimension of range, or ascent and descent, etc.

We can find the very first investigation in this direction in the works of G. Edgar, J. Ernest and S. G. Lee. In papers [4] [5] , they introduce the definition of an a-closed subspace which allowed them to give a new definition of an a-Fredholm operator. Accordingly ([4] , Definition 2.7), is an a-Fredholm operator, , if and is a-closed.

The main results of the paper are present in remaining two sections. In the next section we define b-index of an a-Fredholm operator, for, which we use in definition of a-Weyl operator and a-Weyl spectrum (Definition 2). In the theorems 3, 5 and 7 we give some basic properties of such operators. In the last section we define the generalized Weyl operator in the way that we widespread the definition given by D.S. Djordjević in [12] . The new class of the generalized Weyl operator conserves many properties of the class of Weyl operators (see Theorem 9).

2. a-Weyl Operators

For Hilbert spaces, L. A Coburn, in [13] , defined the Weyl spectrum of an operator as

where denoted usual spectrum of.

On the other hand, in the same year, M. Schechter (see [14] ) defined the Weyl spectrum of T by

S. K. Berberian in [15] established the equivalence between both definitions and we will use to denote the Weyl spectrum.

The notion of Fredholm operators can be extended to an arbitrary dimension (less then the dimension of the space H) of the null space of T and using the a-closedness. In this way, in [4] , G. Edgar, J. Ernest and S. G. Lee defined the a-Fredholm operator, for some, like an operator that has a-closed range and both of and are less than a. It is worth mentioning that a subset K in H is a-closed if there exists a closed subset such that and.

If denotes the approximate nullity of T (for the definition and basic property see [4] ), then, by ([4] , Theorem 2.6) and ([16] , Theorem 3.1), we have nice (Atkison type) characterization for an a-Fredholm operator.

Theorem 1. Let T be an operator on and a be a cardinal number such that. Then the following conditions are equivalent:

1) T is an a- Fredholm operator (in notation).

2).

3) T is invertible modulo.

For more properties of a-Fredholm operators we specially refer to [4] [16] [17] .

Later, Yadav and Arora, in [11] , for non separable Hilbert spaces, defined the Weyl spectrum of wight a for some operator as

Let be an a-Fredholm operator, , then we can extend the definition of index, for all, using slightly modification of definition in [18] (for more details see [16] ):

In the way of Schechter definition of the Weyl operators, we defined a-Weyl operators next.

Definition 2. For an operator we say that it is a-Weyl operator, for some cardinal a, , if T is an a-Fredholm operator with, for all cardinals b,.

We can define the a-Weyl spectrum in (one of the usual) way(s):

Now arise natural question about equivalency of two ways of definition of a-Weyl spectrums. It is easy to see that

The next theorem gives us the answer for all a,.

Theorem 3. Let T be an operator on and let a be a cardinal number such that. Then.

Proof. If, then the results follows from the classical Fredholm theory.

Let and. Then there exists a such that is invertible. Hence, is an (invertible) a-Fredholm operator with, for all. Since

,

by ([17] , Theorem 2.6) and ([18] , Corollary 1), is an a-Fredholm operator and, for all, i.e..

Let. Then is an a-Fredholm operator and, for every cardinal, we have. In this case we have that. If, then results follows by the properties of (usual) Weyl spectrum.

Let. Suppose that has closed range. Let i be an isometry from onto (that are same dimension) and let is definite by:

In the same decomposition of H we can present in the way:

where is invertible. It is easy to see that the operator is invertible and.

In the case when is a-Fredholm operator with no closed range, by ([4] , Theorem 2.6), for each small enough, there exists a closed subspace of H that contains and for any non-zero vector in. Moreover, , for every, and

.

Additionally, by ([16] , Lemma 4.8),. Since is

bounded below in, follows that is a closed subspace that together with

implies that is an invertible operator. Set

where is an arbitrary isomorphism between g-dimensional (closed sub)spaces. Then is an invertible operator and. To proof last, let

then

and that implies. Hence, is an invertible operator, i.e..

Remark 4. (1) In the future, we will use the notation for the a-Weyl spectrum of T.

(2) In the case when, if we slightly modificated the proof of Theorem 3 with additional condition that, we can see that an a-Weyl operator that is not invertible can be approximated (in the norm) with an invertible operator, i.e. its belong to.

Let, then we can define family of a-Weyl operators, in notation, like:

Theorem 5. Let T be an operator on and let a be a cardinal number such that. Then the following conditions are equivalent:

1);

2) and is a-closed;

3).

Proof. (1) Û (2) follows directly from definition of a-Fredholm operator and definition of.

(2) Û (3) follows from ([4] , Theorem 2.6) and ([16] , Theorem 3.1 and Lemma 4.8).

Remark 6. Any of equivalent condition (1)-(3) of Theorem 5 implies that there exists a closed subspaces M and N of H such that, and. Really, let

.

Then, by ([16] , p. 221), there exists a such that, for any. For some fix, let from definition of for T and N we define in similar way, only using operator.

Theorem 7. Let T be an operator on and let a be a cardinal number such that.

1) is open.

2) If, then.

3) If and, then.

Proof. (1) Let. By Theorem 5 (3), and, for small enough, there exists a closed subspace such that

for all and

Moreover, , where is a closed subspace of H. For more details see ([16] , pp. 220-221).

Let such that. Suppose that there is a non-zero. Then

, which is contradictory with selection of subspace. Hence, and. Also, by, we have.

Moreover, S is bounded below on,

that implies is a closed subspace contained in. Using the matrix representation of S in respect

of decomposition and, we get

and

which implies is an a-closed subspace.

Hence, for any such that, is an a-closed subspace and, i.e..

(2) Let, then. By Theorem 3, there exists a such that. Then,

i.e..

(3) By Theorem 3 and ([18] , Corollary 1) (also see ([11] , Theorem 3)).

3. Generalized Weyl Operators

Let and be cardinality such that. By ([17] , Renmark 3.2), we have that. Moreover, it is easy to see that, if for some, , for all, then, for all, i.e..

Definition 8. The set of the generalized Weyl operator, in notation, is

In [12] , D. S. Djordjević defines the class of generalized Weyl operator like

Since a closed subspace in H is a-closed, for any cardinal a, , and implies that, we have that. Besides that, the properties of are more similar to than those of. The set is not open, but, by Theorem 7, the set is open (like). Similar, the set is closed in respect of composition of operators (by Theorem 7 (2)) and compact perturbations. Hence, we have next theorem that generalizes results from [12] .

Theorem 9. (1) If, then.

(2) If and, then.

(3) is open in.

Acknowledgements

Research of the authors is funded by the CONACYT grant CB-2011-168109-F. This support is greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Luft, E. (1968) The Two-Sided Closed Ideals of the Algebra of Bounded Linear Operators of a Hilbert Space. Czechoslovak Mathematical Journal, 18, 595-605.
[2]	Caradus, S.R., Pfaffenberger, W.E. and Yood. B. (1974) Calkin Algebras and Algebras of Operators on Banach Spaces. Marcel Dekker, Inc., New York.
[3]	Djordjevic, D.S. and Rakocevic, V. (2008) Lectures on Generalized Inverses. Faculty of Sciences and Mathematics, University of Nis, Nis.
[4]	Edgar, G., Ernest, J. and Lee, S.G. (1972) Weighing Operator Spectra. Indiana University Mathematics Journal, 21, 61-80. http://dx.doi.org/10.1512/iumj.1972.21.21005
[5]	Ernest, J. (1972) Left Invertibility of Closed Operators Modulo an α-Compact Operator. Tohoku Mathematical Journal, 24, 529-537. http://dx.doi.org/10.2748/tmj/1178241443
[6]	Arora, S.C. and Dharmarha, P. (2006) On Weighted Weyl Spectrum, II. Bulletin of the Korean Mathematical Society, 43, 715-722. http://dx.doi.org/10.4134/BKMS.2006.43.4.715
[7]	Arora, S.C. and Dharmarha, P. (2007) Operators Satisfying . International Journal of Pure and Applied Mathematics, 34, 197-202.
[8]	Arora, S.C. and Dharmarha, P. (2007) On Joint Weighted Spectrum. Bulletin of Calcutta Mathematical Society, 99, 539-546.
[9]	Dharmarha, P. (2009) A Study of Weighted Weyl Spectra of Operators. Ph.D. Dissertation, Department of Mathematics, University of Delhi, New Delhi.
[10]	Dharmarha, P. (2007) Weighted Weyl Spectrum. Ganita, 58, 67-74.
[11]	Yadav, B.S. and Arora, S.C. (1980) A Generalization of Weyl’s Spectrum. Glasnik Mathematicki, 15, 315-319.
[12]	Djordjevic, D.S. (2001) On Generalized Weyl Operators. Proceedings of the American Mathematical Society, 130, 81-84. http://dx.doi.org/10.1090/S0002-9939-01-06081-6
[13]	Coburn, L.A. (1966) Weyl’s Theorem for Nonnormal Operators. The Michigan Mathematical Journal, 13, 285-288. http://dx.doi.org/10.1307/mmj/1031732778
[14]	Schechter, M. (1965) Invariance of the Essential Spectrum. Bulletin of the American Mathematical Society, 71, 365-367. http://dx.doi.org/10.1090/S0002-9904-1965-11296-4
[15]	Berberian, S. (1971) The Weyl Spectrum of an Operator. Indiana University Mathematics Journal, 20, 529-544. http://dx.doi.org/10.1512/iumj.1971.20.20044
[16]	Burlando, L. (1999) Approximation by Semi-Fredholm and Semi-α-Fredholm Operators in Hilbert Spaces of Arbitrary Dimension. Acta Scientiarum Mathematicarum (Szeged), 65, 217-275.
[17]	Hernández-Díaz, F. and Djordjevic, S.V. (2016) α-Fredholm Spectrum of Hilbert Space Operators. Journal of the Indian Math. Soc.
[18]	Coburn, L.A. and Lebow, A. (1968) Components of Invertible Elements in Quotient Algebras of Operators. Transactions of the American Mathematical Society, 130, 359-365. http://dx.doi.org/10.1090/S0002-9947-1968-0223901-2