Atomic epn(ep) Spin Models and Spectral Lines

Daekyoum Kim¹, Baik-Hyon Ha²

¹Kwongmyoung-Si, Kyoungki-Do, South Korea.
²Emeritus, Chemical Engineering Department, Hanyang University, Seoul, South Korea.

DOI: 10.4236/ajac.2015.613098                

Abstract

We confirmed that how many kinds of epn spins the atoms have by calculating heat capacity of metals according to energy levels in the previous reference. To know more the spin models of epn of hydrogen and helium are imagined and their line spectra are counted. And the explanation of interference is discussed. Gas atoms make line spectra by optical interference. Solid atoms make them by exciting the lowest epns of their cluster first. They all make s, p energy orbit. One axis is composed of two epns. 1s or 2s of atoms except for lithium generally makes the symmetric axis. When each energy level is filled up by epns, these are symmetrically paired first. The atoms which fit the number of line spectra correctly by optical interference are hydrogen and helium. By counting the number of alignments of epns spins within the cluster, the atoms which fit the number of line spectra correctly are lithium, beryllium and phosphorus. The number of line spectra of the rest atoms which we have counted approaches the experimented numbers approximately, not correctly.

Keywords

Atomic Model, Atomic Cluster, Spectral Lines, Resonance

Received 18 September 2015; accepted 15 December 2015; published 18 December 2015

1. Introduction

Humphreys [1] -[3] says that we can explain the line spectra through interferometric measurement on some gas atoms. The line spectra of atoms come out much more than their atomic number. Until now one electronic atomic model is solved through Schrödinger’s equation, and then its energy levels are used on interpreting the line spectra.

Hence 4 kinds of spin energy level for each epn (one electron + one proton + one neutron) with one additional energy level in the previous reference [4] are assumed and used on explaining the heat capacity of metals according to energy levels without any problems. The arrangement of spins of each epn (or ep) is that the proton (+neutron) is situated in the inside of a sphere consistently and its electron in the outside of the sphere. An ep is an epn of a hydrogen atom. Hydrogen atoms have also 4 kinds of ep spin models as showed in Figure 1 which seem to be useful on movement and for stability.

The discharge of hydrogen or helium is not the pure interference like coherent wave. Since hydrogen and helium are gases, they make line spectra through discharge in the quartz cylinder. To make the line spectra the mixing among the discharges of atoms may occur. The optical interference is composed of 1, or 2, or 3 kinds of epns (eps). It may not be possible in the present diffraction grating equipment that more epns than 3 gather and discharge. A characteristic of optical interference is that its intensity is obtained by productions (collisions), not by smooth vector additions. The optical interference of one kind of epn means that one proton, its neutron and its electron are composed to make a line spectrum in collision. In the optical interference of one epn, 3 points (one electron, its proton, its neutron) make one face. The points have different electricity one another as we see in Figure 2 which is showed in Ref. [4] . Each point attracts one another by consuming its mass as Einstein said. Finally they make one point face and then have the largest intensity. The optical interference of 2 epns means that 2 faces make 90˚ - 180˚. According to the proceedings of discharge of each epn, their intensities are obtained by the production of the intensities of two epns, and their combination angle decreases the intensity. The optical interference of 3 epns is described in the same manner.

Figure 1. Atomic epn spin models of hydrogen.

Figure 2. Three resonances (photons) in an interference of an epn.

2. Atomic Models and Line Spectra

In order to find the evidence which the atoms have 4 kinds of the orbital spins, we looked over the line spectra from hydrogen to the atoms which we can figure out. It is recorded that the gas, hydrogen (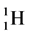) whose atomic spin models are shown in Figure 1 has 8 line spectra which are recorded in Ref. [5] . Even if it is hard to handle its original reference and its precise contents about the line spectra, we could guess some plausible physical concepts. We get the number from four solo epn optical interference line spectra of 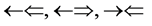and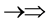, three two epns optical interference line spectra of 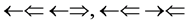and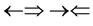, one three epns interference line spectrum of. 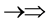Here X-ray spin () does make the two epn and three epn line spectra with the other spins, but they are not measured. In the above the double arrow means a proton and the single arrow its electron.

The basic epn spin alignments of 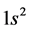of the gas, 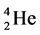whose atomic spin models are shown in Figure 3 are, , 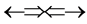and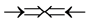. In the above the double arrow means a proton (+neutron) and the single arrow its electron. It is believed that the epns in the atom are seen to be perfect symmetric but not to be symmetric in making line spectra because each epn in the axes makes its own solo optical interference line spectrum. Here Pauli’s exclusion principle is applied. As we see in Figure 4 and Figure 5 the bonding and non-bonding between two orbital neutrons in the core of helium atom are the attraction between the different

Figure 3. Atomic epn spin models of helium.

Figure 4. Bondings between a proton and a neutron in a helium atom.

charges on the neutrons and the sliding by the same direction, basing on the stability of the atom. Hence for 33 line spectra of helium atom [5] we can get exactly the number 33 from 8 solo epn optical interference line spectra (, , , , , and). 15 two epns optical interference line spectra, 10 three epns optical interference line spectra. Here two X-ray epn spins (,) do also make two and three epns optical interference line spectra, but they are not recorded. In the above when 10 three epns make the optical interference line spectra, they should be counted in one way since the electricity discharges in the one side. It makes them, going forwardly, but not backwardly.

For 48 line spectra [5] of or its isotope whose atomic models are shown in Figure 6 we counted the combination number of epn spins as follows. Lithium is a solid and a metal. They are made by metal bonding to make clusters. We thought that the two proton (+neutron) and two electron spins of of lithium are, , , , , , and. The other proton spins (and) are not stable. We draw epns of with 4 energy levels of two kinds of protons (+neutron) by two kinds of electrons, considering the epn spin arrangements of in Table 1.

Figure 5. Nonbondings between a proton and a neutron in a helium atom.

Figure 6. Atomic epn spin models of lithium atoms.

Table 1. epn spin alignments of lithium cluster.

Total number of different epn spins of atoms in a cluster: 32. Total number of each epn spin 24, 24, 24, 24.

One cluster of lithium metal has 32 atoms of different epn spins [6] . Then the number of epn spins for each energy level is 24. Finally for 48 line spectra of one cluster lithium metal we can get the number exactly from 24 × 2 of which 2 means two energy levels () which excites firstly and secondly.

For 72 line spectra [5] of whose atomic spin models are shown in Figure 7 we can get the number of 72 exactly by counting the number of line spectra of one lowest excitation energy spin (or) from two X-ray spin alignments of of beryllium with the resonance of a free neutron, (a) (b) and the rest 7 spins, (c) (d) (e) (f) (g) (h) (I), and those of, (a’) (b’) (c’) (d’) (e’) (f’) (g’) (h’). If the spin of axis and the spin of axis meet with the lowest energy spin (or), its excitation occurs. So then the counting is possible.

For 25 line spectra of [5] whose atomic spin epn model is shown in Figure 8, we could get the number easily. The triangular three axes of and make the angular axes of 120˚. Each two symmetry axis of like helium may make the perpendicular axes to the triangular plane of and like lithium cluster. When these five axes epns make one cluster of the semi-metal of boron, 24 lowest energy epns (or) may be excited like one lithium cluster. Another one spectrum may belong to the excitation of or of.

The electronic configuration of whose atomic model is shown in Figure 9 is. Three axes of, and are perpendicular to one another. The basic spin alignments of its and axes becomes, , , , , , and

. Therefore for 61 line spectra [5] we can get 64 () line spectra for the whole excitation of

the lowest energy level epns spin (or) from one cluster of 256 epns (obtained by adding one axis (four kinds of epns) to lithium cluster). If three (or four) spectra of the cluster surrounding with X-ray spins are

Figure 7. An atomic epn spin resonance model of a free neutron in beryllium.

Figure 8. An atomic epn spin model of boron.

Figure 9. An atomic epn spin model of carbon.

abbreviated, we get 61 from 64. The existence of the molecule of may relates to this type of explanation. It is not reasonable to count the line spectra with, and axes since 8 unstable proton (+neutron) spin alignments of, , , , , , and by production of and appear. So Hund’s rule of the maximum multiplicity of the epn spins in a l level is not applied in this study as it is discussed more or less negatively [7] [8] .

The electronic configuration of atom is. With the ignorance of the basic epn spin alignments of and axis become, , and since it is non-metal like helium atom and the basic possible epn spin alignments of axis become and.

Hence for 74 line spectra [5] of nitrogen as a gas we get the number 76 from 20 solo epn optical inter- ference line spectra with the excitation of and of and and the excitation of of axis with 21 two epns optical interference line spectra and 35 three epns optical interference line spectra.

The electronic configuration of atom is It is a non-metal and hence each symmetric basic spin alignments of or or with ignorance of become, , and.

They all make 20 solo epn optical interference line spectra by taking as exciting of and. Among them one line spectra (or) of like boron and each two line spectra () of and take part in optical interference. Then for 40 line spectra [5] of we get 40 line spectra exactly from 20 solo epn optical interference line spectra, 10 two epns optical interference line spectra and 10 three epns optical interference line spectra.

For 24 line spectra [5] of whose atomic number is 15, epns cluster line spectra are counted same as those of lithium cluster. Then one level spins () are excited first.

3. Conclusions

The non-metal atoms like gases H, He, N, and O make one, two and three epns optical interference line spectra. Their, , , or axis spins which are, , and are believed to be perfectly symmetric. But if the out-most axis has one epn, it has four kinds of spin axis of, , and. This guess comes by counting the line spectra of H, He, N, etc. correctly.

1) The epns of metal atoms like Li, Be and Na do not make the interference line spectra. They make line spectra by forming the different spin alignments. The guess comes by counting the line spectra of and correctly.

2) Hund’s rule is not applied. The epns of all atoms here have a tendency to be paired first. A free neutron is situated in the cores of the atoms seen from the resonance of. epn of the atoms also may have a tendency to be paired to have stability.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Humphreys, C.J. and Kostkowski, H.J. (1952) Infrared Spectra of Noble Gases (12000 to 19000 A). Journal of Research of the National Bureau of Standards—Physics and Chemistry, 49, 73-84. http://dx.doi.org/10.6028/jres.049.010
[2]	Martin, W.C. (1960) Energy Levels and Spectrum of Neutral Helium (4HeI). Journal of Research of the National Bureau of Standards—Physics and Chemistry, 64, 19-28. http://dx.doi.org/10.6028/jres.064A.003
[3]	Litzen, U. (1970) Improved Experimental Values for Some Hydrogen-Like Levels of He I. Physica Scripta, 2, 103-105. http://dx.doi.org/10.1088/0031-8949/2/3/006
[4]	Kim, D., et al. (2010) New Physics: Sae Mulli (The Korean Physical Society), 60, 729-740.
[5]	Lide, D.R. and Frederikse, H.P.R. (1997) CRE Handbook of Chemistry and Physics. 78th Edition, CRE Press, 10-52.
[6]	Hecht, E. (2000) Optics. 2nd Edition, Korean Translators, Jangsu and Cho Jae-Heeng et al., 466.
[7]	Levine, I.N. (1978) Physical Chemistry. McGraw-Hill Co., 587.
[8]	Ishigaki, Y. and Yasuhara, H. (2002) Journal of the Korean Physical Society, 40, 1056-1059.