A Maximum Principle for Smooth Infinite Horizon Optimal Control Problems with State Constraints and with Terminal Constraints at Infinity ()
1. Introduction
The aim of this paper is, in a control problem with unilateral state constraints and terminal conditions at infinity, to obtain necessary conditions, with a full set of transversality conditions at infinity, which frequently make it possible to narrow down the set of candidates for optimality to only a few, or sometimes a single one. In infinite horizon problems without unilateral state constraints (pathwise constraints), with or without terminal conditions on the states at the infinite horizon, there exist various types of necessary conditions for optimality, and examples are [1] (without a transversality condition), and a number of results with certain limited types of transversality conditions, for example [2] , slightly generalized in [3] . See the latter paper and [4] for several further references (see also [5] ). The limited types of transversality conditions mentioned are in problems with several states-often insufficient if one wishes to avoid getting an infinite number of candidates. With strong growth conditions there exist necessary conditions, with a full set of transversality conditions at infinity, which in many cases make it possible to narrow down the set of candidates to only a few, or sometimes a single one, see Theorem 16, p. 2441 in [5] . For nonsmooth problems with a full set of transversality conditions in the infinite horizon case, see [6] . For such problems, see also [7] .
The novelty of the results in this paper is hence the establishment of necessary conditions that include a full set of transversality conditions at infinity in an infinite horizon problem with both terminal constraints at the infinite horizon and unilateral state constraints (constraints of the form 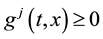 for all t). Strong growth conditions are needed for the results to hold.
for all t). Strong growth conditions are needed for the results to hold.
For Michel-type necessary condition in the case of unilateral state constraints, sees [8] .
The growth conditions used below, ((11), (12), (13)) are more demanding than the conditions applied in [9] for the case of no unilateral state constraints and no terminal constraints (problems with a dominant discount). In later work the authors use even more general conditions, see [10] (see also [11] , and [12] for problems with a special structure).
The results below are of especial interest in the case where not all states are completely constrained at infinity. In the opposite case, generalizations of Halkin’s infinite horizon theorem in [1] to problems with unilateral state constraints where no transversality conditions appear, like Theorem 9, p. 381 in [6] , frequently yield enough information for determining one or a few candidates for optimality. When not all states are completely constrained at infinity, transversality conditions related to the terminal conditions are needed, unless one can accept the possibility of an infinite number of candidates for optimality.
In certain cases there is a danger of degeneracy of multipliers. See the early review in [13] and [14] . We have added conditions that secure nondegeneracy of multipliers in some such cases, in particular in the case where unilateral constraints are satisfied as equalities by the initial state (the state at time zero). See [15] -[17] for a presentation of similar conditions in the finite horizon case, as well as for a number of references for this case (see for example [18] -[22] ).
2. The Control Problem, Necessary Conditions, and Examples
Consider the problem
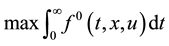 (1)
(1)
where 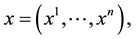 subject to
subject to
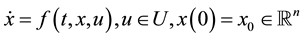 (2)
(2)
 (3)
(3)
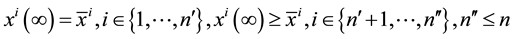 (4)
(4)
where we require that 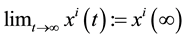 exists for
exists for  and where
and where 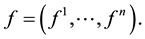 Here,
Here, 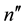
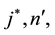 and n are given natural numbers, and we allow for the case where there are no equality constraints or no inequality constraints in (4) (in which cases
and n are given natural numbers, and we allow for the case where there are no equality constraints or no inequality constraints in (4) (in which cases 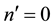 and
and 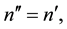 so
so  and/or
and/or 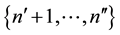 are empty sets). Furthermore,
are empty sets). Furthermore, 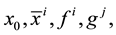
![]() are fixed entities, u the control. It is possible that
are fixed entities, u the control. It is possible that
![]() in which case
in which case ![]() is replaced by
is replaced by ![]() We want to maximize the objective in (1) over the set
We want to maximize the objective in (1) over the set
![]() of all measurable functions
of all measurable functions ![]() taking values in U and being bounded on bounded time intervals, subject
taking values in U and being bounded on bounded time intervals, subject
to (2)-(4). When the solution ![]() corresponding to such a
corresponding to such a ![]() satisfies (2)-(4), we call
satisfies (2)-(4), we call ![]() admissible. Below
admissible. Below ![]() will be a given optimal admissible pair, assumed to exist.
will be a given optimal admissible pair, assumed to exist.
We assume that ![]() is continuous in
is continuous in ![]() that
that ![]() is measurable in
is measurable in ![]() continuous in
continuous in ![]() with derivatives
with derivatives ![]() and
and![]() , where
, where ![]() is continuous in x and
is continuous in x and ![]() is continuous in
is continuous in
![]() We also assume, for any bounded sets
We also assume, for any bounded sets ![]() and
and ![]() that
that ![]()
and that for any x, ![]() These assumptions are called the basic smoothness
These assumptions are called the basic smoothness
assumptions. At various points some strengthening of these assumptions are added.
The following definitions are needed: let ![]()
![]()
![]()
![]() let
let ![]() be the resolvent of the equation
be the resolvent of the equation
![]() (
(![]() I the identity map),
I the identity map), ![]() if
if ![]()
![]()
![]()
![]()
![]()
In Theorem 1, in addition to the basic assumptions, assumptions (5)-(15) below are needed. It is assumed that for all ![]()
![]() (5)
(5)
We shall make use of some constraint qualifications, (6) and (8) below, related to ![]() Define
Define ![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() (6)
(6)
((6) holds vacuously if![]() ).
).
![]() (7)
(7)
![]() (8)
(8)
![]()
![]()
![]() (9)
(9)
Either2
![]()
![]()
![]()
![]() (10)
(10)
The following growth conditions are also needed: For some ![]()
![]() (11)
(11)
and there exist some positive constants ![]() such that
such that
![]() (12)
(12)
![]() (13)
(13)
where![]() . In (10) (g), we also need that for some
. In (10) (g), we also need that for some ![]()
![]() for all
for all ![]()
![]()
Assume finally that, for all j
![]() (14)
(14)
![]() (15)
(15)
Define ![]() The following necessary conditions for optimality holds.
The following necessary conditions for optimality holds.
Theorem 1. (Necessary condition, infinite horizon) Assume (5)-(8), (11)-(15) and the basic smoothness as
sumptions. There exist a number ![]() vectors
vectors![]() ,
, ![]() bounded vector functions
bounded vector functions ![]() and
and ![]()
![]() nondecreasing and right continuous on
nondecreasing and right continuous on![]() , such that if
, such that if ![]() 3 satisfies, for
3 satisfies, for![]() , the equation
, the equation
![]() (16)
(16)
then ![]() (the limit does exist),
(the limit does exist), ![]()
![]() is left continuous on
is left continuous on ![]() and satisfies (16) for
and satisfies (16) for ![]() (the integrals exist), and
(the integrals exist), and
![]() (17)
(17)
Moreover,
![]() (18)
(18)
![]() (19)
(19)
![]()
![]() (20)
(20)
Finally, ![]() for some
for some ![]() and if (6) fails, then (18) must be replaced by
and if (6) fails, then (18) must be replaced by ![]() ,
,
Remark 1. For ![]() the growth condition in (13) can be weakened to : For some
the growth condition in (13) can be weakened to : For some ![]() for all
for all ![]()
![]() (where still
(where still ![]() satisfies
satisfies![]() ). ,
). ,
In the sequel three trivial examples with rather obvious optimal controls will be presented, but to illustrate the use of the necessary conditions, we derive the form of the optimal controls from these conditions.
Example 1.![]()
![]() ,
, ![]()
![]() free,
free, ![]()
![]()
![]()
![]()
![]() free.
free.
Solution:
Evidently ![]() and, because
and, because ![]() by necessity,
by necessity, ![]() for all t. For
for all t. For ![]() from (16) we get
from (16) we get ![]()
![]() Then
Then ![]() The maxi- mum condition is that
The maxi- mum condition is that
![]() (21)
(21)
Consider first the case that we might have ![]()
![]()
![]() Let
Let ![]() satisfy
satisfy
![]() Now, for
Now, for ![]()
![]()
![]() means that
means that ![]() for t close to T,
for t close to T, ![]()
see the expression for ![]() so
so ![]() for t close to T. But this surely continues back to
for t close to T. But this surely continues back to ![]() (see
(see
the expression for ![]() again). So even
again). So even ![]() for
for ![]() (for such t, in fact,
(for such t, in fact, ![]()
when![]() ). Let
). Let ![]() be the smallest
be the smallest ![]() such that
such that ![]() for
for ![]() Consider first the subcase
Consider first the subcase ![]() Then
Then ![]() and by the expression for
and by the expression for![]() ,
, ![]() and
and ![]()
![]() By the maximum condition
By the maximum condition ![]() for
for ![]()
![]() for
for ![]() We must have
We must have ![]() in order to obtain
in order to obtain ![]() we get
we get
![]()
![]()
![]() for
for ![]()
![]() for
for ![]() so
so ![]() For
For ![]()
![]() (
(![]() an arbitrary constant). Using
an arbitrary constant). Using ![]() we get
we get ![]() hence
hence ![]() Thus,
Thus, ![]() ,
, ![]() with k satisfying
with k satisfying ![]() i.e.
i.e. ![]() so
so ![]() (By the way, note here that as
(By the way, note here that as ![]() satisfies the equation for
satisfies the equation for ![]() we would know that
we would know that ![]() for some constant C, but
for some constant C, but ![]() would not determine the constant. This shows the usefulness of the formula
would not determine the constant. This shows the usefulness of the formula![]() ) The subcase
) The subcase ![]() is impossible, then
is impossible, then ![]() and
and ![]() The case
The case ![]()
![]() is impossible, then
is impossible, then ![]() for t close to T, so
for t close to T, so ![]() for such t and then for all t (see the expression for
for such t and then for all t (see the expression for![]() ). In fact,
). In fact, ![]() when
when ![]() so
so ![]() for all t, implying
for all t, implying ![]() and
and ![]() a contradiction. Consider finally
a contradiction. Consider finally ![]() Then, by (18),
Then, by (18), ![]() so
so ![]() and then
and then ![]() for t close to T, so
for t close to T, so ![]() for such t, in fact for all t (see the expression for
for such t, in fact for all t (see the expression for![]() ), and
), and ![]() Hence,
Hence, ![]() for all t, which gives
for all t, which gives ![]() and
and ![]() contradicting
contradicting ![]() ,
,
Remark 2. (Further non-triviality properties)
a) Replace (6) by the assumption that either ![]() is empty, or (if not), for some
is empty, or (if not), for some ![]() some
some ![]() for any
for any ![]() there exists a
there exists a ![]() such that
such that ![]() for all
for all ![]() where
where ![]() is assumed to exist. Assume also that
is assumed to exist. Assume also that ![]() and
and ![]()
![]() are bounded4. Then
are bounded4. Then ![]()
b) Assume in addition that, for any ![]() either
either ![]() is empty, or (if not), there exists a
is empty, or (if not), there exists a ![]() such that
such that ![]() for all
for all ![]() and, in case
and, in case ![]() that for each u,
that for each u, ![]() is continuous, that
is continuous, that ![]()
![]() is left continuous at each
is left continuous at each ![]() and has a limit when
and has a limit when ![]() Then
Then ![]() ,
,
For finite horizon normality conditions, see [23] and [24] .
The main reason for including the next theorem is that it forms a basis for obtaining Theorem 1, but it has some interest of its own.
It contains necessary conditions for the case where (14) and/or (15) fail, in particular where ![]() also depends on
also depends on ![]()
![]() We then need three conditions, see (25)-(27) below, that automatically hold if (14) and (15) are satisfied.
We then need three conditions, see (25)-(27) below, that automatically hold if (14) and (15) are satisfied.
Theorem 2. In the situation of Theorem 1, with (5), (6), (8), (14), and (15) deleted, assume that the three conditions (25), (26), (27) below are satisfied. Then the following necessary conditions hold: for some ![]() for some vector
for some vector ![]() and some bounded nonnegative finitely additive set functions
and some bounded nonnegative finitely additive set functions ![]() vanishing on sets of Lebesgue measure zero, for a.e. s, for all
vanishing on sets of Lebesgue measure zero, for a.e. s, for all ![]()
![]() (22)
(22)
where ![]()
![]()
![]() (
(![]() and the integrals exist). Moreover,
and the integrals exist). Moreover, ![]()
![]() satisfying (20). Finally, defining
satisfying (20). Finally, defining ![]() we have
we have
![]() (23)
(23)
![]() (24)
(24)
If (7) and (8) hold, ![]() Moreover,
Moreover,
![]() if, for some
if, for some ![]() and some positive
and some positive ![]()
![]() when
when ![]() for all
for all ![]()
![]() Finally, if both the last condition and (7) and (8) hold, then
Finally, if both the last condition and (7) and (8) hold, then
![]() ,
,
As before when ![]()
![]() is replaced by
is replaced by ![]()
Assume, for some arbitrarily large ![]() that the conditions (25)-(27) hold
that the conditions (25)-(27) hold
![]() (25)
(25)
Let ![]() be a solution on
be a solution on ![]() of
of ![]() for
for ![]() given. For some positive second order term
given. For some positive second order term ![]() (i.e.
(i.e.![]() ), if
), if ![]() then, for all j, for all
then, for all j, for all ![]()
![]() (26)
(26)
Moreover, for any given number ![]() and any given positive second order term
and any given positive second order term ![]() a positive second order term
a positive second order term ![]() exists such that the following property holds. Let
exists such that the following property holds. Let ![]() be a solution on
be a solution on ![]() of
of
![]() for
for ![]() given,
given,![]() . Then, if
. Then, if ![]()
![]() (27)
(27)
As an example in which (25)-(27) hold, consider a case where ![]() (11) and (12) hold for
(11) and (12) hold for ![]() where f
where f
is concave in x, and where, for some positive ![]()
![]()
![]()
![]()
![]() is
is ![]() and convex,
and convex, ![]() and
and ![]()
![]() all j,
all j, ![]() (For
(For ![]() in a short
in a short
hand notation
![]()
where ![]() which means that, a.e.,
which means that, a.e., ![]() so
so ![]()
![]() If
If ![]() then
then ![]() and then
and then ![]()
Remark 3. For Theorem 2 to hold, we can weaken (7) and the basic assumptions on ![]() and
and ![]() as follows: the derivatives
as follows: the derivatives ![]() and
and ![]() exist at
exist at ![]() for all t and the three conditions on
for all t and the three conditions on ![]() below are satisfied: For all
below are satisfied: For all ![]()
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
Moreover in the growth conditions (12) and (13), roughly speaking, the inequalities need not hold for states x that cannot possibly occur, more precisely, the conditions can be modified as follows. Define for each t,
![]()
![]()
![]() the solution of (2) corresponding to
the solution of (2) corresponding to![]() . Then (12), (13) need only hold for some
. Then (12), (13) need only hold for some ![]() for
for ![]() such that
such that ![]() In (10)(g) we must add the assumptions that, for some
In (10)(g) we must add the assumptions that, for some ![]()
![]() is differentiable in
is differentiable in ![]() at
at ![]() uniformly in
uniformly in ![]() with a derivative at this point bounded uniformly in
with a derivative at this point bounded uniformly in ![]()
Finally, U can be replaced by a time dependent subset ![]() where
where ![]()
![]() ,
, ![]() continuous, we then require all control functions to satisfy
continuous, we then require all control functions to satisfy ![]() We assume
We assume ![]() and in case
and in case ![]() in (9), we require
in (9), we require ![]() Then the maximum conditions (17) and (22) hold only for
Then the maximum conditions (17) and (22) hold only for ![]() (The set U can even be replaced by
(The set U can even be replaced by ![]() with (17) and (22) holding for
with (17) and (22) holding for ![]() We must then still require
We must then still require ![]() and, in (9),
and, in (9), ![]() In the proof below, the perturbations
In the proof below, the perturbations ![]() of the optimal control have to belong to
of the optimal control have to belong to![]() . ,
. ,
Example 2.
![]()
![]()
![]() for all t,
for all t, ![]()
![]()
![]() free. It is convenient to replace
free. It is convenient to replace ![]() by
by ![]() (Then (25)-(27) will be satisfied). Choose
(Then (25)-(27) will be satisfied). Choose ![]() as the largest possible
as the largest possible ![]() such that
such that ![]() for
for ![]() If
If ![]() and even, for some
and even, for some ![]()
![]() for all t, then
for all t, then ![]()
![]() so
so ![]() by the maximum condition
by the maximum condition
![]() (31)
(31)
and![]() , contradicting the last inequality. Consider now the case where
, contradicting the last inequality. Consider now the case where ![]()
Let ![]() be the set of time points s for which (31) holds. Now,
be the set of time points s for which (31) holds. Now, ![]() implies the existence of some
implies the existence of some ![]() for which
for which ![]() 5, (
5, (![]() see the state equation). If
see the state equation). If ![]()
![]() can be chosen arbitrarily large, if
can be chosen arbitrarily large, if ![]()
![]() can be chosen arbitrarily close to
can be chosen arbitrarily close to![]() . Now,
. Now, ![]() so
so ![]() If
If ![]() then
then ![]() (use (31) for
(use (31) for![]() ), implying
), implying ![]() contradicting
contradicting ![]() Hence,
Hence, ![]() (Note that this
(Note that this
argument would not work if we had replaced ![]() by, say,
by, say,![]() ). For
). For ![]() by (31),
by (31),
![]() and because
and because ![]() is strictly decreasing on
is strictly decreasing on ![]() (
(![]() is con-
is con-
stant on![]() ), in fact
), in fact ![]() on
on ![]() in fact on all
in fact on all ![]() by (31). Hence, on
by (31). Hence, on ![]()
![]() so
so ![]() is finite and
is finite and ![]() and
and ![]() It is easily seen by a similar argument that on
It is easily seen by a similar argument that on
![]()
![]() : to see this, having
: to see this, having ![]() on an interval
on an interval![]() , assuming that
, assuming that ![]() is as large as
is as large as
possible, is impossible: Let ![]() and define
and define ![]() Now,
Now, ![]() leads to
leads to ![]()
![]() on
on ![]() which is impossible, and both for
which is impossible, and both for ![]() and
and ![]() and for
and for ![]() and
and ![]() certain time points in
certain time points in ![]() close to
close to ![]() (i.e. arbitrarily large if
(i.e. arbitrarily large if![]() ) exist at which
) exist at which ![]() but then
but then ![]() in
in ![]() by (31), as
by (31), as ![]() is strictly decreasing in
is strictly decreasing in![]() . But
. But ![]() in
in
![]() contradicts
contradicts ![]()
![]() in
in![]() . Hence, on
. Hence, on![]() ,
, ![]() by (31), so
by (31), so ![]() or
or ![]() on
on ![]() (
(![]() can be represented by an integrable function
can be represented by an integrable function ![]() here). If we put
here). If we put![]() , we have a valid proposal for the multipliers (It can be seen that
, we have a valid proposal for the multipliers (It can be seen that ![]() is even necessary, compare (89(ii)) on p. 333 in [6] ).
is even necessary, compare (89(ii)) on p. 333 in [6] ).
Example 3.
![]()
![]()
![]()
![]() ,
, ![]()
![]() free. It is convenient to replace
free. It is convenient to replace ![]() by
by ![]() The maximum condition is
The maximum condition is
![]() (32)
(32)
Again, assuming, for some ![]() that
that ![]() for all t, and (in the opposite case)
for all t, and (in the opposite case) ![]() both yield contradictions. So
both yield contradictions. So ![]() Now,
Now, ![]() in (32) is impossible, so
in (32) is impossible, so ![]() all the time. But, due to the constraint
all the time. But, due to the constraint ![]() then
then ![]() all the time (see the state equation). Let
all the time (see the state equation). Let ![]() The maximum condition (32) yields
The maximum condition (32) yields ![]()
![]() , for
, for ![]()
![]() Now,
Now,![]() . The general solution is
. The general solution is ![]() To have the initial condition and
To have the initial condition and ![]()
![]() satisfied we need
satisfied we need ![]()
![]() and hence
and hence ![]()
Remark 4. Assume in the problem (1)-(7), (11)-(15), that ![]() is convex and that there are given additional constraints in the problem of the form
is convex and that there are given additional constraints in the problem of the form ![]()
![]() (Perhaps
(Perhaps ![]() In this case, here and below, replace
In this case, here and below, replace ![]() by
by![]() .) Assume that
.) Assume that ![]() is optimal in this problem. We assume for
is optimal in this problem. We assume for ![]() that
that ![]() is continuous and depends only on
is continuous and depends only on ![]()
![]() , that
, that ![]() and
and ![]() exist, that
exist, that ![]()
![]() that
that
![]() is continuous in
is continuous in ![]() uniformly in t and that
uniformly in t and that
![]() is
is ![]() in
in ![]() and measurable in t. We assume, for some positive constants
and measurable in t. We assume, for some positive constants ![]() for all
for all
![]() that for
that for ![]()
![]() and
and ![]() for
for ![]() and
and ![]() for
for ![]() and, for
and, for ![]() that
that ![]() and
and ![]() for
for ![]() and
and ![]() for
for ![]()
![]() Define
Define ![]() {
{![]() : For all
: For all ![]() such that
such that ![]()
![]() }. Assume that
}. Assume that ![]() and that (8) holds, for
and that (8) holds, for ![]() for
for
![]() in (9). Write
in (9). Write ![]()
![]()
![]() Then, in addition to
Then, in addition to ![]()
![]() and
and ![]() satisfying (20), (23), and (24),
satisfying (20), (23), and (24), ![]() there exist bounded non-
there exist bounded non-
negative finitely additive set functions ![]()
![]() also vanishing on Lebesgue null sets, such that (22) holds
also vanishing on Lebesgue null sets, such that (22) holds
for![]() , summing now over
, summing now over ![]() Moreover, for
Moreover, for ![]() for all
for all ![]()
![]() (33)
(33)
![]() (34)
(34)
(![]() and the integrals exist). Furthermore, for
and the integrals exist). Furthermore, for ![]() we have
we have ![]() on
on ![]() and on
and on ![]() for all
for all ![]() Finally,
Finally, ![]() where
where ![]() (If (6) fails, then the last property must be replaced by
(If (6) fails, then the last property must be replaced by![]() ).
).
When for some vectors![]() ,
, ![]()
![]() the following properties hold: the maxi-
the following properties hold: the maxi-
mum condition (17) holds for![]() , together with
, together with
![]() (35)
(35)
for all ![]() where now
where now ![]()
![]() (36)
(36)
and where, for some nonnegative ![]()
![]()
![]() ,
, ![]() ,
, ![]() for
for ![]() and
and ![]() for
for ![]() if
if ![]() or if
or if ![]() for
for ![]() Moreover,
Moreover, ![]() and in (36), for
and in (36), for ![]()
![]() can be
can be
represented by a bounded nondecreasing right-continuous function ![]() and, finally,
and, finally,
![]() (If (6) fails, then this property must be replaced by
(If (6) fails, then this property must be replaced by![]() ).
).
When, in addition, for some ![]() some
some ![]()
![]() for all
for all ![]() the inequality
the inequality ![]() holds for all t, then
holds for all t, then ![]() for
for ![]() and, for
and, for ![]() in both (36) and (35),
in both (36) and (35), ![]() can be represented by a nonnegative function
can be represented by a nonnegative function ![]() in
in ![]() (replace
(replace ![]() by
by![]() ) and, moreover,
) and, moreover, ![]() (If (6) fails, then this property must be replaced by
(If (6) fails, then this property must be replaced by![]() ). Finally, in this case, for a.e. t, for all
). Finally, in this case, for a.e. t, for all ![]()
![]() ,
,
3. Proofs of the Results
Proof of Theorem 2. To simplify the notation, instead of the criterion (1), we can and shall assume that ![]() is the criterion to be maximized,
is the criterion to be maximized, ![]() that
that ![]() is free, hence is not required to be equal to
is free, hence is not required to be equal to ![]() The proof will be carried out under the assumptions of Theorem 2, allowing for the weakening of these assumptions in Remark 3.
The proof will be carried out under the assumptions of Theorem 2, allowing for the weakening of these assumptions in Remark 3.
Overview of the proof. A rough outline of the proof is as follows. We are going to make a number of strong (needleshaped) perturbations of ![]() This gives rise to first order variations of the optimal trajectory (the
This gives rise to first order variations of the optimal trajectory (the ![]() - functions below). We introduce a convex subset of these variations (
- functions below). We introduce a convex subset of these variations (![]() below) consisting of variations satisfying a first order version of the unilateral constraint. We then introduce the convex set of endpoints (at infinity) of these variations as is standard in traditional proofs of the maximum principle, and show that it has to be separated from the set of “better, first order admissible” points, the set {
below) consisting of variations satisfying a first order version of the unilateral constraint. We then introduce the convex set of endpoints (at infinity) of these variations as is standard in traditional proofs of the maximum principle, and show that it has to be separated from the set of “better, first order admissible” points, the set {![]() for
for ![]() if
if ![]() } (The endpoints we consider consist actually only of the first
} (The endpoints we consider consist actually only of the first ![]() components of the state). The separation argument (carried out in
components of the state). The separation argument (carried out in![]() ) consists of a standard use of the Brouwer fixed point theorem combined with the fact the endpoints are “good” first order approximations of the endpoints of the exact solutions following from the perturbations. We need the fact that these exact solutions satisfy the unilateral state constraint, and this is shown first. The separating functional (
) consists of a standard use of the Brouwer fixed point theorem combined with the fact the endpoints are “good” first order approximations of the endpoints of the exact solutions following from the perturbations. We need the fact that these exact solutions satisfy the unilateral state constraint, and this is shown first. The separating functional (![]() -vector) is denoted
-vector) is denoted![]() . Another separation argument, carried out in
. Another separation argument, carried out in ![]() -space’ gives the multipliers
-space’ gives the multipliers ![]() related to the unilateral state constraints.
related to the unilateral state constraints.
Detailed proof. To avoid certain problems connected with coinciding perturbation time points, the following construction is helpful (we then avoid coinciding perturbation time points). Let ![]() be a countable dense set in
be a countable dense set in
![]() and let
and let ![]() be the set of right Lebesgue points of
be the set of right Lebesgue points of ![]() and all
and all ![]()
![]() in
in
![]() Then choose some set
Then choose some set ![]() of full measure (i.e. meas
of full measure (i.e. meas![]() ),
),
such that for each ![]() a subset
a subset ![]() of
of ![]() exists with the property that if
exists with the property that if ![]() and
and ![]() then
then ![]() and with the property that for each
and with the property that for each ![]() each
each ![]() there exists a sequence
there exists a sequence ![]() such
such
that ![]() and
and ![]()
![]() For any given
For any given ![]()
![]() let
let ![]() be the collection of
be the collection of ![]() -tuples of the type
-tuples of the type
![]()
![]()
![]()
![]() and for all
and for all ![]() such that
such that ![]()
![]() belongs
belongs
to ![]() and
and ![]() belongs to
belongs to ![]() (This means that for any
(This means that for any ![]()
![]() if
if ![]() then
then ![]() which implies
which implies![]() ). The separate treatment of the case
). The separate treatment of the case ![]() where we can have several perturbations at the same time, is useful for obtaining nondegeneracy results (i.e. informative necessary conditions). Below
where we can have several perturbations at the same time, is useful for obtaining nondegeneracy results (i.e. informative necessary conditions). Below ![]() is varying
is varying ![]()
Let ![]() and for
and for ![]()
![]() define
define
![]() (37)
(37)
and
![]()
![]()
![]()
where a sum over an empty set is put equal to zero. For ![]()
![]()
Let ![]() and note that
and note that ![]() is convex6. Define
is convex6. Define ![]() to be the convex subset of
to be the convex subset of ![]() consisting of functions
consisting of functions ![]() that satisfy: For some
that satisfy: For some ![]()
![]()
![]() (38)
(38)
where ![]()
The linear variations ![]() are the ones that will appear in the necessary conditions that will be obtained (see (53), (54) below). These variations are jumping at each perturbation time points, so, near these points, they do not approximate (to the first order) the corresponding (continuous) exact solutions. Yet, we are able to show that the latter solutions satisfy the unilateral constraints when
are the ones that will appear in the necessary conditions that will be obtained (see (53), (54) below). These variations are jumping at each perturbation time points, so, near these points, they do not approximate (to the first order) the corresponding (continuous) exact solutions. Yet, we are able to show that the latter solutions satisfy the unilateral constraints when ![]() belongs to
belongs to![]() . To show this, the “better”, continuous, approximations
. To show this, the “better”, continuous, approximations ![]() are used.
are used.
3.1. Satisfaction of the Unilateral Constraints by Perturbed Solutions
Fix a pair ![]() such that
such that ![]() satisfies (38) for certain numbers
satisfies (38) for certain numbers ![]()
![]()
![]() . Let
. Let ![]() be some number for which (25), (26) and (27) hold. There exists a
be some number for which (25), (26) and (27) hold. There exists a ![]() so small that
so small that
![]() (39)
(39)
To see this, choose ![]() such that (39) is satisfied in this manner both for
such that (39) is satisfied in this manner both for ![]() and (by using (25)) for
and (by using (25)) for ![]() Then, for
Then, for ![]()
![]()
![]() satisfies
satisfies
![]() (40)
(40)
For some positive ![]() for
for ![]() for all
for all![]() , when
, when ![]() then
then ![]() and
and ![]() are disjoint for all
are disjoint for all ![]() and, moreover,
and, moreover, ![]() if
if ![]()
(![]() is closed). Let
is closed). Let ![]() be the set of points
be the set of points ![]() in
in ![]() for which
for which
![]() (41)
(41)
Now,
![]() (42)
(42)
by (40) because ![]() in
in ![]() Let
Let ![]() and define
and define ![]() inductively by the for
inductively by the for
mula ![]() (
(![]() ). Let
). Let ![]() and, for
and, for ![]() let
let
![]()
![]() (see (37) for
(see (37) for![]() ). Then, assuming right continuity at
). Then, assuming right continuity at![]() , (see (9)7), it is easily seen that
, (see (9)7), it is easily seen that
![]() (43)
(43)
is small when ![]() is small,
is small, ![]() uniformly in
uniformly in ![]() See the arguments connected with (74) below. For
See the arguments connected with (74) below. For
![]() let
let ![]() for
for ![]() let
let ![]() for
for ![]()
![]() (recall that these intervals are disjoint when the left ends differ and that
(recall that these intervals are disjoint when the left ends differ and that
![]() ), and
), and ![]() elsewhere. Let
elsewhere. Let ![]() be the corresponding solution. Define
be the corresponding solution. Define
![]()
Now, for ![]() small,
small, ![]() for
for ![]() hence by (43) and the Lebesgue point property of
hence by (43) and the Lebesgue point property of ![]() and
and ![]() at
at ![]()
![]() is of the second order in
is of the second order in ![]() uniformly in
uniformly in ![]() and
and ![]() Let
Let ![]() We want to prove that for some
We want to prove that for some ![]()
![]() (44)
(44)
Because ![]() is bounded by assumption (25), and
is bounded by assumption (25), and ![]() is of the second order,
is of the second order, ![]() is of the second order, uniformly in
is of the second order, uniformly in ![]() Moreover,
Moreover, ![]() is of the second order, uniformly in
is of the second order, uniformly in ![]() by the boundedness of
by the boundedness of ![]() Hence, by (41), for some positive
Hence, by (41), for some positive ![]() for
for ![]()
![]() (45)
(45)
Next, it is well-known that
![]() (46)
(46)
uniformly in ![]()
![]() (see Lemma D in Appendix). Moreover, by the differentiability assumption on
(see Lemma D in Appendix). Moreover, by the differentiability assumption on ![]() at
at ![]() ((28)), for some positive second order term
((28)), for some positive second order term![]() , we have
, we have
![]() (47)
(47)
for all ![]() (because
(because ![]() is of the first order in
is of the first order in![]() ). Hence, for some positive second order term
). Hence, for some positive second order term ![]() for
for ![]()
![]() (48)
(48)
both for all ![]() by boundedness of
by boundedness of ![]() on
on ![]() (combine (46) and (47)) and for all
(combine (46) and (47)) and for all ![]() (com-
(com-
bine (27) and (26)). Then, by (45), for some positive ![]()
![]() for
for ![]()
![]()
![]() Moreover,
Moreover,
for some positive ![]() for
for ![]() for all t, by (48),
for all t, by (48),
![]() and (by (25)),
and (by (25)), ![]() uniformly in
uniformly in ![]()
![]() so uniformly for
so uniformly for ![]()
![]()
![]()
![]() (49)
(49)
Hence, (44) has been shown, and in particular, (see (42))
![]() (50)
(50)
So far, we have only used the basic assumptions and the first of the three conditions on ![]() in Remark 3, namely (28). The other two properties, (30) and (29), will be used in what follows.
in Remark 3, namely (28). The other two properties, (30) and (29), will be used in what follows.
We want to show that ![]() when
when ![]()
![]()
![]() Now,
Now, ![]() implies
implies ![]() for
for ![]()
![]() close to
close to ![]() (recall
(recall![]() ). Thus, by (40),
). Thus, by (40), ![]() for
for ![]() and
and ![]()
![]() For
For ![]() small (
small (![]()
![]() ),
),![]() when
when ![]()
![]() (by continuity,
(by continuity, ![]()
![]() is small, when
is small, when ![]() is small). Note that if
is small). Note that if ![]() for some
for some![]() ,
, ![]() is a convex combination of
is a convex combination of ![]() and
and ![]() (the former one has weight
(the former one has weight![]() ). Hence, for any
). Hence, for any ![]()
![]() belongs to the segment between
belongs to the segment between ![]() and
and ![]() hence
hence ![]() for
for ![]()
![]()
![]()
So far, we have proved (44) for ![]() recall that if
recall that if ![]() then for
then for![]() ,
, ![]() (in particular this holds for
(in particular this holds for ![]() so for
so for ![]() (44) holds for all
(44) holds for all![]() ).
).
Finally, let us prove (44) for ![]()
![]() We can assume that
We can assume that ![]() is so small that
is so small that
![]() if
if ![]()
![]() So consider the case where
So consider the case where![]() ,
, ![]()
Then the right derivative ![]()
![]() First
First
consider the subcase where ![]() and
and ![]() (only one
(only one![]() ). By (39),
). By (39),
![]()
![]() Combining the two last weak inequalities we get
Combining the two last weak inequalities we get ![]() Then
Then ![]() so
so ![]() for
for ![]()
![]() for
for ![]() small (
small (![]()
![]() ).
).
Consider next the subcase where ![]() contains several pairs
contains several pairs ![]()
![]()
![]()
![]() ,
,
![]() Using (43), it is easily seen that
Using (43), it is easily seen that
![]() When
When ![]() and
and ![]() we have that
we have that ![]() Now,
Now, ![]() by (39), so
by (39), so ![]() Hence we again get
Hence we again get ![]() for
for ![]()
![]() for
for ![]() small (
small (![]()
![]() ).
).
Thus, when ![]() satisfies (38), then
satisfies (38), then
![]() (51)
(51)
3.2. Local Controllability at Infinity
Observation 1. Define ![]() and
and ![]() {
{![]() for
for ![]() for all
for all ![]() with
with ![]() if
if ![]() }. Note that by Lemma B in Appendix, for all
}. Note that by Lemma B in Appendix, for all ![]() and
and![]() ,
,
![]() and
and ![]() exist. Let
exist. Let ![]() be the convex set
be the convex set
![]() (for
(for ![]() see (38)). If
see (38)). If![]() , then for some positive
, then for some positive![]() , some
, some ![]()
![]()
![]() where each
where each ![]() equals
equals ![]()
![]()
![]()
![]()
![]() linearly independent. Let
linearly independent. Let ![]() Then
Then ![]()
![]() for some vector
for some vector ![]() In fact, for each
In fact, for each ![]() there is a unique
there is a unique ![]() such that
such that ![]()
![]() evidently depends linearly on z, note that
evidently depends linearly on z, note that ![]() extends linearly to all
extends linearly to all![]() . Let
. Let ![]() and let
and let ![]() consist of all
consist of all ![]()
![]()
![]() for
for
the moment we allow the pairs in ![]() to be doubly indexed, (and the time points not to be ordered). Then
to be doubly indexed, (and the time points not to be ordered). Then
![]() where
where ![]() (as we have double
(as we have double
indices on![]() , we have double indices on the components of
, we have double indices on the components of![]() ). Note that
). Note that ![]()
![]() Of course, we can re-index the pairs in
Of course, we can re-index the pairs in ![]() (and so also the entities
(and so also the entities![]() ) by using a
) by using a
single index, with the time points in the pairs in increasing order. Let ![]() be the number of pairs
be the number of pairs ![]() We use
We use ![]() also as the name of the vector of reindexed pairs, and
also as the name of the vector of reindexed pairs, and ![]() for the vector consisting of all entities
for the vector consisting of all entities ![]() reindexed in the same manner as the pairs in
reindexed in the same manner as the pairs in![]() . Then for
. Then for ![]()
![]()
![]()
![]() linear.
linear.
The following result should surprise nobody, a proof however is given in Appendix.
Lemma 1. Assume that for ![]()
![]()
![]() linear,
linear,![]()
![]() . Then there exist some first order term
. Then there exist some first order term ![]() (i.e.
(i.e.![]() ) and some
) and some ![]() such that for each
such that for each ![]() for some
for some ![]() some
some ![]()
![]() ,
, ![]()
![]() ,
,
3.3. Separation Arguments That Yield the Multipliers
By optimality, for all ![]()
![]() To see this, assume, by contradiction the opposite,
To see this, assume, by contradiction the opposite,
that for some ![]()
![]() Then by Observation 1 and Lemma 1, for
Then by Observation 1 and Lemma 1, for ![]() and small,
and small,
for some ![]()
![]()
![]() and
and ![]() satisfies the unilateral time constraint (3), see (51) (because
satisfies the unilateral time constraint (3), see (51) (because ![]() and
and![]() ). The last equality gives that
). The last equality gives that ![]() satisfies the terminal constraint (4) for
satisfies the terminal constraint (4) for ![]() small, and that
small, and that ![]() This contradicts the optimality of
This contradicts the optimality of![]() . Thus the sets
. Thus the sets ![]() and
and ![]() are disjoint (this is trivial if
are disjoint (this is trivial if![]() ). Thus these sets can be separated8: there exists a nonzero vector
). Thus these sets can be separated8: there exists a nonzero vector ![]() such that
such that ![]() As
As ![]() this inequality gives that
this inequality gives that
![]() (52)
(52)
Define ![]() {
{![]() : for all j, for some positive
: for all j, for some positive![]() ,
, ![]() ,
, ![]() when
when ![]() }. Recall that
}. Recall that ![]() for all
for all ![]() see (25), and write
see (25), and write![]() . Note that
. Note that ![]() (for
(for![]() , see (38)) has to be disjoint from the convex body
, see (38)) has to be disjoint from the convex body ![]() in
in ![]() otherwise the inequality
otherwise the inequality ![]() is contradicted. By separation, for some continuous linear functional
is contradicted. By separation, for some continuous linear functional ![]() on
on ![]() and some number
and some number ![]()
![]()
![]() (53)
(53)
for all ![]() all
all ![]() Evidently, by this inequality,
Evidently, by this inequality, ![]() and
and ![]() are nonnegative on
are nonnegative on![]() , with
, with ![]() for all
for all ![]() Each
Each ![]() can be represented by a bounded
can be represented by a bounded
finitely additive nonnegative set function ![]() vanishing on sets of Lebesgue measure zero. Evidently,
vanishing on sets of Lebesgue measure zero. Evidently, ![]() va-
va-
nishes on ![]() for all
for all ![]() in particular
in particular ![]() vanishes on
vanishes on ![]() The inequality (53) gives that, for
The inequality (53) gives that, for![]() ), for all pairs
), for all pairs ![]()
![]()
![]() (
(![]() still fixed in
still fixed in![]() ) and for all pairs
) and for all pairs ![]()
![]()
![]() and
and ![]()
![]() (54)
(54)
where ![]() (To obtain (54), in (53) let
(To obtain (54), in (53) let![]() ). Moreover, (54) also holds for
). Moreover, (54) also holds for![]() , for
, for ![]() for any given
for any given ![]()
Let us now choose a sequence ![]() converging to zero when
converging to zero when ![]() such that (54) holds in the manner
such that (54) holds in the manner
described for ![]() for certain multipliers
for certain multipliers ![]()
![]() In particular (54) holds for
In particular (54) holds for
![]() for any given
for any given ![]() Let us fix such a sequence
Let us fix such a sequence ![]() assuming it to be bounded. We can assume that
assuming it to be bounded. We can assume that ![]() (we extend
(we extend ![]() to
to ![]() by letting
by letting![]() ). Using the weak* topology on
). Using the weak* topology on ![]() there exists a cluster point
there exists a cluster point ![]() of the sequence
of the sequence ![]() satisfying
satisfying
![]() (55)
(55)
(for some subsequence ![]()
![]() ). (by the cluster point property, so the last
). (by the cluster point property, so the last
equality holds). The cluster point ![]() is a bounded nonnegative finitely additive set function that vanishes on Lebesgue null sets. It is furthermore easily seen that (54) holds for
is a bounded nonnegative finitely additive set function that vanishes on Lebesgue null sets. It is furthermore easily seen that (54) holds for ![]() and
and![]() , for
, for![]() ,
, ![]() and for
and for
![]() , both for
, both for ![]() equal to the cluster point
equal to the cluster point ![]() 9 as well as for
9 as well as for ![]() provided this limit exists, for any
provided this limit exists, for any ![]() for any given
for any given ![]()
![]()
Now ![]() is nondecreasing and bounded. Let
is nondecreasing and bounded. Let ![]() be the continuity points in
be the continuity points in ![]() of
of ![]()
![]() For any
For any ![]() and for any
and for any ![]() a sequence
a sequence ![]() exists, such that
exists, such that ![]() and
and ![]() (see the very beginning of this proof), and because (54) holds for
(see the very beginning of this proof), and because (54) holds for ![]() it is easily seen by taking limits that (54) holds for
it is easily seen by taking limits that (54) holds for ![]() and
and ![]() 10.
10.
Finally, let us extract an additional property. If ![]() for all t in some interval
for all t in some interval ![]() and
and ![]() then, for some
then, for some ![]()
![]() for
for ![]() when
when ![]() which by (55) implies
which by (55) implies ![]() and hence
and hence![]() . Thus
. Thus
![]() (56)
(56)
for (say) ![]() 11.
11.
3.4. Further Information on the Multipliers in Special Cases
Let us prove the results concerning the multipliers in the three last sentences in Theorem 2 in the case where ![]() is maximized.
is maximized.
Define
![]() (57)
(57)
Now, assume (9) and (10) (a), with ![]() We may assume of the sequence
We may assume of the sequence ![]() used above that
used above that ![]() for the single
for the single ![]() (there exists a sequence
(there exists a sequence ![]() such that
such that![]() ). Here (29) was used. Let
). Here (29) was used. Let ![]() satisfy the inequality in (9), define
satisfy the inequality in (9), define ![]() and assume that
and assume that ![]() Then, by (30), for some
Then, by (30), for some ![]() for
for ![]() close to 0,
close to 0, ![]() which combined with the previous inequality gives
which combined with the previous inequality gives ![]() So
So ![]()
![]() any given cluster point of
any given cluster point of![]() . We can assume that (54)
. We can assume that (54)
holds for this cluster point![]() , for
, for ![]()
Evidently, ![]() for all t close to 0. Now, if
for all t close to 0. Now, if ![]() and
and ![]() for all
for all ![]() then for any
then for any ![]()
![]() From
From ![]() we get, for all
we get, for all ![]() close to zero, that
close to zero, that ![]() which gives
which gives ![]() for
for ![]() close to zero, and so
close to zero, and so ![]() a contradiction. Hence,
a contradiction. Hence, ![]()
When ![]() and 0 is a right Lebesgue point of
and 0 is a right Lebesgue point of ![]() (i.e. (10) (b) holds), we can choose the sequence
(i.e. (10) (b) holds), we can choose the sequence ![]() Evidently, by (29),
Evidently, by (29), ![]() when
when ![]() so again
so again ![]()
![]() and we get the same conclusion regarding
and we get the same conclusion regarding ![]() (with
(with ![]() again) and in this case, (as well as in the case that
again) and in this case, (as well as in the case that ![]() is differentiable,
is differentiable,
i.e. (10) (g), see Appendix), we don’t need the assumption that ![]() contains a single element12. In fact,
contains a single element12. In fact,
when (8) holds, in Theorem 2, we can assume ![]()
Define ![]() Note that, by (23),
Note that, by (23), ![]() for
for ![]() large enough if
large enough if ![]() Assume that a
Assume that a ![]() and positive numbers
and positive numbers ![]() and
and ![]() exist such that
exist such that
![]() (58)
(58)
(see the end of Theorem 2). For ![]()
![]()
Assume for the moment that ![]() Choose a sequence
Choose a sequence ![]() such that
such that ![]() Letting
Letting ![]() in the preceding inequality, and using
in the preceding inequality, and using ![]() (see Appendix, Lemma A), we get
(see Appendix, Lemma A), we get ![]() so
so ![]()
Can![]() ? No, we have shown that then
? No, we have shown that then![]() , and then
, and then ![]() so
so ![]() a contradiction. So when (58) holds
a contradiction. So when (58) holds
![]() (59)
(59)
Finally, assume that both (58) and (8) are satisfied. By contradiction assume now that
![]() Then
Then ![]() (Þ
(Þ![]() and
and![]() , so
, so ![]() a contradiction. So (58) and (8) imply
a contradiction. So (58) and (8) imply
![]() (60)
(60)
Proof of Theorem 1.
We still keep the assumption that ![]() is maximized. Using lemmas in Appendix, note that (25)-(28) are implied by the basic smoothness assumptions, the growth conditions (11)-(13), (7), (14) (i.e.
is maximized. Using lemmas in Appendix, note that (25)-(28) are implied by the basic smoothness assumptions, the growth conditions (11)-(13), (7), (14) (i.e. ![]() depends only
depends only
on![]() ,
,![]() ), and (15) implying that
), and (15) implying that ![]() is differentiable at 0, uniformly in t ((27) follows from Lemma E in Appendix). Moreover, also (29), (30) evidently follow. So all the above results also hold in the situation of Theorem 1. Using the definition (57) the maximum condition (54) can be written
is differentiable at 0, uniformly in t ((27) follows from Lemma E in Appendix). Moreover, also (29), (30) evidently follow. So all the above results also hold in the situation of Theorem 1. Using the definition (57) the maximum condition (54) can be written
![]() (61)
(61)
Now, ![]() Using
Using ![]() (5) and (14),
(5) and (14), ![]() when
when ![]() Then, by (57), also
Then, by (57), also ![]() exists, and
exists, and ![]() Hence,
Hence, ![]() when
when ![]()
Let ![]() Let
Let ![]() be the continuity points of all
be the continuity points of all ![]() Write for the moment
Write for the moment
![]()
and ![]() Then13, for
Then13, for ![]()
![]() and then
and then ![]()
![]() With
With ![]() (
(![]() occurring in the definition of
occurring in the definition of![]() ) it is well-known that
) it is well-known that ![]() satisfies (16)14. Evidently, (61) yields
satisfies (16)14. Evidently, (61) yields
![]() (62)
(62)
In Theorem 1, we have written ![]() and
and ![]() instead of
instead of ![]() and
and![]() .
.
Note that (6) implies that (58) holds, as![]() ,
,![]() . Thus, (60) holds, which means that
. Thus, (60) holds, which means that
![]() in the situation of Theorem 1, because then
in the situation of Theorem 1, because then ![]() exists and equals
exists and equals![]() .
.
Proof of Remark 2. We give a proof for the case where ![]() is maximized. Note that
is maximized. Note that
![]() for
for ![]() for
for ![]() where
where ![]() is a set of Lebesgue points of
is a set of Lebesgue points of ![]() of full measure. The inequality holds for all
of full measure. The inequality holds for all ![]() in case of left continuity of
in case of left continuity of![]() .
.
Proof of a)
Let ![]()
![]() and recall
and recall ![]() Assume
Assume ![]() Assume by contradiction that
Assume by contradiction that ![]() Then, for all
Then, for all ![]() large enough
large enough
![]()
![]()
(the last term is ![]() all square brackets
all square brackets ![]() when
when![]() ). Then
). Then ![]() which is a contradiction because
which is a contradiction because ![]() for
for ![]() So
So ![]() cannot be
cannot be ![]() when
when![]() . Hence
. Hence ![]() implies
implies ![]()
Proof of b) Assume by contradiction that ![]()
If ![]() then for some arbitrary large
then for some arbitrary large ![]() we must have
we must have ![]() For
For ![]() for all j, for large
for all j, for large ![]() the left hand side is
the left hand side is ![]() i.e. it does not change much if
i.e. it does not change much if ![]() is replaced by
is replaced by![]() . Hence, for
. Hence, for ![]() (whether
(whether ![]() or =1), for large
or =1), for large![]() , for
, for ![]() as in a),
as in a),
![]()
Using the vectors ![]() in a), for
in a), for ![]() large we then have
large we then have ![]() Because
Because ![]() when
when ![]() s large, we finally get
s large, we finally get ![]() when
when ![]() is large. When s is large
is large. When s is large ![]() means
means ![]()
![]() Using
Using ![]() and (22) (which even holds for
and (22) (which even holds for ![]()
![]() ), for
), for ![]() large, we get
large, we get ![]() Hence, both for
Hence, both for ![]() and for
and for ![]()
![]() for some (large) s.
for some (large) s.
Next, let ![]() By contradiction, assume
By contradiction, assume ![]() Let
Let ![]() where
where ![]() has the property that
has the property that ![]() for
for ![]() see b). By continuity, for any
see b). By continuity, for any ![]() and close to
and close to ![]()
![]() (63)
(63)
There exist ![]()
![]() and arbitrarily close to
and arbitrarily close to ![]() such that for
such that for ![]()
![]() . If
. If ![]() for all j, the left hand side is
for all j, the left hand side is ![]() so for
so for ![]() close to
close to ![]()
![]() for all
for all ![]() whether
whether ![]() or
or ![]() Combining this inequality with (63), we get for
Combining this inequality with (63), we get for ![]() s close to
s close to ![]() that
that ![]() for
for ![]() 15. From this, we finally get, by Lipschitz continuity of
15. From this, we finally get, by Lipschitz continuity of ![]() on
on![]() , uniformly in s, that there exists a
, uniformly in s, that there exists a ![]()
![]() and close to
and close to ![]() such that
such that ![]() when
when ![]() and
and ![]() can be chosen so close to
can be chosen so close to ![]() that
that ![]() when
when ![]()
![]() The last inequality and (22) then yields
The last inequality and (22) then yields ![]() which gives
which gives ![]() both for
both for ![]() and for
and for ![]() and so
and so ![]() for all j. Evidently we cannot have
for all j. Evidently we cannot have ![]() so
so ![]() Thus
Thus ![]() contradicting
contradicting ![]() Hence
Hence ![]()
Proof of Remark 4. We construct an auxiliary problem: assume for given functions ![]() that we want to maximize
that we want to maximize ![]() subject to
subject to
![]() (64)
(64)
![]()
![]()
![]() measurable. Here
measurable. Here ![]()
![]() are auxiliary states, governed by
are auxiliary states, governed by ![]()
![]()
![]() where
where ![]() are auxiliary controls. Write
are auxiliary controls. Write ![]() For
For ![]() define
define ![]() {
{![]()
![]()
![]() if
if ![]()
![]() },
}, ![]() , and let
, and let ![]() Below,
Below, ![]() is so small that
is so small that ![]() Given any measurable control functions
Given any measurable control functions ![]()
![]()
![]() let
let ![]()
![]() be the solutions of (64) and
be the solutions of (64) and ![]() corresponding to
corresponding to ![]()
![]() . For any
. For any ![]() there exists a
there exists a ![]() such that if
such that if ![]() and
and ![]() then
then ![]() for all t, by Lemmas B and C in Appendix, hence, by continuity of
for all t, by Lemmas B and C in Appendix, hence, by continuity of ![]() at
at ![]() uniformly in t, for some
uniformly in t, for some ![]()
![]()
![]() for
for ![]() when
when ![]() and
and ![]() (
(![]() and
and ![]() perhaps dependent on
perhaps dependent on![]() ). In the auxiliary problem the constraints are the terminal constraints (4),
). In the auxiliary problem the constraints are the terminal constraints (4), ![]()
![]()
![]() for all
for all ![]() for
for ![]()
![]() for all
for all ![]() for
for ![]()
![]() Hence, if
Hence, if ![]() is admissible in the auxiliary problem, we have seen that
is admissible in the auxiliary problem, we have seen that ![]() is admissible in the original problem when
is admissible in the original problem when ![]()
![]() We assume that
We assume that ![]() is
is ![]() (for
(for ![]() see the beginning of Remark 4, then
see the beginning of Remark 4, then ![]() and then, for
and then, for ![]() the property related to
the property related to ![]() in Remark 3 is satisfied in the auxiliary problem for
in Remark 3 is satisfied in the auxiliary problem for![]() ). So, in the auxiliary problem,
). So, in the auxiliary problem, ![]()
![]() are optimal in the set of controls {
are optimal in the set of controls {![]()
![]()
![]()
![]() }. The arguments in the proof of Theorem 2 apply also in the present situation, with one modification: For
}. The arguments in the proof of Theorem 2 apply also in the present situation, with one modification: For ![]() the inequality
the inequality ![]() in
in ![]() for
for ![]()
![]() automatically holds for
automatically holds for ![]() Hence the arguments in the section between (50) and (51) are not needed16 (and do not work) for
Hence the arguments in the section between (50) and (51) are not needed16 (and do not work) for ![]()
The necessary conditions in Theorem 2 are now applied to this auxiliary system (they apply even when admissible controls are restricted as above, see the inequalities involving ![]() and even for
and even for ![]() replaced by
replaced by ![]() see the end of Remark 317. In the auxiliary system, the linearized system is
see the end of Remark 317. In the auxiliary system, the linearized system is ![]()
![]() where
where ![]() is the transposed of
is the transposed of ![]() The resolvent of the linearized system becomes
The resolvent of the linearized system becomes
![]() (65)
(65)
where ![]()
![]() From Lemma A in Appendix, we get that
From Lemma A in Appendix, we get that
![]() (66)
(66)
for some constant Q, independent of t and![]() , where
, where ![]() is the i’th row of B and
is the i’th row of B and ![]() (to apply Lemma A, note that for
(to apply Lemma A, note that for ![]()
![]() in an obvious notation,
in an obvious notation, ![]()
![]() where
where ![]()
![]()
![]()
![]() ). Note that (22), or actually (54), applied to the auxiliary system, holds for
). Note that (22), or actually (54), applied to the auxiliary system, holds for ![]() for the limit point
for the limit point ![]()
![]() given,
given, ![]() any given element in
any given element in ![]() (see remarks subsequent to (55)). From this we get, for
(see remarks subsequent to (55)). From this we get, for ![]() and
and ![]()
![]() and
and ![]() that
that
![]() (67)
(67)
From now on assume ![]() in (67). Moreover, for
in (67). Moreover, for ![]()
![]() from (54) applied to the auxiliary system, we get that (54) holds as written. Finally,
from (54) applied to the auxiliary system, we get that (54) holds as written. Finally, ![]()
![]() defined below.
defined below.
Let ![]() consist of all pairs
consist of all pairs ![]() such that
such that ![]() satisfies (52) and
satisfies (52) and ![]() satisfies
satisfies ![]()
![]() for all
for all ![]() and (56) for
and (56) for ![]() with
with ![]() Let
Let ![]()
![]()
![]() consist of all pairs
consist of all pairs ![]() such that (67) holds for the given
such that (67) holds for the given ![]() and (54) are satisfied for all
and (54) are satisfied for all ![]() for a.e. s, in particular for
for a.e. s, in particular for ![]()
![]() and
and ![]()
![]() any given
any given
cluster point of any given sequence![]() , each
, each ![]() corresponding to some collection
corresponding to some collection ![]() from
from![]() .
.
Let ![]() consist of all finite set
consist of all finite set ![]()
![]()
![]() We have just proved that for each
We have just proved that for each![]() ,
, ![]() is nonempty, so by compactness
is nonempty, so by compactness ![]() is nonempty (the weak* topology is applied on the m’s ). Let
is nonempty (the weak* topology is applied on the m’s ). Let ![]() be any given element in the latter intersection. Then, for
be any given element in the latter intersection. Then, for![]() , both
, both
(67) holds for all ![]() and (54) is satisfied for
and (54) is satisfied for ![]() for a.e. s. (To obtain this last property, preferably the set
for a.e. s. (To obtain this last property, preferably the set ![]() of point s for which (54) holds should be independent of the
of point s for which (54) holds should be independent of the![]() ’s in each
’s in each![]() , one can use that (54) now holds for
, one can use that (54) now holds for![]() , for
, for ![]() for
for![]() ,
, ![]() and hence by earlier limit arguments (54) holds for
and hence by earlier limit arguments (54) holds for![]() , for all
, for all![]() , for a.e. s). We also have that (54) is satisfied by
, for a.e. s). We also have that (54) is satisfied by ![]() for
for ![]() for any given cluster point
for any given cluster point ![]() for any given sequence
for any given sequence![]() , each
, each ![]() corresponding to some
corresponding to some
![]() for some
for some![]() .
.
The proof of ![]() is the same as the proof for the analogous condition in the case
is the same as the proof for the analogous condition in the case ![]() noting that
noting that ![]() for some
for some ![]() means for some
means for some ![]()
![]() for t near 0 (so
for t near 0 (so ![]()
![]() again leads to a contradiction in the same way as before)18. Similarly,
again leads to a contradiction in the same way as before)18. Similarly, ![]() has essentially the same proof as before. To show
has essentially the same proof as before. To show ![]() in case
in case ![]() holds, we now assume
holds, we now assume ![]() and we replace
and we replace ![]() by
by ![]() in the definition of
in the definition of ![]() where
where ![]()
![]() Then from (66), we get
Then from (66), we get
![]() (68)
(68)
Using the inequality
![]() (69)
(69)
(i.e. (67)), we get
![]() (70)
(70)
Note that ![]() So, from (68), (70) and
So, from (68), (70) and![]() ,
, ![]() it follows that
it follows that ![]() Then
Then
![]()
![]() (note the
(note the ![]() -norm on
-norm on![]() ). But then
). But then![]() ,
, ![]() can be
can be
represented by nonnegative functions ![]() in
in ![]() in fact in
in fact in ![]() because
because ![]() is bounded.
is bounded.
Let us finally show that ![]() when
when ![]() exists. By (66), for
exists. By (66), for ![]()
![]()
![]() independent of
independent of ![]() and
and ![]()
![]() So, for
So, for ![]()
![]() ,
, ![]() By this inequality, there exists a
By this inequality, there exists a ![]() such that, for
such that, for ![]()
![]() for
for ![]()
![]() Next, for some
Next, for some![]() , for
, for ![]()
![]()
![]()
![]() for
for![]() . To see this, for k chosen such that
. To see this, for k chosen such that ![]()
![]() for
for ![]() note that
note that ![]() when
when ![]() By (67) and the two inequalities involving
By (67) and the two inequalities involving ![]() for
for![]() , and for
, and for ![]() for any
for any ![]()
![]()
But then ![]()
![]() because
because ![]() was arbitrary. A contradiction of
was arbitrary. A contradiction of ![]() has arisen, so
has arisen, so ![]()
4. Conclusion
The paper establishes necessary conditions for optimality in a smooth infinite horizon optimal control problem with unilateral state constraints and terminal constraints at the infinite horizon. The necessary conditions include a complete set of transversality conditions at infinity. The specific growth conditions placed upon the system in this paper can easily be modified, but strong growth conditions are in any case needed for the full set of necessary conditions to hold.
Acknowledgements
I was deeply grateful to the referees. Their detailed comments made it possible to correct omissions and improve the exposition.
Appendix
Below, for any matrix ![]()
![]() .
.
Lemma A. Let ![]()
![]()
![]() let
let
![]()
where, in![]() , the matrices in the first row are respectively
, the matrices in the first row are respectively ![]() and
and ![]() and in the second row
and in the second row ![]() and
and![]() , and, in
, and, in![]() ,
, ![]() is
is ![]() and
and ![]() is
is ![]() all entries being measurable functions of
all entries being measurable functions of ![]()
![]() and
and ![]() locally integrable. Assume that for some positive numbers
locally integrable. Assume that for some positive numbers ![]()
![]()
![]()
![]()
![]()
![]() Write
Write ![]() for the solution
for the solution ![]() on
on![]() ,
, ![]() , of
, of ![]() for
for ![]() given. Define
given. Define ![]() Then for some positive number Q, only dependent on
Then for some positive number Q, only dependent on
![]()
![]()
![]() Hence
Hence ![]()
Lemma B. Let ![]() and
and ![]() be measurable in t, and with
be measurable in t, and with![]() ,
, ![]()
![]() and
and ![]() Lipschitz continuous with Lipschitz constants
Lipschitz continuous with Lipschitz constants![]() ,
, ![]() ,
, ![]() and
and![]() , respectively,
, respectively, ![]() Write
Write ![]()
![]() There exists a positive number
There exists a positive number ![]() such that the following properties hold: let
such that the following properties hold: let
![]() and
and ![]() be two solution on
be two solution on ![]() of
of ![]() for
for![]() , respectively
, respectively ![]() given, assumed to exist. Then for all t,
given, assumed to exist. Then for all t, ![]() and
and![]() , so
, so ![]() which implies that
which implies that ![]() exists if
exists if ![]() exists. ,
exists. ,
Note that ![]() and
and ![]() do exist whenever
do exist whenever ![]() and
and ![]() are integrable.
are integrable.
The proofs of the lemmas A and B are of a standard type and omitted in order to save space.
Let ![]() be given and let
be given and let ![]() Let
Let ![]()
Lemma C. Let ![]() be a family of functions
be a family of functions ![]() such that all
such that all ![]() are Lipschitz
are Lipschitz
continuous in ![]() with a common Lipschitz rank
with a common Lipschitz rank ![]()
![]() integrable, and with
integrable, and with ![]() measurable. Let
measurable. Let
![]() be a solution of
be a solution of ![]()
![]() and
and ![]() given (assumed to exist). Assume that all
given (assumed to exist). Assume that all
![]()
![]() are bounded by a common constant
are bounded by a common constant![]() . Then a constant
. Then a constant ![]() exists such
exists such
that for any ![]() for any given
for any given![]() , a solution of
, a solution of ![]()
![]() exists, and
exists, and
![]() for all
for all![]() .
.
Proof of Lemma C. Note that ![]() so by Gronwall’s inequality,
so by Gronwall’s inequality, ![]()
Lemma D. Let ![]() be a family of functions
be a family of functions ![]() all Lipschitz continuous in x with a
all Lipschitz continuous in x with a
common Lipschitz rank![]() ,
, ![]() integrable, and with
integrable, and with ![]() measurable. Let
measurable. Let ![]() be a given function in
be a given function in ![]() and let
and let ![]() be a solution of
be a solution of![]() ,
, ![]() given (assumed to exist). We assume that all
given (assumed to exist). We assume that all
![]()
![]() are bounded by a common constant
are bounded by a common constant![]() . We also assume that
. We also assume that ![]() is differentiable at
is differentiable at ![]() for a.e. t. For
for a.e. t. For ![]() let
let ![]() be a solution of
be a solution of ![]()
![]()
![]() given. Then, for some
given. Then, for some ![]() for all t,
for all t, ![]() when
when ![]()
![]() Moreover, for some
Moreover, for some ![]() and some second order term
and some second order term ![]() for all t, all
for all t, all ![]() all
all ![]() all f such that
all f such that ![]()
![]() where
where ![]() is the solution of
is the solution of ![]()
![]() given (it does exist).
given (it does exist).
Proof of Lemma D. The proof of ![]() follows from Lemma C. Let
follows from Lemma C. Let ![]() and let
and let ![]() on
on ![]()
![]() We have that
We have that ![]() and, by differentiability of
and, by differentiability of ![]() at
at ![]() we have that
we have that ![]() for some second order increasing term
for some second order increasing term![]() , so for
, so for
![]()
![]()
for a.e. t. Dividing by d, we get
![]()
By Lebesgue’s dominated convergence theorem, ![]() when
when![]() . As
. As
![]()
then
![]()
and then by Gronwall’s inequality,
![]()
where ![]() a second order term in d, equals
a second order term in d, equals ![]()
Lemma E. In the situation of Lemma B, let ![]() be differentiable at
be differentiable at ![]() where
where ![]() is a given solution on
is a given solution on ![]() of
of ![]()
![]() given, assumed to exist. For each
given, assumed to exist. For each ![]() let
let ![]() be a solution on
be a solution on ![]()
![]() of
of ![]()
![]() given (it does exist), and let
given (it does exist), and let ![]() be a solution of
be a solution of ![]()
![]() given. Assume that, for some K,
given. Assume that, for some K, ![]() for all
for all ![]()
![]() a second order term in d. Then for some second order term
a second order term in d. Then for some second order term![]() ,
, ![]()
Proof of Lemma E. By Lemma D, for some term ![]() being of the second order in d,
being of the second order in d, ![]() when
when ![]() is of the second order. For some
is of the second order. For some ![]()
![]() for
for ![]() Hence, by Lemma B, for some constants
Hence, by Lemma B, for some constants ![]()
![]() we have that
we have that ![]()
![]()
![]()
![]() so
so
![]()
By Lebesgue’s dominated convergence theorem the conclusion in the lemma follows if we can prove that for
each t, ![]() when
when ![]() To obtain the latter fact, let
To obtain the latter fact, let
![]() and note that
and note that
![]()
where the second order term ![]()
Proof of Lemma 1.
Consider the map ![]() for
for ![]() d any number in
d any number in![]() . Let
. Let ![]() and note that, by Lemma C,
and note that, by Lemma C, ![]() and
and ![]() are continuous in
are continuous in ![]() Then, by Lemma B,
Then, by Lemma B, ![]() and
and ![]() are continuous in
are continuous in ![]() Let
Let ![]() be a Lipschitz rank of
be a Lipschitz rank of ![]() and
and![]() . For
. For ![]() let the second order term
let the second order term ![]() satisfy
satisfy
![]() when
when ![]()
![]()
for the existence of ![]() see Lemmas D and E. Recall that
see Lemmas D and E. Recall that ![]() and that
and that ![]() when
when ![]() for some second order term
for some second order term![]() , see an argument preceding (44) and Lemma A. Hence, for
, see an argument preceding (44) and Lemma A. Hence, for![]() ,
,
![]() when
when ![]()
![]()
Note that for ![]() we have
we have ![]() as
as![]() , and for d small (
, and for d small (![]() for some
for some![]() ),
), ![]() Fix such a
Fix such a![]() . Now,
. Now, ![]() is continuous in
is continuous in ![]() and has a fixed point
and has a fixed point ![]() here, by Brouwer’s fixed point theorem. As
here, by Brouwer’s fixed point theorem. As ![]() and
and ![]()
![]()
![]()
![]() Then let
Then let ![]()
![]() to obtain Lemma 1.
to obtain Lemma 1.
Observation A. On the space of continuous real-valued functions on ![]() with compact support, furnished with the sup-norm,
with compact support, furnished with the sup-norm, ![]() can be represented by a nondecreasing bounded function
can be represented by a nondecreasing bounded function ![]() such that
such that ![]() for all bounded continuous
for all bounded continuous ![]() with compact support. In fact, we can let
with compact support. In fact, we can let ![]()
![]() , (
, (![]() right continuous for
right continuous for![]() ). Let
). Let ![]() be the continuity points in
be the continuity points in ![]() of
of ![]() Then
Then ![]() for any
for any ![]() hence for
hence for ![]()
![]() and
and ![]() so
so ![]() is also left continuous at s. For piecewise constant functions
is also left continuous at s. For piecewise constant functions ![]() with bounded support, jumping only at points in
with bounded support, jumping only at points in ![]() evidently
evidently ![]() By approximating continuous function (or even piecewise continuous functions jumping only at points in
By approximating continuous function (or even piecewise continuous functions jumping only at points in![]() ) by such piecewise constant functions, one see that the same equality holds for continuous functions (or such piecewise continuous functions)
) by such piecewise constant functions, one see that the same equality holds for continuous functions (or such piecewise continuous functions) ![]() with bounded support.
with bounded support.
Note that if ![]() uniformly (
uniformly (![]() continuous, with a common bounded support), and
continuous, with a common bounded support), and ![]() then
then![]() : Assuming for simplicity (say)
: Assuming for simplicity (say)![]() , this follows from
, this follows from
![]()
Let ![]()
![]() arbitrary. For
arbitrary. For ![]()
![]() large,
large, ![]() hence, for any
hence, for any ![]()
![]() Thus for
Thus for ![]()
![]()
![]() Hence,
Hence, ![]() when
when ![]() If
If ![]() is bounded and continuous, but with unbounded support, evidently, by the last inequality,
is bounded and continuous, but with unbounded support, evidently, by the last inequality, ![]() so
so ![]() exists. As also
exists. As also ![]() (
(![]()
![]() ), exactly the same argument works for
), exactly the same argument works for ![]() the latter limit written
the latter limit written ![]()
Proof of (10) (g) Þ ![]()
Assume again that ![]() is maximized and postulate the conditions in Theorem 2 (allow even for the conditions in Remark 3), in particular postulate (10) (g). For simplicity, assume
is maximized and postulate the conditions in Theorem 2 (allow even for the conditions in Remark 3), in particular postulate (10) (g). For simplicity, assume ![]() for
for ![]()
![]() for
for ![]()
![]() We want to replace each condition
We want to replace each condition ![]()
![]() by two conditions,
by two conditions, ![]() for
for ![]()
![]() for
for ![]() It can be done by requiring that
It can be done by requiring that ![]()
![]() holds for
holds for ![]() and, by adding new constraints
and, by adding new constraints ![]() required to hold on
required to hold on![]() , where
, where ![]() for
for![]() . We now first assume both that
. We now first assume both that![]() ,
, ![]() is independent of t, and that
is independent of t, and that ![]() is independent of t for
is independent of t for![]() . Assume that there exist
. Assume that there exist![]() ,
, ![]()
![]()
![]() (see (9)) such that
(see (9)) such that
![]() (71)
(71)
Then, for some ![]() both
both
![]() (72)
(72)
and, for ![]()
![]() (73)
(73)
Let ![]() have the property that
have the property that ![]() and
and ![]() for
for ![]() Let
Let
![]() be a first order term (i.e.
be a first order term (i.e. ![]() when
when![]() ), such that
), such that
![]() when
when ![]() for all
for all![]() , i. As we did in connection with (43), let
, i. As we did in connection with (43), let ![]() and define inductively
and define inductively ![]()
![]() . Let
. Let![]() . Choose a partition
. Choose a partition ![]()
![]() of
of ![]() such that
such that![]() . Define
. Define ![]() It is easily seen that for
It is easily seen that for ![]()
![]() (74)
(74)
for any ![]() To see this, note that for
To see this, note that for ![]() the left hand side vanishes, while for
the left hand side vanishes, while for ![]()
![]() the left hand side is smaller that
the left hand side is smaller that ![]() Let
Let ![]() Define
Define ![]()
![]()
![]() Let
Let ![]() be any given number,
be any given number, ![]()
![]() such that
such that ![]() and
and ![]() when
when![]() .
.
Let ![]()
![]() Moreover, let
Moreover, let ![]()
![]() Then
Then ![]() when
when ![]()
![]() as
as![]() . So
. So ![]() when
when ![]()
Consider the following auxiliary control problem on![]() . Define
. Define ![]()
![]() Let
Let ![]() and introduce the two state equations
and introduce the two state equations ![]()
![]()
![]() ,
, ![]()
![]() free, and let
free, and let ![]() and
and ![]() be the controls. We require
be the controls. We require ![]() on
on ![]() for
for ![]() and
and
![]() on
on ![]() for
for ![]() and
and ![]()
![]() described below. The end conditions on
described below. The end conditions on ![]() are as before. Then
are as before. Then ![]() and
and ![]() (on
(on![]() ) are optimal in this problem, see below. Applying Theorem 2 to this problem, with
) are optimal in this problem, see below. Applying Theorem 2 to this problem, with ![]() and
and ![]() as costates corresponding to
as costates corresponding to ![]() and
and![]() , gives
, gives ![]()
![]()
![]() for all
for all ![]()
![]() for
for ![]()
![]()
![]() and the maximum condition (22), i.e. (a.e.)
and the maximum condition (22), i.e. (a.e.)
![]()
![]()
![]()
![]() ,
,
where
![]()
![]() ,
,
![]() In particular, because
In particular, because ![]() when
when ![]()
![]() see (72), then
see (72), then
![]() (75)
(75)
Assume by contradiction both that ![]() and that
and that ![]() where
where ![]() which by necessity means that
which by necessity means that ![]() Then, fo r
Then, fo r
![]()
![]() ,
,
![]() for
for ![]()
![]() for
for ![]()
![]() for
for ![]() which gives
which gives ![]() and
and ![]() for
for ![]() and
and ![]() for
for![]() . Also,
. Also, ![]() by (73). As
by (73). As![]() , using (74), we have, for
, using (74), we have, for![]() ,
,
![]()
contradicting ![]() for
for ![]() (as
(as ![]() is optimal).
is optimal).
The optimality of ![]() follows from the following argument: Let
follows from the following argument: Let ![]() be an arbitrary admissible quadruple in the auxiliary problem. Let
be an arbitrary admissible quadruple in the auxiliary problem. Let ![]() If
If ![]() let
let ![]()
![]()
![]() for
for ![]() let
let ![]()
![]() for
for ![]() and let
and let![]() ,
, ![]() for
for ![]() Next, let
Next, let ![]()
![]()
![]() Then
Then
![]()
and hence ![]() Moreover,
Moreover, ![]()
So ![]()
![]() is a solution in the original system evidently satisfying the end restrictions, and
is a solution in the original system evidently satisfying the end restrictions, and ![]() for
for ![]()
![]() Because
Because ![]()
![]() for
for ![]()
![]()
![]() and then
and then ![]() for
for ![]()
![]() Finally, on
Finally, on ![]()
![]()
![]() as we shall see in a moment, so
as we shall see in a moment, so ![]() for
for ![]() hence
hence ![]() for all
for all ![]()
![]() For
For ![]() let
let ![]() in which case
in which case ![]() is automatically an original solution.
is automatically an original solution.
From (74) and ![]() for
for ![]() we get
we get
![]() (76)
(76)
Using ![]() when
when ![]() for
for ![]()
![]()
Then, by (72), (73), (76), for all ![]() all
all ![]() all
all ![]()
![]()
![]()
19In case we have constraints![]() ,
, ![]() , (in which case
, (in which case![]() ,
, ![]() is required), then for
is required), then for ![]() and
and ![]() small, for
small, for![]() ,
, ![]() , as
, as![]() .
.
As ![]() then
then ![]() for
for ![]()
![]() Moreover, for
Moreover, for ![]() for some positive
for some positive ![]() small enough,
small enough, ![]() when
when ![]()
![]() (For
(For ![]() there is nothing to prove.)
there is nothing to prove.)
Now, ![]() for
for ![]() so
so ![]() belongs to the set of admissible pairs in the original problem. We have
belongs to the set of admissible pairs in the original problem. We have ![]() hence
hence ![]()
![]() are optimal in the auxiliary problem19.
are optimal in the auxiliary problem19.
Let now ![]()
![]() where
where ![]() and let
and let ![]() and
and ![]() be corresponding multipliers, satisfying the normalization
be corresponding multipliers, satisfying the normalization ![]() We put
We put ![]() Now,
Now, ![]() has a cluster point
has a cluster point ![]() satisfying (22), (55), and (56). Assume now that
satisfying (22), (55), and (56). Assume now that ![]() . Then there exist some
. Then there exist some ![]() such that
such that ![]()
![]() and hence
and hence ![]() Hence,
Hence, ![]() which leads to a contradiction, as was shown above. Thus,
which leads to a contradiction, as was shown above. Thus,![]() .
.
We can extend this result to problems that are nonautonomous on![]() , by using t as a new state variable, say z, governed by
, by using t as a new state variable, say z, governed by ![]() with x governed by
with x governed by ![]() provided that
provided that ![]() is jointly differentiable in
is jointly differentiable in ![]() at
at ![]() for all t, and that
for all t, and that ![]() is differentiable in
is differentiable in ![]() at
at ![]() uniformly in
uniformly in ![]() with a derivative at this point bounded uniformly in
with a derivative at this point bounded uniformly in ![]()
NOTES
1In that theorem, correct the inequality ![]() by replacing it by
by replacing it by![]() .
.
![]()
2A right Lebesgue point s of any integrable function ![]() means a point s such that
means a point s such that![]() . If
. If ![]() in (9) even belongs to
in (9) even belongs to ![]() and (10) (b) holds, then the right continuity in (9) can be weakened to 0 being a right Lebesgue point of
and (10) (b) holds, then the right continuity in (9) can be weakened to 0 being a right Lebesgue point of ![]() for all
for all![]() .
.
![]()
3![]() always exists, and is left continuous on
always exists, and is left continuous on ![]() .
.
![]()
4For ![]() it suffices that
it suffices that ![]() when
when![]() ,
, ![]() , note that for
, note that for![]() ,
, ![]() for some C.
for some C.
![]()
5Or even![]() , an observation needed in the next example.
, an observation needed in the next example.
![]()
6One may consult Observation 1 below at this point.
![]()
7Only when there are more than one perturbation ![]() at
at ![]() right continuity is needed to obtain (43). If there is a single perturbation at
right continuity is needed to obtain (43). If there is a single perturbation at![]() , (i.e. for all
, (i.e. for all![]() ,
, ![]() = some
= some![]() ) it suffices that
) it suffices that ![]() is a right Lebesgue point of
is a right Lebesgue point of![]() . Finally, if
. Finally, if![]() , then we shall throughout assume a single perturbation
, then we shall throughout assume a single perturbation ![]() at
at![]() .
.
![]()
8If ![]() and
and![]() , then K and
, then K and ![]() can be separated. If
can be separated. If![]() , then for some nonzero
, then for some nonzero![]() ,
, ![]() , and
, and ![]() can be chosen such that
can be chosen such that![]() .
.
![]()
9For simplicity, assume that![]() . Then, for any
. Then, for any![]() , for all n large enough,
, for all n large enough, ![]() for all for
for all for![]() , so, by (25); for
, so, by (25); for![]() ,
, ![]() , for any
, for any![]() ; for all n large enough,
; for all n large enough, ![]() for all
for all![]() . As
. As![]() ,
, ![]() , so
, so![]() , which converges to zero at least for a subsequence of
, which converges to zero at least for a subsequence of![]() .
.
![]()
10If U is replaced by ![]() as in Remark 3, we asume that
as in Remark 3, we asume that![]() . The perturbations
. The perturbations ![]() will belong to
will belong to![]() , because in the proof we now require the
, because in the proof we now require the![]() ’s to belong to
’s to belong to ![]() and then
and then ![]() for t in
for t in![]() , for d small. Then (54) holds for a.e. s for
, for d small. Then (54) holds for a.e. s for ![]() (Þ
(Þ![]() for n) and also for
for n) and also for![]() , for any given cluster point
, for any given cluster point ![]() of any given bounded sequence
of any given bounded sequence ![]() where
where![]() ,
, ![]() ,
, ![]() In addition, (54) holds for
In addition, (54) holds for ![]() for all limits
for all limits ![]() of all such sequences
of all such sequences ![]() that are convergent. In particular, (54) holds for a given cluster point
that are convergent. In particular, (54) holds for a given cluster point ![]() of a given sequence
of a given sequence![]() , where
, where![]() ,
, ![]() given points in
given points in![]() ,
,![]() .
.
11In case![]() , it can be assumed that
, it can be assumed that![]() , for all j, and, as said before, we then assume that for all P,
, for all j, and, as said before, we then assume that for all P, ![]() ,
, ![]() some arbitrarily given element in
some arbitrarily given element in ![]() (in
(in ![]() in case U is replaced by
in case U is replaced by![]() ,
, ![]() for n large).
for n large).
![]()
12If (8) holds only for a subset ![]() of
of ![]() then it is easily seen that the collection
then it is easily seen that the collection![]() ,
, ![]() ,
, ![]() ,
, ![]() is nonzero (at least one entity is nonzero).
is nonzero (at least one entity is nonzero).
![]()
13Observation A in Appendix may be consulted at this point.
14Compare e.g. Section 9.5 in [16] .
![]()
15As an alternative to the left continuity assumption on ![]() in Remark 2 (for
in Remark 2 (for![]() ), we may assume that, if
), we may assume that, if ![]() in the necessary conditions, then these conditions imply left continuity of
in the necessary conditions, then these conditions imply left continuity of ![]() on
on![]() .
.
![]()
16Thus we don’t need (and often don’t have!) differentiability of ![]() for
for![]() .
.
17The growth conditions related to ![]() are of the same type as those related to
are of the same type as those related to ![]() in problem (1)-(4). Note that the perturbations
in problem (1)-(4). Note that the perturbations ![]() now belong to
now belong to![]() .
.
![]()
18We can again let![]() ,
, ![]() also in the present case, (67) does not change for this change of
also in the present case, (67) does not change for this change of![]() .
.