1. Introduction
In this paper, we address some issues related to the asymptotic behavior a hybrid system with two types of vibrations of different nature. The model under consideration is inspired in and introduced in [1] . However, there are some important differences between these two models. In [1] the flexible part of the boundary  is occu- pied by a flexible damped beam instead of a flexible. Most of the relevant properties see [2] . In [3] the authors are interested on the existence of periodic solutions of this system. Due to the localization of the damping term in a relatively small part of the boundary and to the effect of the hybrid structure of the system, the existence of periodic solutions holds for a restricted class of non homogeneous terms. Some resonance-type phenomena are also exhibited. Cindea, Sorin and Pazoto [4] consider the motion of a stretched string coupled with a rigid body at one end and we study the existence of periodic solution when a periodic force facts on the body. The main difficulty of the study is related to the weak dissipation that characterizes this hybrid system, which does not ensure a uniform decay rate of the energy. For more examples of hybrid systems see [5] [6] . We refer to [7] for a discussion on the model and references therein. In [8] the authors to discern exact controllability properties of two coupled wave equations, one of which holds on the interior of a bounded open domain
is occu- pied by a flexible damped beam instead of a flexible. Most of the relevant properties see [2] . In [3] the authors are interested on the existence of periodic solutions of this system. Due to the localization of the damping term in a relatively small part of the boundary and to the effect of the hybrid structure of the system, the existence of periodic solutions holds for a restricted class of non homogeneous terms. Some resonance-type phenomena are also exhibited. Cindea, Sorin and Pazoto [4] consider the motion of a stretched string coupled with a rigid body at one end and we study the existence of periodic solution when a periodic force facts on the body. The main difficulty of the study is related to the weak dissipation that characterizes this hybrid system, which does not ensure a uniform decay rate of the energy. For more examples of hybrid systems see [5] [6] . We refer to [7] for a discussion on the model and references therein. In [8] the authors to discern exact controllability properties of two coupled wave equations, one of which holds on the interior of a bounded open domain , and the other on a segment
, and the other on a segment 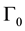 of the boundary
of the boundary . Moreover, the coupling is accomplished through terms on the boundary. Because of the particular physical application involved the attenuation of acoustic waves within a chamber by means of active controllers on the chamber walls control is to be implemented on the boundary only.
. Moreover, the coupling is accomplished through terms on the boundary. Because of the particular physical application involved the attenuation of acoustic waves within a chamber by means of active controllers on the chamber walls control is to be implemented on the boundary only.
We consider the bi-dimensional cavity 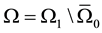 and that
and that  an open class C2 with limited boundary contained in Ω1, filled with an elastic, in viscid, compressible fluid, in which the acoustic vibrations are coupled with the mechanical vibration of a string located in the subset
an open class C2 with limited boundary contained in Ω1, filled with an elastic, in viscid, compressible fluid, in which the acoustic vibrations are coupled with the mechanical vibration of a string located in the subset  a part of the boundary of omega of
a part of the boundary of omega of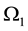 ,
,  and
and 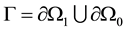 with
with  is boundary of
is boundary of . The subset
. The subset 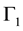 is assumed to be rigid and we impose zero normal velocity of the fluids on it. The subset
is assumed to be rigid and we impose zero normal velocity of the fluids on it. The subset 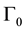 is supposed to be flexible and occupied by a flexible string that vibrates under the pressure of the fluid on the plane where
is supposed to be flexible and occupied by a flexible string that vibrates under the pressure of the fluid on the plane where  lies. The displacement of
lies. The displacement of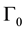 , described by the scalar function
, described by the scalar function![]() , obeys the one-dimensional dissipa- tive wave equation. As
, obeys the one-dimensional dissipa- tive wave equation. As ![]() is compressible fluid where the velocity field
is compressible fluid where the velocity field ![]() is given by the potential
is given by the potential ![]() All deformations are supposed to be small enough so that linear theory applies.
All deformations are supposed to be small enough so that linear theory applies.
The linear motion of this system is described by means of the coupled wave equations
![]() (1)
(1)
where ![]() denote the unit outward normal to
denote the unit outward normal to![]() .
.
We define the energy associated with this system. Proceeding formally, multiply the first equation by ![]() and then integrate over
and then integrate over![]() .
.
![]() (2)
(2)
However, the integral
![]()
which leads us
![]() (3)
(3)
Replacing (3) into (2) we obtain
![]() (4)
(4)
Multiplying by w in the second equation of the system (1) and then integrate over ![]()
![]() (5)
(5)
Integrating by parts
![]()
Replacing the above equation over (5) we obtain
![]() (6)
(6)
which leads us to assert that, the energy of the system is given by
![]() (7)
(7)
for each![]() .
.
Remark 1 The first two terms represents the energy of acoustic wave and the other terms is the energy of bungee wave.
The system has a natural dissipation. Indeed, to observe this fact multiply the first equation of (1) by ![]() and then the second equation of (1) by
and then the second equation of (1) by![]() , as was done in previous calculations
, as was done in previous calculations
![]() (8)
(8)
if ![]() Micu, S. in his doctoral thesis [7] shows non-exponential decay of the energy of the hybrid system (1).
Micu, S. in his doctoral thesis [7] shows non-exponential decay of the energy of the hybrid system (1).
2. Mathematical Formulation
Define the face space ![]() endowed with the Hilbertian scalar product given by
endowed with the Hilbertian scalar product given by
![]() (9)
(9)
for all ![]() We can show that the pair
We can show that the pair ![]() is a Hilbert space.
is a Hilbert space.
Since the first and second equation of the system (1), we obtain
![]()
![]()
These equations lead us to define the operator ![]() by
by
![]()
in this sense for all ![]()
![]() (10)
(10)
Note that ![]() if and only if
if and only if
![]()
Now, we consider the problem with Neumann boundary conditions
![]() (11)
(11)
where we can say that ![]() see [9] . Similarly, consider the problem
see [9] . Similarly, consider the problem
![]() (12)
(12)
We can say that ![]() In this sense we can define the domain of the operator
In this sense we can define the domain of the operator ![]() which we denote
which we denote![]() , as the set of
, as the set of ![]() such that
such that ![]()
![]()
![]()
![]() satisfying
satisfying
![]()
![]()
![]()
![]()
Remark 2 By previous observations we can say that the hybrid system (1) is equivalent to the Cauchy problem
![]() (13)
(13)
where ![]() and
and ![]()
3. Solution Existence
We want to show that ![]() is a dissipative operator and
is a dissipative operator and ![]() (The resolvent set of
(The resolvent set of![]() ).
).
Remark 3 The operator ![]() is dissipative, ie
is dissipative, ie ![]() for all
for all ![]()
Applying (9), we get
![]()
Resolvent Equation:
Given![]() , we find
, we find ![]()
![]() (14)
(14)
In particular, ![]() if and only if, there is
if and only if, there is
![]()
that is,
![]()
![]()
![]()
![]()
where ![]() By previous observations that there have
By previous observations that there have ![]() Using the application of Lummer Phillips Theorem [10] [11] , we have the following result.
Using the application of Lummer Phillips Theorem [10] [11] , we have the following result.
Theorem 1 The operator ![]() set to (10) is the infinitesimal generator of a contraction semigroup
set to (10) is the infinitesimal generator of a contraction semigroup ![]()
Theorem 2 The ![]() is the infinitesimal generator of a semigroup
is the infinitesimal generator of a semigroup ![]() and verifies
and verifies ![]() then the solution of (13) satisfies
then the solution of (13) satisfies
![]() (15)
(15)
4. Asymptotic Behavior
We now show that the energy associated with the system decays exponentially. Multiplying by ![]() the first equation in (1) and integrating over
the first equation in (1) and integrating over ![]() yields
yields
![]()
equivalently
![]() (16)
(16)
Observe that
![]() (17)
(17)
From the second equation in (1), we obtain
![]() (18)
(18)
On the other hand,
![]() (19)
(19)
From (17)-(19), we obtain
![]() (20)
(20)
Replacing (20) into (16)
![]() (21)
(21)
or equivalently
![]() (22)
(22)
Now, since Poincaré inequality we have
![]() (23)
(23)
where ![]() is the Poincaré constant. In a similar way,
is the Poincaré constant. In a similar way,
![]() (24)
(24)
From (22), (23) and (24) we have
![]() (25)
(25)
We define the operator
![]() (26)
(26)
Differentiating (26) and using (8) we obtain
![]() (27)
(27)
Considering n large enough, we can obtain a constant C such that
![]() (28)
(28)
On the other hand, using Poincaré, we can obtain
![]() (29)
(29)
In a similar way
![]() (30)
(30)
Moreover, from trace
![]() (31)
(31)
Replacing (31) into (30) we have
![]() (32)
(32)
From (23), (29), (32) and (26) we can to claim that there is a constant ![]() and
and ![]() such that
such that
![]() (33)
(33)
leading to decay exponentially energy
![]() (34)
(34)
where![]() . The result follows.
. The result follows.
Remark 4 In the case of ![]() can be also said that a power decays exponentially.
can be also said that a power decays exponentially.
The above results support the conclusion.
Theorem 3 If ![]() and
and ![]() then the solution
then the solution ![]() of the hybrid system (1) decays exponentially over time.
of the hybrid system (1) decays exponentially over time.
Acknowledgements
Octavio Vera thanks the support of the Fondecyt project 1121120.