Integrated and Explicit Boundary Conditions of Electromagnetic Fields at Arbitrary Interfaces between Two Anisotropic Media ()
1. Introduction
The boundary conditions are often expressed in two equations?continuity of the tangential components and discontinuity of the normal components of electromagnetic field intensities 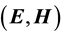 [1] . The former is yielded by applying Stokes’ law to a differential line integral on the interface between two media, and the latter is obtained by applying Gauss’ law to a differential sized cylinder surface containing a section of the interface. This gives two separate and implicit formulae that define “boundary equations” linking the boundary values of the fields in two anisotropic media. Two boundary equations are implicit functions of the interface normal
[1] . The former is yielded by applying Stokes’ law to a differential line integral on the interface between two media, and the latter is obtained by applying Gauss’ law to a differential sized cylinder surface containing a section of the interface. This gives two separate and implicit formulae that define “boundary equations” linking the boundary values of the fields in two anisotropic media. Two boundary equations are implicit functions of the interface normal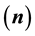 , electric conductivity and permittivity tensors
, electric conductivity and permittivity tensors , or magnetic permeability tensor
, or magnetic permeability tensor . In isotropic cases, it is not difficult to obtain the explicit formulae of the boundary values because all these tensors reduce to scalars that make the explicit solution straightforward. The difficulty is increased in applying the separate and implicit formulae to anisotropic media and arbitrary interface topography as they do not explicitly give the solutions of the boundary values, so that they must be individually or successively employed in electromagnetic field modeling. In addition, most of numerical modeling techniques, such as finite-difference, finite-element and boundary element methods approximate the boundary values with some numerical schemes, e.g. the finite-difference method often replaces the interfaces with great gradients to produce the “strong solution” of electromagnetic fields [2] . The finite-element method employs combinations of the edge-vectors to approach the field intensities so that the boundary conditions are satisfied at the sampled points [3] . However, the accuracy of the edge-vector approximation depends on the number of the samples of the edge-vectors [4] . Also, these numerical approaches cannot simultaneously produce the complete set of boundary values due to only involving one-side boundary values in the assembled linear equations, and need an explicit formula to recover another side boundary values. In order to simplify the implementation of the boundary conditions or recover whole boundary values at an interface, it is desirable to combine the two separate and implicit equations into a single integrated and explicit formula so that it can be more directly and easily applied to theoretical and numerical electromagnetic anisotropy problems.
. In isotropic cases, it is not difficult to obtain the explicit formulae of the boundary values because all these tensors reduce to scalars that make the explicit solution straightforward. The difficulty is increased in applying the separate and implicit formulae to anisotropic media and arbitrary interface topography as they do not explicitly give the solutions of the boundary values, so that they must be individually or successively employed in electromagnetic field modeling. In addition, most of numerical modeling techniques, such as finite-difference, finite-element and boundary element methods approximate the boundary values with some numerical schemes, e.g. the finite-difference method often replaces the interfaces with great gradients to produce the “strong solution” of electromagnetic fields [2] . The finite-element method employs combinations of the edge-vectors to approach the field intensities so that the boundary conditions are satisfied at the sampled points [3] . However, the accuracy of the edge-vector approximation depends on the number of the samples of the edge-vectors [4] . Also, these numerical approaches cannot simultaneously produce the complete set of boundary values due to only involving one-side boundary values in the assembled linear equations, and need an explicit formula to recover another side boundary values. In order to simplify the implementation of the boundary conditions or recover whole boundary values at an interface, it is desirable to combine the two separate and implicit equations into a single integrated and explicit formula so that it can be more directly and easily applied to theoretical and numerical electromagnetic anisotropy problems.
This paper derives two new integrated and explicit versions of the boundary conditions, called the explicit “normal” and “tangential” versions respectively. They successfully combine two common implicit boundary equations into a single explicit linear matrix formula without altering their applicability to interfaces that have arbitrary topography and two anisotropic media. These new versions consistently present the boundary values of electromagnetic field intensities  linked by a 3 × 3 matrix, which can be calculated with the known interface topography
linked by a 3 × 3 matrix, which can be calculated with the known interface topography  and tensors of model electric permittivity
and tensors of model electric permittivity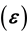 , conductivity
, conductivity  and magnetic permeability
and magnetic permeability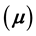 . We analytically demonstrate equivalence of the single matrix formula to two common implicit boundary equations, and show theoretical applications of the new versions to transformation of the boundary values from one-side to another in the boundary integral equation and boundary element approach. In addition, two synthetic experiments of utilizing the new versions are conducted, and show the advantage of the new versions of being a simpler and more straightforward method to recover the whole boundary values at arbitrary interfaces.
. We analytically demonstrate equivalence of the single matrix formula to two common implicit boundary equations, and show theoretical applications of the new versions to transformation of the boundary values from one-side to another in the boundary integral equation and boundary element approach. In addition, two synthetic experiments of utilizing the new versions are conducted, and show the advantage of the new versions of being a simpler and more straightforward method to recover the whole boundary values at arbitrary interfaces.
2. Boundary Conditions
In the frequency-domain, electric and magnetic field intensities  in anisotropic media satisfy Maxwell’s equations [5]
in anisotropic media satisfy Maxwell’s equations [5]
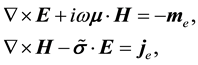 (1)
(1)
where 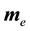 and
and 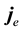 represent the external magnetic and electric current sources supplied by human or natural existence, and
represent the external magnetic and electric current sources supplied by human or natural existence, and 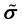 is the complex-valued tensor defined by:
is the complex-valued tensor defined by:
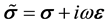 (2)
(2)
Here, 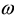 represents an angular frequency and
represents an angular frequency and ![]() are three tensors of magnetic permeability, electric conductivity and permittivity. The complex-valued conductivity tensor
are three tensors of magnetic permeability, electric conductivity and permittivity. The complex-valued conductivity tensor ![]() implies that the electric current density
implies that the electric current density ![]() consists of the conduction
consists of the conduction ![]() and displacement
and displacement ![]() current densities. In this paper,
current densities. In this paper, ![]() or
or ![]() are simply called the model property tensors because they define the electromagnetic properties of media. In isotropic cases, the model property tensors
are simply called the model property tensors because they define the electromagnetic properties of media. In isotropic cases, the model property tensors ![]() or
or ![]() are scalars, i.e.
are scalars, i.e. ![]() or
or![]() . In general, the field intensities
. In general, the field intensities![]() , model property tensors
, model property tensors ![]() or scalars
or scalars![]() , and external current sources
, and external current sources ![]() are functions of the spatial coordinates
are functions of the spatial coordinates![]() .
.
Applying Equation (1) and its zero-divergences ![]() and
and ![]() to a closed differential line integral and surface integral of a differential sized cylinder surface that contains a section of the interface between two media, respectively [1] , the following boundary conditions of the electric and magnetic field intensities are obtained:
to a closed differential line integral and surface integral of a differential sized cylinder surface that contains a section of the interface between two media, respectively [1] , the following boundary conditions of the electric and magnetic field intensities are obtained:
![]() (3)
(3)
![]() (4)
(4)
Here, the scalar quantities ![]() and
and ![]() are the normal components of the net external current densities at the interface:
are the normal components of the net external current densities at the interface:
![]() (5)
(5)
The superscripts “−” and “+” stand for the boundary values on the two sides of the interface, and ![]() is a unit normal of the interface (see Figure 1).
is a unit normal of the interface (see Figure 1).
In order to remove computational singularities (infinite value) of the external point sources ![]() and
and![]() , the field intensities are often expressed in two portions [2] [3] [6] , i.e.
, the field intensities are often expressed in two portions [2] [3] [6] , i.e.![]() , where
, where ![]() are the primary fields generated by
are the primary fields generated by ![]() and
and ![]() in a reference model given by
in a reference model given by![]() , and
, and ![]() are the secondary fields governed by the following equations obtained by substitution of the field decomposition into Equation (1):
are the secondary fields governed by the following equations obtained by substitution of the field decomposition into Equation (1):
![]() (6)
(6)
These equations demonstrate that the source terms of the secondary fields are ![]() and
and ![]() instead of
instead of ![]() and
and![]() , where
, where![]() , Similarly, Applying Equation (6) and its zero diver-
, Similarly, Applying Equation (6) and its zero diver-
gences to an interface of two media, and appointing![]() ,
, ![]() or
or![]() ,
, ![]() in the cases of
in the cases of ![]() or
or ![]() respectively, the following boundary conditions of the secondary fields are obtained:
respectively, the following boundary conditions of the secondary fields are obtained:
![]() (7)
(7)
![]() (8)
(8)
Here, ![]() and
and![]() . Equations (7) and (8) are also yielded by substituting
. Equations (7) and (8) are also yielded by substituting ![]() and
and ![]() into Equations (3) and (4) respectively, and then applying the same boundary conditions to the primary fields. Equations (3) and (4) or Equations (7) and (8) are general and applicable to any interface between two media. Here, we named these boundary conditions as the “implicit boundary equations” because they consist of two separate and implicit equations that involve the boundary values of the field intensities
into Equations (3) and (4) respectively, and then applying the same boundary conditions to the primary fields. Equations (3) and (4) or Equations (7) and (8) are general and applicable to any interface between two media. Here, we named these boundary conditions as the “implicit boundary equations” because they consist of two separate and implicit equations that involve the boundary values of the field intensities![]() , unit normal
, unit normal ![]() of an interface and model property tensors
of an interface and model property tensors![]() . By comparing Equation (3) with (4), or Equation (7) with (8), the similarities of the boundary conditions of magnetic fields to electric fields are observed. It is shown that the boundary conditions of magnetic fields can be obtained by simply replacing the electric field symbols
. By comparing Equation (3) with (4), or Equation (7) with (8), the similarities of the boundary conditions of magnetic fields to electric fields are observed. It is shown that the boundary conditions of magnetic fields can be obtained by simply replacing the electric field symbols ![]() with the magnetic field symbols
with the magnetic field symbols![]() . Therefore, derivations below will only deal with electric field whose result can be easily extended to magnetic field by the symbol replacements.
. Therefore, derivations below will only deal with electric field whose result can be easily extended to magnetic field by the symbol replacements.
3. Explicit Normal Version
Equation (3) can be rewritten in the following matrix form
![]() , (9)
, (9)
where the vectors ![]() and
and ![]() are defined by
are defined by ![]() and
and ![]() respectively, and the matrices
respectively, and the matrices ![]() are given by:
are given by:
![]() (10)
(10)
Here, the summation convention over the double subscripts ![]() has been applied, and the redundant row arising from curl calculation has been removed in three cases. Accordingly, the determinant of the matrix cannot be zero
has been applied, and the redundant row arising from curl calculation has been removed in three cases. Accordingly, the determinant of the matrix cannot be zero![]() , therefore, the matrix
, therefore, the matrix ![]() is invertible and its inverse matrix can be calculated by linear algebra:
is invertible and its inverse matrix can be calculated by linear algebra:
![]() (11)
(11)
where
![]() . (12)
. (12)
Multiplying ![]() to Equation (9) gives
to Equation (9) gives
![]() (13)
(13)
where
![]() , (14a)
, (14a)
or
![]() (14b)
(14b)
Here, ![]() is the Kronecker delta symbol. The above equation shows that the three cases given in Equations (10) and (11) are unnecessary in the matrix
is the Kronecker delta symbol. The above equation shows that the three cases given in Equations (10) and (11) are unnecessary in the matrix![]() . In this paper, the matrix
. In this paper, the matrix ![]() is called the boundary matrix because it is a function of the boundary conductivity tensors
is called the boundary matrix because it is a function of the boundary conductivity tensors ![]() and the unit normal
and the unit normal ![]() of the interface, and links the two boundary values of the field intensities. With the known interface normal
of the interface, and links the two boundary values of the field intensities. With the known interface normal ![]() and conductivity tensors
and conductivity tensors![]() , Equation (13) directly give the solution of the boundary values and successfully combines two implicit boundary equations into a single explicit linear matrix formula. This integrated and explicit form of the boundary conditions is advantageous to application without altering its applicability to any interface between two media. Therefore, Equation (13) is termed the “explicit normal versions” of the boundary conditions.
, Equation (13) directly give the solution of the boundary values and successfully combines two implicit boundary equations into a single explicit linear matrix formula. This integrated and explicit form of the boundary conditions is advantageous to application without altering its applicability to any interface between two media. Therefore, Equation (13) is termed the “explicit normal versions” of the boundary conditions.
Substituting ![]() into Equation (13) and then applying the same boundary conditions to the primary fields
into Equation (13) and then applying the same boundary conditions to the primary fields ![]() in the reference conductivity model:
in the reference conductivity model:![]() ,
, ![]() or
or![]() ,
, ![]() , the integrated and explicit boundary conditions of the secondary electric fields are obtained:
, the integrated and explicit boundary conditions of the secondary electric fields are obtained:
![]() (15)
(15)
This equation corresponds to Equation (7) but explicitly gives the boundary values of the secondary fields. It achieves transformation of the boundary values at an interface.
The explicit boundary conditions for magnetic fields can be obtained by replacing the electric symbols ![]() with the magnetic symbols
with the magnetic symbols ![]() in Equations (13) and (15), i.e.
in Equations (13) and (15), i.e.
![]() (16)
(16)
![]() (17)
(17)
From these explicit normal versions, it is apparent that the boundary matrices ![]() are crucial in
are crucial in
solving the boundary values of the field intensities. With given model property tensors ![]() and interface
and interface
normal![]() , the boundary values can be directly calculated through the boundary matrix. This mathematical merit is not possessed by the implicit boundary equations given in the previous section when dealing with the arbitrary interface between two anisotropic rocks.
, the boundary values can be directly calculated through the boundary matrix. This mathematical merit is not possessed by the implicit boundary equations given in the previous section when dealing with the arbitrary interface between two anisotropic rocks.
In isotropic media, ![]() and
and![]() , and Equation (14b) is changed into
, and Equation (14b) is changed into
![]() . (18)
. (18)
This indicates that if there is no difference in model properties, the boundary matrix becomes a unit matrix ![]() due to
due to![]() . It indicates that the field intensity maintains its continuity when the net external current source is zero at the interface
. It indicates that the field intensity maintains its continuity when the net external current source is zero at the interface![]() .
.
At the air-earth interface, we have ![]() (pure imaginary value) and
(pure imaginary value) and![]() , the boundary matrix Equation (14b) becomes
, the boundary matrix Equation (14b) becomes
![]() (19)
(19)
Specifically, if the electric permittivity of the earth is the same as air, i.e.![]() , Equation (19) is reduced to
, Equation (19) is reduced to
![]() (20)
(20)
It indicates that if the electric field ![]() is real
is real ![]() and the net external current source continues at the interface, then the real and imaginary boundary values on the “+” side are given by
and the net external current source continues at the interface, then the real and imaginary boundary values on the “+” side are given by ![]() and
and ![]() respectively. This shows that the imaginary values of the field intensity on the “+” side are not zero cross the interface.
respectively. This shows that the imaginary values of the field intensity on the “+” side are not zero cross the interface.
4. Explicit Tangential Version
In contrast to the implicit formulae given by Equations (3) and (6), the explicit normal versions of the boundary conditions, e.g. Equations (13) and (18), do not directly indicate continuity of the tangential components of electromagnetic field intensities ![]() at an interface due to absence of the tangential vectors of an interface. In order to overcome this weakness, three perpendicular interface vectors
at an interface due to absence of the tangential vectors of an interface. In order to overcome this weakness, three perpendicular interface vectors ![]() are introduced at a point of the interface (see Figure 1):
are introduced at a point of the interface (see Figure 1):
![]() (21)
(21)
Here, the angles ![]() are calculated by
are calculated by
![]() (22)
(22)
where ![]() defines topography of an arbitrary interface. According to spline theory [7] ,
defines topography of an arbitrary interface. According to spline theory [7] , ![]() may be approached by a 2-D spline interpolation:
may be approached by a 2-D spline interpolation:
![]() . (23)
. (23)
The coefficients ![]() are defined in the subdomain
are defined in the subdomain ![]() and determined by the known regularly-gridded or scattered samples of
and determined by the known regularly-gridded or scattered samples of ![]()
![]() . According to the spline theory, Equation (23) guarantees the continuity of the interface vectors
. According to the spline theory, Equation (23) guarantees the continuity of the interface vectors ![]() at every point of the interface. Equations (21) and (22) indicate that the interface vectors
at every point of the interface. Equations (21) and (22) indicate that the interface vectors ![]() change with the interface topography
change with the interface topography![]() . If it is flat
. If it is flat![]() , then the interface vectors
, then the interface vectors ![]() become the Cartesian vectors
become the Cartesian vectors ![]() or
or![]() , which are the constant directions of the x-, y- and z-axis. Consequently, the electromagnetic field intensities may be expressed by either the Cartesian or interface-vector forms, i.e.
, which are the constant directions of the x-, y- and z-axis. Consequently, the electromagnetic field intensities may be expressed by either the Cartesian or interface-vector forms, i.e.
![]() . (24)
. (24)
Therefore, Equation (3) can be rewritten in the following forms:
![]() (25)
(25)
Combining these two equations yields
![]() , (26)
, (26)
where
![]() (27)
(27)
Substituting Equation (26) into Equation (24) results in
![]() (28)
(28)
and
![]() (29)
(29)
where
![]() . (30)
. (30)
Upon comparing Equations (29) and (30) with Equations (13) and (14), it is apparent that Equation (29) displays the same explicit linear matrix form as Equation (13) but with different boundary matrices![]() ; the boundary matrix
; the boundary matrix ![]() given by Equation (30) involves two tangential vectors
given by Equation (30) involves two tangential vectors![]() , whereas the previous matrix
, whereas the previous matrix ![]() given by Equation (14) does not. Therefore, it can be deduced that Equation (30) is another form of Equation (14), and given the term “explicit tangential versions” of the boundary conditions to distinguish from the explicit normal versions.
given by Equation (14) does not. Therefore, it can be deduced that Equation (30) is another form of Equation (14), and given the term “explicit tangential versions” of the boundary conditions to distinguish from the explicit normal versions.
Similarly, substituting ![]() into Equation (29) and then applying the boundary conditions
into Equation (29) and then applying the boundary conditions
![]() in the reference model tensor
in the reference model tensor![]() ,
, ![]() or
or![]() ,
, ![]() , the following explicit tangential versions of the boundary conditions are obtained:
, the following explicit tangential versions of the boundary conditions are obtained:
![]() (31)
(31)
Equations (29) and (31) can be changed for magnetic field intensity by symbol replacements:
![]() (32)
(32)
![]() (33)
(33)
These equations correspond to Equations (4) and (8), or Equations (16) and (17).
At an isotropic interface, ![]() and
and![]() . Thus, Equation (30) can be simplified to
. Thus, Equation (30) can be simplified to
![]() , (34)
, (34)
At the air-earth interface, Equation (30) becomes
![]() , (35)
, (35)
and if the media possesses the same electric permittivity as air, i.e.![]() , Equation (35) is changed into
, Equation (35) is changed into
![]() . (36)
. (36)
5. Equivalence of the Different Version
The two integrated and explicit boundary conditions formulated above demonstrate a matrix ![]() that can be calculated by either Equation (14) or Equation (30). Although the two versions are derived from the same implicit formulae, e.g. Equations (3) and (7), the boundary matrices
that can be calculated by either Equation (14) or Equation (30). Although the two versions are derived from the same implicit formulae, e.g. Equations (3) and (7), the boundary matrices ![]() appear to differ. From a mathematical perspective, the different versions, i.e. explicit normal and tangential versions, as well the original implicit equations should be equivalent to each other because of uniqueness of the boundary values.
appear to differ. From a mathematical perspective, the different versions, i.e. explicit normal and tangential versions, as well the original implicit equations should be equivalent to each other because of uniqueness of the boundary values.
Multiplying the matrix ![]() to Equation (13), and then applying the factorization of the boundary matrix
to Equation (13), and then applying the factorization of the boundary matrix![]() , the matrix form of Equation (3) is obtained from Equation (13):
, the matrix form of Equation (3) is obtained from Equation (13):
![]() (37)
(37)
Similarly, Equations (15), (16) and (17) can be changed into Equations (7), (4) and (8) respectively. These formulations show that the explicit normal versions are equivalent to two common implicit boundary equations.
Applying the perpendicular properties of the interface vectors to Equation (30), e.g.![]() ,
, ![]() and
and![]() , the following equations are obtained:
, the following equations are obtained:
![]() (38)
(38)
Substituting these identities into Equation (29) yields
![]() (39)
(39)
These equations indicate continuity of the tangential components and discontinuity of the normal components of the electric field intensities. It proves that the explicit tangential versions are also equivalent to two common implicit boundary conditions.
Note that the three interface vectors given by Equation (21) satisfy the following equation
![]() . (40)
. (40)
Accordingly, equation (30) may be rewritten as follow
![]() (41)
(41)
which is the same as Equation (14b). Similarly, substituting Equation (40) for Equations (34), (35) and (36) respectively, they become Equations (18), (19) and (20). Therefore, the explicit tangential versions are equivalent to the explicit normal versions and vice versa as Equation (41) are reversible. Specifically, when the two media have the same electric permittivity![]() , i.e.
, i.e.![]() , Equation (41) is changed into
, Equation (41) is changed into
![]() (42)
(42)
This shows the small imaginary value ![]() when a low frequency is considered.
when a low frequency is considered.
6. Transformation of Boundary Values
The boundary element theory has shown that if there is not any external current source ![]() and
and ![]() in a homogeneous medium, the electromagnetic field intensities
in a homogeneous medium, the electromagnetic field intensities ![]() in the medium domain
in the medium domain ![]() may be expressed by the following boundary integral [8] :
may be expressed by the following boundary integral [8] :
![]() . (43)
. (43)
Here, ![]() is the Greens function of the homogeneous medium,
is the Greens function of the homogeneous medium, ![]() takes the values of 1.0, 0.5 and
takes the values of 1.0, 0.5 and ![]() responses to
responses to![]() ,
, ![]() (smooth) and
(smooth) and ![]() (not smooth) respectively, and
(not smooth) respectively, and ![]() is the corner angle at
is the corner angle at![]() . This equation indicates that calculation of the electromagnetic field intensities
. This equation indicates that calculation of the electromagnetic field intensities ![]() in the homogeneous medium require not only the boundary values of the field intensities
in the homogeneous medium require not only the boundary values of the field intensities ![]() but also the normal derivatives
but also the normal derivatives![]() . The boundary element method based on Equation (43) [8] [9] offers a tool to find the boundary values
. The boundary element method based on Equation (43) [8] [9] offers a tool to find the boundary values ![]() or
or ![]() with the known field intensities
with the known field intensities ![]() or normal derivatives
or normal derivatives![]() . Unfortunately, in most of electromagnetic modeling cases, neither the boundary values of the field intensities
. Unfortunately, in most of electromagnetic modeling cases, neither the boundary values of the field intensities ![]() nor the normal derivatives
nor the normal derivatives ![]() are known. However, if the field intensities
are known. However, if the field intensities ![]() in the connected domain
in the connected domain ![]() are given or going to be solved, the normal derivatives
are given or going to be solved, the normal derivatives ![]() at the interface can be calculated by numerical differentiations with the known or solved field intensities
at the interface can be calculated by numerical differentiations with the known or solved field intensities![]() . In this case, application of Equation (43) needs transformations of the boundary values from
. In this case, application of Equation (43) needs transformations of the boundary values from ![]() to
to![]() . Apparently, the integrated and explicit boundary conditions presented in the previous sections are directly applicable to these transformations, e.g. substituting Equations (13) and (16) for the second term of the right-hand-side surface integral of Equation (43) achieves the transformation of the boundary values
. Apparently, the integrated and explicit boundary conditions presented in the previous sections are directly applicable to these transformations, e.g. substituting Equations (13) and (16) for the second term of the right-hand-side surface integral of Equation (43) achieves the transformation of the boundary values ![]() into
into![]() . For transforming the normal derivatives
. For transforming the normal derivatives ![]() into
into![]() , one may follow the same methodology as described in the previous sections and obtain the integrated and explicit boundary conditions of the normal derivatives.
, one may follow the same methodology as described in the previous sections and obtain the integrated and explicit boundary conditions of the normal derivatives.
We calculate ![]() on both sides of Equation (1) and obtain
on both sides of Equation (1) and obtain
![]() (44)
(44)
which give zero divergences
![]() (45)
(45)
Applying Equations (44) and (45) to an interface of two anisotropic media, we obtain the boundary conditions of the partial derivatives:
![]() (46)
(46)
and
![]() (47)
(47)
Therefore, we have the following integrated and explicit versions of Equations (46) and (47):
![]() , (48)
, (48)
![]() , (49)
, (49)
where the components of matrices ![]() and
and ![]() are given by
are given by
![]() (50)
(50)
Applying Equations (13), (16), (48) and (49) for Equation (43), one can fulfill the transformations of the boundary values from the domain ![]() into
into![]() , in which the field intensities
, in which the field intensities ![]() are going to be solved and the normal derivatives
are going to be solved and the normal derivatives ![]() can be calculated with the given interface topography
can be calculated with the given interface topography ![]() and its nearby field intensities
and its nearby field intensities![]() . Particularly, after achieving the transformations of the boundary values, the boundary integral
. Particularly, after achieving the transformations of the boundary values, the boundary integral ![]() in Equation (43) can be approached by the boundary element method [9] that results in
in Equation (43) can be approached by the boundary element method [9] that results in ![]() (total points of the interface) linear equations of the field intensity
(total points of the interface) linear equations of the field intensity ![]() or
or![]() . These equations are considered as “the boundary equations” of the field intensities
. These equations are considered as “the boundary equations” of the field intensities ![]() and independently complementary to the linear equations yielded by other numerical approach applied to the domain
and independently complementary to the linear equations yielded by other numerical approach applied to the domain![]() , e.g. finite-difference or finite-element method. Therefore, the numerical computations of the field intensities
, e.g. finite-difference or finite-element method. Therefore, the numerical computations of the field intensities ![]() are implemented only in the domain
are implemented only in the domain ![]() and have nothing relating to
and have nothing relating to![]() , so that the computational dimensions are significantly reduced. These developments of hybrid methods are beyond the topic of this paper and will be given in our future articles.
, so that the computational dimensions are significantly reduced. These developments of hybrid methods are beyond the topic of this paper and will be given in our future articles.
7. Synthetic Examples
In order to demonstrate possible applications of the integrated and explicit versions of the boundary conditions, synthetic experiments of a hill and a ridge model have been conducted (see Figure 2 and Figure 4). These models may represent the Earth’s surface, or seafloors, or subsurface interfaces of rocks. The synthetic experiments were only carried out using electric fields ![]() with the explicit normal versions due to the similarity between magnetic fields
with the explicit normal versions due to the similarity between magnetic fields ![]() and electric fields
and electric fields![]() , and the equivalence of the two explicit versions. In these experiments, the frequency of 0.1 Hz and an external plane-wave source at infinity were considered
, and the equivalence of the two explicit versions. In these experiments, the frequency of 0.1 Hz and an external plane-wave source at infinity were considered![]() , and the hill and ridge interfaces were approximated by Equation (23) using regularly-gridded samples of the interface topographies. Above the interface, the conductivity tensor
, and the hill and ridge interfaces were approximated by Equation (23) using regularly-gridded samples of the interface topographies. Above the interface, the conductivity tensor ![]() was assigned to the air
was assigned to the air ![]() and an anisotropic medium
and an anisotropic medium ![]() respectively. Below the interface, a different anisotropic medium was applied
respectively. Below the interface, a different anisotropic medium was applied![]() . These two media have the same electric permittivity as air. In addition, we assumed the boundary values of the electric field intensity
. These two media have the same electric permittivity as air. In addition, we assumed the boundary values of the electric field intensity ![]() in the air-domain are known, e.g.
in the air-domain are known, e.g.![]() ,
, ![]() , which represents the observed data on the Earth’s surface or seafloor from a practical measurement [10] , or the numerical solution from the boundary element method [8] [9] . The new integrated and explicit versions enable us to directly recover the boundary values
, which represents the observed data on the Earth’s surface or seafloor from a practical measurement [10] , or the numerical solution from the boundary element method [8] [9] . The new integrated and explicit versions enable us to directly recover the boundary values ![]() under the ground or seafloor. It is possible to combine the transformed boundary values with other numerical method in
under the ground or seafloor. It is possible to combine the transformed boundary values with other numerical method in ![]() and perform the forward modeling or tomographic inversion without the air or seawater domain.
and perform the forward modeling or tomographic inversion without the air or seawater domain.
Figure 2 displays the synthetic results at the air-earth interface of a hill. Three components of the boundary values ![]() are plotted and show discontinuities throughout the vertical components
are plotted and show discontinuities throughout the vertical components![]() , and continuity in the horizontal components
, and continuity in the horizontal components ![]() at the flat portions of the interface due to
at the flat portions of the interface due to ![]() and
and![]() . Discontinuity of
. Discontinuity of ![]() in the hill area arises when
in the hill area arises when ![]() and
and![]() . It also shows that the imaginary parts
. It also shows that the imaginary parts ![]() are very small
are very small ![]() due to the low frequency (0.1 Hz) and same electric permittivity
due to the low frequency (0.1 Hz) and same electric permittivity ![]() of the two media. Therefore, these imaginary parts are often ignored in most magnetotelluric measurements [1] .
of the two media. Therefore, these imaginary parts are often ignored in most magnetotelluric measurements [1] .
Figure 3 demonstrates three components of the electric current density![]() , whose real
, whose real ![]() and imaginary values
and imaginary values ![]() display the conduction and displacement current densities respectively. These diagrams indicate that the conduction current density disappears in air
display the conduction and displacement current densities respectively. These diagrams indicate that the conduction current density disappears in air ![]() due to zero
due to zero
conductivity ![]() and displacement current density occurs
and displacement current density occurs ![]() because of non-zero electric permittivity
because of non-zero electric permittivity![]() , whilst the normal total current densities remain unchanged
, whilst the normal total current densities remain unchanged ![]() and the tangential total current densities vary
and the tangential total current densities vary![]() . These characteristics are predictable from the implicit boundary equations.
. These characteristics are predictable from the implicit boundary equations.
Figure 4 demonstrates the synthetic results of a ridge interface that connects two anisotropic media. Similar characteristics to those in Figure 2 are again observed, including discontinuities throughout the vertical components![]() , continuity in the x-components
, continuity in the x-components ![]() except in the ridge area where
except in the ridge area where![]() , and continuity in the y- component
, and continuity in the y- component ![]() in all areas due to
in all areas due to ![]() (see the middle panel in Figure 4). Figure 5 demonstrates three components of the electric current density
(see the middle panel in Figure 4). Figure 5 demonstrates three components of the electric current density![]() , which indicate that the conduction and displacement current densities exist in the two media, and the tangential current densities
, which indicate that the conduction and displacement current densities exist in the two media, and the tangential current densities ![]() differ from
differ from ![]() because of two different conductivities, but the normal currents
because of two different conductivities, but the normal currents ![]() remain the same regardless of the interface topography.
remain the same regardless of the interface topography.
8. Conclusions
Two new integrated and explicit boundary conditions, termed the “normal” and “tangential” versions, have been presented in this paper for electromagnetic fields at an arbitrary interface between two anisotropic media. These two versions both achieve combination of two implicit boundary equations into a single explicit linear matrix form, and consistently reveal that the boundary values are linked by a 3 × 3 boundary matrix dependent on the interface topography and electric conductivity or magnetic permeability tensors of the media. The normal version shows that the boundary matrix is calculated with the known normal of the interface and model property tensors; while the tangential version indicates that the boundary matrix requires two perpendicular tangential vectors besides the normal of the interface. However, despite these differences, the mathematical equivalence of the two new versions to each other, as well as to the standard implicit boundary conditions is demonstrated. With known normal ![]() of an interface, the explicit normal version is more compact and efficient compared to the explicit tangential version because the two perpendicular tangential vectors
of an interface, the explicit normal version is more compact and efficient compared to the explicit tangential version because the two perpendicular tangential vectors ![]() are not required. With a given interface
are not required. With a given interface![]() , there is no difference between the two versions in computational efficiency as the tangential vectors
, there is no difference between the two versions in computational efficiency as the tangential vectors ![]() and normal
and normal ![]() must be calculated from the interface topography function
must be calculated from the interface topography function![]() .
.
The synthetic examples of a hill and a ridge interface demonstrate possible applications in conversions of the boundary values, and capability of the new versions to arbitrary interfaces that may involve complex topography and anisotropic rocks. These results numerically show continuity of the tangential components and discontinuities of the normal components of electromagnetic field intensities, and continuity of the normal components and discontinuities of the tangential components of electric current densities across the air-earth interface and the boundary of two anisotropic rocks. These synthetic examples also demonstrate that the boundary values of the
field intensities may change with alterations in topography of the interface, electric conductivity and permittivity tensors, or magnetic permeability tensors. It is shown that with help of the new integrated and explicit versions, the unknown boundary values can be obtained by simply multiplying a boundary matrix with the known boundary values. Therefore, it provides a more straightforward and easier method to transform the boundary values from one domain to another. It is greatly helpful to not only extrapolation of electromagnetic fields with the boundary element approach, but also combination of the boundary element approach with other numerical methods, such as finite-difference, finite-element and integral equation method, because the boundary element approach with the transformed boundary values can offer complementary linear equations to these numerical methods, so that the numerical computations remain in the interesting model domain and the computational dimensions are significantly reduced.
Acknowledgements
This work was supported by a Discovery Project (DP1093110) of the Australia Research Council. The authors thank Mr. Craig Patten for his assistance in using high-performance computing facility at e Research SA in Australia.