A Neuron Model with Dendritic Nonlinearity for Predicting the Influence of Overreaction in Shanghai Stock Market ()
1. Introduction
One way used to predict the extent of stock-market weak-form efficiency is through testing for the effect of overreaction, i.e. the degree to which investors overreact to good or bad news causing share prices to deviate from their equilibrium level. In particular, securities suffering abnormally-low returns in the past (losers) will experience relatively higher returns, whereas shares performing well in the past (winners) will do less well in the future.
De Bondt and Thaler are the forerunners in the study of the effect of overreaction on the stock markets. They have used the data of stock mark in the US between 1926 and 1982 to analyze whether investors overreact, and identified a long-term reversion in stock prices due to the investors’ irrational behavior (De Bondt & Thaler, 1985) . Lehmann (1990) has used data from the US stock market between 1965 and 1989 to identify the factors that have reversed the market in a short time-interval but could not correlate short-term profitability with overreaction, suggesting that market reversal was a result of short-term pressures on prices in short term or the lack of liquidity (Lehmann, 1990) .
To build the stock market value, one of the best ways is to use expert systems with Artificial Neural Networks (ANN), which can easily adapt the changes of the stock market. It is observed that in most of the cases ANN models give better result than other methods. However, there have been a few studies on using the ANN for stock market: Generalized version of ARCH model, Generalized ARCH (GARCH) model (Bollerslev, 1986) , Exponential GARCH (EGARCH) model (Nelson, 1991) , Dynamic Architecture for Artificial Neural Networks (DAN2) and so on. Since the late 1990s, Chinese scholars have studied overreaction on stock mark in China. Zhang Renji, Zhu Pingfang, and Wang Huaifang (1998) have found a decreasing trend in winner portfolio. Zhu Shaoxing (2000) has conducted that overreaction did not affect the Shenzhen stock market. Song Xianzhong and Tang Sheng (2006) have conducted an empirical study on overreaction and scale effect on the corporations listed in A-share market in Shanghai. In our previous study, Shanghai stock market trading data from January 2007 to June 2011 have suggested an overreaction on the stock market (Hu Lin, Sha Zijun, Liu Xiuyi, & Chen Wenjun, 2013) . In recent years, there have been a growing number of studies about movements of various kinds on stock market. Both academic researchers and practitioners have made tremendous efforts to predict the future movements of the stock markets. Zhang Yanqing and Wan Xuhui (2007) have developed a new ANN based on Fuzzy Interval Neural Network. Zhu Xiaotian, Wang Hong, Xu Li, and Li Huaizu (2008) have found trading volume can improve the prediction performance of neural networks by using basic and augmented neural network models. Liao Zhe and Wang Jun (2010) have identified some results on the global stock indices, using stochastic time effective neural network model.
In this paper, stock market data from 2004 to 2014 are analyzed to verify the overreaction in Shanghai stock market once again, and the neuron model with dendritic nonlinearity, for the first time, is used to fit and predict the trends of overreaction. This new approach aims to provide a novel solution for future research, as well as a valuable tool for business implementation.
The remaining sections of this paper are organized as follows: Section 2 gives the sample selection and test methods; Section 3 introduces the models in this paper and Section 4 shows the experiments and results. The final section gives the conclusion and recommendations for future researches. This study will make contribution not only to the ANN research but also to the business implementations of stock market.
2. Empirical Study on the Overreaction
2.1. Sample Selection and Test Methods
This paper extracts 200 stocks, at random, from the Shanghai stock market, covering the time-interval from January 2004 to October 2014 including the daily closing prices. Considering stock dividends and rights offerings, the returns of each stock is calculated on the price excluding rights. The stock’s closing price remains the same for stocks pending suspension. Based on the sequence of the level of cumulative abnormal returns in formation period, the top 20 stocks constitute the winner portfolio, and the loser portfolio is composed of the lowest 20 stocks.
2.2. Sorting Methods in the Formation Period
The formation period in the paper is divided into 3 months, 6 months, 12 months, 18 months and 24 months; the corresponding test period is separated by 1 month, 3 months, 6 months, 12 months, 24 months and 36 months. If the reference time, the length of formation period and the length of test period are set to T0, T1 and T2, respectively, (T0 − T1, T0) is the formation period, and (T0, T0 + T2) is the test period. If the reference time is constant, more combinations between the formation period and the test period may be attained. The formations period and the test period, in these combinations, do not overlap, but the current test period and the next formation period may overlap.
The calculation of excess returns uses incorporates a marketing adjustment, as proposed by De Bondt, Richard Thaler and Paul Zarowin. The formula is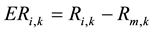 ;
; 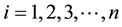
Ri,k is yield of stock I in k month.
Rm,k is yield of market in k month.
Cumulative excess return for stock I in the formation period is 
2.3. The Test Methods in Test Period
On the basis of the data sequence of the cumulative abnormal returns levels in the formation period, the top 20 stocks make the winner portfolio and the lowest 20 stocks make the loser portfolio. Thus, the calculated average abnormal monthly returns for each combination are given by:
 (1)
(1)
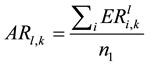 (2)
(2)
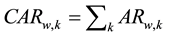 (3)
(3)
 (4)
(4)
Here, ARw,k is the average abnormal monthly returns of the winner portfolio, ARl,k is the average abnormal monthly returns of the loser portfolio, CARw,k is the average cumulative abnormal returns of the winner portfolio, and CARl,k is the average cumulative abnormal returns of the loser portfolio.
3. Neuron Model for Predicting
In 1943, McCulloch and Pitts have proposed a neuron model, which is recognized as the basic computation units for neural network (McCulloch & Pitts, 1943) . However, in this model, the dendrites are only taken as mere weight, thus an independent McCulloch-Pitts model (Figure 1) can’t deal with the complex nonlinear problem, for example EX-OR problem.
However, with the gradual in-depth study, it has been proved that the dendrites participate into the computation of neuron instead of mere transmitting signals (Kitajima & Hara, 1987; Koch, Poggio, & Torre, 1982 ; London & Häusser, 2005) .
3.1. Neuron Model with Dendritic Nonlinearity
In 2000, Tang et al. have proposed a neuron model based on dendritic mechanism ( Tang, Tamura, Kuratu, Ishizuka, & Tanno, 2000 ; Tang, Tamura, Ishizuka, & Tanno, 2000 ). Moreover, it also holds the movement direction selection function based on time difference (Tamura, Tang, & Ishii, 2001) . The computational ability of this model can be expressed as logical operation of AND, OR and NOT. Moreover, in order to reduce computational time and generalize the neuron model into a continuum of values between 1 and 0, Tang et al. have proposed a novel neuron model, called Neuron Model with Dendritic Nonlinearity (NMDN), which uses the multiplication and addition to replace the logical AND and OR, respectively (Todo, Tang, Todo, Ji, & Yamashita, 2014 ). As shown in Figure 2, it is NMDN used in this paper.
![]()
Figure 2. Neuron model with dendritic nonlinearity.
In NMDN, the synaptic function is expressed by the sigmoid function. The output of the synapse whose address is from i-th 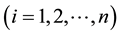 input to j-th
input to j-th 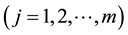 branch is given by
branch is given by
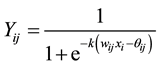 (5)
(5)
where 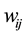 and
and 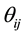 are the connection parameters, and k is a positive constant. If k is large enough, the sigmoid function becomes similar with step function.
are the connection parameters, and k is a positive constant. If k is large enough, the sigmoid function becomes similar with step function.
The synaptic output on the branch performs a simple multiplication. The output of j-th branch is given by
 (6)
(6)
Moreover, as mentioned above, the summation on signals sent from the dendrites is expressed by
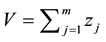 (7)
(7)
Finally, the function of soma is also described through a sigmoid function as following
![]() (8)
(8)
where the ![]() is taken as a positive constant, and the
is taken as a positive constant, and the ![]() is taken as a threshold.
is taken as a threshold.
3.2. Learning Algorithm
NMDN is a feed-forward network with continuous functions, all differential. Therefore, the gradient descent learning algorithm is used as the learning procedure. Learning is aimed to reduce the difference between the output and the target vector by modifying ![]() and
and ![]() of synapses.
of synapses.
The error between the target vector and the output vector can be expressed by following
![]() (9)
(9)
where the T is taken as the target, and the O is taken as the output.
During the learning procedure, these parameters are modified to decrease the error, and the connection parameters should be corrected according to the following formulas:
![]() (10)
(10)
![]() (11)
(11)
where![]() , called the learning constant, is a positive constant.
, called the learning constant, is a positive constant.
![]() (12)
(12)
![]() (13)
(13)
where ![]() and
and ![]() are the corrected values, and
are the corrected values, and ![]() and
and ![]() are their current value. Thus, the partial differentials of E with respect to
are their current value. Thus, the partial differentials of E with respect to ![]() and
and ![]() can be presented respectively as:
can be presented respectively as:
![]() (14)
(14)
![]() (15)
(15)
4. Experiments & Results
4.1. Empirical Result of Overreaction
The applied method, in this study, provides substantial results in Table 1. The average cumulative abnormal returns (CAR) of loser portfolio have been greater than that of winner portfolio in the 18 months formation period in Figure 3. The result is basically consistent with our former study. Overreaction is evident in the Shanghai stock market during the studied interval. Combing the results presented in Table 1 and Figure 3, the difference in CAR between the loser and winner portfolio reaches a maximum of 17.36% at six month from the beginning of the test period. Furthermore, the degree of overreaction gradually decreases with time, and finally has gone to disappear. Moreover, one may get significant arbitrage profit on the overreaction period by buying the stocks of loser portfolio at an early stage and selling the ones of winner portfolio.
However, the data listed in Table 1 is not enough to train the NMDN on a more refined level. In order to display the alteration between winner and loser portfolios more precisely, Figure 4 shows the curve of a 94-month test period with the step of one month. In Figure 4, the curve of L-W goes to under 0, meaning that the overreaction effect disappears. Furthermore, Figure 5 presents the difference between loser and winner portfolios’ AR. The NMDN here is used to predict the difference of CAMR and then assess the CAR curve of L-W.
4.2. Parameters of NMDN
As mentioned in Section 3, there are some parameters in NMDN need to be set up. Altering these parameters have distinct influence on the training and predicting. However, there has been no clear criterion to determine which values of parameters can maximize the ability of NMDN. Table 2 shows the mean squared error (MSE), epoch of learning (Epochs), learning constant (η), threshold (γ), K, Ksoma and Branch in this paper, acquired empirically.
However, in order to train NMDN for prediction, the input data of NMDN is defined in Table 3. In this paper, AR is selected as input data for NMDN, and n-months data, indicated as the step, is used for predicting the data of (n + 1)-month. The NMDN has been trained 50 times on each step, respectively.
![]()
Table 1. CAR of the winner and loser portfolios.
![]()
Figure 3. CAR curves of 18-month formation period.
![]()
Figure 4. CAR curves of 18-month formation period for 94 months.
![]()
Figure 5. The difference between loser portfolio’s AR and winner portfolio’s.
![]()
Table 2. NMDN parameters applying for training and prediction.
4.3. The Result of Prediction
Figure 6 shows the average prediction curve for each step. The curve, using 3 months input data to predict the data of following month, deviates from the standard curve demonstrating that there may be no significant relationship between them. Moreover, although it performs not so well on using the data of 4, 5 and 6 months to predict the data of the following month, NMDN has succeeded in predicting the decreasing tendency of L-W. In order to quantify the fitness of prediction, the goodness of fit, Rnew, is introduced to compare the performance on different steps in Table 4. Higher Rnew values indicate that the model fits the data better.
Combining Figure 6 with Table 4, it becomes evident that Rnew turns larger with increasing steps. The growth of Rnew indicates that with increasing steps, the correlation between the data of first n-month and following month greatly improves. This result indicates a possible connection between on the first n-month and following months.
5. Conclusions
In this paper, the overreaction effect on the Shanghai stock market is confirmed once again by using more recent data. The influence of overreaction occurring since 2007 can be found to turn to gradually diminish and finally becomes obsolete.
![]()
Figure 6. Average prediction result on different steps.
![]()
Table 4. The goodness of fit, Rnew.
A neuron model with dendritic nonlinearity (NMDN) is used here, for the first time, to predict the tendency of overreaction. The first n-months’ data are treated as input data to predict the following month’s data. The result indicates that the neuron model possesses huge computational ability and succeeds in predicting the overreaction tendency. Moreover, with the increase of steps, the correlation between the data of the first n-month and the following month turns to be improved. Moreover, NMDN provides another new approach for the researchers.
For the future work, the research will be focused on the accuracy of prediction by using NMDN.