Effect of Initial Stress on Wave Frequencies of Elastic Solid with Rotation ()
1. Introduction
The analysis of the dynamic problems of elastic bodies is an important and interesting research field for engineers and scientists. Toudeshky, et al. [1] investigated sound transmission into a thick hollow cylinder with the fixed end boundary condition. Hua et al. [2] investigated axisymmetric vibrations of a viscous-fluid-filled piezoelectric spherical shell and the associated radiation of sound. Hasheminejad and Mirzaei [3] studied exact 3D elasticity solution for free vibrations of an eccentric hollow sphere. Buchanan and Liu [4] investigated analysis of the free vibration of thick walled isotropic toroidal shells. Jianqiao, Qiujuan and Shan [5] studied the wave propagation in non-homogeneous magneto-eletro-elatic hollow cylinders. Abd-Alla, et al. [6] studied the effect of non-homogeneity on the composite infinite cylinder of isotropic material. Add-Alla, and Abo-Dahb [7] investigated time-harmonic sources in a generalized magneto-thermo-viscoelastic continuum with and without energy dissipation. The rotation of a non-homogeneous composite infinite cylinder of orthotropic and isotropic material, and the thermal stresses in a rotating non-homogeneous orthotropic hollow cylinder has been investigated by El-Naggar, et al. [8] - [10] . In [11] , Abd-Alla et al. investigated the effect of the rotation on a non-homogeneous infinite cylinder of orthotropic material. Abd-Alla et al. [12] studied the propagation of S-wave in a non-homo- geneous anisotropic incompressible and initially stressed medium under influence of gravity field. Gupta and shukla [13] studied the effect of nonhomomgeneity on elastic-plastic transition in a thin rotating disk. Chatzigeorgiou, et al. [14] investigated homogenization problems of a hollow cylinder made of elastic material with discontinuous properties. Abd-Alla, et al. [15] [16] investigated the effect of the non-homogeneity on the composite infinite cylinder of isotropic and orthotropic materials. Buchanan and Yii [17] studied the effect of symmetrical boundary conditions on the vibration of thick hollow cylinders. Ding, et al. [18] [19] studied the elastodynamic solution of a non-homogeneous orthotropic hollow cylinder, and a solution of a non-homogeneous orthotropic cylindrical shell for a xy-symmetric plane strain dynamic thermoelastic problem. Inclusion of arbitrary shape in magneto-electro-elastic composite materials has been investigated by Wang and Shen [20] . Hou et al. [21] obtained the analytical solution for the axisymmetric plane strain electro elastic dynamics of a non- homogeneous piezoelectric hollow cylinder. Hearmon [22] studied the elastic constants of anisotropic material. Hou and Leung [23] further studied the corresponding problem of magneto-electro-elastic hollow cylinders.
In this paper, we study the effect of initial stress on the radial vibrations of elastic hollow cylinder with rotation of a cylindrical region hollow of radius a, b with different boundary conditions (free-fixed-mixed). The one- dimensional equation of elastodynamics for isotropic media is solved. The numerical results of the frequency equation are discussed and plotted graphically.
2. Formulation of the Problem
In this section, we derive the analytical formulation of the problem in cylindrical coordinates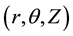 
with the z-axis coinciding with the axis of the cylinder. We consider the strains symmetric about the z-axis. We have only the radial displacement
, 
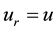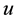is a function of 
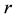and 
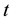only, the circumferential displacement 
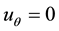and the longitudinal displacement
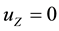, which are independent of 
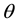and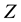
. The stresses-displacement relation for cylindrically isotropic material in one dimension is in the form:
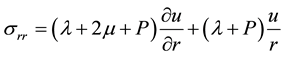
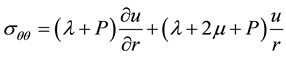. (1)
The dynamical equation in the direction r, and taking the rotation term about z-axis as a body force is given by:
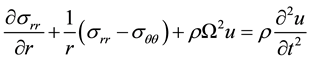(2)
where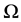 
is the uniform angular velocity and 
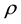is the density of the cylinder material.
Substituting from Equation (1) into Equation (2) we obtain:
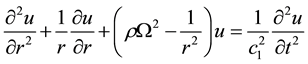(3)
where
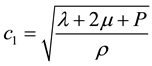
where P is the initial stress.
3. Solution of the Problem
In this section, we obtain the analytical solution of above problem for a cylindrical region of inner radius a and outer radius b with different boundary conditions (free-fixed-mixed) by taking the harmonic vibrations. We simplify the function ![]()
into Equation (3) as follows:
![]()
(4)
where ![]()
is the natural frequency of the vibrations.
Substituting from Equation (4) into Equation (3) we get:
![]()
(5)
where
![]()
.
The Equation (5) is called the homogeneous Bessel equation which its general solution is known and takes the form:
![]()
(6)
where A and B are arbitrary constants and ![]()
and ![]()
denote Bessel’s functions of the first kind.
Substituting in Equation (1) from (6), the component of the stress ![]()
is given by:
![]()
(7)
We describe the different cases of the boundary conditions for the hollow cylinder in next section.
4. Boundary Conditions and Frequency Equation
In this case, we are going to obtain frequency equation for the boundary conditions of the hollow cylinder.
We consider the following transformations:
![]()
(8)
to make all the quantities dimensionless where W1 denote the frequency dimensionless.
4.1. Free Surface Traction
In this case, we are going to obtain frequency equation for the boundary conditions which specify that the free inner and outer surfaces of the hollow cylinder are free tractions from stresses.
![]()
(9)
Substituting from Equation (8) into Equation (7) and using Equation (9), we get two homogeneous linear equations in A and B:
![]()
(10)
Eliminating the constants A and B, we obtain the frequency equation in the form of a second order determinant as:
![]()
(11)
where
![]()
![]()
![]()
![]()
. (12)
From Equations (11), we reduce the frequency dimensionless equation in the form
![]()
. (13)
4.2. Fixed Surface
In this case, we are going to obtain a frequency equation for the boundary conditions which specify that the fixed inner and outer surfaces of the hollow cylinder are fixed from displacements.
![]()
(14)
which correspond to fixed inner and outer surfaces, respectively. From Equations (6) and (14), we obtain two homogeneous linear equations in A, B:
![]()
. (15)
Eliminating the constants A and B, we obtain the frequency equation in the form of a second order determinant as:
![]()
(16)
where:
![]()
. (17)
We reduce the frequency dimensionless equation in the form:
![]()
. (18)
4.3. Inner Surface Fixed and Outer Surface Free
In this case, we are going to obtain a frequency equation for the boundary conditions which specify that the inner surface fixed and outer surface free of the hollow cylinder are fixed and free from displacement and stress.
![]()
(19)
From Equations (6), (7) and (19), we obtain two homogeneous linear equations in A, B:
![]()
(20)
Eliminating the constants A and B, we obtain the frequency equation in the form of a second order determinant as
![]()
(21)
where
![]()
(22)
We reduce the frequency dimensionless equation in the form:
![]()
. (23)
4.4. Inner Surface Free and Outer Surface Fixed
In this case, we are going to obtain frequency equation for the boundary conditions which specify that the inner free surface and outer fixed surface of the hollow cylinder are free and fixed from stress and displacement.
![]()
(24)
From (6), (7) and (24), we obtain two homogeneous linear equation in A and B:
![]()
(25)
Eliminating the constants A and B, we obtain the frequency equation in the form of a second order determinant as:
![]()
(26)
where:
![]()
(27)
We reduce the frequency dimensionless equation in the form:
![]()
. (28)
5. Numerical Results and Discussion
Here, we shall investigate the dispersion relation given by (13), (18), (23), and (28) numerically. Since these equations is an implicit functional relation of natural frequency and the ratio h of the frequency equation, therefore one can proceed to find the variation of natural frequency with ratio h.
The program to evaluate the roots of the dispersion relations versus the different values of h for the first mode is made. We have adopted the following iterative procedure for numerical computations. For fixed value of h, we evaluate the determinant, present in the left hand side of above equations ((13), (18), (23) and (28)), for various values of the unknown quantity W, commencing with the initial value near zero and each time adding a fixed but small increment to that unknown quantity until the value of the determinant changes its signs. Then the bisection method is applied to locate the root correct to a chosen number of decimal places. With this roots the initial value, the procedure is repeated to find the next root.
For a given geometry and elastic constant of the cylinder (i.e., prescribed values of cij, the frequency equation is essentially an implicit transcendental function for the frequency parameter W. Thus, for fixed values of h, the frequency equation for different cases (free-fixed-mixed) is a function of W only. Values of were chosen as 0, 0.5, 1.0, 1.5 and 2.0. The results of frequency versus the ratio h are plotted in Figures 1-8 we use the data for isotropic material.
As an illustrative example, the elastic constants may be taken from Ding, et al. [18] for orthotropic material (Cobalt) in non-dimensional form
![]()
![]()
![]()
![]()
.
Figures 1-4 show that the variation of the non-dimensional frequency w with respect to the ratio h for different cases (free-surfaces, fixed-surfaces and mixed-surfaces) which it decrease with increasing of ratio h and the rotation W.
Figures 5-8 show that the variation of the non-dimensional frequency w with respect to the rotation W for different cases (free-surfaces, fixed-surfaces and mixed-surfaces) which it decrease with increasing of rotation and ratio h.
![]()
Figure 1. Frequency (w) versus the ratio (h) of homogeneous material (free traction surfaces) for different values of W.
![]()
Figure 2. Frequency (w) versus the ratio (h) of homogeneous material (fixed surfaces) for different values of W.
![]()
Figure 3. Frequency (w) versus the ratio (h) of homogeneous material (inner fixed and outer free surfaces) for different values of W.
![]()
Figure 4. Frequency (w) versus the ratio (h) of homogeneous material (inner free and outer fixed surfaces) for different values of W.
![]()
Figure 5. Frequency (w) versus the rotation (W) of homogeneous material (free traction surfaces) for different values of h.
![]()
Figure 6. Frequency (w) versus the rotation (W) of homogeneous material (fixed surfaces) for different values of h.
![]()
Figure 7. Frequency (w) versus the rotation (W) of homogeneous material (inner fixed and outer free surfaces) for different values of h.
![]()
Figure 8. Frequency (w) versus the rotation (W) of homogeneous material (inner free and outer fixed surfaces) for different values of h.
Next consideration is given to the relative change in the frequencies over a range of aspect (i.e., a/b) ratio of cylinder. This allows one to observe the frequency response for different rotation values of cylindrical shape. The results are presented as the variation in the dimensionless frequency W as a function of the aspect ratio of the cylinder, and are shown in Figures 1-8. All values were obtained by using half-interval method.
6. Conclusion
Harmonic vibrations of infinite elastic cylinder have been studied using a half-interval method. The governing equations in cylindrical coordinates are recorded for future reference. The non-dimensional frequency equations have been obtained under the effect of rotation W and ratio h. The numerical results of the natural frequency are obtained and discussed in detail for different cases. Comparisons are made with the results in the absence of rotation.