1. Introduction
General Markov chain only has locally strong Markov property, which is the main obstruction to solve the pro- blem of Markov chain constructing [1] [2] . The papers construct a strong Markov chain corresponding to its transition function using Ray-Knight compact method [3] [4] , which is named regular chain. The papers give an orbit construction of birth and death process [5] [6] . The papers solve the construction problem of two-sided birth and death process [3] -[11] . The papers prove that the appended points in the compacting and the points on the Martin entrance boundary are monogamy, under the condition of finite entrance boundary [12] -[14] . This paper makes a strong Markov process by Ray-Knight compacting, discusses its orbit nature and explains the significance probability of Kolmogorov forward and backward equations.
2. The Orbit Natures of Regular Chain
Assume 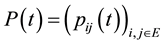 is a honest transition function on
is a honest transition function on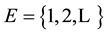 ,
, 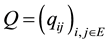 is its density func-
is its density func-
tion, 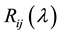 is its resolvent,
is its resolvent, 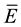 is the Ray-Knight compacting of
is the Ray-Knight compacting of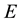 ,
,  and
and 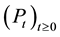 is the Ray re-
is the Ray re-
solvent and the semi-group correspondence, denote  as non-ramification point set,
as non-ramification point set,
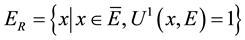 ,
, 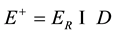 , then E is Borel algebras on
, then E is Borel algebras on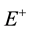 ,
, 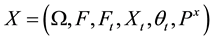 is the
is the
regular chain of correspondence to . Denote
. Denote 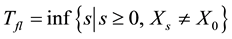 and
and 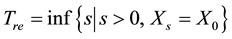
respectively as escape time and return time, by Blumenthal 0 - 1 law, for arbitrary![]() ,
, ![]() or 1,
or 1,
![]() or 1, if
or 1, if![]() , x is called absorption state, if
, x is called absorption state, if![]() ,
, ![]() is called sojourn state, if
is called sojourn state, if![]() ,
, ![]() is called regular state, if
is called regular state, if![]() ,
, ![]() is called temporary state.
is called temporary state.
Theorem 1 Let![]() , then
, then
(1) ![]() is a regular state,
is a regular state,
(2) on![]() , the distribution of escape time
, the distribution of escape time ![]() is the exponential distribution of
is the exponential distribution of![]() ,
,
(3) on![]() ,
, ![]() and
and ![]() is mutual independent.
is mutual independent.
(4) if![]() , for arbitrary
, for arbitrary![]() ,
,![]() .
.
Proof (1) Assume ![]() is not a regular state, then
is not a regular state, then![]() . for arbitrary
. for arbitrary![]() , it is easy to check
, it is easy to check![]() , and when
, and when![]() ,
, ![]() , thus
, thus
![]() ,
,
this is a contradictory proposition.
(2) The proof is same as Theorem
5 in
[15] .
(3) If ![]() or
or![]() , then
, then ![]() or
or![]() , the conclusion is true, if
, the conclusion is true, if![]() , for arbitrary Borel subset
, for arbitrary Borel subset ![]() and
and![]() ,
,
![]()
Let![]() , we have
, we have![]() .
.
then, on![]() ,
, ![]() ,
, ![]() and
and ![]() is mutual independent.
is mutual independent.
(4) If![]() , for arbitrary
, for arbitrary![]() , According to the strong Markov properties of
, According to the strong Markov properties of ![]() and (3), we can obtain that
and (3), we can obtain that
![]()
Give arbitrary![]() , and continuous function
, and continuous function ![]() on
on ![]() with
with![]() ,
,
![]()
but![]() , in addition,
, in addition,
![]()
thus,![]() .
.
Remark 1 (3), (4) in the Theorem 1 are equivalence with the Theorem
6 in
[15] , but it require![]() , do not incloude
, do not incloude![]() .
.
Remark 2 According to (2) in Theorem 1, ![]() is a temporary state, if and only if
is a temporary state, if and only if ![]() is a sojourn state of
is a sojourn state of
the regular chain![]() .
.
Definition 1 Let ![]() is the constant set of
is the constant set of![]() , the interval in
, the interval in ![]() is called i-interval of
is called i-interval of ![]()
Theorem 2 If![]() , then for arbitrary
, then for arbitrary![]() , we can get a stopping time squence
, we can get a stopping time squence![]() , with
, with![]() , when
, when![]() , we have
, we have![]() , when
, when![]() , we have
, we have![]() . And for arbitrary
. And for arbitrary![]() ,
,
![]()
For arbitrary![]() , denote
, denote ![]() as the number of
as the number of ![]() belong to
belong to![]() , we have
, we have
![]() .
.
Proof Let
![]() ,
,
![]() , ,
, ,
where ![]() are the stoping time of
are the stoping time of![]() . for arbitrary
. for arbitrary![]() , if
, if![]() , since
, since ![]() is right continuity,
is right continuity, ![]() , and
, and
![]()
then we have almost sure ![]() on
on![]() .
.
Since ![]() is strong Markov chain, and for arbitrary
is strong Markov chain, and for arbitrary![]() ,
,
![]()
then we have almost sure ![]() on
on![]() .
.
For arbitrary![]() , obviously
, obviously![]() , by Theorem
3.1 in
[15]
, by Theorem
3.1 in
[15]
![]()
According to Fatou lemma, for arbitrary![]() ,
, ![]() , then almost sure there are only finite
, then almost sure there are only finite ![]() in a finite interval, such that
in a finite interval, such that![]() , this means
, this means![]() .
.
Theorem 3 If![]() , then
, then
(1) Almost sure, ![]() do not contain any interval,
do not contain any interval,
(2) Almost sure, ![]() is a dense set in itself.
is a dense set in itself.
Proof (1) Obviously, ![]() is a optional set, denote
is a optional set, denote ![]() (where we assume
(where we assume![]() ), then
), then ![]() is a monotone increasing left continuous process, and adapt in
is a monotone increasing left continuous process, and adapt in![]() , denote
, denote![]() , thus
, thus ![]() is a optional right continuous process. Let
is a optional right continuous process. Let
![]() ,
,
It is easy to check that![]() , thus
, thus ![]() is a optional set adapt in
is a optional set adapt in![]() .
.
Assume ![]() is debut time, If
is debut time, If![]() , by Section Theorem, exists a stopping time
, by Section Theorem, exists a stopping time ![]() in
in![]() , such that
, such that![]() , and
, and ![]() on
on![]() , by (2) in the theorem 1,
, by (2) in the theorem 1,
![]()
this is a contradictory proposition, thus ![]() and almost sure
and almost sure ![]() do not contain any interval.
do not contain any interval.
(2) The proof is similar to (1).
3. The Significance Probability of Kolmogorov Equations
Theorem 4 For arbitrary![]() ,
, ![]() and
and ![]()
![]() , (1)
, (1)
if and only if![]() .
.
Proof For arbitrary![]() ,
,
![]()
![]()
then (1) and the following equation is equivalence.
![]() (2)
(2)
According to Theorem 1, we have
![]()
and the necessary and sufficient condition of equality is![]() .
.
For arbitrary ![]() let
let ![]() is the first k i-interval of
is the first k i-interval of![]() ,
,
![]()
Corollary 1 The following conditions are equivalence [16] [17] .
(1) The backward equation of Kolmogorov is true,
(2) For arbitrary![]() ,
,
(3) Density matrix ![]() is conservative,
is conservative,
(4) Almost sure, for all ![]() and
and![]() , we have
, we have![]() .
.
Theorem 5 For arbitrary ![]()
![]() (3)
(3)
if and only if for all ![]() -interval
-interval ![]() almost sure
almost sure![]() .
.
Proof (1) Asumme![]() ,
,
![]()
![]()
Obviously ![]() are not intersection. It is easy to check if there are infinite
are not intersection. It is easy to check if there are infinite ![]() to make
to make![]() ,
,
then![]() , and if
, and if![]() , then existing
, then existing![]() , when
, when![]() , we have
, we have![]() , thus that
, thus that![]() , and
, and
![]()
(2) For arbitrary![]() , by (1),
, by (1),
![]() (4)
(4)
and the necessary and sufficient condition of equality is![]() .
.
Thus we get the equation
![]() , (5)
, (5)
let ![]() go to
go to ![]() in Equation (5), we can obtain Equation (3).
in Equation (5), we can obtain Equation (3).
Corollary 2 The Kolmogorov forward equations are true if and only if for all ![]() and i-interval
and i-interval![]() , almost sure
, almost sure![]() .
.
Remark 3 Equation(3) is equivalent to
![]() . (6)
. (6)
Remark 4 If ![]() contains some transient state, then Equation (1) is true if and only if
contains some transient state, then Equation (1) is true if and only if
![]()
Remark 5 Under the condition of![]() , Equation (1) is not probably true. for the example
, Equation (1) is not probably true. for the example
in Remark 1, the Ray-Knight compaction of ![]() under the resolvent
under the resolvent ![]() is
is![]() , thus, the corresponding
, thus, the corresponding
regular chain meets the equation![]() , but according to Corollary 2, Doob process does not
, but according to Corollary 2, Doob process does not
satisfy Kolmogorov forward equation, then ![]() also does not satisfy forward equation.
also does not satisfy forward equation.
If ![]() is an non-honest transition function with total stability, then we can construct a
is an non-honest transition function with total stability, then we can construct a
honest transition function ![]() on
on ![]() such that
such that
![]() , (7)
, (7)
where the density matrix of ![]() is
is ![]() such that
such that
![]() (8)
(8)
the resolvent of ![]() is
is![]() , then
, then
![]() (9)
(9)
Assume ![]() is a regular chain corresponding to
is a regular chain corresponding to![]() . For
. For![]() , by Theorem 1,
, by Theorem 1, ![]() is a absorption state, this is
is a absorption state, this is ![]()
Set![]() , obviously
, obviously ![]() is a killing Markov process, for arbitrary
is a killing Markov process, for arbitrary ![]()
![]() , and
, and![]() , we known the transition function
, we known the transition function
of ![]() is
is![]() .
.
For arbitrary![]() , since
, since ![]() then for arbitrary
then for arbitrary ![]() the following equations are Equivalence.
the following equations are Equivalence.
![]()
It is easy to get:
Proposition 1 Assume ![]() is an non-honest transition function with total stability,
is an non-honest transition function with total stability, ![]() is corresponding Markov process with killing, then
is corresponding Markov process with killing, then ![]() satisfy Kolmogorov backward equation if and only if almost sure for all
satisfy Kolmogorov backward equation if and only if almost sure for all ![]() and
and![]() ,
,![]() .
.
Proposition 2 Assume ![]() is an non-honest transition function with total stability,
is an non-honest transition function with total stability, ![]() is corresponding Markov process with killing, then
is corresponding Markov process with killing, then ![]() satisfy Kolmogorov forward equation if and only if almost sure for all
satisfy Kolmogorov forward equation if and only if almost sure for all ![]() and
and![]() ,
,![]() .
.