On a Max-Type Difference System

Decun Zhang, Xibao Li, Liying Wang, Shiwei Cui

Institute of Systems Science and Mathematics, Naval Aeronautical and Astronautical University, Yantai, China.

DOI: 10.4236/am.2014.519281                

Abstract

In this paper, we show that every well-defined solution of the max-type system of difference equations , , is eventually periodic with period four.

Keywords

Periodic Solution, Max-Type Difference System

1. Introduction

Max-type difference equations and max-type difference systems have been wisely applied in biology, computer science and automatic control systems and so on. There has been great interest in studying these equations in recent years.

For example, Briden et al. [1] investigated the periodicity character of the solution of the max-type difference equation

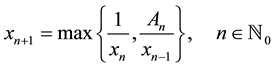
Xiao Qian et al. [2] showed that the solution of the max-type difference equation

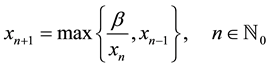
is periodic with period two.

W. Q. Ji et al. [3] showed that the solution of the max-type difference system

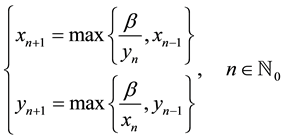
is periodic with period two.

In addition, E. M. Elasyed, Stevo Stević and others investigated some periodic max-type difference equations and periodic max-type difference systems in [4] - [7] .

In this paper we show that every solution of the following max-type difference system

(1)

where the initial conditions 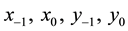are arbitrary non-zero real numbers and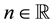, is periodic with period four.

Remark 1. Note that if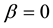, then System (1) becomes, , 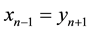from which it follows that, 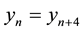and every solution is periodic with period four.

2. Some Lemmas

Lemma 1 Assume that 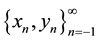is a solution of System (1) and there exists a such that

(2)

Then every solution is periodic with period four.

Proof Frist, we will prove that

(3)

where, from which the lemma follows.

Now, we use the method of induction. For, Equation (3) becomes the following equations

(4)

By System (1) and Equation (2), we obtain that

From which, Equation (4) holds.

Assume Equation (3) holds for, and by using System (1) and Equation (2), we obtain that

So we complete the proof.

Lemma 2 Assume that. Then every solution of System (1) is positive if initial conditions satisfy one of the following conditions or or or.

Proof Without loss of generality, we assume that and from System (1) we have

By using the method of induction, we have

Similarly, when or or, there exists an such that

The proof is completed.

Lemma 3 Assume that. Then every solution of System (1) with positive initial conditions is periodic with period four.

Proof By System (1), we obtain that

Let, , and there are four cases which need to be discussed.

Case 1.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four. Moreover, we have

where, and the solution has the following form

Case 2.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four. Moreover, we have

where, and the solution has the following form

Case 3.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four. Moreover, we have

where, and the solution has the following form

Case 4.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four. Moreover, we have

where, and the solution has the following form

So we complete the proof.

Lemma 4 Assume that. Then every solution of System (1) with negative initial conditions is periodic with period four.

Proof Since and, by induction we have. If we use the change and System (1) can be rewritten as follows

(5)

where.

Now, we will prove that every solution of System (5) with positive initial conditions is periodic with period four.

Let, ,. Similar to the proof of Lemma (3), there are four cases which need to be discussed.

Case 1.. We obtain that

Case 2.. We obtain that

Case 3.. We obtain that

Case 4.. We obtain that

So we complete the proof.

Lemma 5 Assume that. Then every solution of System (1) is periodic with period four if initial conditions satisfy one of the following conditions

Proof If, by using System (1), we know that there is only one case which needs to be discussed. That is

Then we have

Hence,. And by Lemma 1, we have that the solution is periodic with period four.

The proof of case is similar to the proof of case, so we omit it. Then, the proof is completed.

Lemma 6 Assume that. Then every solution of System (1) is periodic with period four if initial conditions satisfy one of the following conditions

Proof If, by using System (1), we know that so there are two cases which need to be discussed. That is

Case 1.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four.

Case 2.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four.

The proof of case is similar to the proof of case, so we omit it. Then, the proof is completed.

Lemma 7 Assume that. Then every solution of System (1) is periodic with period four if initial conditions satisfy one of the following conditions

Proof If, by using System (1), we know that there are four cases which need to be discussed. That is

Case 1.. We have

Hence,. And by Lemma 1, we have that the solution is periodic with period four.

The proof of case is similar to the proof of case in Lemma 3, so we omit it and case is completed.

Similarly, the proof of case is similar to the proof of case, so we omit it.

3. Main Results

By using Lemma 2 and Lemma 3, we obtain the following result.

Theorem 1 Assume that. Then every solution of System (1) is periodic with period four if initial conditions satisfies one of the following conditions or or or.

By using Theorem 1 and Lemma 4, we obtain the following result.

Theorem 2 Assume that. Then every well-defined solution of System (1) is periodic with period four.

By using Lemma 5, Lemma 6 and Lemma 7, we obtain the following result.

Theorem 3 Assume that. Then every well-defined solution of System (1) is periodic with period four.

By using Theorem 2 and Theorem 3, we obtain the following result.

Theorem 4 Assume that. Then every well-defined solution of System (1) is periodic with period four.

Acknowledgements

We thank the Editor and the referee for their comments. Research supported by Distinguished Expert Foundation and Youth Science Foundation of Naval Aeronautical and Astronautical University.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Briden, W.J., Grove, E.A., Kent, C.M. and Ladas, G. (1999) Eventually Periodic Solutions of , Nonlinear Analysis, 6, 31-34.
[2]	Xiao, Q. and Shi, Q.H. (2013) Eventually Periodic Solutions of a Max-Type Equation. Mathematical and Computer Modelling, 57, 992-996. http://dx.doi.org/10.1016/j.mcm.2012.10.010
[3]	Ji, W.Q. (2013) On the Behavior of the Solution of Several Difference Equations and the Difference System. Naval Aeronautical Engineering Institute, Yantai.
[4]	Simsek, D., Cinar, C. and Yalcinkaya, I. (2006) On the Solutions of the Difference Equation . International Journal of Contemporary Mathematical Sciences, 1, 481-487.
[5]	Elsayed, E.M. and Stevic, S. (2009) On the Max-Type Equation . Nonlinear Analysis, 71, 910-922. http://dx.doi.org/10.1016/j.na.2008.11.016
[6]	Stevc, S. (2012) On Some Periodic Systems of Max-Type Difference Equations. Applied Mathematics and Computation, 218, 11483-11487. http://dx.doi.org/10.1016/j.amc.2012.04.077
[7]	Stevic, S. (2012) Solutions of a Max-Type System of Difference Equations. Applied Mathematics and Computation, 218, 9825-9830. http://dx.doi.org/10.1016/j.amc.2012.03.057