Comparison of the Bayesian Methods on Interval-Censored Data for Weibull Distribution ()
1. Introduction
The Weibull distribution observably has the widest variety of applications in many areas, including life testing, reliability theory and others. The most used methods, which are considered to be the traditional methods, are maximum likelihood and the moment estimation (Cohen and Whitten, [1] ). Sinha [2] estimated the parameters of Weibull distribution by maximum likelihood and Bayesian using Lindley’s approximation. Smith [3] developed the maximum likelihood and Bayesian estimators and compared them using the three-parameter Weibull distribution. Singh et al. [4] used the Bayesian estimation approach to estimate the parameters of exponentiated Weibull. Hossain and Zimmer [5] estimated the scale and shape parameters of Weibull distribution using complete and censored samples by maximum likelihood estimator and least squares method. Nassar and Eissa [6] obtained the Bayesian approach using Lindely approximations to estimate the two shape parameters and the reliability function of the exponentiated Weibull distribution. Soliman et al. [7] estimated Weibull distribution by using maximum likelihood estimator and Bayesian approach followed by estimating the hazard and reliability functions. Kantar and Senoglu [8] reported their findings on the comparative study for the location and scale parameters of the Weibull distribution with a given shape parameter. Gupta et al. [9] estimated Weibull extension model by Bayesian method using Markov Chain Monte Carlo (MCMC). Kundu and Howlader [10] obtained Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data, where the Gibbs sampling technique was used to generate MCMC samples from the posterior distribution followed by an importance sampling technique for constructing the Bayes estimation. Comparison between Bayesian and maximum likelihood estimation of the scale parameter in Weibull distribution with known shape was considered by Pandey et al. [11] .
2. Methodology
2.1. Maximum Likelihood Estimation of Weibull Distribution with Interval-Censored Data
The probability density function of Weibull distribution is:
The cumulative distribution function (cdf) of the Weibull distribution is given as
with the scale parameter 
and the shape parameter 
of the Weibull distribution The likelihood function of interval censored as given in Flygare et al. [12] is
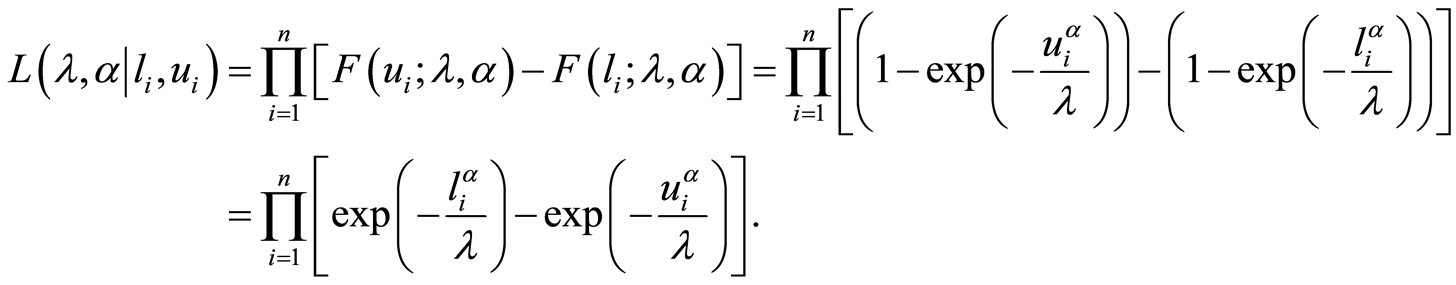(1)
The logarithm of the likelihood function with interval censored can be expressed as follows:
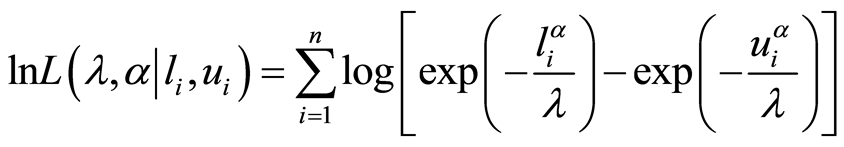(2)
To obtain the equations for the unknown parameters, we differentiate Equation (2) partially with respect to the scale and shape parameters and equal it to zero. The resulting equations are given respectively as,
(3)
(4)
where
cannot be solved analytically, and for that we employed Newton Raphson method to find the numerical solution.
2.2. Bayesian Using Gamma Prior Estimation of Weibull Based on Interval-Censored Data
In this subsection we consider the case when both the scale and shape parameters are unknown, and we compute the Bayes estimates of the shape and scale parameters. It is assumed that 
and 
each have independent gamma
, and gamma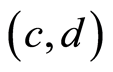 
priors respectively
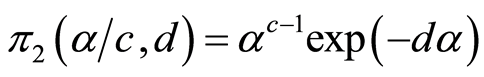
It is a natural conjugate prior.
The posterior probability density function of 
and 
given the data with gamma prior is combining Equation (7) with likelihood function and using Bayes theorem, the joint posterior distribution is derived as see Al Omari et al. [13]
(8)
With this, the Bayes estimates for the scale and shape parameters under squared error loss function are given as:
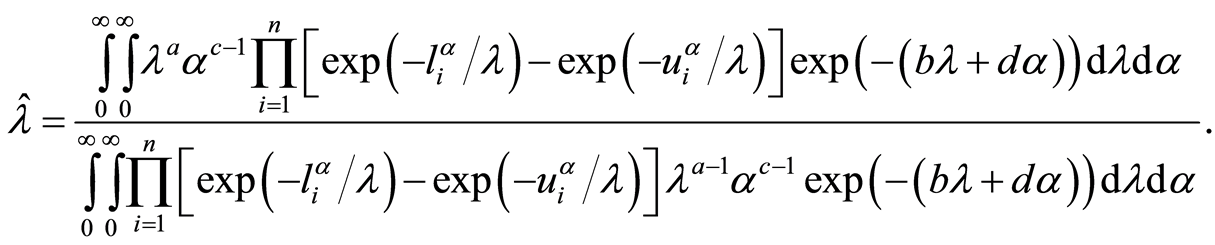(9)
(10)
The integration of the scale and shape parameter we can’t solve it analytical for that we used MetropolisHastings algorithm and Lindley’s approximation to solve the problem.
Metropolis-Hastings Algorithm
The Metropolis-Hastings algorithm is a very general Markov Chain Mote Carlo method, it can be used to obtain random samples from any arbitrarily complicated target distribution of any dimension that is known up to a normalizing constant. In fact, Metropolis algorithm is an alternative to Gibbs sampler that does not require availability of full conditionals see Hastings [14] and Soliman et al. [15] .
Therefore, the full conditional of the posterior density function using gamma prior of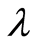 
and 
given the data are combining the gamma prior with likelihood as given below
(11)
From Equation (11) we can get the conditional posterior of the scale parameter 
as follows
(12)
The conditional posterior of the shape parameter 
is given below
(13)
As show in the conditional posterior of the scale and shape parameters it’s not follow any close distribution for that we suggest to use the Metropolis-Hastings algorithm to generate MCMC sample.
Algorithm:
1) Start with initial value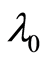
, 
2) The current value
, 
and generate the candidate value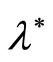
, 
from arbitrary distribution uniform (0, 1).
3) The next value of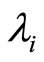 
is given below as
where
4) Generate u from Uniform (0, 1) and accept 
with probability p if 
and return to step 2), otherwise accept
.
5) The next value of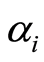 
is given below as
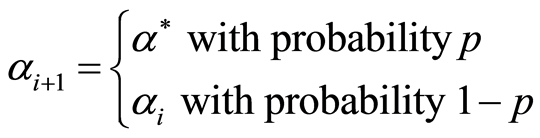
where
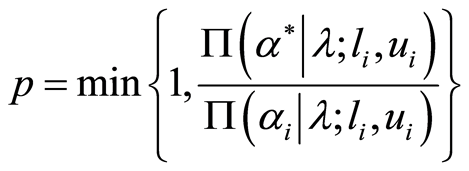
6) Generate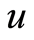 
from uniform (0, 1) and accept 
with probability p if 
and return to step 2), otherwise accept 
and return to step 2).
7) The Bayesian based interval-censored data of the scale and shape parameters under the squared error loss function is given as
8) Obtain the posterior variance of Bayesian using gamma prior based interval-censored data as
2.3. Lindley’s Approximation
The Equations (9) and (10) cannot be solved analytically and for that we obtained Lindley’s expansion to solve the parameters approximation.
According to Al Omari et al. [16] Lindley’s approximation proposed a ratio of integral of the form
where 
is the log-likelihood and
, 
are arbitrary functions of 
in applying this procedure, it is assumed that 
is the prior distribution for 
and 
with 
being some function of interest.
The posterior expectation according to Sinha [2] is
where
According to [1] Lindley expansion is therefore approximated asymptotically by
where L is the log-likelihood equation in (2). See Sinha [2] for more detail.
Taking the scale parameter 
estimation, where
For the shape parameter
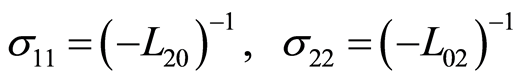
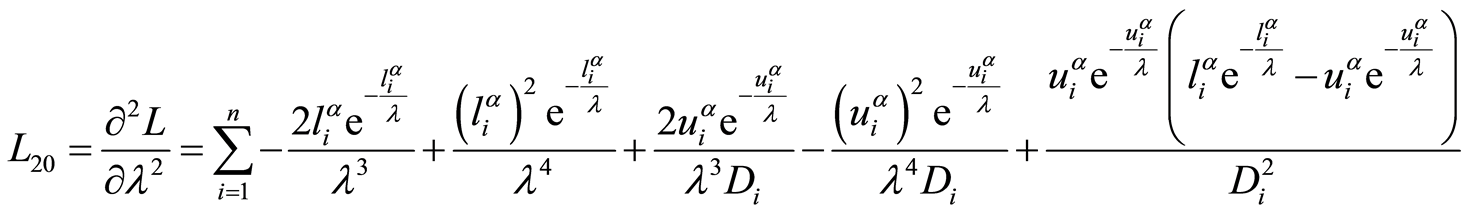
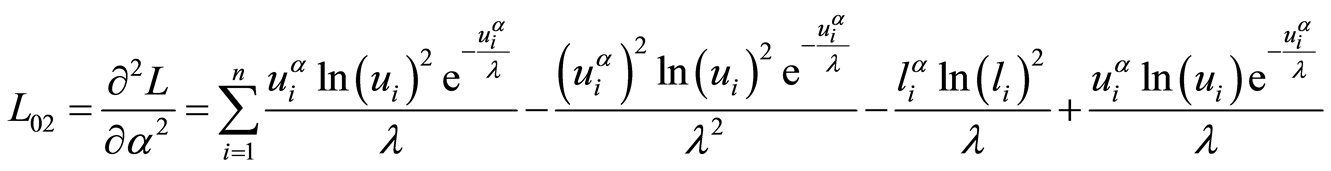
3. Simulation Study
To assess the performance of the maximum likelihood and Bayesian with help of the Lindley’s approximation and Markov Chain Monte Carlo, where the Metropolis-Hastings algorithm used to estimate the scale and shape parameters, the mean squared errors (MSE) for each method were calculated using 10,000 replications for sample size n = 25, 50 and 100 of Weibull distribution with interval-censored data for different value of parameters were the scale parameter
, shape parametric
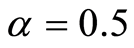, 1, 1.5 and 2, the considered values of
, 
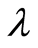are meant for illustration only and other values can also be taken for generating the samples from Weibull distribution.
4. Discussion
As shown in Table 1, the estimate of the scale parameter 
of Weibull distribution with interval-censored data was compared between maximum likelihood (MLE), Bayesian using Lindley’s approximation (BL) and Bayesian using Metropolis-Hastings algorithm (BM) by mean squared error (MSE). We observed that the Bayesian using
Table 1 . Estimated average lengths of the scale parameter and MSE of Weibull distribution.
Table 2. Estimated average lengths of the shape parameter and MSE of Weibull distribution.
Metropolis-Hastings algorithm (BM) is better compare to the others, moreover, Bayesian with help from Lindley’s approximation is better than MLE estimators when
. When the number of sample size increases the mean squared error (MSE) decreases in all cases.
In Table 2, the estimate of the shape parameter 
of Weibull distribution with interval-censored data was compared between maximum likelihood (MLE), Bayesian using Lindley’s approximation (BL) and Bayesian using Metropolis-Hastings algorithm (BM) by mean squared error (MSE). We found that the Bayesian using Metropolis-Hastings algorithm (BM) is the best compare to the others, moreover, Bayesian using Lindley’s approximation is better than MLE estimators when
. When the number of sample size increases the mean squared error (MSE) decreases in all cases.
5. Conclusion
The Bayesian using Metropolis-Hastings algorithm for estimating the scale and shape parameters of Weibull distribution-based interval-censored data is the best compare to others. In this paper, we contribute applying Bayesian estimation approach based on interval-censored data considered with Bayes using Makov Chain Monte Carlo (MCMC).