Volume of Geodesic Balls in Finsler Manifolds of Hyperbolic Type

Carlos Ogouyandjou

Institut de Mathematiques et de Sciences Physiques (IMSP), Universite d’Abomey-Calavi, Porto-Novo, Republic of Benin.

DOI: 10.4236/apm.2014.48050                

Abstract

Let  be a compact Finsler manifold of hyperbolic type, and  be its universal Finslerian covering. In this paper we show that the growth function of the volume of geodesic balls of  is of purely exponential type.

Keywords

Finsler Manifold, Gromov Hyperbolic Manifold, Critical Exponent, Volume Entropy

1. Introduction and Main Results

A Finsler manifold is called of hyperbolic type, if there exists on the manifold M a Riemannian metric 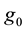of strictly negative curvature such that F and 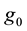are uniformly equivalent (cf. Definition 2.3).

We say that a function 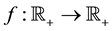is of purely exponential type if there exist constants and 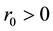such that

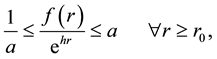
for some constant 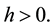The real number h is called the exponential factor of f. In 1969, Margulis (see [1] ) proved, for suitable constan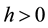t that

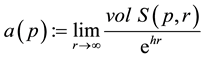
exists at each point p in manifolds of negative curvature and that the function a is continuous.

Clearly, this result implies purely exponential growth of volume of geodesic spheres. In 1979, Manning introduced a notion of volume entropy 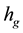of a compact Riemannian manifold 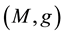as follows (see [2] ): if 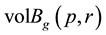denotes the volume of the geodesic ball with centre p and radius r in the universal Riemannian covering X of,

where the limit on the right hand side exists for all and, in fact, is independent of p.

Manning showed that, in the case of non-positive curvature, coincides with the topological entropy.

In 1997, using the notions of Busemann density and Patterson Sullivan measure, G. Knieper proved the following result (see [3] ):

If is a rank-1 compact Riemannian manifold of non-positive curvature and its universal Riemannian covering, there exist constants and such that

Let be a compact Riemannian manifold of hyperbolic type without conjugate points, and X be its universal Riemannian covering. In 2005, we show that the growth function of the volume of geodesic spheres of X is of purely exponential type with the volume entropy as exponential factor (see [4] ).

The main result of this paper is the following:

Theorem 1.1. Let be a compact Finsler manifold of hyperbolic type and be its universal Finslerian covering (cf. Definition 2.3). Let be the volume entropy of F (cf. Definition 2.1). Then, the growth function of the geodesic balls of is of purely exponential type with as exponential factor.

Theorem 1.1 implies the following Corollary:

Corollary 1.2. Let be a compact Finsler manifold of hyperbolic type and be its universal Finslerian covering. Then, the critical exponent (cf. Definition 4.2) of the group of the Deck transformations of is equal to the volume entropy of.

However, from Theorem 1.1, since all compact orientable surfaces of genus greater than one admits a metric of strictly negative curvature, we deduce the following properties:

Corollary 1.3. Let M be a compact orientable surface of genus greater than one, F a Finsler metric on M and be its universal Finslerian covering. Then, the growth function of the geodesic balls of is of purely exponential type with as exponential factor.

The paper is organized as follows: in Section 2, we recall some basic facts about the volume entropy of a compact Finsler manifold. Section 3 is devoted to the ideal boundary and the Gromov boundary of the universal Finslerian covering of a Finsler manifold of hyperbolic type. In Section 4, we introduce a notion of quasi-convex cocompact group and we provide the proof of the Theorem 1.1.

2. The Volume Entropy of a Finsler Manifold of Hyperbolic Type

In this section, we briefly recall some notions from Finsler geometry; see [5] or [6] and the references therein for more details. Let M be a manifold and denote by the natural projection of TM into M. A Finsler structure of M is a function

with the following properties:

1) is on the slit tangent bundle;

2) for all;

3) The Hessian matrix

is positive definite at every point of.

Note that any Riemannian manifold is a Finsler manifold with Let be a

piecewise curve with velocity. Its length. For and

, denote by the collection of all piecewise curves with and. Define the metric distance from p to x by

Note that if F is typically positively homogeneous (of degree 1) the distance is non-symmetric.

We say that the Finsler structure F is absolute homogeneous is

In this case, the distance is symmetric. Let denote by and . Every Finsler manifold comes with a natural volume form, which is described as follows:

Fix an arbitrary Riemannian metric g on M and let be its volume form. Denote by and the units balls of radius 1 with respect to g and F respectively, and let and be their volume with respect to g.

The Finsler form is given by

which is independant of the choice of the Riemannian metric g.

Definition 2.1. Let be a compact Finsler manifold and its universal Finslerian covering. The volume entropy of F is defined by:

Definition 2.2. Let be a Finsler manifold.

1) A piecewise curve satisfying is said to be minimal if .

2) A curve is called a forward ray if is minimal for all.

3) A curve is called a backward ray if is minimal for all.

4) A curve is called a minimal geodesic if is minimal for all.

Definition 2.3. Let be a Finsler manifold M. We say that F is uniformly equivalent to a Riemannian metric g, if there is a constant such that

Let be the universal covering of M. Using the map p, we pull the Finsler structure F back to. The resulting defines on a Finsler structure. We denote by the Finsler manifold. is the universal Finslerian covering of the Finsler manifold

Let be the group of deck transformations. We say that F is invariant under if

Remark 2.4. Note that if M is compact manifold and F is invariant under the deck transformation then F and g are uniform equivalence.

3. Ideal and Gromov Boundaries of Finsler Manifolds of Hyperbolic Type

The following theorem is fundamental for the study of the ideal boundary of Finsler manifolds of hyperbolic type. It was proved by Morse in dimension 2 and by Klingenberg in arbitrary dimensions. The fact that the Morse Lemma also holds in Finsler case was first observed by E. M. Zaustinsky (see [7] ). Due to Klingenberg (see [8] ), the Morse Lemma holds in any dimension.

Theorem 3.1. (Morse Lemma, cf. [9] ) Let be a Finsler manifold of hyperbolic type and g₀ be a metric of strictly negative curvature on M such that F and g₀ are uniformly equivalent and be the universal covering of M. Then there is a constant with the following properties.

1) for any two points x and, the g₀-geodesic-segment from x to y and any F-minimal segment from x to y we have

2) If is a F-forward ray, then there exists a g₀-ray such that

These properties stay hold for F-backward rays and F-minimal geodesics.

Now let be a compact Finsler manifold of hyperbolic type and be its universal Finslerian covering. Let g₀ denote an associated metric of strictly negative curvature on M. Note that the universal Riemannian covering of is a Hadamard manifold and let denote by its ideal boundary. Two F-forward rays c and are said to be asymptotic if there exists a constant such that , where d_H is the Hausdorff distance with respect to the distance d_F. This defines an equivalence relation on the set of F-forward rays of. Let be the coset of asymptotic F-forward rays c of. For each F-forward ray c of, it follows from Morse Lemma that there exists a g₀-geodesic ray such that, where D is the constant in Morse Lemma. Let be the equivalence class of a F-forward ray c and let the equivalence class of the g₀-geodesic. The map f defined by

is bijective. Then f defines on a natural topology with respect to which and are homeomorphic.

Let recall now some basic facts about Gromov hyperbolic spaces. Let be a metric space with a reference point x₀. The Gromov product of the points x and y of X with respect to x₀ is the nonnegative real number defined by:

Let. A metric space is said to be a -hyperbolic space if

for all x, y, z and every choice of reference point x₀. We call X a Gromov hyperbolic space if it is a δ-hyperbolic space for some. The usual hyperbolic space is a δ-hyperbolic space, where. More generally, every Hadamard manifold with sectional curvature for some constant is a δ-hyperbolic space, where (see [10] or [11] ).

Lemma 3.2. (see [11] or [12] ) Let be a complete geodesic δ-hyperbolic space, x₀ a reference point in X, x and y two points of X. Then

for every geodesic segment joining x and y.

Definition 3.3. A function is called k-convex if for all, and,

Proposition 3.4. (see [11] or [12] ) Let be a δ-hyperbolic geodesic space and two minimizing geodesics. The function

is 4δ-convex.

Definition 3.5. Let and be two metric spaces. A map is called a quasi- isometric map, if there exist constants and with:

In a metric space X, a quasi-geodesic (resp. quasi-geodesic ray) is a quasi-isometric map (resp.).

Lemma 3.6. (see [11] ) Let be a metric space and be a geodesic Gromov hyperbolic space. If there exists a quasi-isometric map, then is also a Gromov hyperbolic space.

Now let X be a Gromov hyperbolic manifold, a reference point in X. We say that the sequence of points in X converges at infinity if

If is another reference point in X,

Then the definition of the sequence that converges at infinity does not depend on the choice of the reference point. Let us recall the following equivalence relation on the set of sequences of points in X that converge at infinity:

The Gromov boundary of X is the coset of sequences that converge at infinity.

Let X be a simply connected manifold which is a Gromov hyperbolic space. One defines on the set a topology as follows (see [11] page 22):

1) if, a sequence converges to x with respect to the topology of X.

2) if defines a point converges to

3) For and let

where

for x and y elements of

The set of all and the open metric balls of X generate a topology on With respect to this topology, X is dense in and is compact.

Lemma 3.7. (see [13] ) Let X be a δ-hyperbolic space. Then

1) Each geodesic defines two distinct points at infinity and

2) For each, there exists a geodesic ray such that and For any other geodesic ray with and we have for all

Definition 3.8. Let and be a minimal geodesic ray satisfying The function

is well-defined on X and is called the Busemann function for the geodesic c.

Lemma 3.9. (see [13] ) Let X be a δ-hyperbolic space, and c a geodesic ray with and. Then there exists a neighbourhood of in such that

where is the busemann function for the geodesic c and K is a constant depending only on

Lemma 3.10. (see [11] ) Let be a metric space and be a geodesic Gromov hyperbolic space. If there exists a quasi-isometric map, then is also a Gromov hyperbolic space. Moreover, if the map

is bounded above, i.e. is homeomorphic to

The following lemma give an homeomorphism between the ideal boundary and the Gromov hyperbolic boundary of Hadamard manifolds:

Lemma 3.11. (see [14] ) Let X₀ be a Hadamard manifold with sectional curvature for some constant There exists a natural homeomorphism

In particular,

Using Morse Lemma, (see Lemma 3.11) and the properties of the ideal boundaries, we obtain the following lemma:

Lemma 3.12. Let be a compact Finsler manifold of hyperbolic type and be its universal Finslerian covering. Let g₀ be an associated metric of strictly negative curvature on M and be the universal Riemannian covering of We have

Proof. Since is a Hadamard manifold for some constant, it is a Gromov hyperbolic manifold and (see Lemma 3.11). On the other hand, the fact that F is uniformly equivalent to a Riemannian metric g₀ implies that is also a Gromov hyperbolic space and (see Lemma 3.10). Finally, using the construction of the ideal boundary of, we have. □

4. The Growth Rate of the Volume of Balls in Finsler Manifolds of Hyperbolic Type

Definition 4.1. Let X be a Gromov hyperbolic manifold with reference point and be a discrete and infinite subgroup of the isometry group of. For a given point, the limit set is the set of the accumulation points of the orbit in.

Definition 4.2. Let be a metric space and be a discrete and infinite subgroup of the isometry group of X. For and,

denotes the Poincaré series associated to. The number

is called the critical exponent of and is independent of x and. The subgroup is called of divergence type if the Poincaré series diverge for. The following lemma introduces a useful modification (due to Patterson) of the Poincaré series if is not of divergence type.

Lemma 4.3. (see [15] ) Let be a discrete group with critical exponent. There exists a function which is continuous, nondecreasing and such that

and the modified series

converges for and diverges for.

Let now be a compact Finsler manifold of hyperbolic type, and be its universal Finslerian covering. Let g₀ denote a metric of strictly negative curvature on M. The universal covering of is a Hadamard manifold satisfying for some constant.

Let be the group of deck transformations of and be its critical exponent with respect to the metric. It follows from Theorem 5.1 in [3] that:

The fact that M is compact implies the existence of a constant such that

Then, the critical exponent of with respect to the metric d_F belongs to.

Lemma 4.4. Let be a compact Finsler manifold of hyperbolic type, be its universal Finslerian covering and be the group of deck transformations of. Then

1).

2) for all and.

3) is independent of.

4).

Proof of Lemma 4.4.

1) Direct because and.

2) Let. There exists a sequence such that Then

3) For all, by the definition there is a sequence of points of such that . Then

For all, we have:

Hence,

then.

4) Let g₀ denotes a metric of strictly negative curvature on M. The universal Riemannian covering of

is a Hadamard manifold satisfying for some constant. Then

(see [3] ). Since is cocompact, the identity map defines a homeomorphism

(see Lemma 3.12). Let and such that. The fact

that, there is a sequence in and such that the sequence converges to in. Then concerges to in. □

Let now be a Gromov hyperbolic manifold, and be a non trivial subgroup of and the limit set of the orbit in.

The gromov hull of is the subset of X defined by the collection of the images of the geodesics satisfying and.

Definition 4.5. A non trivial subgroup of the isometry group is quasi-convex cocompact if is compact.

The following lemma is due to Coornaert (see [13] ).

Lemma 4.6. Let be a Gromov hyperbolic manifold with reference point, and be a quasi- convex cocompact subgroup of the isometry group with critical exponent. Then, for all, there is a constant such that:

for all, where

Proof of Theorem 1.1. By Lemma 4.4, we have. Then, the Gromov hull of is equal to. This implies that is a quasi-convex cocompact subgroup of.

For an orbit of in we consider the map defined by:

Let be a fundamental domain of in. We have:

Let now be a fixed point in and put. For all, and, we have:

and for,

Then,

By Lemma 4.6, there is a constant such that:

for all and. Then, there exist constants and such that:

□

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Margulis, M.A. (1969) Applications of Ergotic Theory to the Investigation of Manifolds of Negative Curvature. Functional Analysis and Its Applications, 3, 335-336. http://dx.doi.org/10.1007/BF01076325
[2]	Manning, A. (1979) Topological Entropy for Geodesic Flows. Annals of Mathematics, 110, 567-573. http://dx.doi.org/10.2307/1971239
[3]	Knieper, G. (2002) Hyperbolic Dynamics and Riemannian Geometry. In: Hasselblatt, B. and Katok, A., Eds., Handbook of Dynamical Systems 1A, Elsevier Science, Amsterdam, 453-545.
[4]	Ezin, J.-P. and Ogouyandjou, C. (2005) The Growth Function of the Volume of Geodesic Balls in Riemannian Manifolds of Hyperbolic Type. IMHOTEP, 6, 9-17.
[5]	Bao, D., Chern, S.-S. and Shen, Z. (2000) An Introduction to Riemann-Finsler Geometry. Graduate Texts in Mathematics 200. Communication in Contemporay Math, No. 4, Springer-Verlag, 511-533.
[6]	Shen, Z. (1977) Volume Comparison and Its Applications in Riemann-Finsler Geometry. Advances in Mathematics, 128, 306-328. http://dx.doi.org/10.1006/aima.1997.1630
[7]	Zaustinsky, E.M. (1962) Extremals on Compact E-Surfaces. Transactions of the American Mathematical Society, 102, 433-445.
[8]	Klingenberg, W. (1971) Geodatischer Fluss auf Mannigfaltigkeiten vom hyperbolishen Typ. Inventiones Mathematicae, 14, 63-82. http://dx.doi.org/10.1007/BF01418743
[9]	Schroder, J.P. (2014) Minimal Rays on Surfaces of Genus Greater than One. arXiv:1404.0573v1 [math.DS]
[10]	Ancona, A. (1988) Théorie du potentiel sur les graphes et les varieties. In: Ancona, A., et al., Eds., Potential Theory, Surveys and Problems, Lecture Notes in Mathematics, No. 1344, Springer-Verlag, Berlin.
[11]	Coornaert, M., Delzant, T. and Papadopoulos, A. (1990) Géométrie et théorie des groups. Lecture Notes in Mathematics. No. 1441, Springer-Verlag, Berlin.
[12]	Coornert, M. and Papadoupoulos, A. (1993) Symbolic Dynamics and Hyperbolic Groups. Lecture Notes in Mathematics, No. 1539, Springer-Verlag, Berlin.
[13]	Coornaert, M. (1993) Mesures de Patterson-Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific Journal of Mathematics, 159, 241-270. http://dx.doi.org/10.2140/pjm.1993.159.241
[14]	Cao, J. (2000) Cheeger Isoperimetric Constants of Gromov Hyperbolic Spaces with Quasi-Pole. Communications in Contemporary Mathematics, 2, 511-533. http://dx.doi.org/10.1142/S0219199700000232
[15]	Patterson, S. (1976) The Limit Set of Fuchsian Group. Acta Mathematica, 163, 241-273. http://dx.doi.org/10.1007/BF02392046