1. Introduction
We consider simple graphs, which have neither loops nor multiple edges. For a graph , let
, let  and
and  denote the set of vertices and the set of edges of
denote the set of vertices and the set of edges of , respectively. We write
, respectively. We write 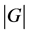 for the order of
for the order of  (i.e.,
(i.e., ). For a vertex
). For a vertex  of
of , the degree of
, the degree of  in
in  is denoted by
is denoted by , and the set of vertices adjacent to
, and the set of vertices adjacent to  is called the neighborhood of
is called the neighborhood of 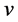 and denoted by
and denoted by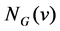 . In particular,
. In particular,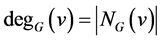 . An edge joining two vertices
. An edge joining two vertices  and
and  is denoted by
is denoted by  or
or .
.
Let 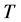 be a tree. A vertex of
be a tree. A vertex of  with degree one is often called a leaf of
with degree one is often called a leaf of , and the set of leaves of
, and the set of leaves of  is denoted by
is denoted by . The subtree
. The subtree  of
of  is called the stem of
is called the stem of  and denoted by
and denoted by . A spanning tree with specified stem was first considered in [1] .
. A spanning tree with specified stem was first considered in [1] .
A tree having at most  leaves is called a k-ended tree. So a tree whose stem has at most
leaves is called a k-ended tree. So a tree whose stem has at most  leaves in it is called a tree with k-ended stem. Notice that a tree with 2-ended stem is nothing but a caterpillar, whose stem is a path. We consider a spanning tree with k-ended stem.
leaves in it is called a tree with k-ended stem. Notice that a tree with 2-ended stem is nothing but a caterpillar, whose stem is a path. We consider a spanning tree with k-ended stem.
We make a remark about spanning trees with k-ended stem from the point of view of dominating set. A subgraph  of a graph
of a graph  is said to dominate
is said to dominate  if every vertex of
if every vertex of  not contained in
not contained in  has a neighbor in
has a neighbor in . Namely,
. Namely,  dominates
dominates  if every vertex
if every vertex  satisfies
satisfies . So a graph
. So a graph  has a spanning tree with k-ended stem if and only if
has a spanning tree with k-ended stem if and only if 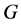 has a k-ended tree that dominates
has a k-ended tree that dominates . There are many researches on dominating cycles and dominating paths (for example, see [2] and [3] with stronger definition of domination). Thus the concept of spanning trees with k-ended stem can be also considered as a generalization of dominating paths.
. There are many researches on dominating cycles and dominating paths (for example, see [2] and [3] with stronger definition of domination). Thus the concept of spanning trees with k-ended stem can be also considered as a generalization of dominating paths.
For an integer  and a graph
and a graph ,
,  denotes the minimum degree sum of
denotes the minimum degree sum of  independent vertices of
independent vertices of . The following theorem gives a sufficient condition using
. The following theorem gives a sufficient condition using  for a graph to have a spanning tree with k-ended stem.
for a graph to have a spanning tree with k-ended stem.
Theorem 1 (Tsugaki and Zhang [4] ) Let  be a connected graph and
be a connected graph and  be an integer. If
be an integer. If

then  has a spanning tree with k-ended stem.
has a spanning tree with k-ended stem.
Another result on spanning trees with k-ended stem is the following.
Theorem 2 (Kano and Yan [5] ) Let  be a connected graph and
be a connected graph and  be an integer. If
be an integer. If  satisfies one of the following conditions, then
satisfies one of the following conditions, then  has a spanning tree with k-ended stem.
has a spanning tree with k-ended stem.
(1) 
(2)  is claw-free and
is claw-free and .
.
A closure operation is useful in the study of the existence of hamiltonian cycles, hamiltonian paths and other spanning subgraphs in graphs. It was first introduced by Bondy and Chvátal.
Theorem 3 (Bondy and Chval [6] ) Let  be a graph and let
be a graph and let  and
and  be two nonadjacent vertices of
be two nonadjacent vertices of .
.
(1) Suppose . Then
. Then  has a hamiltonian cycle if and only if
has a hamiltonian cycle if and only if  has a hamiltonian cycle.
has a hamiltonian cycle.
(2) Suppose . Then
. Then  has a hamiltonian path if and only if
has a hamiltonian path if and only if  has a hamiltonian path.
has a hamiltonian path.
After [6] , many researchers have defined other closure concepts for various graph properties. The following theorem gives a result on closure for spanning k-ended tree.
Theorem 4 (Broersma and Tuinstra [7] ) Let  be an integer, and let G be a graph. Let
be an integer, and let G be a graph. Let 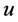 and
and  be a pair of nonadjacent vertices of
be a pair of nonadjacent vertices of  with
with . Then
. Then  has a spanning k-ended tree if and only if
has a spanning k-ended tree if and only if  has a spanning
has a spanning  -ended tree.
-ended tree.
Another type of closure theorem on spanning k-ended tree can be found in Fujisawa, Saito and Schiermeyer [8] . The interested reader is referred to the survey [9] on closure concepts.
In this paper, we prove the following theorem.
Theorem 5 Let  be a connected graph and
be a connected graph and  be an integer. Let
be an integer. Let  and
and  be a pair of nonadjacent vertices of
be a pair of nonadjacent vertices of  such that
such that
 (1)
(1)
Then  has a spanning tree with k-ended stem if and only if
has a spanning tree with k-ended stem if and only if  has a spanning tree with k-ended stem.
has a spanning tree with k-ended stem.
Before proving Theorem 5, we show that the condition (1) in Theorem 5 is sharp. We construct a graph  as follows. Let
as follows. Let  and
and  be integers, and let
be integers, and let  be a complete graph of order
be a complete graph of order , which is a subgraph of
, which is a subgraph of . Let
. Let  be
be  vertices of
vertices of  not contained in
not contained in . Join
. Join 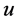 and
and  to all the vertices of
to all the vertices of  by edges. Join
by edges. Join 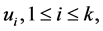 to
to  and
and  by edges. Then the resulting graph is
by edges. Then the resulting graph is  (see Figure 1). It is immediate that
(see Figure 1). It is immediate that  has a spanning tree with k-ended stem, where all the vertices of
has a spanning tree with k-ended stem, where all the vertices of  and
and  are leaves of the spanning tree, and
are leaves of the spanning tree, and . However
. However  has no spanning tree with k-ended stem. Therefore the condition (1) is sharp. Moreover, in Figure 1,
has no spanning tree with k-ended stem. Therefore the condition (1) is sharp. Moreover, in Figure 1,  . Since
. Since  be an arbitrary integer, the degree sum of
be an arbitrary integer, the degree sum of  and
and  can be arbitrarily great. This implies that we can not find a condition similar to Theorem 4 for spanning tree with k-ended stem.
can be arbitrarily great. This implies that we can not find a condition similar to Theorem 4 for spanning tree with k-ended stem.
Some results on spanning k-ended trees and other spanning trees with given properties can be found in [10] , and many current results on spanning trees can be found in [11] .

Figure 1. A graph G having no spanning tree with k-ended stem.
2. Proof of Theorem 5
In this section we prove Theorem 5. Without mentioning, we often use the fact that  is a disjoint union of
is a disjoint union of  and
and .
.
Proof of Theorem 5. Since the necessity of the theorem is trivial, we only prove the sufficiency. Assume, to the contrary, that  has a spanning tree with k-ended stem but
has a spanning tree with k-ended stem but 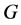 does not have a spanning tree with kended stem. Let us denote
does not have a spanning tree with kended stem. Let us denote . Choose a spanning tree
. Choose a spanning tree  with k-ended stem of
with k-ended stem of  so that
so that
(T1)  is as small as possible, and
is as small as possible, and
(T2)  is as small as possible subject to (T1).
is as small as possible subject to (T1).
It is obvious that the edge  is contained in
is contained in  since otherwise
since otherwise  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of . Let
. Let . Then obviously
. Then obviously .
.
Claim 1. (1) 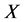 is an independent set of
is an independent set of ; (2) For every
; (2) For every , there exists a vertex
, there exists a vertex  that is adjacent to
that is adjacent to  in
in  and
and .
.
By the choice (T1), it is easy to see that if , then
, then  is an independent set of
is an independent set of , and so is of
, and so is of . Assume that
. Assume that  and the two leaves
and the two leaves  and
and  of
of  are adjacent in
are adjacent in . It is easy to see that
. It is easy to see that  and
and  are not adjacent in
are not adjacent in  since otherwise we can obtain a spanning tree with 2-ended stem of
since otherwise we can obtain a spanning tree with 2-ended stem of  from
from . If
. If  and
and  are both contained in
are both contained in , then
, then 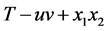 is a spanning tree with 2-ended stem of
is a spanning tree with 2-ended stem of , which contradicts the assumption. Hence we may assume that
, which contradicts the assumption. Hence we may assume that  is a vertex of
is a vertex of  and
and  is a leaf of
is a leaf of  by symmetry of
by symmetry of 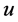 and
and  and by
and by . Since
. Since  is connected,
is connected,  is adjacent to a vertex
is adjacent to a vertex . If
. If  is contained in
is contained in , then
, then  is a spanning tree with 2-ended stem of
is a spanning tree with 2-ended stem of , a contradiction. If
, a contradiction. If  is a leaf of
is a leaf of , let
, let  be the vertex of
be the vertex of  adjacent to
adjacent to  in
in , and let
, and let  be a vertex of
be a vertex of  adjacent to
adjacent to . Then
. Then  is a spanning tree with 2-ended stem of
is a spanning tree with 2-ended stem of , a contradiction. Therefore,
, a contradiction. Therefore,  is an independent set of
is an independent set of . Hence (1) of Claim 1 follows.
. Hence (1) of Claim 1 follows.
Suppose that there exists a vertex ,
,  , such that every leaf
, such that every leaf  adjacent to
adjacent to  in
in  satisfies
satisfies . Then for every leaf
. Then for every leaf  adjacent to
adjacent to 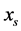 in
in , remove the edge
, remove the edge  from
from 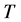 and add an edge
and add an edge  of
of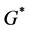 , where
, where . Denote the resulting tree of
. Denote the resulting tree of  by
by .
.
Then  is a spanning tree of
is a spanning tree of  and satisfies
and satisfies , which contradicts the condition
, which contradicts the condition
(T2). Therefore, (2) of Claim 1 holds.
Hereafter, we take the vertices  as in Claim 1(2). Let
as in Claim 1(2). Let . Since the edge
. Since the edge  is contained in
is contained in , let
, let , where
, where  and
and . Since
. Since  is a connected graph, there exist a vertex
is a connected graph, there exist a vertex  and a vertex
and a vertex  which are adjacent in
which are adjacent in .
.
Claim 2.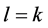 .
.
The claim holds when , and so we assume that
, and so we assume that . If
. If , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which contradicts the assumption. Next we consider the case where
, which contradicts the assumption. Next we consider the case where . If either
. If either  is a leaf of
is a leaf of  or the degree of
or the degree of  in
in  is 1 or greater than 2, then
is 1 or greater than 2, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which contradicts the assumption. Thus the degree of
, which contradicts the assumption. Thus the degree of  in
in  is 2. By symmetry of
is 2. By symmetry of 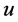 and
and , we may assume that the degree of
, we may assume that the degree of 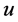 in
in  is also 2, and it is clear that
is also 2, and it is clear that  is an edge of
is an edge of .
.
First we consider  and
and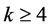 . If a vertex
. If a vertex  is adjacent to
is adjacent to 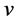 in
in , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , a contradiction. Thus no vertex of
, a contradiction. Thus no vertex of  is adjacent to
is adjacent to  in
in . By symmetry of
. By symmetry of  and
and , no vertex of
, no vertex of  is adjacent to
is adjacent to  in
in . Assume that a vertex
. Assume that a vertex  is adjacent to
is adjacent to  in
in  and
and  contains at least two vertices of
contains at least two vertices of . Then the path in
. Then the path in 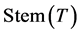 connecting
connecting  and
and  contains a vertex of degree at least 3 in
contains a vertex of degree at least 3 in . Let
. Let 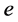 be an edge of the path which is incident with a vertex with degree at least 3 in
be an edge of the path which is incident with a vertex with degree at least 3 in . Then
. Then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , and
, and  has degree at least 3 in
has degree at least 3 in . Then we can derive a contradiction by the same argument as in the above first paragraph. Therefore if a vertex
. Then we can derive a contradiction by the same argument as in the above first paragraph. Therefore if a vertex  of
of 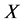 is adjacent to
is adjacent to  in
in , then
, then  contains exactly one vertex of
contains exactly one vertex of . Note that
. Note that  may be adjacent to
may be adjacent to  but not to
but not to . Since
. Since  by
by ,
,  contains at least two vertices of
contains at least two vertices of , which means no vertex of
, which means no vertex of  is adjacent to
is adjacent to  in
in  by the same argument on
by the same argument on  and
and  given above.
given above.
By the above fact and Claim (1), we obtain

which implies  by
by  and
and , which contradicts (1).
, which contradicts (1).
Next we consider the case where  and
and . In this case,
. In this case,  is a path, and let
is a path, and let  and
and  be the leaves of
be the leaves of  where
where  and
and . By the same argument as in the above paragraph, we have that neither
. By the same argument as in the above paragraph, we have that neither  and
and 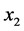 nor
nor 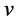 and
and  are adjacent in
are adjacent in . We shall show that
. We shall show that  and
and  are not adjacent in
are not adjacent in . Assume that
. Assume that  and
and  are adjacent in
are adjacent in . Let
. Let  be the vertex adjacent to
be the vertex adjacent to  in
in  if
if  or
or  if
if , and let
, and let  be a vertex adjacent to
be a vertex adjacent to  in
in . Then
. Then  is a spanning tree with 3-ended stem of
is a spanning tree with 3-ended stem of , a contradiction. Similarly,
, a contradiction. Similarly,  and
and  are not adjacent in
are not adjacent in .
.
By the above fact and Claim 1, we obtain

which implies  by
by , which contradicts (1). Hence Claim 2 holds.
, which contradicts (1). Hence Claim 2 holds.
We consider the following two cases:
Case 1.  and
and  are both contained in
are both contained in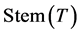 .
.
Subcase 1.1 Both  are
are  are vertices of
are vertices of .
.
In this case, by Claim 1 (2), we have

then  by Claim 2, which contradicts (1).
by Claim 2, which contradicts (1).
Subcase 1.2  is a leaf of
is a leaf of  and
and  is a vertex of
is a vertex of .
.
In this case, without loss of generality, let . If either
. If either  has degree greater than 2 in
has degree greater than 2 in  or
or , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which is a contradiction. Hence
, which is a contradiction. Hence  has degree 2 in
has degree 2 in  and
and .
.
Let  be the vertex adjacent to
be the vertex adjacent to  in
in 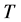 if
if 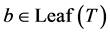 or
or  if
if . Then
. Then  , since otherwise,
, since otherwise,  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of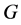 . Let
. Let  be the path connecting
be the path connecting  and
and  in
in . Then there exists at least one vertex
. Then there exists at least one vertex 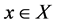 such that
such that  pass through
pass through . We assign an orientation in
. We assign an orientation in  from
from 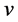 to
to , and
, and  be the successor of
be the successor of . If
. If  and
and  are adjacent in
are adjacent in , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which contradicts the assumption. Therefore, by Claim 1(2), we have
, which contradicts the assumption. Therefore, by Claim 1(2), we have

Then , which contradicts (1).
, which contradicts (1).
Case 2. 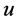 is a vertex of
is a vertex of  and
and 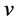 is a leaf of
is a leaf of .
.
Subcase 2.1  is a leaf of
is a leaf of .
.
In this case, if  is adjacent to a vertex
is adjacent to a vertex  in
in , where
, where  is a vertex of
is a vertex of , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which contradicts the assumption. So the neighborhood of
, which contradicts the assumption. So the neighborhood of  is contained in
is contained in . Without loss of generality, let
. Without loss of generality, let  and
and .
.
By Claim 1 (2), we have

Hence
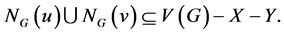
That means , which contradicts (1).
, which contradicts (1).
Subcase 2.2  is a vertex of
is a vertex of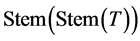 .
.
In this case, by Claim 1 (2), . If there exists some
. If there exists some 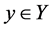 such that
such that , then
, then  is a spanning tree with k-ended stem of
is a spanning tree with k-ended stem of , which contradicts the assumption. Hence
, which contradicts the assumption. Hence . We have
. We have

then , which contradicts (1).
, which contradicts (1).
Consequently, the proof is complete. ,
Acknowledgments
The author would like to thank Prof. Mikio Kano for introducing me to problems on spanning trees with specified stems and for his valuable suggestions.