1. Introduction
In the papers [1] [2] published recently, the new approaches to the measurement of total alkalinity (TAL) and carbonate alkalinity (CAM) were presented. In particular, CAM refers to titrimetric analysis of two systems (V0 mL): NaHCO3 (C01) + Na2CO3 (C02) (System I), and Na2CO3 (C02) + NaOH (Cb) (System II). The results {(Vj, pHj)│j = 1, …, N} obtained from pH titration of the corresponding systems with C mol/L HCl, undertaken under isothermal conditions, are presented according to a modified Gran II method. The CAM concept is fully compatible with the TAL concept, in which other species with acid-base properties are also included.
The equivalence volumes Veqi (i = 1, 2, 3) referring to the corresponding components in Systems I and II are involved in the following relationships:
(1)
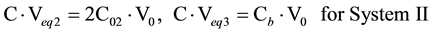(2)
Subsequently, the carbonate alkalinities (CAM, mmol/L) are calculated from the formulae: CAM(I) = 103∙(C01 + 2C02) or CAM(II) = 103∙(2C02 + Cb), i.e.,
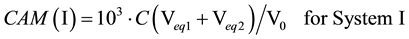(3)
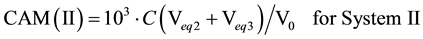(4)
The present paper provides a new approach to the problem in question. This approach enables equivalence volumes (Veqi) to be calculated and the following physicochemical data to be evaluated: dissociation constants (K1 and K2) of H2CO3, the ionic product of water (KW), and the activity coefficient (γ) of hydrogen ions―not only in aqueous media, but also in binary-solvent systems [3] . The functions derived for this purpose have a form similar to those ascribed to Gran II method. The validity of the models proposed was confirmed experimentally by pH titration of synthetic samples referring to Systems I and II.
2. The Gran-type Functions
The Gran functions applicable for determination of CAM(I) (Equation (3)) and CAM(II) (Equation (4)) are detailed in Table 1 [2] . The notations applied there are as follows: ph = −logh, h = γ・[H+] - activity, and γ - the activity coefficient of hydrogen ions;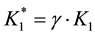
, 
, 
- hybrid values for K1 = [H+][
]/[H2CO3], K2 = [H+][
]/[
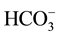], and KW = [H+][OH−]. The pH intervals, in which the corresponding Gran-like functions are valid, are denoted by b, c, d for System I, and by a, b, c, d for System II.
Interval a is not included in System I in Table 1; simply because the data {(Vj, pHj) | j = 1, …, N} do not cover this pH range in System I. Regarding System II, the experimental points may not cover interval a at lower Cb values.
The case where V0 mL of C02 mol/L Na2CO3 is titrated with V mL of C mol/L HCl is a particular case of System I (at C01 = 0) or System II (at Cb = 0). Note that the formulae related to Systems I and II are identical in pH intervals d and c (see Table 1), but the formulae are different in interval b. However, at Vb = Veq1 = 0 and Va = Veq3 = 0, both formulae are simplified into the following form:
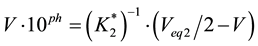(5)
In the data handling step referring to simulated or experimental data {(Vj, pHj) | j = 1, …, N}, the Gran functions are applied to the sequences of pH intervals, such as those specified in Table 1. The use of other possible sequences is not advised.
The parameters:
・ Veq1, Veq2, K1*, K2* and γ (and then K1 = K1*/γ, K2 = K2*/γ) for the modified Gran functions referring to System I, or
・ Veq2, Veq3, K1*, K2* and γ (and then K1 = K1*/γ, K2 = K2*/γ) for the modified Gran functions referring to System II,
can be found according to the least squares method (LSM) [4] [5] applied to the experimental points:
referring separately to particular x intervals: x = b, c, d (System I), or x = a, b, c, d (System II) in Table 1, with the set of Nx points, related to the x-th pH interval. It is worth noting that the ph, referring to activity h of H+ ions, is measured in experimental titrations. The ph = −logh as variable (not pH = −log[H+]) is involved in all relationships specified in Table 1.
3. Calculation Procedure
The functions in Table 1 can be presented in a unified form of the linear regression equation:
![]()
Table 1. The Gran functions related to Systems I and II.
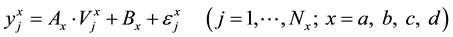(6)
Subsequently, applying LSM to the sum of squares
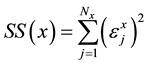(7)
where j refers to the points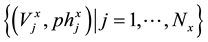 
related to x-th subset (x = a, b, c, d), we obtain the formu-
lae:
![]()
, (8)
where the sum ![]()
covers the points taken from the x-th interval, ![]()
is the j-th V-value taken from the x-th
interval.
As stated above, calculation of the parameters is possible in a defined sequence of operations. For example, the sequence d → c applied in Table 1 for System I means that Vd value, obtained according to LSM for the
data ![]()
composing the subset of the points taken from interval d (Figure 1), is inserted
on the left side of the relationship referring to interval c and LSM is applied to the data
![]()
taken from interval c; in this way, the Vc value is obtained. From Vd and Vc, one can
calculate:
![]()
and ![]()
for System I (Table 1) (9)
![]()
and ![]()
for System II (Table 1) (10)
Moreover, we obtain:
![]()
, ![]()
, ![]()
for Systems I and II (Table 1) (11)
From Table 1, System I, no. b, for the point ![]()
we get
![]()
(12)
where Veq1 and Veq2 are expressed by Equation (1). Similarly, from Table 1, System II, no. b and a, we get
![]()
(13)
![]()
(14)
respectively, where Veq2 and Veq3 are expressed by Equation (2). On the basis of Equation (5), we obtain the relationship:
![]()
(15)
We then calculate:
![]()
and (16)
![]()
and (17)
and
![]()
(18)
where γ is defined in Equation (11). The nearly constant ionic strength value, required during the titration, can be secured by the addition of a basal electrolyte on the stage of D and T preparation.
As revealed from Equations (3), (4), it is necessary to know the sum of equivalence volumes: Veq1 + Veq2 or Veq2 + Veq3, to calculate CAM(I) or CAM(II) value. However, determination of Veqi values (i = 1, 2 or 2, 3) from a single pH titration curve is also possible.
4. Experimental part
4.1. Apparatus and Solutions
The pH titrations were carried out in a 30 mL thermostated, self-made measuring cell, equipped with magnetic stirrer and PT 1000 temperature sensor. The pH measurements and titrations were taken at 22˚C with a Cerko Lab System microtitrator, equipped with 5 mL syringe pump, 3-way valve, and pH electrode (Hydromet, type ERH-13-6). The electrode was standardized with aqueous standard buffers of pH 5.00, 7.00 and 10.00, purchased from the Chempur Company. When not in use, the electrode was stored in 3 mol/L KCl solution. Titrant was added into V0 = 4.00 mL of D stepwise, in aliquots of 0.01 mL, with 6-8-sec. pauses, and the experimental
points ![]()
were recorded.
The reagents: HCl, Na2CO3, NaHCO3, NaOH of p.a. grade, purchased from Chempur Company, were used for the preparation of stock and diluted solutions in doubly distilled (freshly prepared, with conductivity of approx. 0.18 μS/cm) water. Stock solution of hydrochloric acid (HCl) as T, was standardized against Na2CO3, obtained after prior calcination (220˚C, 5 hrs) of commercial disodium carbonate. The NaOH solution was standardized against potassium hydrogen phthalate (p.a., from Merck). Methanol (p.a. grade, 99.5%, supplied by POCH S.A.) was applied for titrations made in binary-solvent media.
Stock titrands were prepared by dilution of weighed portions of Na2CO3 and NaHCO3 in water, or by addition of a weighed portion of Na2CO3 into a standardized NaOH solution. In other titrations, mixed solvent was prepared from appropriate volumes of water and CH3OH, and cooled before preparation of HCl and Na2CO3 solutions. The HCl solution (10% v/v CH3OH) was standardized as described previously. Concentrations of HCl, NaHCO3, Na2CO3 and NaOH in the corresponding solutions are specified below.
4.2. Results and Discussion
The approach was applied first to the results of titrations of Systems I and II, with HCl solution as the titrant, T. Titration in System I was carried out at pre-assumed values (V0, C01, C02, C) = (4.000, 0.01012, 0.02011, 0.10078); Veq1 = 0.01012・4/0.10078 = 0.4017; Veq2 = 2・0.02011・4/0.10078 = 1.5963. The results of exemplary titration are graphically presented in Figure 1. The data obtained for Vd = 2.0122, Vc = 0.8017 (Figure 1(a), Figure 1(b)) are in good agreement with the expected values: 1.9980 and 0.7982 (see Table 2). Moreover, we get here: γ = 0.9283 and ![]()
= 6.379. The pK2j* values, calculated on the basis of Equation (13), are plotted in Figure 1(c), Figure 1(d), with V and ph as the variables on the abscissa, respectively. Some discrepancies in Veq1 value can result from the poor knowledge of NaHCO3 concentration, which is not a primary standard.
Titration in System II was carried out at pre-assumed values (V0, C02, Cb, C) = (4.000, 0.0200, 0.0209, 0.10078). The results obtained from repeated titrations are detailed in Table 3; 2・0.0200・4/0.10078 = 1.5876 and 0.0209・4/0.10078 = 0.08295 are the expected values for Veq2 and Veq3, respectively. Exemplary data are plotted in Figure 2. As can be seen, the sum Vd = Veq2 + Veq3 is very well reproducible in repeated titrations and is in good agreement with the expected value of 2.4171 (Figure 2(a)). The values for Veq2 are slightly smaller than 1.5876, while the values for Veq3 are slightly greater than 0.08295. The repeatability of values for γ and ![]()
is lower. The ![]()
(Figure 2(c)) and ![]()
(Figure 2(d)) values vary regularly (not stochastically) from point-to-point, although the range of ph values covered by the points close to ph ≈ pK2 = 10.1 is narrow (but in a wider pK range than in Figure 1(c), Figure 1(d)); also ![]()
(and pK1 = ![]()
+ logγ values are close to 6.3). The ![]()
values are distinctly higher than 14.0; this may be ascribed to the non-linear characteristics of the glass electrode in alkaline media. Smaller ![]()
values at lower ph support this opinion.
Another option for System II is also possible a priori and starts from equation a in Table 1 (System II) and
finds Va (=Veq3) and ![]()
on the basis of the points![]()
. The Va value is then inserted in
equation b in Table 1 (System II) and Vb (=Veq2/2 + Veq3) and ![]()
values are determined on the basis of the
points![]()
. The Veq2 (= 2(Vb − Va)) and Veq3 values can be compared with those obtained
on the basis of the experimental points in intervals d and c. This procedure could be regarded as a kind of internal validation of the results. However, it should be borne in mind that the results of ph measurements obtained in alkaline media could be loaded by systematic error resulting from the alkaline error of the glass electrode. The errors involved with ph measurements in the a range affect the Va value, subsequently applied in the (V − Va)・10ph vs. V relationship related to interval b; an improper Va value causes this relationship to be a nonlinear one. Therefore, it is advisable to use the experimental points from interval b (for System I) or from intervals a and b (for System II) only for the determination of the related equilibrium parameters, see Equations (12)-(18).
On the basis of known values for Vd found in interval d for Systems I and II (see Table 1), the alkalinities: CAM(I) (Equation (3)), and CAM(II) (Equation (4)) can be calculated; obtaining:
CAM(I) = 0.10078・2.0122/4 = 0.0507 (from Table 2, no. 1),
CAM(II) = 0.10078・2.4123/4 = 0.0608 (from Table 3, no. 3).
5. Final comments
This article provides the new consistent formulation for alkalinities referring to NaHCO3 + Na2CO3 (System I) and Na2CO3 + NaOH (System II) solutions, titrated with HCl. The related formulae, specified in Table 2, are valid in defined pH intervals, denoted as b, c, d or a, b, c, d. The approach based on these new formulae has been called “carbonate alkalinity in a modified version” (CAM). All the formulae are closely relevant to the recently formulated total alkalinity (TAL) [1] [2] . The formulae for CAM are valid within defined pH ranges, in which the relationships between variables are expressed by the functions specified in Table 1.
The CAM approach enables equivalence volumes to be calculated, as well as the following physicochemical data: the activity coefficient (γ) of hydrogen ions; the hybrid values for dissociation constants:![]()
, ![]()
for H2CO3, and ![]()
for the ionic product of water. One of the main novelties of the method is the possibility of determining γ. Moreover, the common equilibrium constants: K1, K2 and KW are also calculated. The possibility of calculating γ is also inherent in the TAL method [1] [2] . Another interesting option is the determination of the related parameters in binary solvent media [6] .
The pH-intervals assumed for calculation of the analytical and physicochemical data are confined (see [2] , p. 229) in comparison with the ones pre-assumed with use of the D = 1.9 value. The narrowing of the pH-range taken for calculations results from the scale of (C01, C02, C) or (C02, C03, C) values applied in the experiments.
The procedure applied here can also be extended to salts other than carbonates. To extend the pH range covered by pH titration, it is suggested that the option involving the addition of a pre-dose is used [2] . When weak acid is considered, the strong base solution can be used as titrant or, after addition of the base as the pre-dose, the mixture can be titrated with a strong acid, as above.
The CAM method was tested experimentally. The results for the dissociation constants of H2CO3 are close to those found in literature [7] . The values for γ are more scattered.
This article attempts to provide an introductory step for further studies about the determination of alkalinity
![]()
Table 2. Results obtained from repeated titrations made in System I.
![]()
Table 3. Results obtained from repeated titrations made in System II.
according to the proposed TAL method [1] [2] for examination of natural, municipal and industrial waters, carbonated soft drinks and wines, as well as different biological systems.
The CAM presented here completes the list of modifications of the Gran methods presented in previously published articles [8] - [12] , referring to different areas of titrimetric analysis.
Symbols used
CAM―carbonate alkalinity [mmol/L] in modified version;
D―titrand (solution titrated);
γ = h/[H+]―activity coefficient for H+ ions;
h―activity of H+ ions;
LSM―least squares method;
pH = −log[H+];
ph = −logh;
T―titrant;
TAL―total alkalinity;
V―volume [mL] of T;
V0―volume [mL] of D;
Veqi―volume [mL] of titrant, referring to the equivalence point (Veqi, pHeqi);
[X]―concentration [mol/L] of the species X.
NOTES
*Corresponding author.