Generalized Inversions of Hadamard and Tensor Products for Matrices

Saburou Saitoh

Institute of Reproducing Kernels, Kiryu, Japan.

DOI: 10.4236/alamt.2014.42006                

Abstract

We shall give natural generalized solutions of Hadamard and tensor products equations for matrices by the concept of the Tikhonov regularization combined with the theory of reproducing kernels.

Keywords

Reproducing Kernel, Positive Definite Hermitian Matrix, Tensor Product, Hadamard Product, Generalized Inverse, Matrix Equation, Tikhonov Regularization, 100/0 = 0, 0/0 = 0, Generalized Fraction, Generalized Fractional Function

1. Introduction

In this paper we shall consider the matrix equation

(1)

however, here we shall consider the product

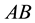(2)

in the two senses; that is, the Hadamard product

(3)

and the tensor (Kronecker) product

(4)

Then, for the Hadamard product, for some same type matrices, the product may be considered as the matrix 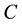made by each matrix elements-wise products, meanwhile, for the tensor product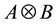, there is no any restriction on the matrices types. In this paper, we shall consider natural inversions for given 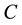and by the idea of the Tikhonov regularization and the Moore-Penrose generalized inverses from the viewpoint of the theory of reproducing kernels.

2. Needed Backgrounds

We shall need the basic theory of reproducing kernels in connection with matrices. We shall fix the minimum requests for our purpose.

2.1. Reproducing Kernels and Positive Definite Hermitian Matrices

Let 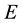be an arbitrary abstract (non-void) set. Let 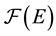denote the set of all complex-valued functions on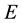. A reproducing kernel Hilbert spaces (RKHS for short) on the set is a Hilbert space endowed with a function, which is called the reproducing kernel and which satisfies the reproducing property. Namely we have

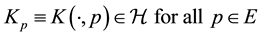(5)

and

(6)

for all and for all. We denote by (or) the reproducing kernel Hilbert space whose corresponding reproducing function is.

A complex-valued function is called a positive definite quadratic form function on the set, or shortly, positive definite function, if, for an arbitrary function and for any finite subset of, one has

(7)

By a fundamental theorem, we know that, for any positive definite quadratic form function on, there exists a unique reproducing kernel Hilbert space on with reproducing kernel. So, in a sense, the correspondence between the reproducing kernel and the reproducing kernel Hilbert space is one to one.

A simple example of positive definite quadratic form function is a positive definite Hermitian matrix and we obtain the fundamental relation:

Example 2.1 Let be a set consisting of distinct points. Let be a strictly positive Hermitian matrix. Let denote the inverse of. Then the space of the complex valued functions on, endowed with the inner product

is a reproducing kernel Hilbert (complex Euclidean) space with reproducing kernel defined by for all.

Indeed, the validity of (5) follows by a straightforward calculation. To prove (6) we observe that

for all (note that). Thus coincides with the reproducing kernel Hilbert space. In particular the norm induced by the product coincides with the norm of.

We can thus combine the two theories of positive definite Hermitian matrices and of reproducing kernels. See [1] -[9] for various applications and numerical problems.

2.2. Tensor Products of Reproducing Kernel Hilbert Spaces and Restrictions

For any two positive definite quadratic form functions and on and, respectively, the usual product is again a positive definite quadratic form function on. Then, it is the reproducing kernel for the tensor product for their reproducing kernel Hilbert spaces.

We would like to recall that for any two positive definite quadratic form functions and on, the usual product is again a positive definite quadratic form function on. Consequently, the reproducing kernel Hilbert space which admits the kernel can be seen as the restriction of the tensor product to the diagonal set.

Proposition 2.1 (see, [10] [11] ) Let us consider and to be complete orthonormal systems in and, respectively. Then, the reproducing kernel Hilbert space is comprised of all functions on which are represented by

(8)

in the sense of absolutely convergence on, and its norm in is given by

where are considered to satisfy (8). Moreover, the norm inequality

holds true.

2.3. Generalized Inverses and the Tikhonov Regularization

Let be any bounded linear operator from a reproducing kernel Hilbert space into a Hilbert space. Then, the following problem is a classical and fundamental problem (known as the best approximate mean square norm problem): For any member of, we would like to find

It is clear that we are considering operator equations, generalized solutions and corresponding generalized inverses within the framework of and, having in mind the equation

(9)

However, this problem has a complicated structure, specially in the infinite dimensional Hilbert spaces case, leading in fact to the consideration of generalized inverses (in the Moore-Penrose sense). Anyway, the problem turns to be well-posed within the reproducing kernels theory framework in the following proposition:

Proposition 2.2 For any member of, there exists a function in satisfying

(10)

if and only if, for the reproducing kernel Hilbert space, admitting the kernel defined by we have

(11)

Furthermore, when there exists a function satisfying (10), there exists a uniquely determined function that minimizes the norms in among the functions satisfying the equality, and its function is represented as follows:

(12)

From this proposition, we see that the problem is considered in a very good way by the theory of reproducing kernels. Namely, the existence, uniqueness and representation of the solutions for this problem are well- formulated. In particular, note that the adjoint operator is represented in a useful way (which will be very important in our framework later on). The extremal function is the Moore-Penrose generalized inverse of the equation. The criteria (11) is involved and so the Moore-Penrose generalized inverse is―in general―not good, specially when the data contain error or noises in some practical cases. To overcome this difficulty, we will need the idea of Tikhonov regularization.

Proposition 2.3 Let be a bounded linear operator defined from any reproducing kernel Hilbert space into any Hilbert space, and define the inner product

for. Then is a reproducing kernel Hilbert space whose reproducing kernel is given by

Here, is the uniquely determined solution of the functional equation

(13)

(that is corresponding to the Fredholm integral equation of the second kind for many concrete cases). Moreover, we are using

Proposition 2.4 The Tikhonov functional

attains the minimum and the minimum is attained only by the function such that

(14)

Furthermore, satisfies

(15)

For up-to-date versions of the Tikhonov regularization by using the theory of reproducing kernels, see [12] [13] . Furthermore, various applications and numerical problems, see, for example, [14] [15] .

2.4. The Solution of the Tikhonov Functional Equation

For our purpose, we use a natural representation of the Tikhonov extremal function considered in Proposition 2.4 by using complete orthogonal systems in the Hilbert spaces and. The original result is given by [16] .

Let and be any fixed complete orthonormal systems of the Hilbert spaces and, respectively.

Therefore, from the form (13) and the representation (14) in Proposition 2.4 of the Tikhonov extremal function, we shall assume the representation

(16)

in the sense of the tensor product.

In the expansion of the reproducing kernel,

(17)

since belongs to, we can set

(18)

with the uniquely determined constants satisfying, for any fixed,

Note that the natural condition

(19)

is equivalent to the circumstance of the operator be a Hilbert-Schmidt operator from into.

By setting

we consider the infinite equations

(20)

Then, we obtain:

Proposition 2.5 Assume that the operator is a Hilbert-Schmidt operator and the Equation (20) have the solutions satisfying

(21)

Then, for any, the Tikhonov extremal function in the sense of Proposition 2.4 is given by

(22)

and the following fundamental estimates hold:

and

(23)

Here, note that are depending on.

In particular, if is finite dimensional, the infinite Equation (20) are solved explicitly and so, then, it is enough to check the convergence (21).

Of course, if both spaces and are finite dimensional, then we obtain the complete representation for the Tikhonov extremal function.

Meanwhile, when we apply the above complete orthonormal systems to the Moore-Penrose generalized problem, we see that we cannot, in general, obtain any valuable information, because we cannot analyze the structure of the important reproducing kernel Hilbert space in Proposition 2.2.

3. Matrices and Reproducing Kernels

We shall combine matrices and reproducing kernels. In order to simplify the notations we shall consider the numbers on the real field.

First note that is the reproducing kernel Hilbert space admitting the reproducing kernel that is represented by the unit matrix of the and then the inner product in is given by

and when we take the simplest standard orthonormal system, the reproducing property is given by

and

We shall consider another space , similarly and we shall consider the tensor product. Then, the metric in the tensor product is given by

for

in the dimensional space for

and

This will mean that the matrices formed by, for and

(24)

form the tensor product of the two reproducing spaces and and the metric is introduced by the in the dimensional space and the reproducing kernel may be considered as in the case.

By this idea, we can consider any matrices space of any type may be considered as reproducing kernel spaces and when we consider the metric, we shall consider it as in the above sense. As we stated in the introduction, since we are interested in the Hadamard product and tensor product of matrices, we will see that it is enough to consider the case of vector spaces by transformed to vectors.

4. Hadamard Product Inversions

We shall consider on and for any members, in the Hadamard product

we shall consider the Tikhonov inverse in the sense, for any positive and for any

(25)

Then, we obtain

Theorem 4.1 In the sense of (25), the general inversion is given by

Proof. Note that from the general theory of reproducing kernels, we obtain the inequality

However, this is just the Cauchy-Schwart inequality and the theory gives the background of the inequality with the precise structure of the Hadamard product. So, the multiplication operator, for any fixed

is a bounded linear operator and by Proposition 2.5, directly we obtain the result.

Of course, there exists a uniquely determined the Moore-Penrose generalized inverse, all the cases, by taking the limit

(26)

In particular, in the sense of the Moore-Penrose generalized inverse, of course, we have, on,

(27)

Mathematicians will expect for our mathematics, there exists some realization of our mathematics in some real world. So, we wonder: does there exist some real examples supporting the above results.

In particular, Sin-Ei,Takahashi ([17] ) established a simple and natural interpretation (27) by analyzing any extensions of fractions and by showing the complete characterization for such property (27). His result will show that our mathematics says that the results (27) should be accepted as natural ones. However, the results will be curious and so, the above question will be vital still as a very important problem.

For simple direct proofs and several physical meanings, see [18] .

5. Inversions of Tensor Products of Matrices

Before a general situation, we shall show the simplest case as a prototype example in order to see the basic concept and problem for the inversion. We shall consider for and as follows:

(28)

(29)

We can write the tensor product as follows:

(30)

or with its transpose. However, as we stated, we shall consider it as follows:

(31)

Now we are interested in the matrix equation, for given

(32)

that will mean the equations:

(33)

We are considering arbitrary positive integers, and so we see that these equations will have important problems; the existence and representation problems. By the concept and theory in Proposition 2.5, we will be able to obtain the reasonable solutions.

For any members and, we shall consider the Tikhonov inverse in the sense, for any positive

(34)

Note that from the general theory of reproducing kernels, we obtain the equality

That is, for any fixed, the operator

is a bounded linear operator into. So, we can apply Proposition 2.5.

The Equation (16) corresponds to

(35)

The representation (18) corresponds to

(36)

with the uniquely determined constants, for any fixed. We set

We consider the equations as in (20)

(37)

Then, we obtain

Theorem 5.1 In the sense of (34), the general inversion is given, with the uniquely determined solutions of the Equation (37)

and the corresponding results in Proposition 2.5 are valid.

Acknowledgements

The author wishes to express his sincere thanks to Dr. Masako Takagi for her careful readings of the manuscript and her kind suggestions. The author is supported in part by the Grant-in-Aid for the Scientific Research (C) (2) (No. 24540113).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Asaduzzaman, M. and Saitoh, S. (2003) Inverses of a Family of Matrices and Generalizations of Pythagorean Theorem. Panamerican Mathematical Journal, 13, 45-53.
[2]	Mai, W., Yan, M., Qian, T., Riva, M.D. and Saitoh, S. (1013) A Matrix Inequality for the Inversions of the Restrictions of a Positive Definite Hermitian Matrix. Advances in Linear Algebra & Matrix Theory, 3, 55-58.
[3]	Mond, B., Pecaric, J.E. and Saitoh, S. (1994) History, Variations and Generalizations of an Inequality of Marcus. Riazi: Journal of Karachi Mathematical Association, 16, 7-15.
[4]	Saitoh, S. (1982) Positive Definite Hermitian Matrices and Reproducing Kernels. Linear Algebra and Its Applications, 48, 119-130. http://dx.doi.org/10.1016/0024-3795(82)90102-1
[5]	Saitoh, S. (1987) Quadratic Inequalities Deduced From the Theory of Reproducing Kernels. Linear Algebra and Its Applications, 93, 171-178. http://dx.doi.org/10.1016/S0024-3795(87)90322-3
[6]	Saitoh, S. (1988) Quadratic Inequalities Associated with Integrals of Reproducing Kernels. Linear Algebra and Its Applications, 101, 269-280. http://dx.doi.org/10.1016/0024-3795(88)90154-1
[7]	Saitoh, S. (2003) Generalizations of the Triangle Inequality. Journal of Inequalities in Pure and Applied Mathematics, 4, Article 62.
[8]	Sawano, Y. (2011) Pasting Reproducing Kernel Hilbert Spaces. Jaen Journal on Approximation, 3, 135-141.
[9]	Yamada, A. (2012) Oppenheim’s Inequality and RKHS. Mathematical Inequalities and Applications, 15, 449-456.
[10]	Saitoh, S. (1997) Integral Transforms, Reproducing Kernels and their Applications. Pitman Research Notes in Math. Series 369, Addison Wesley Longman, Harlow.
[11]	Saitoh, S. (2010) Theory of Reproducing Kernels: Applications to Approximate Solutions of Bounded Linear Operator Functions on Hilbert Spaces. American Mathematical Society Translations: Series 2, 230, Amer. Math. Soc., Providence, RI.
[12]	Castro, L.P., Fujiwara, H., Saitoh, S., Sawano, Y., Yamada, A. and Yamada, M. (2012) Fundamental Error Estimates Inequalities for the Tikhonov Regularization Using Rreproducing Kernels. International Series of Numerical Mathematics 161, Inequalities and Appications 2010, Springer, Basel, 87-101.
[13]	Castro, L.P., Saitoh, S., Sawano, Y. and Silva, A.S. (2012) Discrete Linear Differential Equations. Analysis, 32, 181- 191. http://dx.doi.org/10.1524/anly.2012.1104
[14]	Castro, L.P., Fujiwara, H., Rodrigues, M. M., Saitoh, S. and Tuan, V.K. (2014) Aveiro Discretization Method in Mathematics: A New Discretization Principle. In: Pardalos, P. and Rassias, T.M., Eds., Mathematics without Boundaries: Surveys in Pure Mathematics, in press.
[15]	Castro, L.P., Fujiwara, H., Qian, T. and Saitoh, S. (2014) How to Catch Smoothing Properties and Analyticity of Functions by Computers? In: Pardalos, P. and Rassias, T.M., Eds., Mathematics without Boundaries: Surveys in Interdisipinary Research, in press.
[16]	Castro, L. P., Saitoh, S. and Yamada, A. (2014) Representations of Solutions of Tichhonov Functional Equations and Applications to Multiplication Operators of the Szego Spaces (submitted).
[17]	Takahashi, S. (2014) On the Identities 100/0=0 and 0/0=0. (submitted).
[18]	Kuroda, T., Michiwaki, H., Saitoh, S. and Yamane, M. (2014) New Meanings of the Division by Zero and Interpretations on 100/0 = 0 and on 0/0 = 0. International Journal of Applied Mathematics, 27, 191-198.