1. Introduction
1.1. Problem Definition
We are given a bipartite graph  where each edge
where each edge  has one endpoint in
has one endpoint in  and the other endpoint in
and the other endpoint in . Elements of
. Elements of  are normally referred as agents (or people), and elements of
are normally referred as agents (or people), and elements of  are referred as tasks (or jobs). Then
are referred as tasks (or jobs). Then  means that agent
means that agent  can perform task
can perform task  (not every agent can perform every task). In classic maximum bipartite matching problem the goal is to find a matching in
(not every agent can perform every task). In classic maximum bipartite matching problem the goal is to find a matching in  (a set of pairwise non-adjacent edges) that contains the largest possible number of edges. A matching is a one-to-one assignment: each agent can be assigned to at most one task, and each task can be assigned to at most one agent.
(a set of pairwise non-adjacent edges) that contains the largest possible number of edges. A matching is a one-to-one assignment: each agent can be assigned to at most one task, and each task can be assigned to at most one agent.
We consider the following variation of the maximum bipartite matching problem. Each agent still can be assigned to at most one task. But in our problem a task can be completed only if at least two agents are assigned to it. The goal is to maximize the number of completed tasks.
The problem can be given by the following integer program (IP):
 (1)
(1)
 (2)
(2)
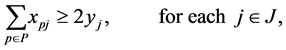 (3)
(3)
 (4)
(4)
Here  is the set of agents,
is the set of agents,  is the set of tasks.
is the set of tasks. 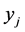 is a binary variable which is equal to 1 if task
is a binary variable which is equal to 1 if task  is completed.
is completed. 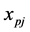 is a binary variable which is equal to 1 if agent
is a binary variable which is equal to 1 if agent  is assigned to task
is assigned to task . The objective of Function (1) is trying to maximize the number of completed tasks. Constraint (2) provides that each agent is assigned to no more than one task. Constraint (3) provides that if a task is completed then at least two agents are assigned to it.
. The objective of Function (1) is trying to maximize the number of completed tasks. Constraint (2) provides that each agent is assigned to no more than one task. Constraint (3) provides that if a task is completed then at least two agents are assigned to it.
1.2. Applications
The problem was first considered in [1] as a solution method for a combinatorial problem related to circuit reduction. [1] gave an integer program for the problem. In this paper we give a more efficient solution method based on the LP-relaxation of the integer program.
A few typical examples of the problem are given below. A group has members (agents) who should be assigned to projects (tasks). Each member can work only on some of the projects based on her/his qualifications. A project can be pursued only if at least two members are assigned to it. The goal is to maximize the number of projects that are pursued.
In a variation of the facility location problem, potential facility sites are the tasks, and demand points are the agents. Not every potential facility can serve every demand point (based on distance, compatibility, etc.). It is economical to open a facility only if it is assigned to serve at least two demand points. The goal is to maximize the number of open facilities.
Another possible situation is in the following. A company should assign guides to several tourist groups (tasks). Each group is from a certain country and needs guides who speak their language. The company has several guides (agents); each guide speaks several languages. Each group should be assigned two guides (primary and backup) satisfying the language requirement. The goal is to maximize the number of possible assignments.
1.3. Literature Review
Matching and assignment problems are of great importance in graph theory and combinatorial optimization ([2] [3] [4] ). The history of development, applications and solution methods of matching and assignment problems are discussed in [4] . Some variations of matching problems are discussed in [5] . A survey of assignment problems is given in [6] . In most variations the goal is to find a one-to-one assignment subject to some kind of restrictions. But some variations allow assignments of multiple agents to the same task or multiple tasks to the same agent ([7] -[9] ). The generalized assignment problem ([8] ) allows an agent to do multiple tasks provided that the set of tasks assigned to an agent do not exceed its capacity. In [7] an agent can be assigned several tasks, and the goal is to find an assignment that minimizes the total time of completing all the tasks.
Our model was introduced in [1] . To the best of our knowledge, no other model has considered the variation that a task can be completed only if two or more agents are assigned to it.
1.4. Our Results
The maximum bipartite matching problem can be solved by network flow techniques. It can be formulated as a maximum flow problem and solved by the augmenting path algorithm. Another solution method is linear programming. The constraint matrix of its integer program is totally unimodular, and thus the LP-relaxation returns integer solutions.
Those results do not extend to our problem. It is not clear how to use maximum flow techniques to solve the paired assignment problem. And as we show in Section 2, the constraint matrix of its integer program is not totally unimodular. But in the same section we show that any basic solution of the LP relaxation is half-integral; more specifically, each  variable is integral, and each
variable is integral, and each  variable is half-integral. We use this special structure of basic solutions to design an algorithm that takes a half-integral basic solution as a starting point and gradually increases the number of completed tasks. The procedure to accomplish it is a modified version of breadth-first search. We prove that the algorithm returns an optimal solution for the paired assignment problem.
variable is half-integral. We use this special structure of basic solutions to design an algorithm that takes a half-integral basic solution as a starting point and gradually increases the number of completed tasks. The procedure to accomplish it is a modified version of breadth-first search. We prove that the algorithm returns an optimal solution for the paired assignment problem.
1.5. Outline of Paper
The paper is structured as follows. In Section 2, we show that any basic solution of the LP relaxation of (IP) is half-integral. In Section 3, we show how the basic solutions can be further processed to increase the number of completed tasks. In Section 4, we give an algorithm for solving the paired assignment problem and show that it returns an optimal solution. Future directions are discussed in Section 5.
2. Description of Basic Solutions of LP-Relaxation
The linear programming relaxation (LP) of the integer program (IP) is obtained by replacing the binary requirements of  and
and  with
with  and
and  .
.
Theorem 1 Basic solutions of (LP) are half-integral. Specifically, every  variable is integer, and every
variable is integer, and every  variable takes value 0, 0.5, or 1.
variable takes value 0, 0.5, or 1.
Proof: Suppose the functional constraints of (LP) are rewritten in a standard form .
.
The coefficient matrix of Constraints (2) and (3) has the following form:

where
•  represents the coefficients of
represents the coefficients of  variables in Constraints (2);
variables in Constraints (2);
•  represents the coefficients of
represents the coefficients of  variables in Constraints (3);
variables in Constraints (3);
•  represents the coefficients of
represents the coefficients of  variables in Constraints (3).
variables in Constraints (3).
Matrix  is totally unimodular because each column has exactly one 1 and one –1. Matrix
is totally unimodular because each column has exactly one 1 and one –1. Matrix  is a diagonal matrix with 2’s on the main diagonal.
is a diagonal matrix with 2’s on the main diagonal.
Suppose  is a basis matrix for the augmented form of
is a basis matrix for the augmented form of . Then the corresponding basic solution can be computed as follows:
. Then the corresponding basic solution can be computed as follows:
 .
.
Next we evaluate . First we expand by the columns of slack variables; in the result all the rows that correspond to basic slack variables will be crossed out. Then we expand by the columns of
. First we expand by the columns of slack variables; in the result all the rows that correspond to basic slack variables will be crossed out. Then we expand by the columns of  variables. Consider the following cases.
variables. Consider the following cases.
Case 1. Suppose we expand by a column of a  variable that takes a fractional value in the basic solution. Then the slack variables of both
variable that takes a fractional value in the basic solution. Then the slack variables of both  and
and 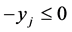 are basic, and thus both rows were crossed out in earlier expansions. So there is only one non-zero entry left in the column of
are basic, and thus both rows were crossed out in earlier expansions. So there is only one non-zero entry left in the column of , namely 2 in corresponding Constraint (3). Thus, the expansion will result in 2 times the corresponding cofactor.
, namely 2 in corresponding Constraint (3). Thus, the expansion will result in 2 times the corresponding cofactor.
Case 2. Suppose we expand by a column of a  variable that takes value 1 in the basic solution. Then the slack variable of
variable that takes value 1 in the basic solution. Then the slack variable of  is basic, and thus the corresponding row was crossed out earlier. There are two non-zero entries in the column of
is basic, and thus the corresponding row was crossed out earlier. There are two non-zero entries in the column of : 2 in corresponding Constraint (3) and 1 in
: 2 in corresponding Constraint (3) and 1 in . The minor of entry 2 is 0 since after crossing its column only 0's are left in the row of
. The minor of entry 2 is 0 since after crossing its column only 0's are left in the row of . Thus, the expansion will include only one non-zero term, which is 1 times the corresponding cofactor.
. Thus, the expansion will include only one non-zero term, which is 1 times the corresponding cofactor.
Case 3. Suppose we expand by a column of a 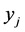 variable that takes value 0 in the basic solution. Then the slack variable of
variable that takes value 0 in the basic solution. Then the slack variable of  is basic, and thus the corresponding row was crossed out earlier. There are two non-zero entries in the column of
is basic, and thus the corresponding row was crossed out earlier. There are two non-zero entries in the column of : 2 in corresponding Constraint (3) and –1 in
: 2 in corresponding Constraint (3) and –1 in . The minor of entry 2 is 0 since after crossing its column only 0's are left in the row of
. The minor of entry 2 is 0 since after crossing its column only 0's are left in the row of . Thus, the expansion will include only one non-zero term, which is -1 times the corresponding cofactor.
. Thus, the expansion will include only one non-zero term, which is -1 times the corresponding cofactor.
The matrix obtained after crossing out all basic  columns with corresponding rows is totally unimodular as a submatrix of a classic assignment problem. Thus, based on Cases (1)-(3),
columns with corresponding rows is totally unimodular as a submatrix of a classic assignment problem. Thus, based on Cases (1)-(3),  is either
is either  or
or  where
where  is the number of
is the number of  variables that take fractional values in the basic solution.
variables that take fractional values in the basic solution.
Next, for each different type of variable, we evaluate  and the value of the variable.
and the value of the variable.
Consider a basic variable .
.
Suppose  is an element in the column of
is an element in the column of  in a constraint of type (2) or (4). Then after crossing its column and row we still have 2’s in all basic
in a constraint of type (2) or (4). Then after crossing its column and row we still have 2’s in all basic  -columns. Thus, the above analysis on
-columns. Thus, the above analysis on  still applies here, and the cofactor of
still applies here, and the cofactor of  is either
is either  or
or . Then the corresponding additive term in
. Then the corresponding additive term in  is 0,
is 0,  , or
, or  since we have only 0's and 1's in
since we have only 0's and 1's in .
.
Suppose  is an element in the column of
is an element in the column of  in a constraint of type (3). The right-hand side of the constraint in the standard form is 0. Thus, the corresponding additive term in
in a constraint of type (3). The right-hand side of the constraint in the standard form is 0. Thus, the corresponding additive term in  is also 0.
is also 0.
Summarizing, all the additive terms in  are 0,
are 0,  , or
, or . Thus,
. Thus,  can take only integer values since
can take only integer values since  is either
is either 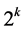 or
or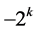 .
.
Consider a basic variable .
.
Suppose  is an element in
is an element in ’s column. Submatrix
’s column. Submatrix  obtained by crossing its column and row has only one 2 less than the original matrix
obtained by crossing its column and row has only one 2 less than the original matrix . Thus, if we repeat the analysis done in Cases (1)-(3) for
. Thus, if we repeat the analysis done in Cases (1)-(3) for  we can have the following possible values for its determinant:
we can have the following possible values for its determinant:  or
or  if
if  takes an integer value,
takes an integer value,  or
or  if
if  takes a fractional value. Then the corresponding additive term in
takes a fractional value. Then the corresponding additive term in  is 0,
is 0, 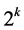 ,
,  ,
,  , or
, or  since we have only 0’s and 1’s in
since we have only 0’s and 1’s in . Thus, the only values
. Thus, the only values  can take are 0, 0.5, and 1 since
can take are 0, 0.5, and 1 since  is either
is either 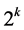 or
or . ,
. ,
3. Increasing Number of Completed Tasks by Reassignment
Suppose we have a solution to (LP). Based on Theorem 1, each  variable takes one of the following values, 0, 0.5, or 1. Correspondingly, we distinguish three types of task-nodes in the current solution.
variable takes one of the following values, 0, 0.5, or 1. Correspondingly, we distinguish three types of task-nodes in the current solution.
Definition 1 A task-node is called
• completed if the corresponding ;
;
• incomplete if the corresponding ;
;
• unassigned if the corresponding .
.
Suppose we have a half-integral solution. It would be reasonable to include the completed tasks in the solution. But simply including the completed tasks might not give a good solution. Consider the example 1 of Figure 1. We will have the following convention for the rest of paper. Any arc that takes value 1 in the LP-relaxation will be called red arc and will be colored red (bold) in our figures; any arc that takes value 0 in the LP-relaxation will be called blue arc and will be colored blue in our figures. In the example of Figure 1, an optimal basic solution has no task with two agents assigned to it (both  and
and  are 0.5). But we can clearly have one completed task by assigning both
are 0.5). But we can clearly have one completed task by assigning both  and
and  to
to  as it is done in Figure 2.
as it is done in Figure 2.
In order to increase the number of completed tasks we need a reassignment from the current solution. The following result provides a general strategy for such a reassignment.
Lemma 1 Any reassignment that increases the number of completed tasks will decrease the number of incomplete tasks by at least two.
Proof: Suppose there are  completed and
completed and  incomplete tasks in the current solution with LP-value
incomplete tasks in the current solution with LP-value . Recall that
. Recall that  is the optimal value of the LP-relaxation. Suppose there is another solution with at least
is the optimal value of the LP-relaxation. Suppose there is another solution with at least  completed tasks. Since the LP-value of any feasible solution cannot be more than
completed tasks. Since the LP-value of any feasible solution cannot be more than 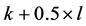 then the number of incomplete tasks in the new solution is no more than
then the number of incomplete tasks in the new solution is no more than . Lemma 1 implies that incomplete tasks should be the key in any reassignment that increases the number of
. Lemma 1 implies that incomplete tasks should be the key in any reassignment that increases the number of

Figure 1. Original solution for example 1.

Figure 2. Reassigned solution for example 1.
completed tasks. To get some insight how such an increase can be achieved consider example 2 given in Figure 3 and Figure 4 and example 3 given in Figure 5 and Figure 6.
In Figure 3, tasks  and
and  are incomplete, and task
are incomplete, and task  is completed. By reassigning agents, as it is done in Figure 4,
is completed. By reassigning agents, as it is done in Figure 4,  becomes completed and
becomes completed and  unassigned, thus increasing the number of completed tasks from 1 to 2.
unassigned, thus increasing the number of completed tasks from 1 to 2.
In Figure 5, tasks  and
and  are incomplete, task
are incomplete, task  is completed, and
is completed, and  is unassigned. By reassigning agents, as it is done in Figure 6,
is unassigned. By reassigning agents, as it is done in Figure 6,  and
and  become completed, and
become completed, and  and
and  become unassigned, thus increasing the number of completed tasks from 1 to 2.
become unassigned, thus increasing the number of completed tasks from 1 to 2.
We need the following definition to discuss the common pattern in the above examples.
Definition 2 Let 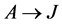 and
and  be two arcs with the same agent-node
be two arcs with the same agent-node  as origin. If in a current solution
as origin. If in a current solution 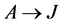 is red (assigned) and
is red (assigned) and  is blue (unassigned) then we call
is blue (unassigned) then we call  a red-blue arc pair.
a red-blue arc pair.
All our examples, where we were able to create more completed tasks by reassignment, have the following feature. There are two incomplete tasks which are connected by a sequence of red-blue arc pairs. The number of completed tasks is increased by recoloring those red-blue pairs of arcs: the red arcs become blue, and the blue arcs become red. Recoloring the arcs essentially means reassigning every agent-node in the sequence to a different task.
In example 2, the original sequence is  which becomes
which becomes  after recoloring. In example 3, the sequence is
after recoloring. In example 3, the sequence is  which becomes
which becomes  after recoloring.
after recoloring.
The increase in number of completed tasks happens because the task-nodes in sequences change their statuses. In our examples, an unassigned task becomes assigned (e.g., task  in example 3); incomplete nodes can become completed (e.g., task
in example 3); incomplete nodes can become completed (e.g., task  in example 2) or unassigned (e.g., task
in example 2) or unassigned (e.g., task  in example 2); completed tasks can become unassigned (e.g., task
in example 2); completed tasks can become unassigned (e.g., task  in example 3) or stay completed (e.g., task
in example 3) or stay completed (e.g., task  in example 2).
in example 2).
But we do not have a completed task-node with both incident arcs blue in the original sequence. It would mean that the two agents assigned to the task are not in the sequence. Thus, by recoloring we would assign two more agents to a task which is already completed. In that case it is unlikely that we would increase the number of completed tasks by reassignment.
The above analysis of the patterns observed in our examples leads to the following important concept.
Definition 3 A sequence  of red-blue arc pairs, that connects two incomplete task-nodes, is called a valid path if
of red-blue arc pairs, that connects two incomplete task-nodes, is called a valid path if
• there are no interior incomplete nodes on ;
;
• any interior completed node on  has at least one incident red arc in the sequence.
has at least one incident red arc in the sequence.
Using the concept of valid path, the following result generalizes the strategy of increasing the number of completed tasks observed in our examples.
Theorem 2 If there is a valid path connecting two incomplete task-nodes in a half-integral solution then we can increase the number of completed tasks by 1 by recoloring all the arcs on the path.
Proof: Let  and
and  be incomplete task-nodes that are connected by a valid path
be incomplete task-nodes that are connected by a valid path . We want to show that the number of completed tasks is increased by recoloring all the arcs on
. We want to show that the number of completed tasks is increased by recoloring all the arcs on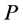 .
.
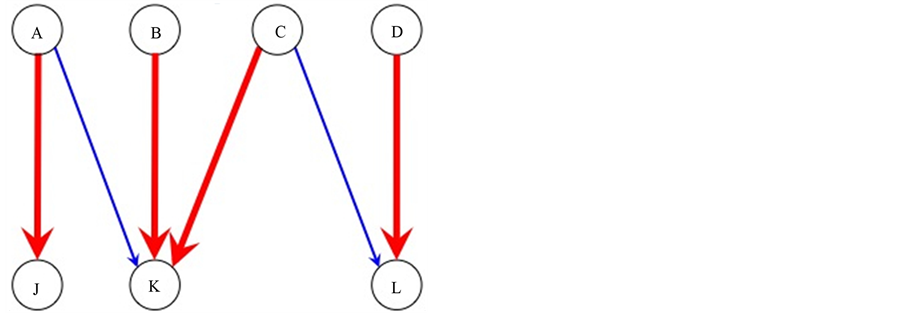
Figure 3. Original solution for example 2.
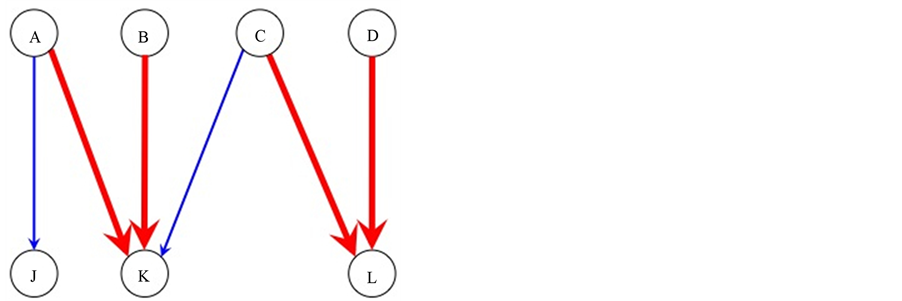
Figure 4. Reassigned solution for example 2.

Figure 5. Original solution for example 3.
First we categorize the task-nodes on , and describe how recoloring will change their statuses.
, and describe how recoloring will change their statuses.
1) If  is an unassigned node then it has two incident blue arcs on
is an unassigned node then it has two incident blue arcs on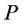 . Thus, recoloring will make both arcs red, and
. Thus, recoloring will make both arcs red, and 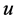 will become a completed node (e.g., task
will become a completed node (e.g., task  in example 3).
in example 3).
2) If  is an incomplete node and its incident arc on
is an incomplete node and its incident arc on  is blue then recoloring the arc will make
is blue then recoloring the arc will make  completed (e.g., task
completed (e.g., task  in example 2).
in example 2).
3) If 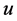 is an incomplete node and its incident arc on
is an incomplete node and its incident arc on  is red then recoloring the arc will make
is red then recoloring the arc will make  unassigned (e.g., task
unassigned (e.g., task  in example 2).
in example 2).
4) If  is a completed node with two incident red arcs on
is a completed node with two incident red arcs on  then recoloring will make both arcs blue. Thus,
then recoloring will make both arcs blue. Thus, 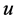 will become an unassigned node (e.g., task
will become an unassigned node (e.g., task  in example 3).
in example 3).

Figure 6. reassigned solution for example 3.
5) If  is a completed node with one incident red arc and one incident blue arc on
is a completed node with one incident red arc and one incident blue arc on  then after recoloring
then after recoloring  will stay completed with one incident blue arc and one one incident red arc on
will stay completed with one incident blue arc and one one incident red arc on  (e.g., task
(e.g., task  in example 2).
in example 2).
Note that we cannot have a completed node with two incident blue arcs on  since
since  is a valid path.
is a valid path.
As discussed above, only type (5) nodes do not change their status in the result of recoloring. Thus, our goal is to find out how status changes in other type of nodes affect the number of completed tasks on . To answer that question we need to discuss the possible configurations of type (1)-(4) nodes on
. To answer that question we need to discuss the possible configurations of type (1)-(4) nodes on .
.
Suppose  and
and  are task-nodes of type (1)-(4) on
are task-nodes of type (1)-(4) on . We say
. We say  and
and  are
are  -neighbors if all the internal task-nodes (if any) on the subpath of
-neighbors if all the internal task-nodes (if any) on the subpath of  joining
joining  and
and  are type (5) nodes. Based on the definition of type (5) nodes, any two neighboring arcs on the subpath joining two
are type (5) nodes. Based on the definition of type (5) nodes, any two neighboring arcs on the subpath joining two  -neighbors have different colors. Also, based on their definitions, type (1) and (2) nodes have only incident blue arcs on
-neighbors have different colors. Also, based on their definitions, type (1) and (2) nodes have only incident blue arcs on  while type (3) and (4) nodes have only incident red arcs on
while type (3) and (4) nodes have only incident red arcs on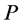 . Based on the last two observations, we have the following intermediate result.
. Based on the last two observations, we have the following intermediate result.
Lemma 2 Any node of type (1) or (2) can be a  -neighbor only with a node of type (3) or (4), and conversely, any node of type (3) or (4) can be a
-neighbor only with a node of type (3) or (4), and conversely, any node of type (3) or (4) can be a  -neighbor only with a node of type (1) or (2). In other words, on
-neighbor only with a node of type (1) or (2). In other words, on , type (1) or (2) nodes are alternated by type (3) or (4) nodes.
, type (1) or (2) nodes are alternated by type (3) or (4) nodes.
Now we are ready to discuss how the number of completed tasks will be changed in the result of recoloring. We have three possible cases.
Case 1: Both incomplete nodes  and
and  on
on  are of type 3. Based on Lemma 2, the number of type (1) nodes on
are of type 3. Based on Lemma 2, the number of type (1) nodes on  is more than the number of type (4) nodes on
is more than the number of type (4) nodes on  exactly by 1. After recoloring, incomplete nodes
exactly by 1. After recoloring, incomplete nodes  and
and  become unassigned, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
become unassigned, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
Case 2: Both incomplete nodes  and
and 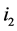 on
on  are of type 2. Based on Lemma 2, the number of type (4) nodes on
are of type 2. Based on Lemma 2, the number of type (4) nodes on  is more than the number of type (1) nodes on
is more than the number of type (1) nodes on  exactly by 1. After recoloring, both
exactly by 1. After recoloring, both  and
and  become completed, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
become completed, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
Case 3: One of  and
and 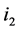 is of type 2, and the other one is of type 3. Based on Lemma 2, the number of type (4) nodes on
is of type 2, and the other one is of type 3. Based on Lemma 2, the number of type (4) nodes on  is equal to the number of type (1) nodes on
is equal to the number of type (1) nodes on . After recoloring, the incomplete node which is of type (2) will become completed, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
. After recoloring, the incomplete node which is of type (2) will become completed, each type (1) (unassigned) node becomes completed, and each type (4) (completed) node becomes unassigned. Thus, the number of completed nodes is increased exactly by 1.
Summarizing, in any case the number of completed nodes is increased exactly by 1. This concludes the proof of theorem 2. ,
4. Algorithm for Paired Assignment Problem
The result of Theorem 2 is the basis of the following algorithm for solving the paired assignment problem.
Algorithm 4.1 Algorithm for Paired Assignment Solve the LP-relaxation of the problem while there is a valid path connecting two incomplete task-nodes do recolor all the arcs along the valid path end while In the next two subsections we show that: 1) a valid path can be found efficiently using a modified version of breadth-first search (BFS); 2) the algorithm returns an optimal solution for the problem.
4.1. Procedure for Finding a Valid Path
We need to define an auxiliary digraph to do the search. For each red-blue pair of arcs  we define a directed arc
we define a directed arc  connecting the task-nodes by choosing the direction of the red arc. Let
connecting the task-nodes by choosing the direction of the red arc. Let  be the set of all directed arcs defined this way (note that two directed arcs
be the set of all directed arcs defined this way (note that two directed arcs  and
and  might have their original blue-red pairs sharing the red arc). Then we have a digraph
might have their original blue-red pairs sharing the red arc). Then we have a digraph  defined on the set of all tasks
defined on the set of all tasks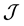 . For example, the digraph corresponding to the original graph of Figure 5 is
. For example, the digraph corresponding to the original graph of Figure 5 is .
.
The search of a valid path can be done in . The equivalent of a valid path in
. The equivalent of a valid path in  is an undirected path
is an undirected path  connecting two incomplete nodes such that
connecting two incomplete nodes such that
• there are no interior incomplete nodes on ;
;
• any interior completed node on  has at least one of its incident arcs incoming.
has at least one of its incident arcs incoming.
The modified BFS for finding a valid path in  is done as follows. One of the incomplete nodes, say
is done as follows. One of the incomplete nodes, say , is chosen to be the root node. The modification to BFS concerns the completed nodes in the queue.
, is chosen to be the root node. The modification to BFS concerns the completed nodes in the queue.
• If a completed node  is reached from its parent-node
is reached from its parent-node  in the queue through an incoming arc
in the queue through an incoming arc  then
then  is marked as fully visited and the search continues from
is marked as fully visited and the search continues from  as in standard BFS. Namely, after all the nodes reached from
as in standard BFS. Namely, after all the nodes reached from  by an arc, incoming or outgoing, are included in the queue we dequeue
by an arc, incoming or outgoing, are included in the queue we dequeue  and do not consider it again in the search (as suggested by its name).
and do not consider it again in the search (as suggested by its name).
• If a completed node  is reached from its parent-node
is reached from its parent-node 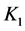 in the queue through an outgoing arc
in the queue through an outgoing arc  then
then  is marked as partially visited. At this point, a node
is marked as partially visited. At this point, a node  can be considered a child of
can be considered a child of  and included in the queue only if it is reached from
and included in the queue only if it is reached from  through an outgoing arc
through an outgoing arc . But
. But  is not dequeued yet; we allow to visit it again. If at some point in the search it is visited from a node
is not dequeued yet; we allow to visit it again. If at some point in the search it is visited from a node  through an incoming arc
through an incoming arc  then
then 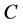 becomes fully-visited and the search from it is continued as in standard BFS described above.
becomes fully-visited and the search from it is continued as in standard BFS described above.
We quit the search when 1) either another incomplete node  is found; in this case the output is a valid path connecting
is found; in this case the output is a valid path connecting  and
and ;
;
2) or no other incomplete node is found and there are only partially visited nodes left in the queue; in this case  is not connected to another incomplete node by a valid path.
is not connected to another incomplete node by a valid path.
4.2. Optimality of the Algorithm Output
We claim that algorithm 4.1 returns an optimal solution for the original problem (IP), based on the following result.
Theorem 3 If there is no valid path connecting any two incomplete task-nodes then the number of completed tasks cannot be increased. Thus, Algorithm 4.1 returns an optimal solution for the paired assignment problem.
Proof: The proof is by induction on the number of task-nodes.
Basis step. The theorem statement is clearly true for any graph with only one task-node.
Inductive step.
Inductive hypothesis. Assume that the theorem statement is true for any graph with less than  task-nodes. That is, for any graph with less than
task-nodes. That is, for any graph with less than  task-nodes, if
task-nodes, if
• assignment 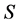 represents an optimal solution of (LP)• there is no valid path connecting any two incomplete task-nodes in
represents an optimal solution of (LP)• there is no valid path connecting any two incomplete task-nodes in then
then  has maximum possible number of completed tasks.
has maximum possible number of completed tasks.
We need to prove the same for any graph with  task-nodes. Suppose an instance of the problem is given by a graph
task-nodes. Suppose an instance of the problem is given by a graph  with
with  task-nodes. Let
task-nodes. Let  be a solution for
be a solution for • corresponding to an optimal solution of (LP)• and with no valid paths connecting incomplete nodes.
• corresponding to an optimal solution of (LP)• and with no valid paths connecting incomplete nodes.
Let  be a different solution that is obtained by reassigning some agents. Let the number of completed tasks in
be a different solution that is obtained by reassigning some agents. Let the number of completed tasks in  be
be . We need to prove that the number of completed tasks is no more than
. We need to prove that the number of completed tasks is no more than  in
in .
.
If none of incomplete and unassigned tasks in  becomes completed in
becomes completed in  then the number of completed tasks clearly cannot be increased. So we need to consider the following two cases.
then the number of completed tasks clearly cannot be increased. So we need to consider the following two cases.
1) An incomplete node in  becomes completed in
becomes completed in .
.
2) An unassigned node in  becomes completed in
becomes completed in .
.
Case 1: Node i is incomplete in S1 and becomes completed in S2.
Get a reduced graph  from
from 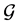 by deleting task-node
by deleting task-node  and the two agent-nodes
and the two agent-nodes  and
and  assigned to
assigned to  in
in . Denote the reduction of
. Denote the reduction of  in
in  by
by , and the reduction of
, and the reduction of  in
in  by
by .
.
Let  be the node from which
be the node from which 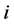 is getting its second assignment in
is getting its second assignment in . Namely, suppose task-node
. Namely, suppose task-node  was assigned to
was assigned to  in
in  and is reassigned to
and is reassigned to  in
in  (see Figure 7). Note that
(see Figure 7). Note that  cannot be an incomplete node in
cannot be an incomplete node in ; otherwise
; otherwise  would be a valid path connecting incomplete nodes
would be a valid path connecting incomplete nodes  and
and  in
in . Thus,
. Thus,  is a completed node in
is a completed node in , and becomes incomplete in
, and becomes incomplete in .
.
We can state the following about .
.
1) The number of completed tasks in 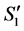 is
is  since it was
since it was 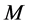 in
in  and
and  was completed in
was completed in  but incomplete in
but incomplete in .
.
2)  is an optimal solution to the linear program for the reduced graph
is an optimal solution to the linear program for the reduced graph  based on the following reason. We cannot have another assignment
based on the following reason. We cannot have another assignment  with larger LP-value for
with larger LP-value for ; otherwise, by adding
; otherwise, by adding  and
and 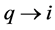 to
to , we could get an assignment with larger LP-value for original
, we could get an assignment with larger LP-value for original .
.
3) We cannot have 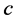 connected to an incomplete node
connected to an incomplete node  in
in  by a valid path
by a valid path ; otherwise
; otherwise  would be a valid path connecting incomplete nodes
would be a valid path connecting incomplete nodes  and
and 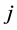 in
in . Thus, there are no valid paths connecting two incomplete task-nodes in
. Thus, there are no valid paths connecting two incomplete task-nodes in  since we didn't have any in
since we didn't have any in  and
and  is the only new incomplete task in
is the only new incomplete task in  compared to
compared to .
.
Based on (2) and (3), the conditions for inductive hypothesis hold for . Thus, we can claim that the number of completed tasks cannot be increased in the result of reassignment from
. Thus, we can claim that the number of completed tasks cannot be increased in the result of reassignment from  to
to . Then, based on (1), the number of completed tasks in
. Then, based on (1), the number of completed tasks in  is at most
is at most , and the number of completed tasks in
, and the number of completed tasks in  is at most
is at most  when we add
when we add  to the completed tasks of
to the completed tasks of .
.
Case 2: Node u is unassigned in S1 and becomes completed in S2.
Get a reduced graph  from
from  by deleting task-node
by deleting task-node  and the two agent-nodes
and the two agent-nodes  and
and  assigned to
assigned to  in
in . Denote the reduction of
. Denote the reduction of  in
in  by
by , and the reduction of
, and the reduction of  in
in  by
by .
.
Let  and
and  be the nodes from which
be the nodes from which  is getting its assignments in
is getting its assignments in . Note that
. Note that  and
and  cannot be both incomplete in
cannot be both incomplete in ; otherwise we would have a valid path between
; otherwise we would have a valid path between  and
and  through the unassigned node
through the unassigned node  (Figure 8). Then we might have the following two subcases.
(Figure 8). Then we might have the following two subcases.
Subcase 2.1: c is completed and d is incomplete in S1.
Then, after deleting agent-nodes  and
and  with their assignments to
with their assignments to  and
and ,
,  becomes incomplete and
becomes incomplete and  becomes unassigned in
becomes unassigned in .
.
We can state the following about .
.
1) The number of completed tasks in  is
is  since it was
since it was  in
in  and
and  was completed in
was completed in  but incomplete in
but incomplete in .
.
2)  is an optimal solution to the linear program for the reduced graph
is an optimal solution to the linear program for the reduced graph  based on the following reason. We cannot have another assignment
based on the following reason. We cannot have another assignment  with larger LP-value for
with larger LP-value for ; otherwise, by adding
; otherwise, by adding  and
and  to
to , we could get an assignment with larger LP-value for original
, we could get an assignment with larger LP-value for original .
.
3) We cannot have  connected to an incomplete node
connected to an incomplete node  by a valid path
by a valid path  in
in ; otherwise
; otherwise  would be a valid path connecting incomplete nodes
would be a valid path connecting incomplete nodes  and
and  in
in  (see Figure 8). We also cannot have two incomplete nodes
(see Figure 8). We also cannot have two incomplete nodes  and
and  connected by a valid path
connected by a valid path  that has
that has  as an interior unassigned node in
as an interior unassigned node in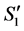 ; otherwise
; otherwise  would be a valid path connecting incomplete nodes
would be a valid path connecting incomplete nodes  and
and  in
in  (Figure 8). Thus, there are no valid paths connecting two incomplete nodes in
(Figure 8). Thus, there are no valid paths connecting two incomplete nodes in .
.
Based on (2) and (3), the conditions for inductive hypothesis hold for , and we can claim that the number of completed tasks cannot be increased in the result of reassignment from
, and we can claim that the number of completed tasks cannot be increased in the result of reassignment from  to
to . Then, based on (1), the number of completed tasks in
. Then, based on (1), the number of completed tasks in  is at most
is at most . Hence the number of completed tasks in
. Hence the number of completed tasks in  is at most
is at most  when we add
when we add  to the completed tasks of
to the completed tasks of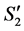 .
.
Subcase 2.2: Both c and d are completed in S1.
Then, after deleting agent-nodes  and
and  with their assignments to
with their assignments to  and
and , both
, both  and
and  become incomplete in
become incomplete in .
.
We can state the following about .
.
1') The number of completed tasks in 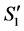 is
is .
.
2')  is an optimal solution to the linear program for the reduced graph
is an optimal solution to the linear program for the reduced graph  based on the following reason. We cannot have another assignment
based on the following reason. We cannot have another assignment  with larger LP-value for
with larger LP-value for ; otherwise, by adding
; otherwise, by adding  and
and  to
to , we could get an assignment with larger LP-value for original
, we could get an assignment with larger LP-value for original .
.
3') We cannot have both  and
and  connected to two different incomplete nodes
connected to two different incomplete nodes  and
and  in
in  by valid paths
by valid paths  and
and ; otherwise
; otherwise  would be a valid path connecting incomplete nodes
would be a valid path connecting incomplete nodes 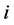 and
and  in
in . But we might have one of
. But we might have one of  and
and  connected to an incomplete node in
connected to an incomplete node in  by a valid path, or
by a valid path, or  and
and  connected to each other by a valid path in
connected to each other by a valid path in .
.
Based on (3'), further division into cases is needed.
Subcase 2.2.1: Suppose none of  and
and  is connected to an incomplete node in
is connected to an incomplete node in  by a valid path. Then there are no valid paths connecting two incomplete nodes in
by a valid path. Then there are no valid paths connecting two incomplete nodes in , and based on (2'), the conditions for inductive hypothesis hold for
, and based on (2'), the conditions for inductive hypothesis hold for . Hence the number of completed tasks cannot be increased in the result of reassignment from
. Hence the number of completed tasks cannot be increased in the result of reassignment from  to
to . Then, based on (1'), the number of completed tasks in
. Then, based on (1'), the number of completed tasks in  is at most
is at most . Thus, the number of completed tasks in
. Thus, the number of completed tasks in 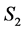 is at most
is at most 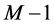 when we add
when we add  to the completed tasks of
to the completed tasks of .
.
Subcase 2.2.2: Suppose  is connected to an incomplete node in
is connected to an incomplete node in  by a valid path (that incomplete node could be
by a valid path (that incomplete node could be  itself). Then after recoloring all the arcs on the path the number of completed tasks will increase by 1. Let
itself). Then after recoloring all the arcs on the path the number of completed tasks will increase by 1. Let  be the solution obtained from
be the solution obtained from  by recoloring the arcs on the valid path.
by recoloring the arcs on the valid path.
We can state the following about .
.
1'') The number of completed tasks in  is
is 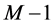 since it has one more completed task than
since it has one more completed task than .
.
2'')  is an optimal solution to the linear program for the reduced graph
is an optimal solution to the linear program for the reduced graph  since it is obtained from
since it is obtained from 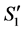 by recoloring the arcs on a valid path which is not changing the LP-value.
by recoloring the arcs on a valid path which is not changing the LP-value.
3'') There are no more valid paths joining two incomplete nodes in .
.
Based on (2'') and (3''), the conditions for inductive hypothesis hold for , and we can claim that the number of completed tasks cannot be increased in the result of reassignment from
, and we can claim that the number of completed tasks cannot be increased in the result of reassignment from  to
to . Then, based on (1''), the number of completed tasks in
. Then, based on (1''), the number of completed tasks in 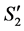 is at most
is at most . Hence the number of completed tasks in
. Hence the number of completed tasks in  is at most
is at most  when we add
when we add  to the completed tasks of
to the completed tasks of .
.
Thus, we proved that the number of completed tasks cannot be increased in any of the above cases. This completes the proof of Theorem 3. ,
5. Future Directions
Below are some possible future directions.
It would make sense to consider the weighted version of the problem. Weights could be associated with the arcs (to make it a variation of the assignment problem) or/and with the nodes.
It is interesting whether there is a purely combinatorial algorithm for solving the problem (without using linear programming).
A generalization of the paired assignemnt problem could be the following: task  can be done only if at least
can be done only if at least  agents are assigned to it.
agents are assigned to it.
• The special case when  for every task
for every task  is the classic maximum matching problem.
is the classic maximum matching problem.
• Our problem is the special case when  for every task
for every task .
.
• The problem for general  might be hard to solve.
might be hard to solve.