Combined Effects of Centrifugal and Coriolis Instability of the Flow through a Rotating Curved Duct with Rectangular Cross Section ()

1. Introduction
Recently, great attention has been paid for the study of flows and heat transfer through rotating curved ducts and channels because of its practical application in chemical, mechanical, bio-mechanical and biological engineering. A quantitative analogy between flows in stationary curved pipes and orthogonally rotating straight pipes has been reported by Ishigaki [1] [2] . Taking this analogy as a basis, this study describes the characteristics of more general and complicated flow in rotating curved ducts. Such rotating flow passages are used in cooling systems in rotating machinery such as in gas turbines, turbo-machinery, electric generators and electric motors. The readers can refer to Berger et al. [3] and Nandakumar and Masliyah [4] for some outstanding reviews on curved duct flows.
One of the interesting phenomena of the flow through a curved duct is the bifurcation of the flow because generally there exist many steady solutions due to channel curvature. An early complete bifurcation study of two-dimensional (2-D) flow through a curved duct with square cross section was performed by Winters [5] . However, an extensive treatment of the flow through a curved square duct was reported by Mondal et al. [6] . He found a close relationship between the unsteady solutions and the bifurcation diagram of steady solutions. Ishigaki [2] examined the flow structure and friction factor numerically for both the counter-rotating and co-rotating curved circular pipe with a small curvature. Selmi et al. [7] examined the combined effects of system rotation and curvature on the bifurcation structure of two-dimensional flows in a rotating curved square duct. Selmi and Nandakumer [8] performed studies on the flow in rotating curved rectangular ducts. Yamamoto et al. [9] employed spectral method to examine the flow structure and the flow rate ratio in a rotating curved square duct flow and found six-cell phenomenon of the secondary flow. Recently, Mondal et al. [10] performed a comprehensive numerical study on the bifurcation structure and the stability of solutions for laminar forced convection in a rotating curved duct of square cross section, and revealed some new features on fluid flow. However, the complete flow structures under the combined action of coriolis and centrifugal instability are still unrevealed for the rotating curved rectangular duct flow at high rotation. It is an attempt of the present study.
It is well known that, fluid flowing in a rotating curved duct is subjected to two forces: the Coriolis force, caused by the rotation of the duct, and centrifugal force caused by the curvature of the duct. These two forces affect each other, as a result complex behavior of the secondary flow and the axial flow can be obtained (Wang and Cheng [11] ). For isothermal flows of a constant property fluid, however, the Coriolis force tends to produce vorticity while centrifugal force is purely hydrostatic (Zhang et al. [12] ). When a temperature induced variation of fluid density occurs for non-isothermal flows, both Coriolis and centrifugal type buoyancy forces can contribute to the generation of vorticity (Mondal et. al., [13] ). These two effects of rotation either enhance or counteract each other in a non-linear manner depending on the direction of wall heat flux and the flow domain. Therefore, the effect of rotation of the system is more subtle and complicated and yields new; richer features of flow and heat transfer in general, bifurcation and stability in particular, for non-isothermal flows. Mondal et al. [13] ] performed numerical prediction of the non-isothermal flows through a rotating curved square duct and revealed some of such new features. Very recently, Mondal et al. [14] investigated the combined effects of the Coriolis force and the centrifugal force on the flows in a rotating curved square duct numerically. The secondary flow characteristics in a curved square duct were investigated experimentally by using visualization method by Yamamoto et al. [15] . Three-dimensional incompressible viscous flow and heat transfer in a rotating U-shaped square duct were studied numerically by Nobari et al. [16] . However, there is no known study on bifurcation and unsteady flow characteristics in a rotating curved rectangular duct with large rotational speed. The present paper is, therefore, an attempt to fill up this gap.
Time dependent analysis of fully developed curved duct flows was first initiated by Yanase and Nishiyama [17] for a rectangular cross section. In that study, they investigated unsteady solutions for the case where dual solutions exist. However, time-dependent behavior of the flow in a curved rectangular duct over a wide range of aspect ratios was investigated, in detail, by Yanase et al. [18] numerically. They observed that periodic oscillations are available with symmetry condition while aperiodic time evolutions without symmetric condition. Wang and Yang [19] [20] performed numerical as well as experimental investigation on fully developed periodic oscillation in a curved square duct. Flow visualization in the range of Dean numbers from 50 to 500 was carried out in their experiment. They showed, both experimentally and numerically, that the temporal oscillation takes place between symmetric/asymmetric 2-cell and 4-cell flows where there are no stable steady flows. Applying spectral method, Yanase et al. [21] performed comprehensive numerical study of the time-dependent solutions for the non-isothermal flows through a curved rectangular duct, and studied the effects of secondary flows on convective heat transfer. In order to study the time-dependent behavior of the unsteady solutions, recently, Mondal et al. [22] performed numerical prediction of the unsteady solutions through curved square duct for isothermal flow. They showed that periodic solutions turn into chaotic solution through a multi-periodic solution, if the Dean number is increased no matter what the curvature is. However, transient behavior of the unsteady solutions, such as periodic, multi-periodic or chaotic solutions, is yet unresolved for the flow through a rotating curved rectangular duct at large pressure gradient with large rotational speed. This motivated the present study to investigate the non-linear behavior of the unsteady solutions by time-evolution calculation.
In the present study, a comprehensive numerical result is presented for fully developed bifurcation structure of two-dimensional (2D) viscous incompressible fluid flow through a rotating curved rectangular duct. Flow characteristics are investigated over a wide range of Taylor number 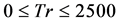 for the Dean number Dn = 2000. Studying the effects of rotation on the flow characteristics, caused by the combined action of centrifugal force and Coriolis force, is an important objective of the present study.
for the Dean number Dn = 2000. Studying the effects of rotation on the flow characteristics, caused by the combined action of centrifugal force and Coriolis force, is an important objective of the present study.
2. Governing Equations
Consider that the flow is viscous and incompressible which is streaming through a rotating curved duct with rectangular cross section. Let 2h and 2l be the height and the width of the cross section. Figure 1 shows the coordinate system, where C is the center of the duct crosssection and L is the radius of curvature of the duct. The 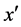 and
and  axes are taken to be in the horizontal and vertical directions respectively, and
axes are taken to be in the horizontal and vertical directions respectively, and 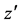 is the coordinate along the center-line of the duct, i.e., the axial direction. The system rotates at a constant angular velocity
is the coordinate along the center-line of the duct, i.e., the axial direction. The system rotates at a constant angular velocity 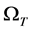 around the
around the 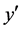 axis. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient
axis. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient  along the center-line of the duct, i.e. the main flow direction. Then the continuity equation and the Navier-Stokes equation, in terms of dimensional variables, are expressed as Continuity equation
along the center-line of the duct, i.e. the main flow direction. Then the continuity equation and the Navier-Stokes equation, in terms of dimensional variables, are expressed as Continuity equation
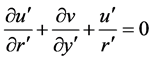 (1)
(1)
Momentum equations
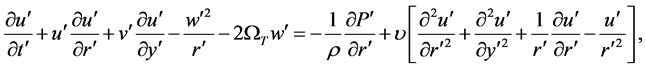 (2)
(2)
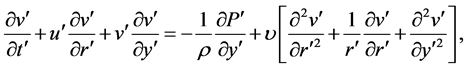 (3)
(3)
 (4)
(4)
where , and
, and 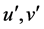 and
and 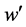 are the dimensional velocity components in the
are the dimensional velocity components in the  and
and 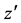 directions respectively. In Equations (1) to (4) the variables with prime denote the dimensional quantities. To nondimensionalize the equations, we use the non-dimensional variables defined as
directions respectively. In Equations (1) to (4) the variables with prime denote the dimensional quantities. To nondimensionalize the equations, we use the non-dimensional variables defined as
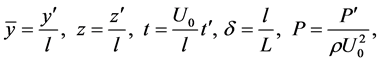
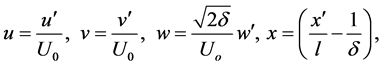
where 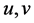 and
and 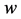 are the non-dimensional velocity components in the
are the non-dimensional velocity components in the  and
and  directions, respectively; t is the non-dimensional time, P is the non-dimensional pressure,
directions, respectively; t is the non-dimensional time, P is the non-dimensional pressure, is the non-dimensional curvature defined as
is the non-dimensional curvature defined as
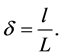 The sectional stream function
The sectional stream function 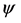 is introduced as
is introduced as
 (5)
(5)