1. Introduction
A graph invariant is any function on a graph that does not depend on a labeling of its vertices. Topological indices and graph invariants based on the distances between the vertices of a graph are widely used in theoretical chemistry to establish relations between the structures and the properties of molecules. Topological indices provide correlations with physical, chemical and thermodynamic parameters of chemical compounds [2]. In this paper, we only consider simple and connected graphs. Let G be a graph on n vertices and 
edges. We denote the vertex and the edge set of G by 
and
, respectively. As usual, the distance between the vertices 
and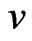 
of G, denoted by 
(
for short), is defined as the length of a minimum path connecting them. We let 
be the degree of a vertex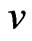 
in G. The eccentricity, denoted by
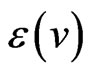, is defined as the maximum distance from vertex 
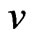to any other vertex. The diameter of a graph G, denoted by
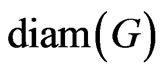, is the maximum eccentricity over all vertices in a graph G.
The Cartesian product 
of graphs G and H is a graph such that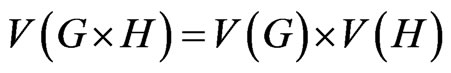
, and any two vertices 
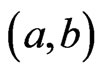and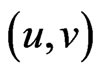 
are adjacent in 
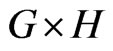if and only if either 
and 
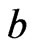is adjacent to
, or 
and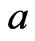 
is adjacent to
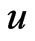, see [3] for details. Let 
and 
be two graphs with disjoint vertex sets 
and 
and edge sets 
and
. The join 
is the graph union 
together with all the edges joining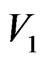 
and
. The composition 
is the graph with vertex set 
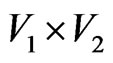and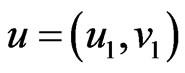 
is adjacent to 
whenever (
is adjacent with
) or (
and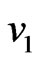 
is adjacent to
), [3, p. 185]. The disjunction 
of graphs 
and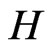 
is the graph with vertex set 
and 
is adjacent to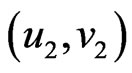 
whenever 
or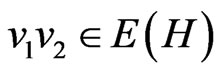
. The symmetric difference 
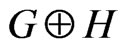of two graphs 
and 
is the graph with vertex set 
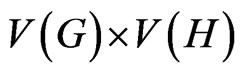and
.
The first Zagreb index was originally defined as
[4]. The first Zagreb index can be also expressed as a sum over edges of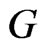
,
We refer readers to [5]
for the proof of this fact and for more information on Zagreb index. The first Zagreb coindex of a graph 
is defined in [6] as:
Let 
be the number of pairs of vertices of a graph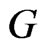 
that are at distance
, 
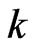be a real numberand
, that is called the Wienertype invariant of 
associated to
, see [7,8] for details. Additively weighted Harary index is defined in [9] as
Dobrynin and Kochetova in [10] and Gutman in [11] introduced a new graph invariant with the name degree distance that is defined as follows:
In [12], the modified degree distance was defined as follows:
The generalized degree distance, denoted by
, is defined as follows in [1].
For every vertex 
and real number
, 
is defined by
, where
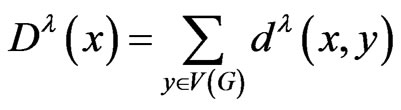. We then define
If
, then
. When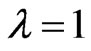
, this new topological index 
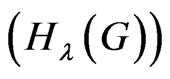is equal to the degree distance (or Schultz index). There are many papers for studying this topological index, for example see [13-16]. Also if
, then 
Therefore the study of this new topological index is important and we try to obtain some new results related to this topological index. The modified generalized degree distance, denoted by
, is defined in [1] as:
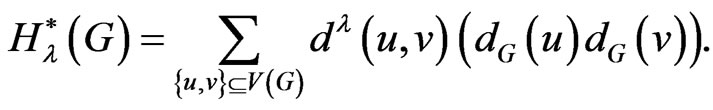
If
, then
.
We construct graph polynomials having the property such that their first derivatives at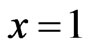 
are equal to the generalized degree distance, the modified generalized degree distance and Wiener-type invariant respectively. These polynomials are defined as follows:
and
The Wiener index of the Cartesian product of graphs was studied in [17,18]. In [19], Klavžar, Rajapakse and Gutman computed the Szeged index of the Cartesian product of graphs. In [9,20-24], exact formulae for the hyper-Wiener, the first Zagreb index, the second Zagreb index and Schultz polynomials of some graph operations were computed.
Throughout this paper, 
and 
denote the cycle, path, complete graph and star on 
vertices. The complement of a graph 
is a graph 
on the same vertices such that two vertices of 
are adjacent if and only if they are not adjacent in
. The graph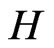 
is usually denoted by
. Our other notations are standard and taken mainly from [2,25,26].
In this paper we present explicit formulas for 
of graph operations containing the Cartesian product, composition, join, disjunction and symmetric difference of graphs and introduce generalized and modified generalized degree distance polynomials of graphs, such that their first derivatives at 
are respectively, equal to the generalized degree distance and the modified generalized degree distance. These polynomials are related with Wiener-type invariant polynomial of graphs.
2. Main Results
The aim of this section is to compute the generalized degree distance for five graph operations. We start with a lemma which gives some information about the number of vertices and edges of operations on two arbitrary graphs. For a given graph
, the number of vertices and edges will be denoted by 
and
, respectively.
Lemma 2.1. [3,20] Let 
and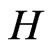 
be graphs. Then we have:
a)
and
b) The graph 
is connected if and only if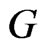 
and 
are connected.
c) If 
and 
are vertices of
, then
.
d) The Cartesian product, join, composition, disjunction and symmetric difference of graphs are associative and all of them are commutative except the composition of graphs.
e)
.
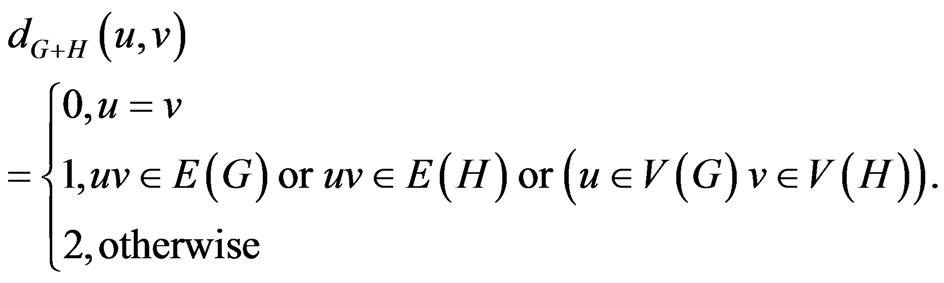f)
g)
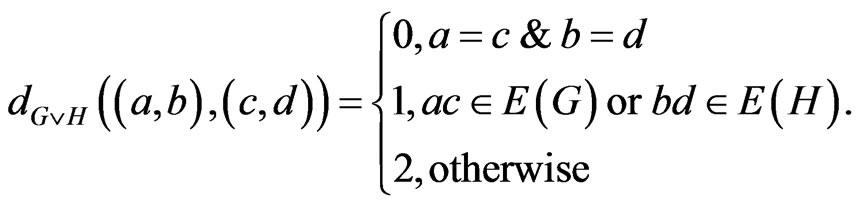
h)
i) 
j) 
k) 
l)
m)
In Theorem 2.2, we give a formula for the generalized degree distance of the join of two graphs.
Theorem 2.2. Let 
and 
be two graphs. Then
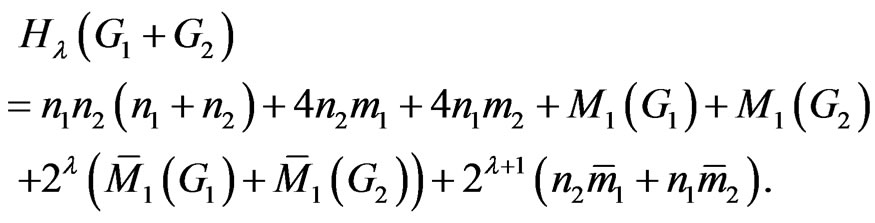
Proof. It is obvious from definition that for any
, the distance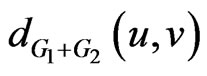 
is either 1 or 2. In the formula for
, we partition the set of pairs of vertices of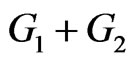 
into three subsets 
and
. In 
we collect all pairs of vertices u and v such that u is in 
and v is in
. Hence, they are adjacent in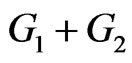
. The set 
is the set of pairs of vertices u and v which are in
. Also we partition the sum in the formula of 
into three sums 
so that 
is over 
for
. For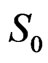 
we obtain
and
Similarly,
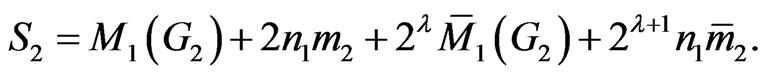
Therefore
□
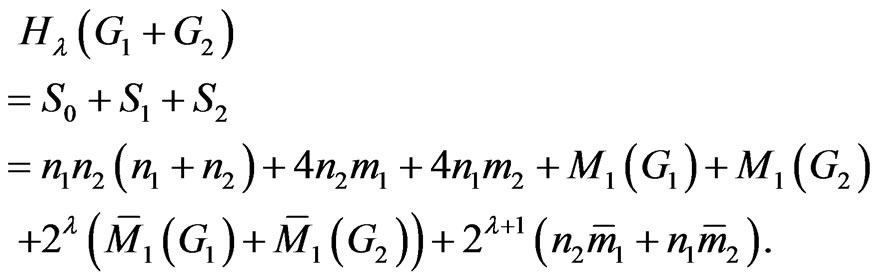Corollary 2.3. Let G be a connected graph with n vertices and m edges. Then
.
The exact formulas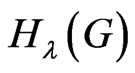 
for the fan graph K1 + Pn and for the wheel graph 
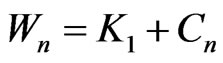are given in the following Corollary.
Corollary 2.4.
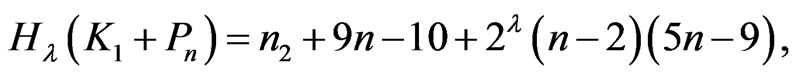
and
Remark 2.5. In the above theorem, if
, then we obtain
, which gives first derivatives formula Theorem 3 in [22] at
.
In the next theorem we obtain the exact formula for the generalized degree distance of the composition of two graphs.
Theorem 2.6. Let 
and 
be two graphs. Then
Proof. Suppose 
and 
are two set of vertices of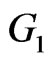 
and
, respectively. Then by Lemma 2.1 and definition of
, we have:
So the proof of theorem is now completed. □
By composing paths and cycles with various small graphs we can obtain classes of polymer-like graphs. Now we give the formula of the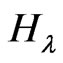 
index for the fence graph 
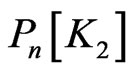and the closed fence
.
Corollary 2.7.
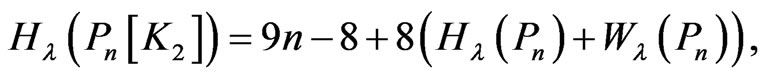
and
Remark 2.8. In Theorem 2.6, if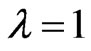
, then we obtain
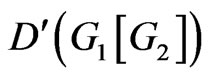, which gives first derivatives formula Theorem 5 in [22] at
.
Now we prove the theorem that characterizes the generalized degree distance of the disjunction of two graphs.
Theorem 2.9. Let 
and 
be two graphs. Then
Proof. According to definition of
, we have the following relations:
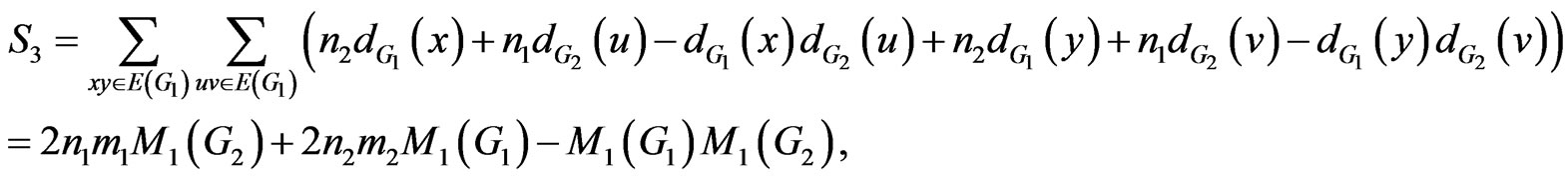
and
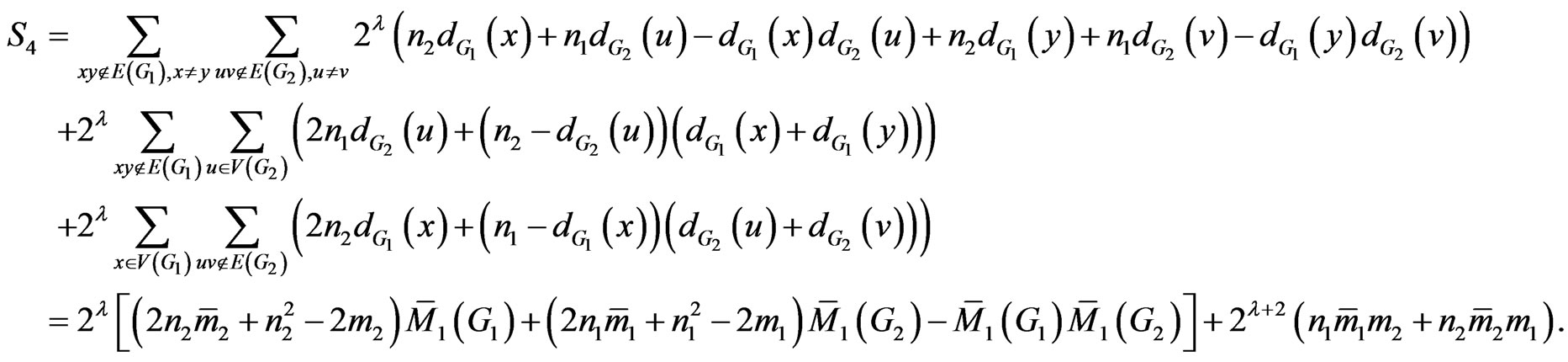
So we have:
This completes the proof. □
Now we prove the theorem that characterizes the generalized degree distance of the symmetric difference of two graphs.
Theorem 2.10. Let G1 and G2 be two graphs. Then
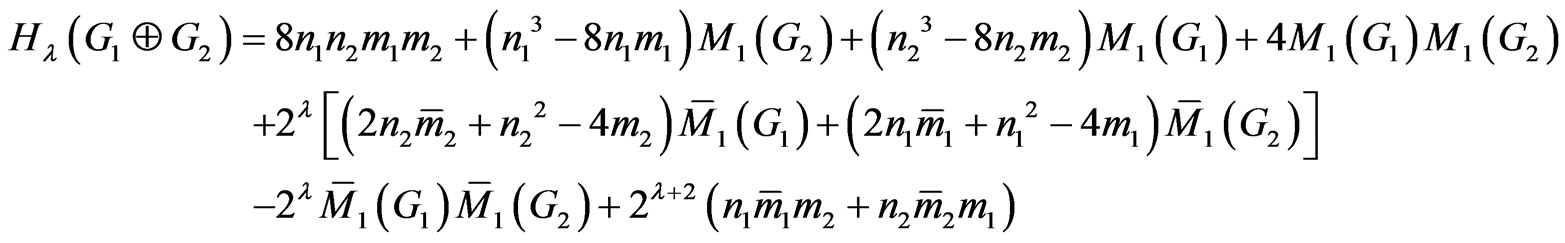
Proof. We consider four sums 
as follows:
similarly to 
and
By the definition of
, we have:
So the proof is now completed. □
In the next theorem we find the generalized degree distance of the Cartesian product of two graphs.
Theorem 2.11. Let 
and 
be two graphs. Then
Proof. Suppose 
and 
are two set of vertices of 
and
, respectively. Then by Lemma 2.1 and definition of
, we have:
So the proof is now completed. □
As an application of the above theorem, we list explicit formulae for the generalized degree distance of 
and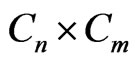
. These graphs are known as the rectangular grid, the 
nanotube, and the 
nanotorus, respectively.
Lemma 2.12. Define
. By [1,23], we have:
Corollary 2.13. By Theorem 2.9 and Lemma 2.12 we have:
and
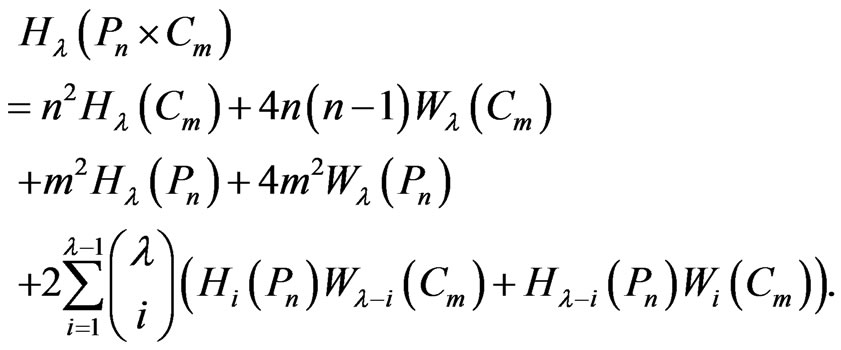
Remark 2.14. In the above theorem, if
, then we obtain
, which gives first derivatives formula Theorem 1 in [22] at
.
Now we obtain the relation between the generalized degree distance polynomial and Wiener-type invariant polynomial and the relation between the modified generalized degree distance polynomial and Wiener-type invariant polynomial for graphs.
Theorem 2.15. If 
is a graph with 
vertices and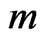 
edges, then
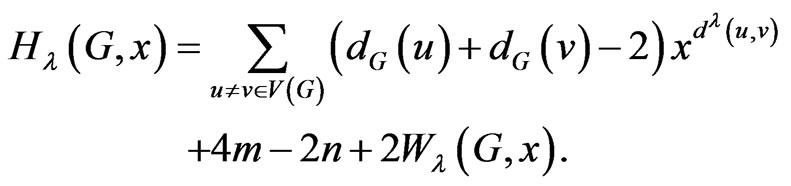
Proof. By definition, we have
This completes the proof. □
Theorem 2.16. If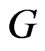 
is a graph with 
vertices and 
edges, then
Proof. By definition, we have
This completes the proof. □
NOTES