1. Introduction
Erdélyi [2] investigated the solutions of integral equations whose kernels contain Legendre functions. Love [3] solved the integral equations involving hypergeometric functions using fractional derivatives. Using variance of fractional integration, Habibullah [4] investigated the solution of the integral equations involving confluent hypergeometric functions and Srivastava [5] discussed the equations with polynomial kernels.
Diaz et al. [6-8] have introduced k-gamma and k-beta functions and proved a number of their properties that we are interested in. They have also studied k-zeta function and k-hypergeometric function based on Pochhammer k-symbols for factorial functions. These studies were then followed by works of Mansour [9], Kokologiannaki [10], Krasniqi [11,12] and Merovci [13] elaborating and strengthening the scope of k-gamma and k-beta functions. Very recently, Mubeen and Habibullah [14] gave a simple and useful integral representations of generalized khypergeometric and confluent k-hypergeometric functions that could helpful in completing the present research paper.
2. Fractional Integration
Mubeen and Habibullah [1] defined a k-fractional integration as a variant of Riemann-Liouville fractional integral as
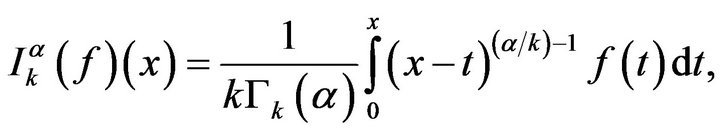
for
. It reduces to the classical Riemann-Liouville fractional integral by taking 
as
.
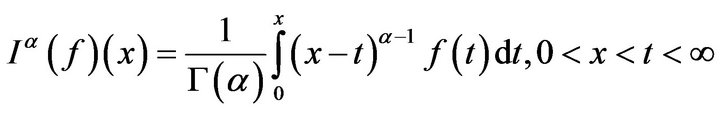3. k-Hypergeometric and Confluent
k-Hypergeometric Differential Equations
The following k-hypergeometric function defined by Mubeen and Habibullah [14]
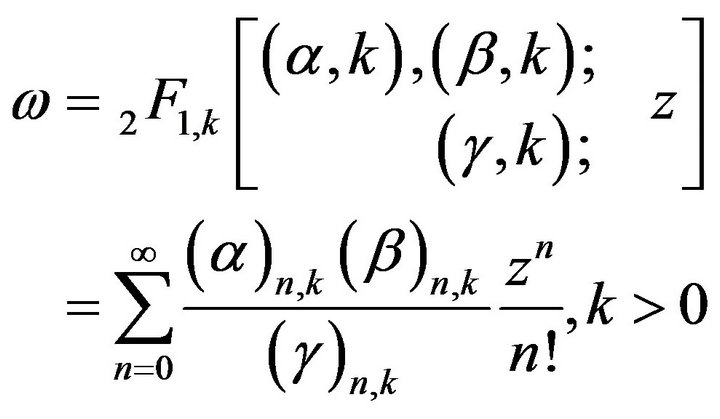
is the solution of the linear second order differential equation of the form
.
In this article, we call it k-hypergeometric differential equation. It reduces to ordinary hypergeometric differential equation by taking
.
And also the following confluent k-hypergeometric function defined by Mubeen and Habibullah [14]
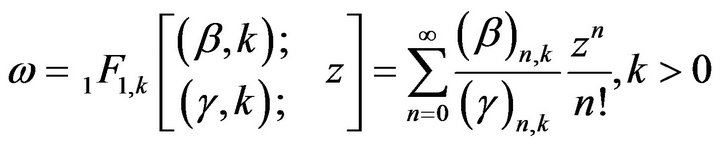is the solution of the linear second order differential equation of the form
.
In this article, we call it confluent k-hypergeometric differential equation. It reduces to ordinary hypergeometric differential equation by taking
.
4. Main Results
Theorem 4.1. If 
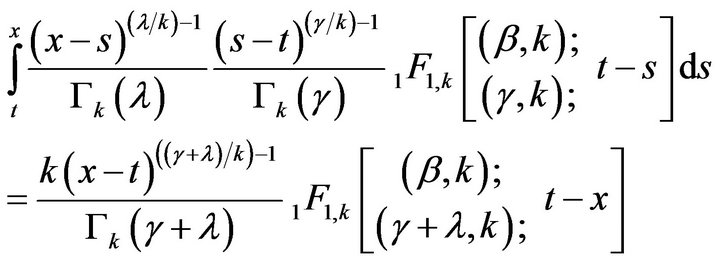
Proof. Consider
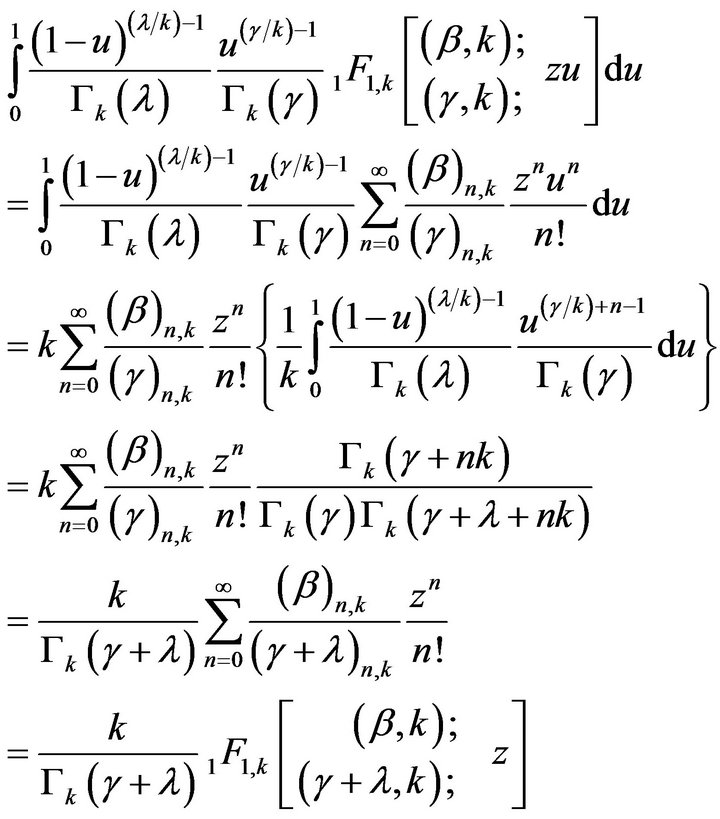
Put 
in the above equation, then we get the desired result.
Theorem 4.2. Let
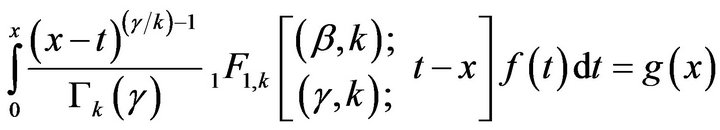
for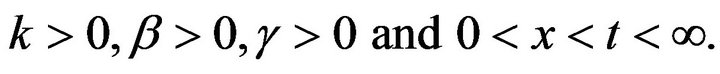 
If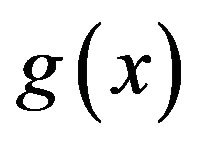 
is a given function, then
.
Proof. Set
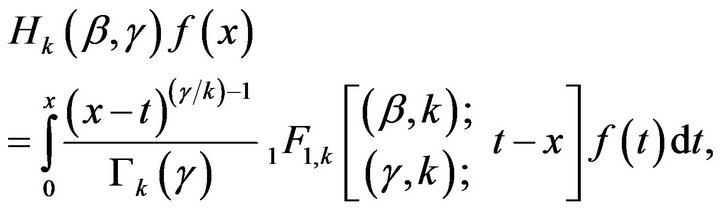
where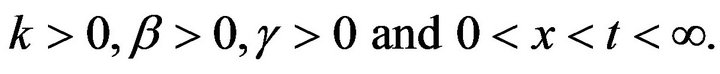 
Apply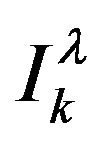 
on both sides, we get the following
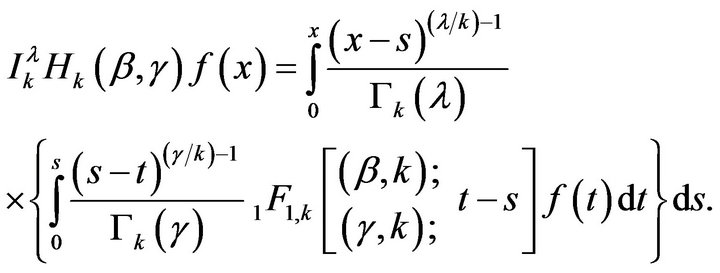
Changing the order of integration by using Fubini’s theorem.
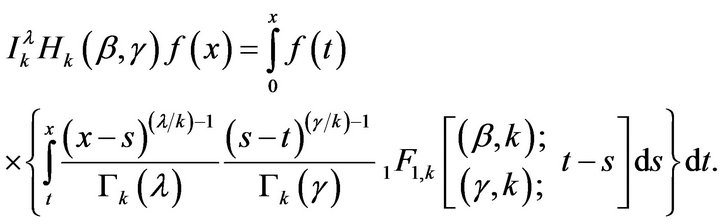
By Theorem 4.1, we have
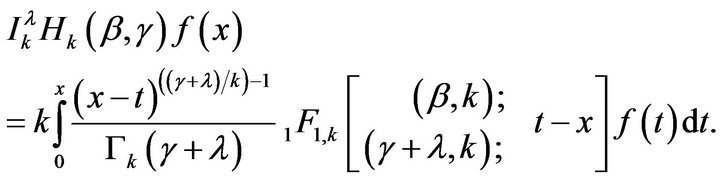
This implies that
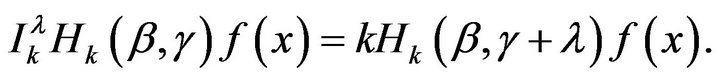
Since
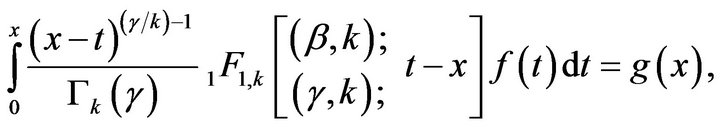
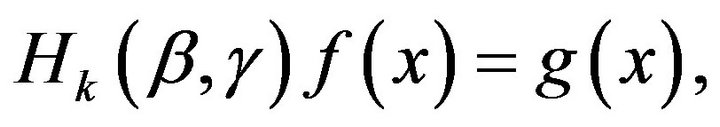
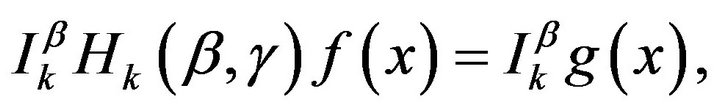
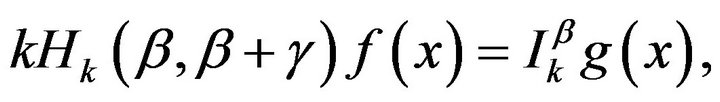
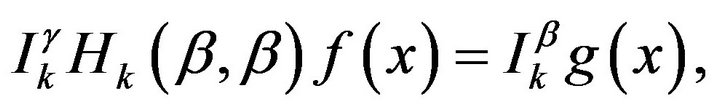
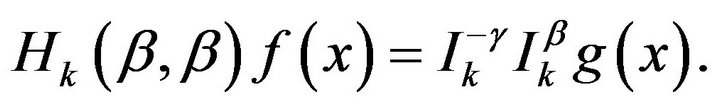
This may be written as
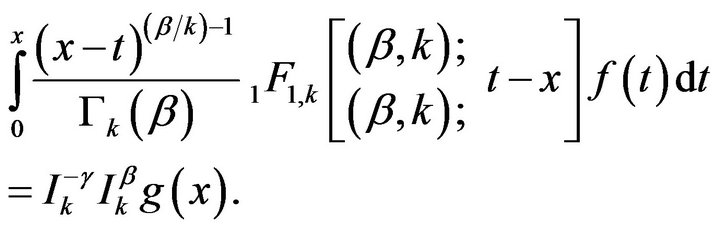
Since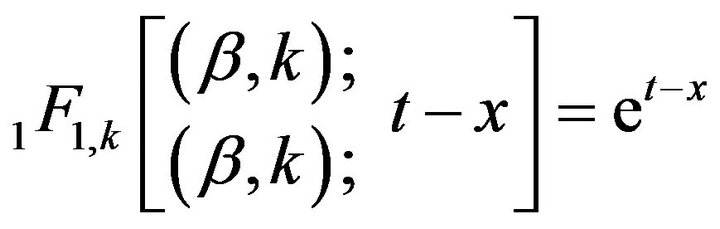
, we obtain
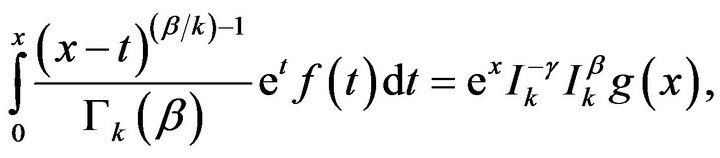
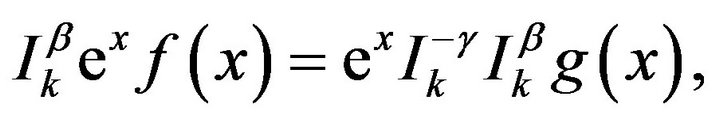
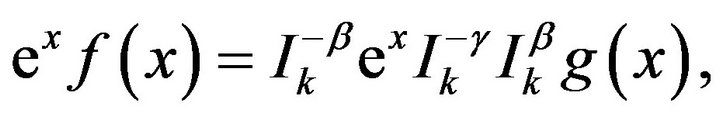
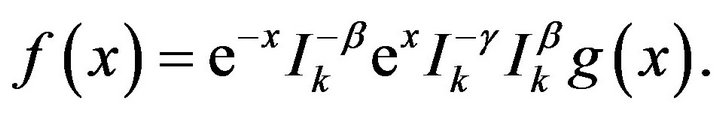
This is the solution of the integral equation, if it exists.
This integral equation implies that
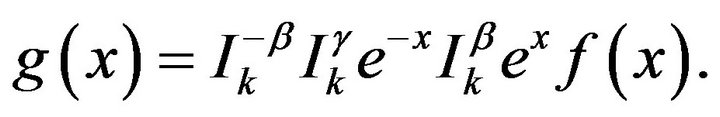
Now, we find a solution of another integral equation
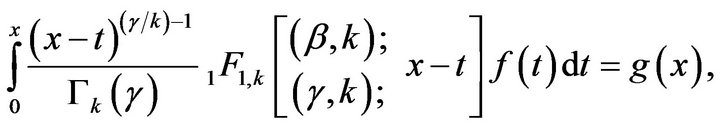
for 
Theorem 4.3. Let
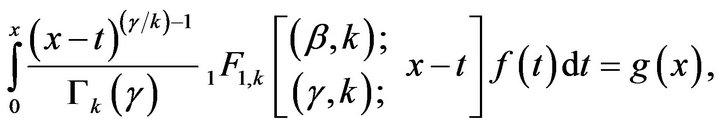
for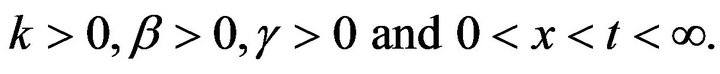 
If 
is a given function, then
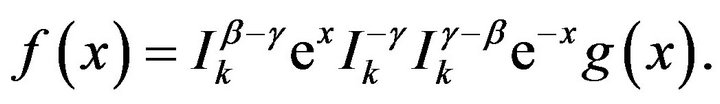
Proof. Consider
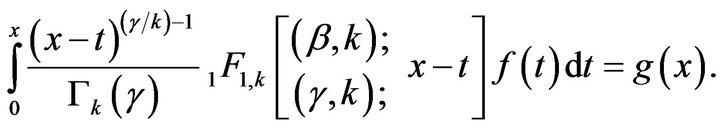
Using the Mubeen’s relation [15]
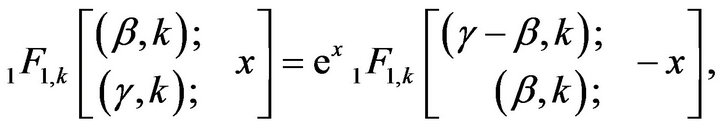
we obtain the following
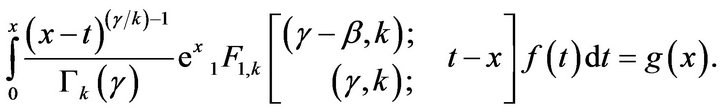
Thus, if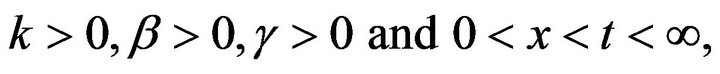 
then
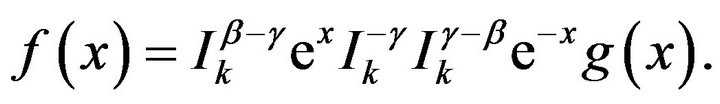
Also, we have the following result
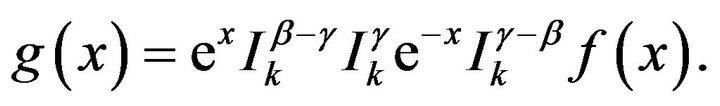
5. Acknowledgements
The author would like to express profound gratitude to referees for deeper review of this paper and their valuable advice and the referee’s useful suggestions that led to an improved presentation of the paper. The author is also pleased to pay special thanks to Dr. Atiq ur Rehman for his support in this research.