1. Introduction
Finite partial orders or posets have numerous applications, including scheduling [1-8], molecular evolution [9-12], data mining [13-17], graph theory [18-23], and algebra [24-27]. Many applications implicitly or explicitly involve linear extensions of posets. For example, the solution of many scheduling problems requires a linearization of the jobs being scheduled consistent with some precedence constraints given by a poset. As the number of linear extensions of a poset may be exponential in the number of elements of the base set, many computational problems related to linear extensions are not solvable in polynomial time. Ruskey [28], West [29], Pruesse and Ruskey [30], Canfield and Williamson [31], Korsh and LaFollette [32], and Ono and Nakano [33] provide algorithms to generate all of the linear extensions of a finite poset. As the size of a solution may be exponentially large, these algorithms emphasize the ability to generate each successive linear extension in polynomial time, at least on average. Sampling the linear extensions of a poset is easier. Bubley and Dyer [34] use a rapidly mixing Markov chain to generate a random linear extension of a finite poset, sampled almost uniformly.
Problems in mining order information from databases of sequences (see, e.g., [16,17,35,36]) have an inverted character from that of many computational problems involving posets. Here, a problem instance is a set of linear orders of items from some universal set, while a solution is one or more posets that well explain, through their linear extensions, a significant number of the linear orders. An example from computational neuroscience [37] might go as follows. Each item is the firing of a neuron, while each linear order is a sequence of neuronal firings, ordered in time from an experiment. The solution is a neural circuit that explains a set of such linear orders. These novel problems are ripe for mathematical formalization and study. In this paper, we define and study one such problem. A problem instance is a set of permutations of a base set, and a solution covers the instance with linear extensions (Section 2). We prove that the Poset Cover problem (a decision problem) is NP-complete in Section 3. In Section 4, we explore how cover relations relate to poset covers. Finally, we develop a polynomial-time algorithm to find a partial cover in Section 5.
2. Preliminaries
In this section, we establish terminology and notation and prove some basic results.
A partial order or poset 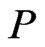 is an irreflexive, antisymmetric, and transitive binary relation
is an irreflexive, antisymmetric, and transitive binary relation  defined on a finite set
defined on a finite set  of cardinality
of cardinality . We write
. We write  as the ordered pair
as the ordered pair . Equivalently, poset
. Equivalently, poset  is a transitive directed acyclic graph (DAG), namely,
is a transitive directed acyclic graph (DAG), namely,
 . If G is a DAG, then its transitive closure is a poset by this equivalence. The rank function
. If G is a DAG, then its transitive closure is a poset by this equivalence. The rank function 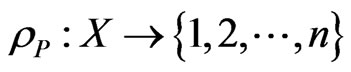 is given by
is given by
 . The empty poset is
. The empty poset is .
.
Let  be distinct. Then
be distinct. Then 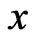 and
and  are comparable in
are comparable in , written
, written , if
, if  or
or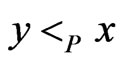 , while x and
, while x and  are incomparable, written
are incomparable, written , otherwise. Moreover, x is covered by y or y covers x, written
, otherwise. Moreover, x is covered by y or y covers x, written , if
, if  and there is no
and there is no 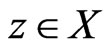 such that
such that . In this case, the ordered pair
. In this case, the ordered pair  is a cover relation for
is a cover relation for . It is well-known that a (finite) poset is uniquely determined by its set of cover relations (see [38]).
. It is well-known that a (finite) poset is uniquely determined by its set of cover relations (see [38]).
If  and
and  are posets on the same set
are posets on the same set , then
, then  is an extension of
is an extension of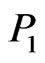 , written
, written , if, for all
, if, for all  implies
implies . The relation
. The relation 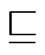 on posets of
on posets of  is reflexive, antisymmetric, and transitive.
is reflexive, antisymmetric, and transitive.
A linear order 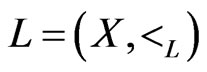 on X is a poset L such that, for
on X is a poset L such that, for , either
, either  or
or  holds. If
holds. If  is a linear order, then the rank function
is a linear order, then the rank function  is a bijection. Setting
is a bijection. Setting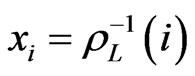 ,
,  can be written as the sequence
can be written as the sequence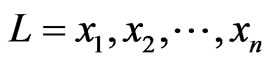 , which is a permutation of
, which is a permutation of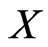 . Also, we write
. Also, we write  for the element of rank
for the element of rank  in
in . A linear extension
. A linear extension  of a poset
of a poset  is a linear order such that
is a linear order such that . The set of all linear extensions of
. The set of all linear extensions of  is
is . Note that
. Note that  is the set of all linear orders on
is the set of all linear orders on . Brightwell and Winkler [39] prove that the problem of determining
. Brightwell and Winkler [39] prove that the problem of determining  for a poset
for a poset  is #P-complete.
is #P-complete.
Let  be a set of
be a set of  posets on
posets on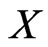 . This set covers the set of linear orders
. This set covers the set of linear orders

A poset 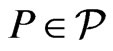 is maximal in
is maximal in  if
if  and there is no poset
and there is no poset  of
of  such that
such that , and
, and . Let
. Let  be a set of posets on
be a set of posets on , and let
, and let 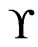 be a set of linear orders on
be a set of linear orders on .
.  blankets
blankets  if
if

Lemma 1 Let  be the set of linear orders that is covered by a set
be the set of linear orders that is covered by a set 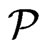 of posets of cardinality
of posets of cardinality . Then, there exists a cover
. Then, there exists a cover  of cardinality
of cardinality 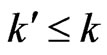 that also covers
that also covers 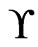 such that every poset in
such that every poset in  is maximal in
is maximal in .
.
Proof. We construct  by examining each poset in
by examining each poset in . Let
. Let . If
. If  is maximal in
is maximal in , then add
, then add  to
to . Otherwise, let
. Otherwise, let  be a poset of minimum cardinality (as a set of ordered pairs) such that
be a poset of minimum cardinality (as a set of ordered pairs) such that  and
and . Since
. Since  is not maximal,
is not maximal, . Moreover, any poset
. Moreover, any poset  contained in
contained in  of smaller cardinality will have
of smaller cardinality will have . Add
. Add  to
to .
.
The constructed  has cardinality
has cardinality . Moreover,
. Moreover, 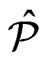 also covers
also covers  and every poset in
and every poset in  is maximal in
is maximal in . The lemma follows.
. The lemma follows.
In this paper, we are interested in reversing the cover relationship by addressing the problem of finding a minimum set of posets that covers a given set of linear orders. As a decision problem, this is Poset Cover INSTANCE: A base set  of cardinality
of cardinality ; a nonempty set
; a nonempty set  of linear orders over
of linear orders over ; and an integer
; and an integer .
.
QUESTION: Is there a set 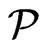 of posets on
of posets on  of cardinality
of cardinality  that covers
that covers ?
?
This problem is shown to be NP-complete in Section 3.
Let  be a linear order on
be a linear order on . For each
. For each  satisfying
satisfying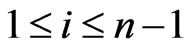 , the i-swap of
, the i-swap of  is the linear order
is the linear order .
.
Let . Evidently,
. Evidently,  , so the
, so the
 -swap relation is symmetric, written
-swap relation is symmetric, written . For pairs
. For pairs  that are
that are  -swaps of each other, for some
-swaps of each other, for some , we define the function
, we define the function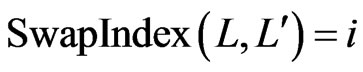 . Note that the set differences of
. Note that the set differences of  and
and , namely
, namely
 and
and , each consist of a single ordered pair. In this case, the swap pair for
, each consist of a single ordered pair. In this case, the swap pair for  and
and  is the unordered pair
is the unordered pair
 ; otherwise,
; otherwise,
 . Two linear orders
. Two linear orders  and
and  differ by a swap, written
differ by a swap, written , if
, if , for some
, for some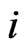 . Since
. Since  if and only if
if and only if , the
, the
 relation is also symmetric. If
relation is also symmetric. If ,
,  and
and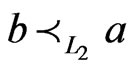 , then we write
, then we write  to mean that
to mean that  for some
for some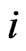 , where the elements swapped are
, where the elements swapped are  and
and .
.
Let  be a set of linear orders on
be a set of linear orders on . The swap graph of
. The swap graph of  is the undirected graph
is the undirected graph
 . An edge
. An edge  of
of
 is labeled
is labeled . Let
. Let  be a poset on
be a poset on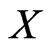 , and let
, and let . Then,
. Then,  is a partial cover of
is a partial cover of  including
including  if
if  and
and . The swap graph is the same as the adjacent transposition graph of Pruesse and Ruskey [30]. The swap graph of
. The swap graph is the same as the adjacent transposition graph of Pruesse and Ruskey [30]. The swap graph of  is bipartite, since every edge connects an even permutation to an odd permutation. Moreover, the swap graph
is bipartite, since every edge connects an even permutation to an odd permutation. Moreover, the swap graph 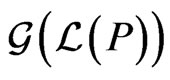 of the linear extensions of a single poset is connected (see [30]).
of the linear extensions of a single poset is connected (see [30]).
Let  be the set of all posets on
be the set of all posets on . Let
. Let  be a set of ordered pairs. The up-set of
be a set of ordered pairs. The up-set of  is
is

 is empty if and only if the directed graph
is empty if and only if the directed graph  contains cycles. Let
contains cycles. Let
 be a set of unordered pairs. The down-set of
be a set of unordered pairs. The down-set of  is
is

 , and we always have the empty poset
, and we always have the empty poset .
.
If , then define the minimal element in
, then define the minimal element in  to be
to be

The following properties of  follow directly from the definitions.
follow directly from the definitions.
Lemma 2 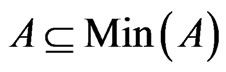 and
and
 .
.
We have the following properties of up-sets and downsets.
Lemma 3 Let . If
. If , then
, then
 . Let
. Let
 . If
. If , then
, then
 .
.
Proof. Suppose that . By the definition of upsets,
. By the definition of upsets,

Now, suppose that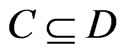 . Then,
. Then,
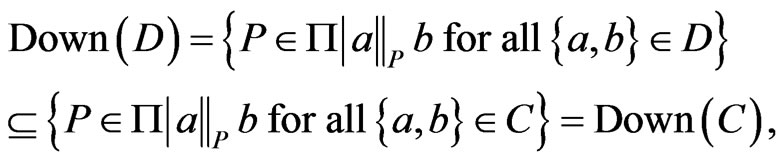
by the definition of down-sets.
3. NP-Completeness of Poset Cover
In this section, we show that PosetCover is NP-complete, in the process using the following known NP-complete decision problem [40].
Cubic Vertex Cover INSTANCE: A nonempty undirected graph  that is cubic, that is, in which every vertex has degree 3; and an integer
that is cubic, that is, in which every vertex has degree 3; and an integer .
.
QUESTION: Is there a subset 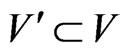 of cardinality
of cardinality  such that every edge in
such that every edge in  is incident on at least one vertex in
is incident on at least one vertex in ?
?
Theorem 4 Poset Cover is NP-complete.
Proof. We show that Poset Cover is in NP and that Cubic Vertex Cover reduces to Poset Cover in polynomial time.
We first show that Poset Cover is in NP. Let ,
,  , and
, and  constitute an instance of Poset Cover, and let
constitute an instance of Poset Cover, and let  be a set of posets on
be a set of posets on . First, it is easy to check whether
. First, it is easy to check whether 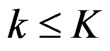 in time polynomial in
in time polynomial in  and
and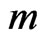 ; if
; if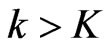 , then return No. Second, if the cardinality check succeeds, check whether
, then return No. Second, if the cardinality check succeeds, check whether 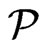 covers
covers  as follows. For each poset
as follows. For each poset  in turn, use the Korsh and LaFollette [32] algorithm to generate all the linear extensions of
in turn, use the Korsh and LaFollette [32] algorithm to generate all the linear extensions of , one at a time, in constant time per linear extension. As each linear extension
, one at a time, in constant time per linear extension. As each linear extension 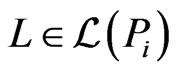 is generated, check whether
is generated, check whether . If not, then return No. If so, then mark that element of
. If not, then return No. If so, then mark that element of 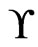 Covered. Note that the number of linear orders generated by a run of the Korsh and LaFollette algorithm before completion or returning No is at most
Covered. Note that the number of linear orders generated by a run of the Korsh and LaFollette algorithm before completion or returning No is at most . Hence, the worst-case time for one run of the algorithm, including the checking, is
. Hence, the worst-case time for one run of the algorithm, including the checking, is . Once all the posets and their linear extensions are processed, check whether every element of
. Once all the posets and their linear extensions are processed, check whether every element of  is marked Covered. If so, then return Yes; otherwise, return No. We find that the worstcase time to check whether
is marked Covered. If so, then return Yes; otherwise, return No. We find that the worstcase time to check whether  covers
covers  is
is  , since
, since . This is polynomial in the size of the original instance. We conclude that Poset Cover is in NP.
. This is polynomial in the size of the original instance. We conclude that Poset Cover is in NP.
Now, let  and
and  constitute an instance of Cubic Vertex Cover . Without loss of generality, assume that
constitute an instance of Cubic Vertex Cover . Without loss of generality, assume that  and that
and that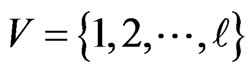 . Let
. Let  , and let
, and let  be an arbitrary labeling of the
be an arbitrary labeling of the  edges of
edges of . As a running example of our reduction, we provide the cubic graph in Figure 1, with
. As a running example of our reduction, we provide the cubic graph in Figure 1, with  vertices and
vertices and  edges. To complete the instance of Cubic Vertex Cover , set
edges. To complete the instance of Cubic Vertex Cover , set .
.
Let , and let
, and let 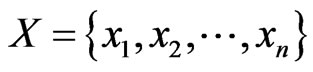 be a base set of
be a base set of  elements. Let
elements. Let , the base order, be the linear order on
, the base order, be the linear order on  specified by
specified by

We view the elements of  as consisting of
as consisting of  adjacent, non-overlapping pairs. Specifically, the pairs are
adjacent, non-overlapping pairs. Specifically, the pairs are  and
and , where
, where . All elements of
. All elements of  are obtained by a small set of swaps of such pairs, applied to
are obtained by a small set of swaps of such pairs, applied to .
.

Figure 1. A cubic graph as part of an instance of cubic vertex cover.
The first s pairs correspond to the s edges in a natural way. In particular, edge  is associated with the edge order
is associated with the edge order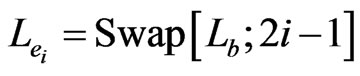 . Continuing the example, we set
. Continuing the example, we set ,
,

and, for example,

For each vertex , there are three edges incident on
, there are three edges incident on ; let the indices of those edges be
; let the indices of those edges be , and
, and . For each pair
. For each pair  and
and  of these edges, we define the pair edge order to be
of these edges, we define the pair edge order to be
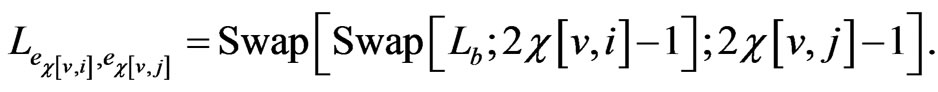
For the running example, there are 18 pair edge orders. For each triple , and
, and , we define the triple edge order to be
, we define the triple edge order to be
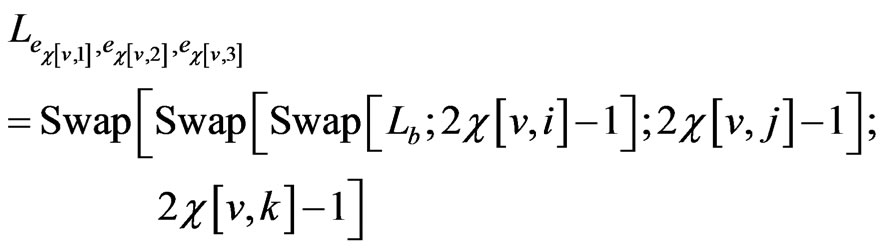
For the running example, there are 6 triple edge orders.
The primary orders are the base, edge, pair edge, and triple edge orders. For primary pair edge order , there is a corresponding secondary pair edge order obtained by swapping
, there is a corresponding secondary pair edge order obtained by swapping  and
and , which is
, which is

For primary triple edge order , there is a corresponding secondary triple edge order obtained by swapping
, there is a corresponding secondary triple edge order obtained by swapping  and
and , which is
, which is

For the running example, there are 18 secondary pair edge orders and 6 secondary triple edge orders.
Collect the various orders into five sets, as follows:

We can now complete our instance of Poset Cover by setting
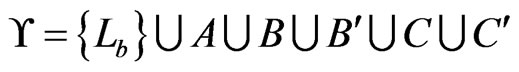
and setting the integer parameter . Note that
. Note that . For the running example,
. For the running example,  and
and .
.
It remains to show that an instance of Cubic Vertex Cover is a Yes instance if and only if the corresponding instance of Poset Cover is a Yes instance.
Fix an instance  and
and  of Cubic Vertex Cover . Let
of Cubic Vertex Cover . Let , and
, and  constitute the corresponding instance of Poset Cover, as constructed above. By Lemma 1, we may assume that every element of a cover
constitute the corresponding instance of Poset Cover, as constructed above. By Lemma 1, we may assume that every element of a cover  of
of  is maximal in
is maximal in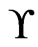 . Since the elements of
. Since the elements of  must be blanketed by any cover, we may assume that the set
must be blanketed by any cover, we may assume that the set

is a subset of . Similarly, since the elements of
. Similarly, since the elements of 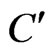 must be blanketed by any cover, we may assume that the set
must be blanketed by any cover, we may assume that the set

is a subset of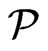 . Note that
. Note that  and that
and that  blankets
blankets .
.
First, assume that  is a vertex cover of
is a vertex cover of  of cardinality at most
of cardinality at most . Define
. Define

Note that  and that, by previous observations, it suffices to demonstrate that
and that, by previous observations, it suffices to demonstrate that  blankets
blankets 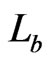 and
and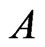 . Since
. Since  is nonempty,
is nonempty, 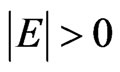 , and
, and . Therefore,
. Therefore,  is blanketed by each of the posets
is blanketed by each of the posets  in
in 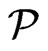 corresponding to a vertex
corresponding to a vertex . For an edge
. For an edge , there is a
, there is a  incident on
incident on . Then,
. Then,  is blanketed by the poset
is blanketed by the poset
 in
in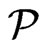 , and hence every linear order in
, and hence every linear order in  is blanketed by
is blanketed by . We conclude that
. We conclude that  covers
covers , as desired.
, as desired.
Now, assume that 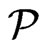 is a cover of
is a cover of 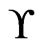 of cardinality at most
of cardinality at most . By previous observations, we must have
. By previous observations, we must have , for some set
, for some set  of cardinality at most
of cardinality at most . Since
. Since 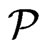 covers
covers ,
,  must blanket
must blanket  and
and . Let
. Let  be any edge of
be any edge of , incident on vertices
, incident on vertices 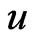 and
and . Without loss of generality, we may assume that
. Without loss of generality, we may assume that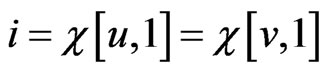 . There are two maximal posets that blanket
. There are two maximal posets that blanket 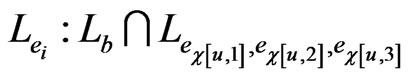 and
and
 . One of these posets must be in
. One of these posets must be in .
.
Moreover, we may assume that  contains only orders of this form, since each such order blankets
contains only orders of this form, since each such order blankets , and the only other orders for
, and the only other orders for 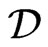 to blanket are the
to blanket are the ’s. Define
’s. Define

Because  blankets all of the
blankets all of the ’s, we conclude that
’s, we conclude that 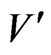 is a vertex cover of G of cardinality
is a vertex cover of G of cardinality  , as desired.
, as desired.
The theorem follows.
4. Cover Relations
In this section, we examine properties of cover relations in linear orders and their consequences for poset covers.
Let  be a poset, thought of as a transitive DAG. Then, a topological sort of
be a poset, thought of as a transitive DAG. Then, a topological sort of  yields an order
yields an order  on
on  such that
such that  implies
implies . Assume that
. Assume that  is not a linear order. Then there exist
is not a linear order. Then there exist  such that
such that . There exists at least one topological sort of
. There exists at least one topological sort of  in which
in which  appears to the left of
appears to the left of , and there exists at least one topological sort of
, and there exists at least one topological sort of  in which
in which 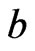 appears to the left of
appears to the left of . (This follows from alternate choices available to the depth-first search used to construct a topological sort. See [41].) Select a topological sort that makes
. (This follows from alternate choices available to the depth-first search used to construct a topological sort. See [41].) Select a topological sort that makes  and
and , where
, where . In that case, we obtain a proper extension
. In that case, we obtain a proper extension 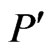 of
of  in which
in which  by adding
by adding  to the DAG and taking the transitive closure. Moreover, we have
to the DAG and taking the transitive closure. Moreover, we have , since the existence of
, since the existence of  such that
such that  contradicts
contradicts . We have just demonstrated the following.
. We have just demonstrated the following.
Lemma 5 Let  be a poset, and let
be a poset, and let  satisfy
satisfy . Let
. Let

Then  is a poset,
is a poset, 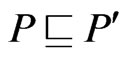 , and
, and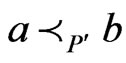 .
.
Theorem 6 Let  be a poset that is not a linear order, and let
be a poset that is not a linear order, and let  satisfy
satisfy . Then there exists a proper extension
. Then there exists a proper extension  of
of  such that
such that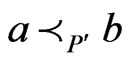 .
.
Proof. First, suppose that there exists a  that is incomparable to
that is incomparable to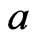 . By Lemma 5, there exists a poset
. By Lemma 5, there exists a poset  such that
such that  and
and . Moreover,
. Moreover, 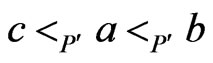 , so, by the definition of
, so, by the definition of .
.
Second, the case of there being a  that is incomparable to
that is incomparable to 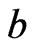 is handled analogously.
is handled analogously.
Finally, we have the case that no element is incomparable either to  or to
or to . Let
. Let  be such that
be such that  and
and . (Such a pair
. (Such a pair  must exist, since
must exist, since  is not a linear order.) If either
is not a linear order.) If either  and
and  or
or  and
and , then adding
, then adding 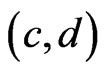 to the DAG for
to the DAG for  and taking the transitive closure gives us the desired poset. The case
and taking the transitive closure gives us the desired poset. The case  and
and  (or vice versa) is impossible, since
(or vice versa) is impossible, since  and
and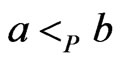 . There are no other cases, since
. There are no other cases, since .
.
The theorem follows.
Theorem 7 Let 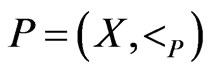 be a poset, and let
be a poset, and let  satisfy
satisfy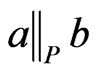 . Then there exists a linear order
. Then there exists a linear order  such that
such that 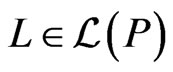 and
and . Moreover, for every linear extension
. Moreover, for every linear extension  of
of  in which
in which , there exists a unique linear extension
, there exists a unique linear extension
 of
of  such that
such that  and
and .
.
Proof. By Lemma 5, there exists a poset  such that
such that  and
and . By applying Theorem 6 iteratively to
. By applying Theorem 6 iteratively to , we ultimately obtain a linear order
, we ultimately obtain a linear order  that is an extension of
that is an extension of 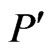 (and hence of
(and hence of ) such that
) such that .
.
Now, let  be a linear extension of
be a linear extension of  in which
in which . Let
. Let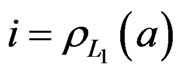 ; then
; then . Let
. Let
 . Let
. Let
 . Then
. Then  is a poset on
is a poset on  such that
such that  and such that
and such that  and
and 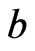 are incomparable in
are incomparable in . Moreover,
. Moreover,  , so
, so  is a linear extension of
is a linear extension of  in which
in which .
.
The theorem follows.
Theorem 8 Let 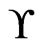 be a set of linear orders on
be a set of linear orders on . Let
. Let  be an element of
be an element of . Let
. Let  satisfy
satisfy . Let
. Let  be a partial cover of
be a partial cover of  including
including . If
. If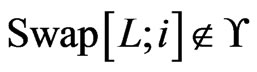 , then
, then  and
and  are comparable in
are comparable in  and
and .
.
Proof. Suppose that . First assume that
. First assume that  and
and  are comparable in
are comparable in . Then it must be true that
. Then it must be true that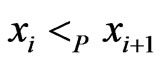 , since
, since  covers
covers  in
in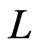 . For the same reason, there is no
. For the same reason, there is no  such that
such that . Hence,
. Hence, .
.
It remains to show that  and
and 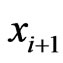 are comparable in
are comparable in . To obtain a contradiction, assume that
. To obtain a contradiction, assume that  and
and  are incomparable in
are incomparable in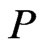 . By Theorem 7, there exists a unique linear extension
. By Theorem 7, there exists a unique linear extension  of
of 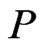 such that
such that 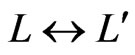 and
and . Necessarily,
. Necessarily,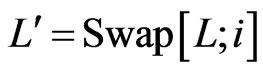 . Since
. Since  but
but , we have a contradiction to the fact that
, we have a contradiction to the fact that  is a partial cover of
is a partial cover of  including
including . The contradiction establishes that
. The contradiction establishes that  and
and  are comparable in
are comparable in . The theorem follows.
. The theorem follows.
We next characterize a set  of linear orders that is covered by a single poset. The ordered pair
of linear orders that is covered by a single poset. The ordered pair 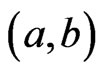 is a cover relation for
is a cover relation for  if there exists an
if there exists an  and an
and an  such that
such that ,
,  , and
, and . If
. If  is a cover relation for
is a cover relation for , then any poset P that partially covers
, then any poset P that partially covers  including
including  must satisfy
must satisfy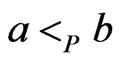 . An
. An  cover sequence of length
cover sequence of length  for
for  is a sequence
is a sequence  such that
such that  is a cover relation for
is a cover relation for , for
, for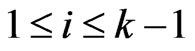 . If there is an
. If there is an  cover sequence for
cover sequence for , then any poset
, then any poset  that covers
that covers  must satisfy
must satisfy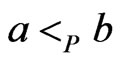 .
.
Theorem 9 A set  of linear orders is the set of linear extensions of a single poset if and only if, for every
of linear orders is the set of linear extensions of a single poset if and only if, for every  for which
for which , exactly one of the following holds: 1)
, exactly one of the following holds: 1)  for some
for some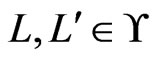 ; 2) there is an
; 2) there is an  cover sequence for
cover sequence for ; or 3) there is a
; or 3) there is a  cover sequence for
cover sequence for .
.
Proof. For one direction, assume that there exists a poset  such that
such that  is the set of linear extensions of
is the set of linear extensions of . Let
. Let  satisfy
satisfy .
.
First, suppose . By Theorem 7, there exists a linear extension
. By Theorem 7, there exists a linear extension  of
of  for which
for which  and another linear extension
and another linear extension  of
of  for which
for which  and
and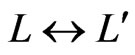 . Then, 1) holds. Neither 2) nor 3) holds, since those imply that
. Then, 1) holds. Neither 2) nor 3) holds, since those imply that  and
and 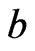 are comparable in
are comparable in .
.
Now suppose that . (The case
. (The case  is symmetric). Then 1) does not hold, since that implies that
is symmetric). Then 1) does not hold, since that implies that . Also 3) does not hold, since that implies that
. Also 3) does not hold, since that implies that . To demonstrate 2), it remains to construct an
. To demonstrate 2), it remains to construct an  cover sequence for
cover sequence for . The first case is
. The first case is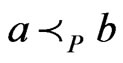 . Then, by repeated application of Theorem 6, there exists a linear extension
. Then, by repeated application of Theorem 6, there exists a linear extension  of
of  such that
such that . Let
. Let . Then,
. Then, . Hence,
. Hence, 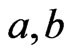 is an
is an 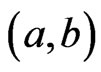 cover sequence for
cover sequence for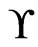 . More generally, we can write
. More generally, we can write  for some
for some 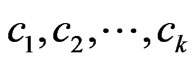 such that
such that  for
for . Then
. Then  is also an
is also an  cover sequence for
cover sequence for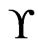 .
.
For the other direction, assume that, for every  for which
for which , exactly one of 1), 2), or 3) holds. Take
, exactly one of 1), 2), or 3) holds. Take  to be the poset generated by all the ordered pairs
to be the poset generated by all the ordered pairs  such that
such that  is a cover sequence for
is a cover sequence for . We need to show that
. We need to show that  equals the set of linear extensions of
equals the set of linear extensions of . There are two cases to consider for each linear order
. There are two cases to consider for each linear order . Let
. Let .
.
Case 1.
 . To obtain a contradiction, assume that
. To obtain a contradiction, assume that 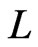 is not a linear extension of
is not a linear extension of . Then there exist
. Then there exist  and
and  such that
such that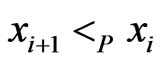 . Let
. Let  satisfy
satisfy . Then,
. Then,  is an
is an  cover sequence for
cover sequence for  and hence 2) holds for
and hence 2) holds for  and
and , but not 1) or 3). Let
, but not 1) or 3). Let . Since 1) does not hold, we have
. Since 1) does not hold, we have . But then
. But then  is a cover sequence for
is a cover sequence for , a contradiction to the fact that 3) does not hold. In this case, we conclude that
, a contradiction to the fact that 3) does not hold. In this case, we conclude that  is a linear extension of
is a linear extension of .
.
Case 2.
 . Without loss of generality, we may assume that there exist
. Without loss of generality, we may assume that there exist  and
and  such that
such that  and
and  . Since
. Since , we have that
, we have that  is a cover sequence for
is a cover sequence for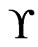 . Hence,
. Hence, 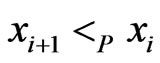 and
and  cannot be a linear extension of
cannot be a linear extension of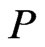 .
.
We conclude that  is precisely the set of linear extensions of
is precisely the set of linear extensions of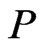 .
.
The theorem follows.
5. A Partial Cover Algorithm
In this section, we present an algorithm for finding a poset that is a partial cover with a maximal set of linear extensions.
5.1. Some Intuition
Intuition for designing an algorithm to find a partial poset cover for a set 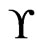 of linear orders is developed first. It suffices to take a single
of linear orders is developed first. It suffices to take a single 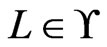 and identify a single poset
and identify a single poset  that is a partial cover of
that is a partial cover of  including
including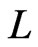 . Observe that
. Observe that  is such a poset but is not satisfactory if we can construct a poset
is such a poset but is not satisfactory if we can construct a poset 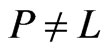 that covers more of
that covers more of . We use the swap graph
. We use the swap graph  to direct construction of a more satisfactory
to direct construction of a more satisfactory .
.
During the process of constructing , we maintain a specification for a set of posets, each of which covers a constructed set
, we maintain a specification for a set of posets, each of which covers a constructed set . We also maintain a set
. We also maintain a set  consisting of linear orders, including
consisting of linear orders, including , that have already been chosen to be covered by the final constructed poset. This specification consists of two kinds of information: some
, that have already been chosen to be covered by the final constructed poset. This specification consists of two kinds of information: some 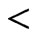 relations and some
relations and some  relations. These relations must be consistent, that is, there must be at least one poset that satisfies them all. A bit more formally, the
relations. These relations must be consistent, that is, there must be at least one poset that satisfies them all. A bit more formally, the 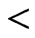 relations can be specified by a set
relations can be specified by a set  of ordered pairs, while the
of ordered pairs, while the 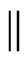 relations can be specified by a set
relations can be specified by a set  of unordered pairs. The specified set of posets is then
of unordered pairs. The specified set of posets is then .
.
 will be maintained to satisfy the following property. Let
will be maintained to satisfy the following property. Let  be arbitrary, and let
be arbitrary, and let  be any cover relation of
be any cover relation of . Let
. Let . If
. If , then we require that
, then we require that . The rational for this requirement is that every poset
. The rational for this requirement is that every poset  that covers
that covers  and does not cover
and does not cover  satisfies the relation
satisfies the relation . As a side effect, every
. As a side effect, every 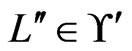 for which
for which  can be eliminated from further consideration for inclusion in
can be eliminated from further consideration for inclusion in .
.
 will be maintained to satisfy the following property. Again, let
will be maintained to satisfy the following property. Again, let 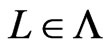 be arbitrary, and let
be arbitrary, and let  be any cover relation of
be any cover relation of . Let
. Let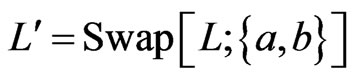 . If
. If , then we require that
, then we require that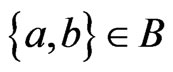 . The rational for this requirement is that every poset
. The rational for this requirement is that every poset  that covers both
that covers both  and
and  satisfies the relation
satisfies the relation . As a side effect, every
. As a side effect, every  for which the
for which the  adjacency is not in
adjacency is not in  can be eliminated from further consideration for inclusion in
can be eliminated from further consideration for inclusion in .
.
We will need these definitions. Let  be distinct, and let
be distinct, and let  be a linear order. The
be a linear order. The  -interchange of L is the linear order that is the same as
-interchange of L is the linear order that is the same as  except a and b have been exchanged. Let
except a and b have been exchanged. Let  be a sequence of linear orders such that
be a sequence of linear orders such that , for
, for , so that the sequence is a path
, so that the sequence is a path 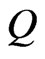 in
in . Let
. Let 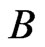 be a subset of
be a subset of
 .
.  is
is  -labeled if, for
-labeled if, for
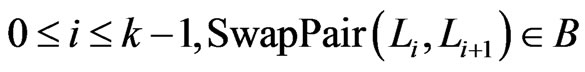 . A path
. A path
 in
in 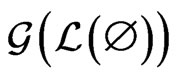 is the
is the  -mirror path of
-mirror path of  if, for
if, for ,
, 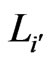 is the
is the  -interchange of
-interchange of .
.
5.2. The Algorithm
Figure 2 contains pseudocode for the algorithm PartialCover . It works by adding linear orders from
. It works by adding linear orders from 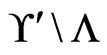 to
to  one at a time, while maintaining the required properties for A and B. The subroutine Trim in Figure 3 is used to ensure that the required property for
one at a time, while maintaining the required properties for A and B. The subroutine Trim in Figure 3 is used to ensure that the required property for 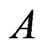 is maintained. The addition of a linear order to
is maintained. The addition of a linear order to  (Step 9) can add at most one new unordered pair to B (Step 10).
(Step 9) can add at most one new unordered pair to B (Step 10).
We illustrate the algorithm with the example having

and . Figure 4 contains the swap graph.
. Figure 4 contains the swap graph.
The call to Trim in Step 5 finds that  is not in
is not in , so any linear orders in
, so any linear orders in  for which 4 is less than 3 should be deleted. In this case, there is no such linear order in
for which 4 is less than 3 should be deleted. In this case, there is no such linear order in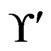 . After Step 6,
. After Step 6,  and
and .
.
The first time that Step 8 is executed in Partial-Cover, 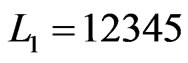 and
and . (There are three choices for
. (There are three choices for . This is just one of them.) Then
. This is just one of them.) Then
 (Step 9) and
(Step 9) and  (Step 10). The call to Trim in Step 11 finds that
(Step 10). The call to Trim in Step 11 finds that  is not in
is not in . The resulting cover relation
. The resulting cover relation  is not new, so
is not new, so  remains
remains . The while loop from Steps 13 to 21 has only the swap pair
. The while loop from Steps 13 to 21 has only the swap pair  to work with. Linear order 32154 is missing its
to work with. Linear order 32154 is missing its  swap partner, 31254. Hence, 32154 is deleted from
swap partner, 31254. Hence, 32154 is deleted from , which is now
, which is now

The second time that Step 8 is executed, 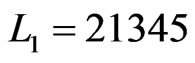 and L2 = 23145. Then
and L2 = 23145. Then  (Step 9) and
(Step 9) and  (Step 10). The call to Trim in Step 11 finds that 23415 is not in
(Step 10). The call to Trim in Step 11 finds that 23415 is not in . The resulting cover relation
. The resulting cover relation 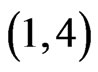 is new, so A is extended to
is new, so A is extended to  . None of the linear orders in
. None of the linear orders in  has 4 less than 1, so the call to Trim does not change
has 4 less than 1, so the call to Trim does not change . The while loop from Steps 13 to 21 now has the swap pair
. The while loop from Steps 13 to 21 now has the swap pair  to work with. Linear order
to work with. Linear order  is missing its
is missing its 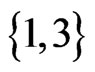 swap partner,
swap partner,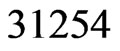 . Hence,
. Hence, 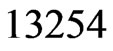 is deleted from
is deleted from , which is now
, which is now

The third time that Step 8 is executed,  and
and . Then
. Then
 (Step 9) and
(Step 9) and
 (Step 10). The call to Trim in Step 11 finds that
(Step 10). The call to Trim in Step 11 finds that 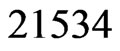 is not in
is not in . The resulting cover relation
. The resulting cover relation  is new, so
is new, so 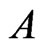 is extended to
is extended to
 . None of the linear orders in
. None of the linear orders in  has 5 less than 3, so the call to Trim does not change
has 5 less than 3, so the call to Trim does not change . The while loop from Steps 13 to 21 now has the swap pair
. The while loop from Steps 13 to 21 now has the swap pair  to work with. Linear orders 32145, 31245, and 13245 are missing their
to work with. Linear orders 32145, 31245, and 13245 are missing their  swap part-
swap part-
ners. Hence, they are deleted from , which is now
, which is now

The fourth time that Step 8 is executed,  and
and . Then
. Then
 (Step 9) and
(Step 9) and
 (Step 10). The call to Trim in Step 11 finds that
(Step 10). The call to Trim in Step 11 finds that  and
and 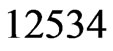 are not in
are not in . The resulting cover relations are
. The resulting cover relations are  and
and , so
, so  is extended to
is extended to . None of the linear orders in
. None of the linear orders in  has 3 less than 2, so the call to Trim does not change
has 3 less than 2, so the call to Trim does not change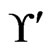 . The while loop from Steps 13 to 21 has no new swap pairs to work with. Hence, there are no further linear orders to delete from
. The while loop from Steps 13 to 21 has no new swap pairs to work with. Hence, there are no further linear orders to delete from , which remains
, which remains

The fifth and last time that Step 8 is executed,  and
and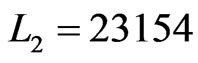 . Then
. Then
 (Step 9) and
(Step 9) and
 (Step 10). The call to Trim in Step 11 finds that
(Step 10). The call to Trim in Step 11 finds that 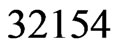 and
and  are not in
are not in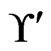 . The resulting cover relations are
. The resulting cover relations are , which is not new, and
, which is not new, and , which is new, so
, which is new, so 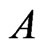 is extended to
is extended to . None of the linear orders in
. None of the linear orders in  has 3 less than 2 or 5 less than 1, so the call to Trim does not change
has 3 less than 2 or 5 less than 1, so the call to Trim does not change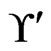 . The while loop from Steps 13 to 21 has no new swap pairs to work with. Hence, there are no further linear orders to delete from
. The while loop from Steps 13 to 21 has no new swap pairs to work with. Hence, there are no further linear orders to delete from , which remains
, which remains

At this point, .
.
The resulting poset  has the cover relations in
has the cover relations in , namely,
, namely, 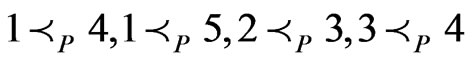 , and
, and . The set of linear extensions of
. The set of linear extensions of  is exactly the final value of
is exactly the final value of , namely,
, namely,  .
.
5.3. Proof of Correctness
We assume that the following loop invariants hold each time that the test at the top of the while loop body (Step 7) is executed.
1) .
.
2)  is a connected graph, and
is a connected graph, and  is a connected graph.
is a connected graph.
3) The directed graph 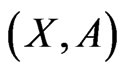 contains no cycles.
contains no cycles.
4) Every element of  is a linear extension of
is a linear extension of , that is,
, that is, .
.
5) The set  equals the set of ordered pairs
equals the set of ordered pairs
 for which there exists
for which there exists 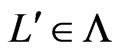 such that
such that
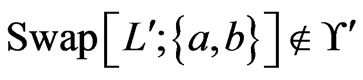 .
.
6) 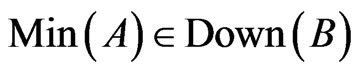 and consequently
and consequently  .
.
7) The set  equals the set of unordered pairs
equals the set of unordered pairs  such that
such that  and such that there exist
and such that there exist  satisfying
satisfying .
.
8) Let  be a
be a  -labeled path of linear orders such that
-labeled path of linear orders such that  and
and  and such that
and such that  is a shortest
is a shortest  -labeled path from
-labeled path from  to
to . Let
. Let 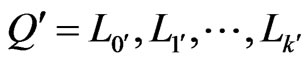 be the
be the  -mirror path for
-mirror path for . Then, all of the
. Then, all of the  's are in
's are in , and either all of the
, and either all of the ’s are in
’s are in  or none of them are.
or none of them are.
Together, these invariants suffice to demonstrate the correctness of Partial-Cover, culminating in Theorem 11.
Every execution of subroutine Trim enforces Invariant 5.
Invariant 2 is guaranteed by Steps 6 and 22 and by the way that linear orders are selected for addition to  (Step 8).
(Step 8).
Invariants 1 and 2 guarantee that, whenever Step 8 is reached, there is a suitable  pair to select.
pair to select.
The fact that  is guaranteed through the initialization in Step 3 and the fact that any change to
is guaranteed through the initialization in Step 3 and the fact that any change to 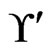 always selects a subset of
always selects a subset of .
.
Initialization. After initialization (Steps 2 through 6), all invariants are true for the first execution of Step 7, for the following reasons. We have  and
and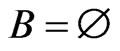 . The execution of Trim (Step 5) ensures that Invariants 4 and 5 hold, while maintaining
. The execution of Trim (Step 5) ensures that Invariants 4 and 5 hold, while maintaining  (Invariant 1). Step 6 guarantees Invariant 2. Invariant 3 holds because the only order relations in
(Invariant 1). Step 6 guarantees Invariant 2. Invariant 3 holds because the only order relations in 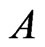 are cover relations in
are cover relations in . The fact that
. The fact that  makes Invariants 6, 7, and 8 true vacuously.
makes Invariants 6, 7, and 8 true vacuously.
Execution of the loop body. The fact that 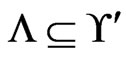 requires that the algorithm never deletes an element of
requires that the algorithm never deletes an element of  from
from  in Step 19 or in Trim. That fact also implies
in Step 19 or in Trim. That fact also implies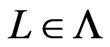 , since
, since 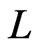 is initially put in
is initially put in  (Step 2) and could only be deleted in Step 19 or in Trim.
(Step 2) and could only be deleted in Step 19 or in Trim.
The algorithm never deletes an element of  from
from 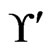 in Trim. To obtain a contradiction, assume that
in Trim. To obtain a contradiction, assume that  is deleted in Step 12 of Trim and that it is the first element of
is deleted in Step 12 of Trim and that it is the first element of  deleted. The deletion of
deleted. The deletion of 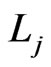 is caused by a sequence
is caused by a sequence  such that
such that , for
, for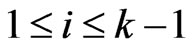 , and
, and . For each
. For each  satisfying
satisfying , there exists an
, there exists an 
such that , and
, and . There is a path in
. There is a path in  from
from  to
to 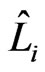 that does not contain an edge with swap pair
that does not contain an edge with swap pair , since
, since  contradicts
contradicts . Consequently,
. Consequently,  and
and  are in the same order in
are in the same order in  and in
and in , which implies that
, which implies that . Taken together, these relations imply that
. Taken together, these relations imply that , a contradiction to
, a contradiction to . We conclude that
. We conclude that  is, in fact, not deleted in Trim.
is, in fact, not deleted in Trim.
The algorithm never deletes an element of  from
from  in Step 19. The deletion of an element
in Step 19. The deletion of an element 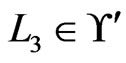 depends on the swap pairs in
depends on the swap pairs in . More particularly, such a deletion would require a
. More particularly, such a deletion would require a  -labeled path in
-labeled path in  labeled from
labeled from  from
from  to some
to some  that has a swap pair from
that has a swap pair from  that goes to a linear order outside
that goes to a linear order outside . This cannot happen because of Invariant 8. We conclude that
. This cannot happen because of Invariant 8. We conclude that  is, in fact, not deleted in Step 19.
is, in fact, not deleted in Step 19.
Invariant 3 is maintained because the existence of a cycle in A implies that A and B are inconsistent.
Invariants 4 and 5 are maintained by Trim.
The consistency of A and B (Invariant 6) is maintained by Trim and the loop at Steps 15 through 21.
Invariant 7 is maintained by the way that elements are added to B (Step 10).
It remains to show that Invariant 8 holds; this is demonstrated in the following lemma.
Lemma 10 Each time that Step 8 is about to be executed, Invariant 8 holds.
Proof. Let  be a
be a  -labeled path of linear orders such that
-labeled path of linear orders such that ,
, 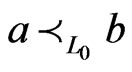 , and
, and 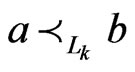 and such that
and such that  is a shortest
is a shortest  -labeled path from
-labeled path from  to
to . Let
. Let 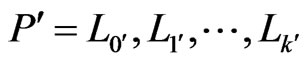 be the
be the  -mirror path for
-mirror path for .
.
To obtain a contradiction, assume that there is some 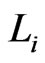 that is not in
that is not in . Let
. Let  be the first such. Then
be the first such. Then , so
, so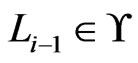 . Let
. Let . Since
. Since ,
,  cannot be in
cannot be in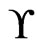 , since it would have been deleted in a previous iteration due to the swap pair
, since it would have been deleted in a previous iteration due to the swap pair  being in
being in . This is a contradiction. We conclude that all of the
. This is a contradiction. We conclude that all of the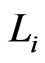 ’s are in
’s are in .
.
We next show that 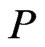 is not just a shortest
is not just a shortest  - labeled path but is also a shortest path in
- labeled path but is also a shortest path in . Let
. Let
 . For any path from
. For any path from 
to 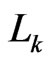 in
in , every
, every  must be the swap pair for some edge in the path. Consequently,
must be the swap pair for some edge in the path. Consequently, . Moreover, there is a path in
. Moreover, there is a path in  that uses swap pairs only from
that uses swap pairs only from  and each only once, so the length of every shortest path from
and each only once, so the length of every shortest path from 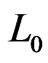 to
to  is
is . (Think about the swaps done by bubble sort; these give one such shortest path.) Since
. (Think about the swaps done by bubble sort; these give one such shortest path.) Since  is a shortest
is a shortest 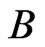 - labeled path from
- labeled path from 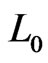 to
to , it must be a
, it must be a  -labeled path having
-labeled path having . Note that, therefore, no swap pair occurs more than once in
. Note that, therefore, no swap pair occurs more than once in .
.
We next show that 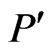 is a
is a  -labeled path. Since
-labeled path. Since 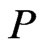 contains no swap pair more than once and since
contains no swap pair more than once and since  and
and , if there is a swap pair
, if there is a swap pair  labeling an edge of
labeling an edge of , we must also have the swap pair
, we must also have the swap pair  labeling another edge of
labeling another edge of , and vice versa. More succinctly,
, and vice versa. More succinctly, 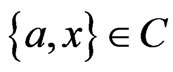 if and only if
if and only if . Let
. Let , for some
, for some  satisfying
satisfying
 . If
. If , then
, then
 . If
. If , then
, then
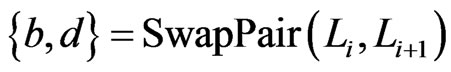 , which is in
, which is in  by the argument above. Similarly, if
by the argument above. Similarly, if , then
, then
 , which is in
, which is in  by the argument above. We conclude that
by the argument above. We conclude that  is a
is a  -labeled path and hence a
-labeled path and hence a  -labeled path.
-labeled path.
Finally, we show that either all of the ’s are in
’s are in  or none of them are. To obtain a contradiction, suppose that
or none of them are. To obtain a contradiction, suppose that  and that
and that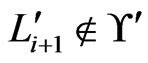 , for some
, for some  satisfying
satisfying . (The case
. (The case 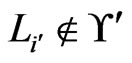 and
and  will yield a contradiction by an analogous argument.) But, in this case,
will yield a contradiction by an analogous argument.) But, in this case, 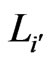 would have been deleted from
would have been deleted from  in an earlier iteration, a contradiction. From this contradiction, we conclude that either all of the
in an earlier iteration, a contradiction. From this contradiction, we conclude that either all of the ’s are in
’s are in  or none of them are.
or none of them are.
Hence, Invariant 8 holds.
The correctness and time complexity of the algorithm are now in view.
Theorem 11 Algorithm Partial-Cover returns a set
returns a set  such that
such that  is a partial cover of
is a partial cover of  including
including . The algorithm has time complexity
. The algorithm has time complexity
 .
.
Proof. The correctness of the algorithm follows from the prior discussion of the loop invariants.
For the time complexity, we first note that
 and
and .
.
We examine the subroutine Trim. Trim is executed once in Step 5; once for each addition to  (Step 11;
(Step 11;  times in total); and once for each deletion in Step 19 (Step 20;
times in total); and once for each deletion in Step 19 (Step 20; 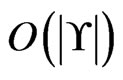 times in total). Hence, Trim is executed
times in total). Hence, Trim is executed 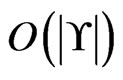 times. The loop in Steps 5 through 9 requires
times. The loop in Steps 5 through 9 requires  time for one execution. The time complexity to test coverage in Step 11 requires
time for one execution. The time complexity to test coverage in Step 11 requires  time. Hence, the loop in Steps 10 through 13 requires
time. Hence, the loop in Steps 10 through 13 requires  time for one execution. The while loop is executed
time for one execution. The while loop is executed 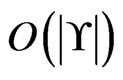 times, since each additional iteration of the loop because
times, since each additional iteration of the loop because  requires the reduction of the cardinality of
requires the reduction of the cardinality of  by at least one. We conclude that the total time spent in trim is
by at least one. We conclude that the total time spent in trim is
 .
.
It is easy to check that the complexity bound for all calls to Trim dominates the time complexity of the algorithm. Hence, the time complexity of Partial-Cover is
 , as required.
, as required.