1. Introduction
Concerned with the perturbed Navier-Stokes equations:
(1.1)
where 
is a smooth bounded domain with boundary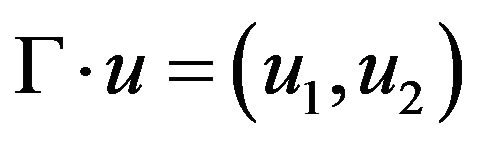
, and p, u is the velocity vector, 
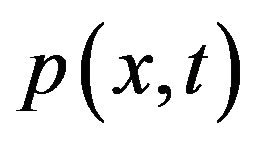is the pressure at x at time t, and 
is the kinematic viscosity, and f represents volume forces that are applied to the fluid, and
, where 
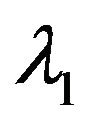is the first eigenvalue of A (see Remark 4). The Equation (1.1) is Navier-Stokes equations, as
, which show the existence of absorbing sets and the existence of a maximal attractor, the universal attractor, attractor in unbounded domain (see [1-5]). ACTA Mathematical Application Sinica. In [6], where they some interesting results, as
. In [7,8] Babin, Vishik and Abergel consider maximal attractors of semigroups corresponding to evolution differential equations, existence and finite dimensionality of global attractor for evolution equations on unbounded domains. In [9,10] A. Pazy consider Semigroups of linear operator and application to partial differential equation.
We need the following preliminaries:
Equations (1.1) are supplemented with a boundary condition. Two cases will be considered: The nonslip boundary condition. The boundary 
is solid and at rest; thus
(1.2)
The space-periodic case. Here 
and
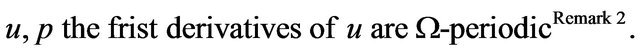(1.3)
Remark 1. If 
is solid but not rest, then the nonslip boundary condition is 
on 
where 
is the give velocity of
.
Remark 2. That is u and p take the same values at corresponding points of
.
Furthermore, we assume in this case that the average flow vanishes
(1.4)
When an initial-value problem is considered we supplement these equations with
(1.5)
For the mathematical setting of this problem we consider a Hilbert space H (see [8]) which is a close subspace of 
(
here).
In the nonslip case,
(1.6)
and in the periodic case
(1.7)
We refer the reader to R. Temam [2] for more details on these spaces and, in particular, a trace theorem showing that the trace of 
on 
exists and belong to 
when 
and
. The space H is endowed with the scalar product and the norm of 
denoted by 
and
.
Remark 3. 
and 
are the faces 
and
of
. The condition 
expresses the periodicity of
; 
is the space of 
satisfying (1.4).
Another useful space is 
a closed subspace of 
(1.8)
in the nonslip case and , in the space-periodic case,
(1.9)
where 
is define in [1]. In both case, v is endowed with the scalar product
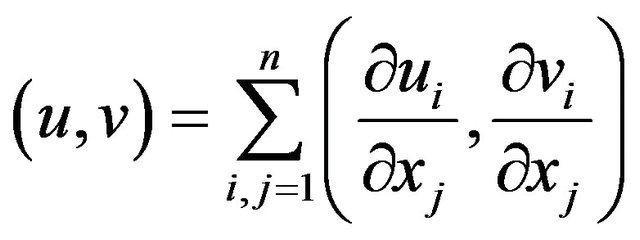
and the norm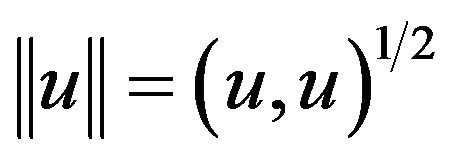
.
We denoted by A the linear unbounded operator in H which is associated with V, H and the scalar product
,
. The domain of A in H is denoted by
; A is self-adjoint positive operator in H. Also A is an isomorphism from 
onto H. The space 
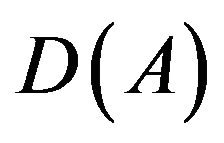can be fully characterized by using the regularity theory of linear elliptic systems (see [1,3]).
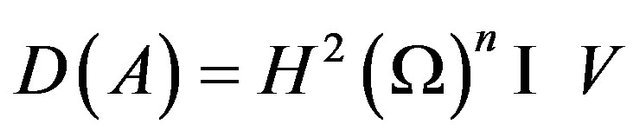
and 
in the nonslip and periodic cases; furthermore, 
is on 
a norm equivalent to that induced by 
Let 
be the dual of V; then H can be identified to a subspace of 
and we have
(1.10)
where the inclusions are continuous and each space is dense in the following one.
Remark 4. In the space-periodic case we have 
, 
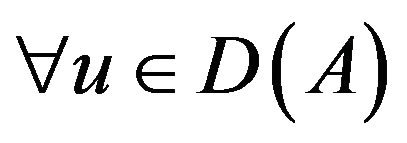, while in the nonslip case we have
, 
, where P is the orthogonal projector in 
on the space H. We can also say that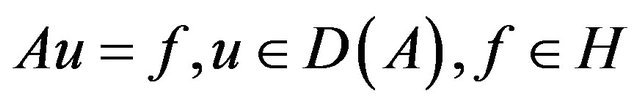 
is equivalent to saying that there exists 
such that
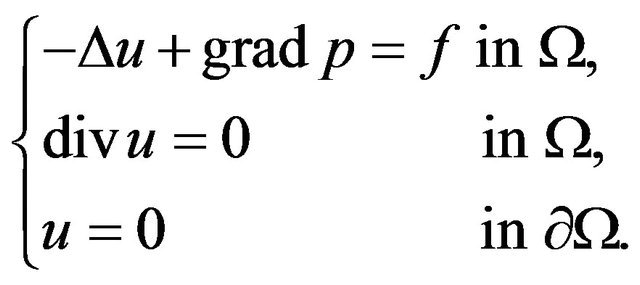
The operator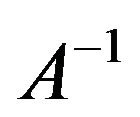 
is continuous from H into 
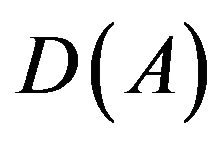and since the embedding of 
in 
is compact, the embedding of V in H is compact. Thus 
is a self-adjoint continuous compact operator in H, and by the classical spectral theorems there exists a sequence
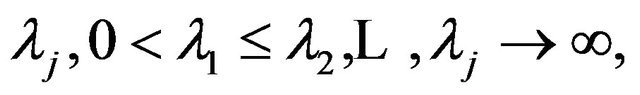
and a family of elements 
of 
which is orthonormal in H, and such that
(1.11)
We need the following main Result:
Lemma 1.1. (see [4]) (Uniform Gronwall Lemma) Let 
be three positive locally integrable function on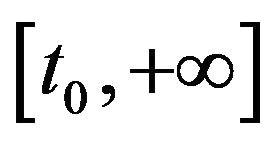 
such that 
is locally integrable on
, and satisfy
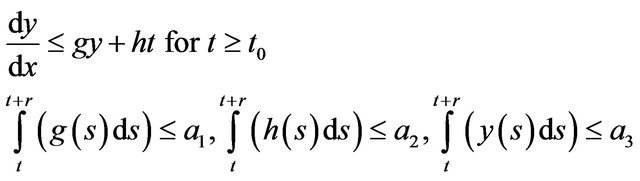
for 
where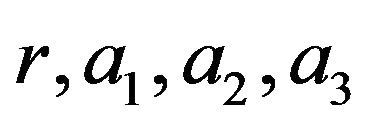 
are positive constant. Then
.
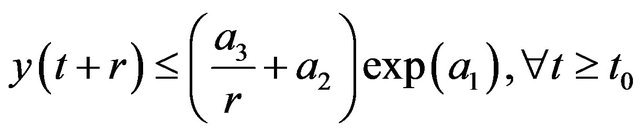The evolution of the dynamical system is described by a family of operators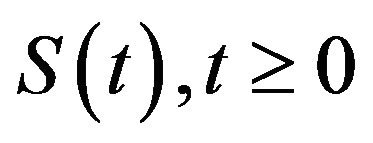
, that map H into itself and enjoy the usual semigroup properties (see [8]):
(1.12)
(1.13)
The operator 
are uniformly compact for t large. By this we mean that for every bounded set X there exists 
which may depend on X such that
(1.14)
for every bounded set
,
(1.15)
Of course, if H is Banach space, any family of operators satisfying (1.14) also satisfies (1.15) with
.
Theorem 1.2. (see [4]) We assume that H is a metric space and that the operators 
are given and satisfy (1.12), (1.13) and either (1.14) or (1.15). We also assume that there exists an open set 
and abounded set X of 
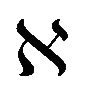such that X is absorbing in
. Then w-limt set of
, is a compact attractor which attracts the bounded set of
. It is the maximal bounded attractor in 
(for the inclusion relation). Furthermore, if H is a Banach space, if U is convex2, and the mapping 
is continuous from
, for every 
in H; then 
is connected too.
The rest of this paper is organized such that Section 2 contains a sketch of existence and uniqueness of solution of the equations; in Section 3 we show the existence of absorbing set and the existence of a maximal attractor; in Section 4 contain the proof of existence and uniqueness of solution of the equations, in Section 5 discussed the perturbation coefficients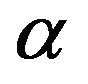
.
2. Existence and Uniqueness of Solution of the Equations
The weak from of the Navier-Stokes equations due to J. Leray [1-3] involves only u, as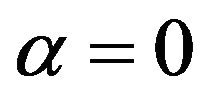
. It is obtained by multiply (1.1) by a test function v in V and integrating over
. Using the Green formula (1.1) and the boundary condition, we find that the term involving p disappears and there remains
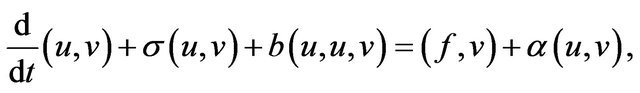(2.1)
where
(2.2)
whenever the integrals make sense. Actually, the from b is trilinear continuous on 
and in particular on V. We have the following inequalities giving various continuity properties of b:
(2.3)
where 
is an appropriate constant
.
An alternative from of (2.1) can be given using the operator 
and the bilinear operator 
from 
into 
defined by
(2.4)
we also set
and we easily see that (2.1) is equivalent to the equation
(2.5)
while (1.5) can be rewritten
(2.6)
We assume that f is in dependent of 
so that the dynamical system associated with (2.5) is autonomous
(2.7)
Existence and uniqueness results for (2.5) (2.6) are well know as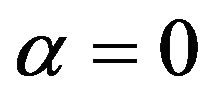 
(see [2,3]). The following theorem collects several classical results.
Theorem 1.3. Under the above assumption, for 
and 
given in 
t here exists a unique solution 
of (2.4) (2.5) satisfying
; Furthermore, 
is analytic in 
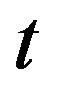with values in 
for
, and the mapping 
is continuous from 
into
; Finally, if
, then
. Some indications for the proof of Theorem 1.3 will be given in Section 4. This theorem allows us to define the operators
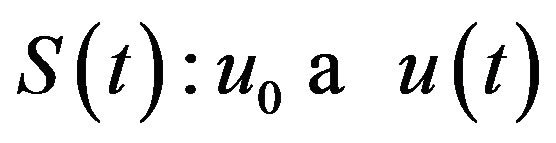
These operator enjoy the semigroup properties (1.12) and the are continuous from H into itself and even from H into
.
3. Absorbing Sets and Attractor
The part proof about global attractor is similar to the Temam’s book, but the exists of perturbation term is different from the Temam’s book, so we reprove it for integrality.
Theorem 1.4. The dynamical system associated with the tow-dimensional modified Navier-Stokes equations, supplemented by boundary (1.2) or (1.3), (1.4) possesses an attractor 
that is compact, connected,and maximal in H. 
attracts the bounded sets of H and 
is also maximal among the functional invariant set bounded in H.
Proof. We first prove the existence of an absorbing set in H. A first energy-type equality is obtained by taking the scalar product of (2.5) with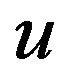
. Hence
(3.1)
We see that 
and there remains
(3.2)
We know that 
where 
is the first eigenvalue of
. Hence, we can majorize the right-hand side of (3.1) by
the estimates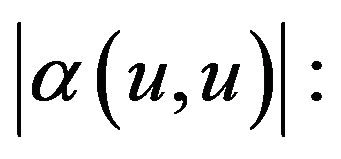 
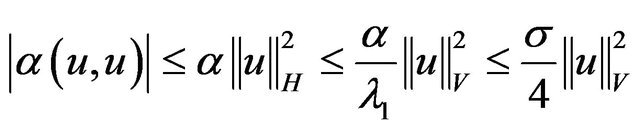
Hence we obtain
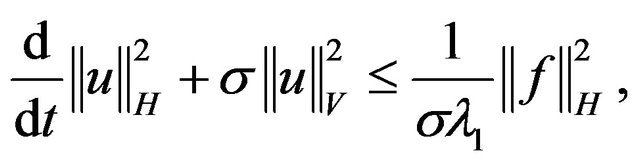(3.3)
(3.4)
Using the classical Gronwall Lemma, we obtain
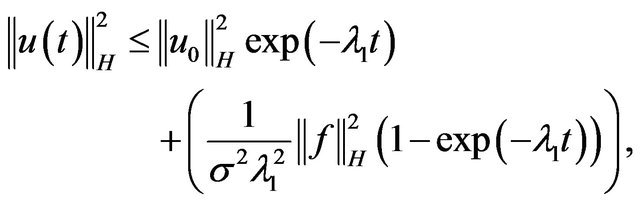(3.5)
Thus
(3.6)
We infer (3.5) that the ball 
of 
with 
are positively invariants for the semigroup
, and these balls are absorbing for any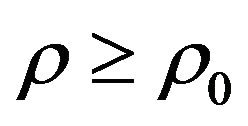
. We choose 
and included a ball 
of
, It is easy to deduce from (3.5) that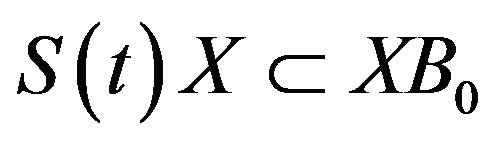 
for
, where
(3.7)
We the infer from (3.3), after integration in t, that
(3.8)
With the use of (3.6) we conclude that
(3.9)
and if 
and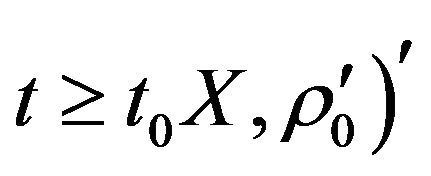
, then
(3.10)
1) Absorbing set in V An continue and show the existence of an absorbing set in V. For that purpose we obtain another energy-type equation by taking the scalar product of (2.5) with
. Since
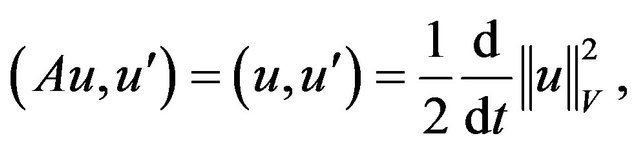
we find
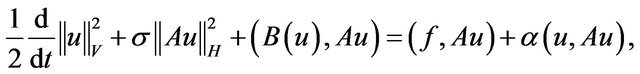
we writer
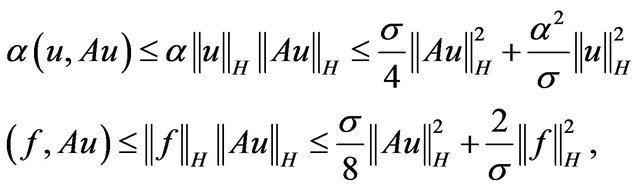
and using the second inequality (2.3)
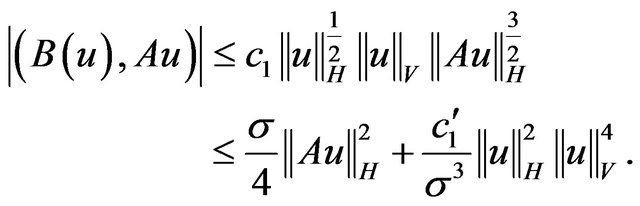
Hence
(3.12)
and since
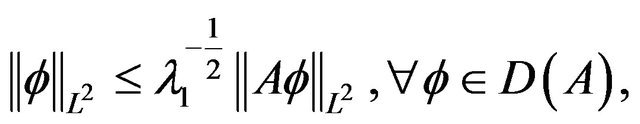(3.13)
We also have
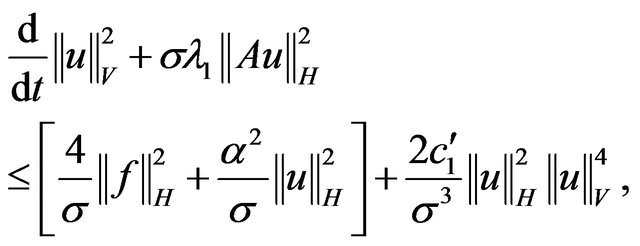(3.14)
We a priori estimate of 
follows easily from (3.14) by the classical Gronwall lemma, using the previous estimates on u. We are more interested in an estimate valid for large t. Assuming that 
belong to a bounded set X of H and that 
as in (3.7), we apply the uniform Gronwall lemma to (3.14) with 
replaced by
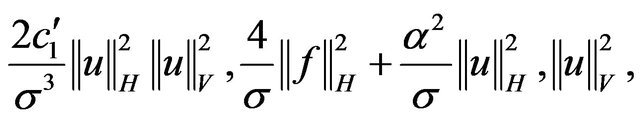
Thanks to (2.14), (2.18) we estimate the quantities 
in Lemma 1.1 by
(3.15)
and we obtain
(3.16)
as in (3.7). Let us fix 
and denote by 
the right-hand side of (2.24). We the conclude that the ball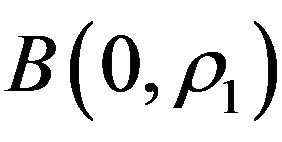 
of V, denoted by X1, is an absorbing set in V for the semigroup
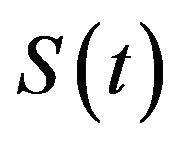. Furthermore, if X is any bounded set of H, then 
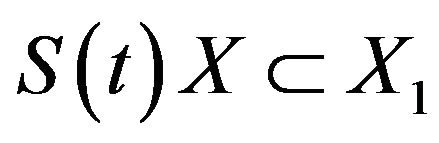for
. This shows the existence of an absorbing set in V, namely X, and also that the operators 
are uniformly compact, i.e., Theorem 1.1 is satisfied.
2) Maximal attractor All the assumption of Theorem 1.1 are satisfied and we deduce from this theorem the existence of a maximal attractor for modified Navier-Stokes equations. 
4. Proof of Theorem 1.3
The existence of a solution of (2.4) (2.5) that belong to
, is first obtain by the Faedo-Gakerkin (see [3]) method. We implement this approximation procedure with the function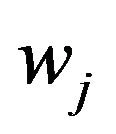 
representing the eigenvalues of A (see Remark 4). For each m we look for an approximate solution 
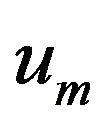of the form
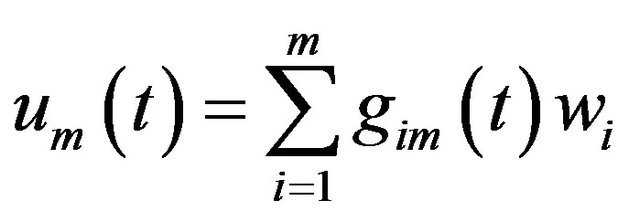
satisfying
(4.1)
(4.2)
where 
is projector in H (or V) on the space spanned by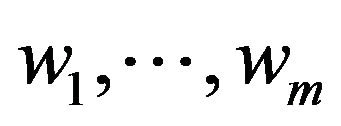
. Since A and 
commute, the relation (3.1) is also equivalent to
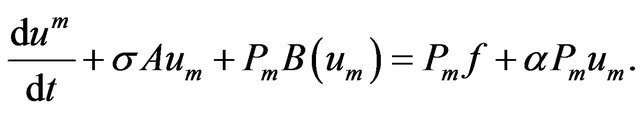(4.3)
We prove 
on 
is Lip continuous,
hence
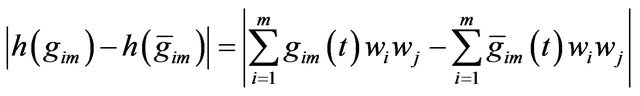
there is m, M such that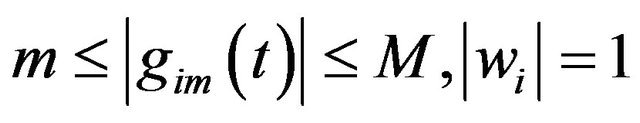
. When 
is established, and when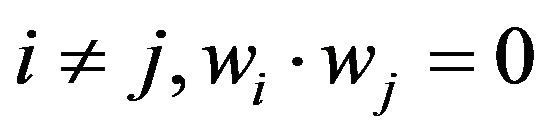 
is established, then
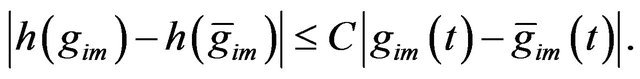
On both sides in the integral
, then
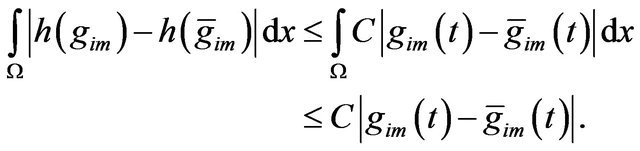
we writer
Hence 
on 
is Lip continuous. The existence and uniqueness of 
on some interval 
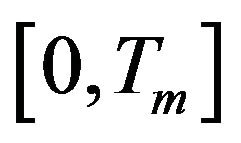is elementary and then
, because of the a priori estimates that we obtain for
. An energy equality is obtained by multiplying (4.1) by 
and summing these relations for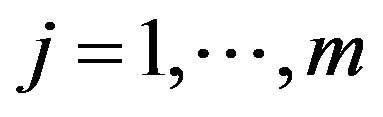
. We obtain (3.2) exactly with u replaced by 
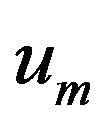and we deduce from this relation that
(4.4)
Due to (3.1) and the last inequality (2.3)
(4.5)
Therefor 
and 
remain bounded in 
and by (4.3)
(4.6)
By weak compactness it follows from (4.3) that there exists
, and a subsequence still denoted m, such that
(4.7)
Due to (4.6) and a classical compactness theorem (see [2]), we also have
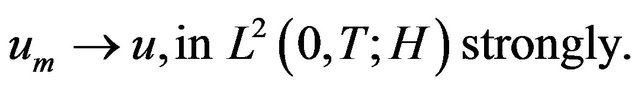(4.8)
This is sufficient to pass to the limit in (4.1)-(4.3) and we find (2.4), (2.5) at the limit. For (2.5) we simply observe that (4.7) implies that 
weakly in 
or even in
.
By (2.4), 
belong to 
and, u is in
. The uniqueness and continuous dependent of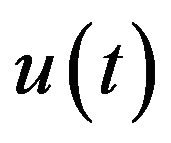 
on 
(in
) follow by standard using [2].
The fact that
, is proved by deriving further a priori estimates on
. They are obtained by multiplying (4.1) by 
and summing these relations for
. Using (1.11) we find a relation that is exactly (3.11) with 
replaced by
. we deduce form this relation that
(4.9)
At the limit we then find that u is in
. The fact that u in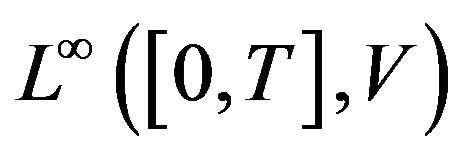 
then follows from an appropriate application of Lemma 3.2 [2].
Finally, the fact that u is analytic in t with values in 
results from totally different methods, for which the reader is referred to C. Foias and R. Temam [1] or R. Temam [3]. However, this property was given for the sake of completness and is never used here in an essential manner. 
5. The Limit-Behavior of Navier-Stokes Equation with Nonlinear Perturbation
We consider the limit-behavior of Navier-Stokes equation with nonlinear perturbation on the two dimensional space. we use the space which is given (1.6), (1.8). The main advantage we see is that applying the Gronwall lemma to the solution of problem (1.1) approaches a solution of Navier-Stokes equation on 
and
, as
.
Theorem 1.6. Under assumption (1.6), then the solution of 
of (1.1) is approximate solution of Navier-Stokes equations and this solution is stable, as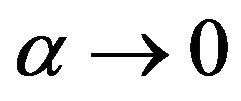
.
Proof. Let 
is a solution of (1.1), as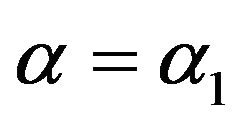
:
(5.1)
Let 
is a solution of (1.1), as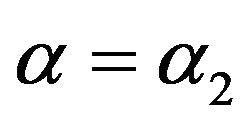
:
(5.2)
Utilizing (5.1)-(5.2) and let 
Hence
(5.3)
It is obtained by multiply (5.4) by a function 
in 
and integrating over
.
(5.4)
Using the second inequality (2.3) and 
is trilinear continuous:
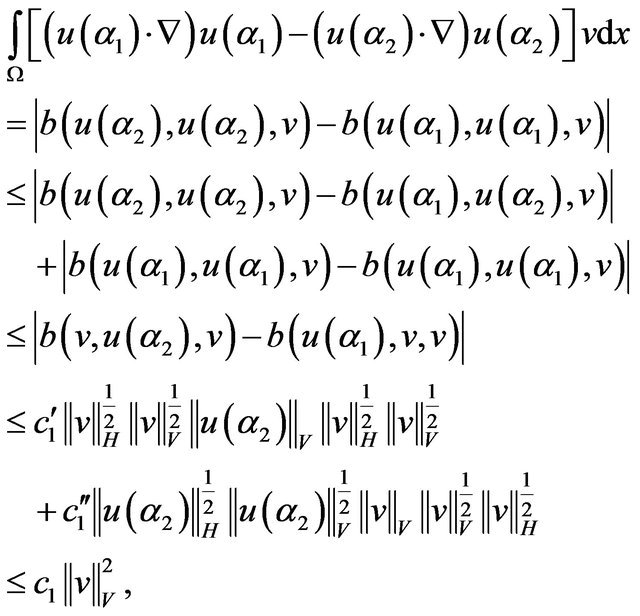
and
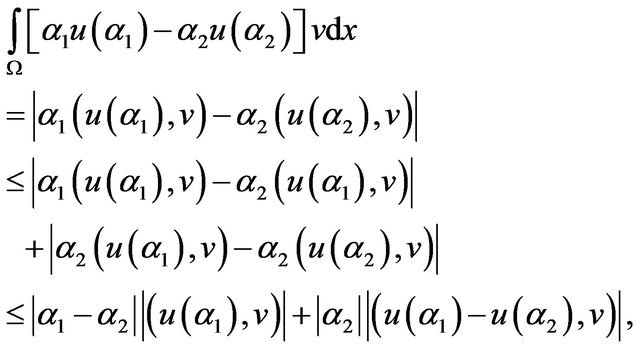
utilizing inequality (**), (3.6), (3.46) we estimate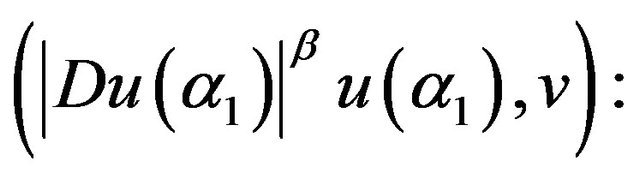 
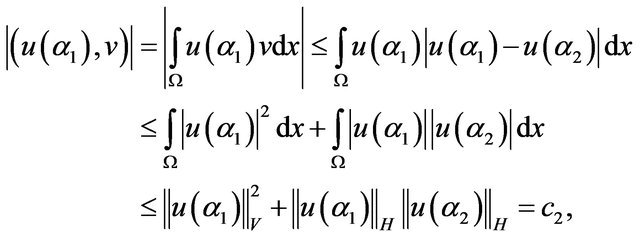
we write
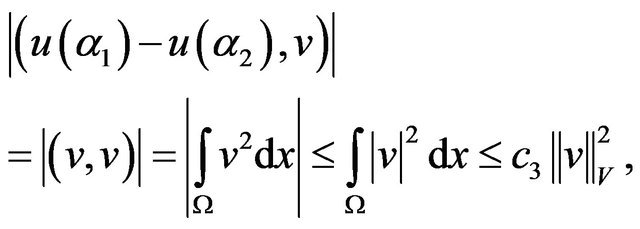
hence
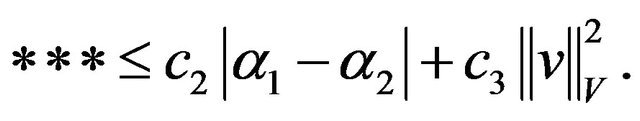
where 
is an appropriate constant. Hence
(5.5)
i.e.
(5.6)
Using the classical Gronwall Lemma, we obtain
(5.7)
where
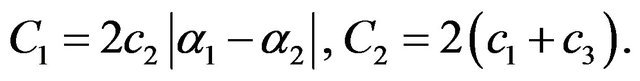
Notice that 
Thanks to
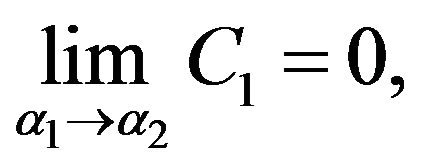
hence
Hence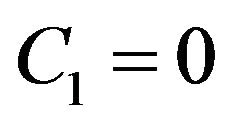
, 
as
, according to stable condition, thus this solution is stable. 
NOTES
#Corresponding author.