Set-Valued Non-Linear Random Implicit Quasivariational Inclusions ()
1. Introduction
The theory of variational inequality provides a natural and elegant framework for study of many seemingly unrelated free boundary value problems arising in various branches of engineering and mathematical sciences. Variational inequalities have many deep results dealing with nonlinear partial differential equations which play important and fundamental role in general equilibrium theory, economics, management sciences and operations research, see [1-3].
The quasi variational inequalities have been introduced by Bensoussan and Lions [1] and closely related to contact problems with friction in electrostatics and nonlinear random equations frequently arise in biological, physical and system sciences [4,5]. With the emergence of probabilistics functional analysis, the study of random operators became a central topic of this discipline [4,5]. The theory of resolvent operators introduced by Brezis [2] is closely related to the variational inequality problems; for applications we refer to [6-8].
Motivated by recent research work on random variational inequalities [9-14], in this paper we consider a class of set valued nonlinear random implicit quasi variational inclusions and a class of random proximal operator equations and establish an equivalence between them. We use the equivalence to suggest and analyzed some iterative algorithms for finding approximate solution of (1). Further we prove the existence of solution of this class of problem and discuss the convergence of iterative sequences generated by these random iterative algorithms.
2. Preliminaries
Let  be a measurable space and
be a measurable space and  a separable real Hilbert space with inner product
a separable real Hilbert space with inner product  and norm
and norm . We denote
. We denote ,
,  and
and  the class of Borel
the class of Borel  field in
field in  family of all nonempty power subsets of
family of all nonempty power subsets of  and the family of all nonempty compact subsets of
and the family of all nonempty compact subsets of  respectively.
respectively.
Definition 1. A mapping  is called measurable if for any
is called measurable if for any ,
, .
.
Definition 2. A mapping  is called a random operator if for any
is called a random operator if for any 
 is measurable.
is measurable.
Definition 3. A random operator T is said to be continuous if for any , the mapping
, the mapping  is continuous.
is continuous.
Given random set valued mappings
 and
and 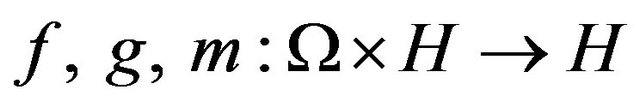 are the single valued mappings. Let
are the single valued mappings. Let  be a random set valued mapping such that for each fix
be a random set valued mapping such that for each fix ,
,  ,
,  is a maximal monotone mapping with
is a maximal monotone mapping with
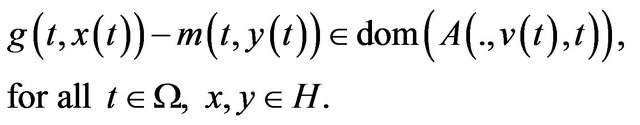
Throughout this paper, we will consider the following set valued nonlinear random implicit quasivariational inclusions for finding ,
, 
 ,
,  ,
,  ,
,
 ,
,  such that
such that
 (1)
(1)
where 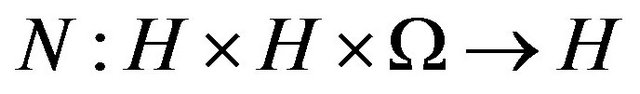 be the bifunction.
be the bifunction.
In deterministic case, the problem (1) is equivalent to the problem of the Ding and Park [15].
For a suitable choice of the operators A, g, m, f, N, T, V, G, P and E a number of known classes of variational inequalities, quasivariational inclusions can be obtained as special cases of problem, studied previously by many authors including Hassouni and Moudafi [16], Huang [17], Uko [18], Verma [13], Salahuddin [19], and Salahuddin and Ahmad [20].
Definition 4. If A is maximal monotone operator on H, then for a given constant  the proximal operator associated with A is defined by
the proximal operator associated with A is defined by
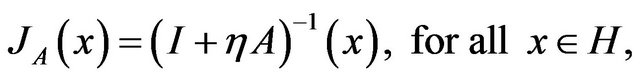
where I is the identity operator. It is also known that the operator A is maximal monotone if and only if the proximal operator JA is defined everywhere on the space. Furthermore, the proximal operator JA is single-valued and nonexpansive, i.e. for all ,
,

Remark 1. Since the operator  is a maximal monotone operator with respect to the first argument, we define
is a maximal monotone operator with respect to the first argument, we define

the generalized proximal operator associated with
 .
.
Related to the problem (1), we consider the problem of finding ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 such that
such that
 (2)
(2)
where  be the measurable function and
be the measurable function and
 .
.
Here  stand for an identity operator and
stand for an identity operator and
 is the random proximal operator. Equation of the type (2) is called random implicit proximal operator equations.
is the random proximal operator. Equation of the type (2) is called random implicit proximal operator equations.
3. Random Iterative Algorithm
In this section, we prove results which will establish eqivalence between the problems (1) and (2). Then we construct a number of iterative algorithms for solving problem (1).
Lemma 1. If ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 is a random solution set of problem (1) if and only if
is a random solution set of problem (1) if and only if ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 such that
such that

(3)
where  and
and  are two measurable functions and
are two measurable functions and here I stand for identity functions.
here I stand for identity functions.
Proof. Let ,
,  ,
, 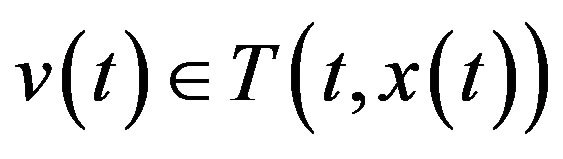 ,
,
 ,
,  ,
,  ,
,
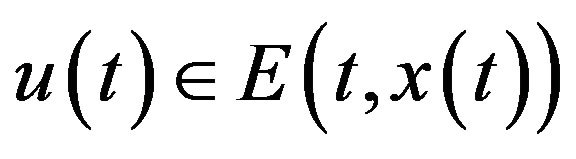 be the random solution set of (1). Then for a given measurable function
be the random solution set of (1). Then for a given measurable function ,
,

where  be the measurable mapping. This completes the proof.
be the measurable mapping. This completes the proof.
Theorem 1. The random problem (1) has a random solution set ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 if and only if random problem (2) has a random solution set
if and only if random problem (2) has a random solution set ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  where
where
 (4)
(4)
and
 (5)
(5)
Proof. Let ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
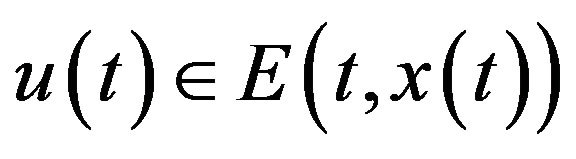 be a random solution set of (1). Then for a measurable function
be a random solution set of (1). Then for a measurable function ,
,


Take,

Then,
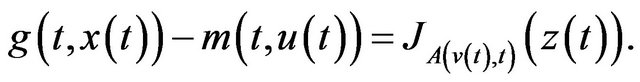
Thus,


That is,

where , completing the proof of Theorem 1.
, completing the proof of Theorem 1.
Theorem 1 implies that random problems (1) and (2) are equivalent, which allows us to suggest a number of iterative algorithms for solving problem (1). For a suitable rearrangement of the terms of the random Equation (2), we suggest the following algorithms:
1) The random problem (2) can be written as

which implies that

This random fixed point formulation allow us to suggest the following random iterative algorithm.
Algorithm 1. For given ,
,  ,
, 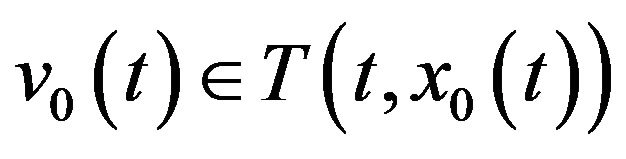 ,
,  ,
,
 ,
,  ,
,
 , compute
, compute ,
,  ,
,
 ,
,  ,
,  ,
,  and
and  by random iterative schemes,
by random iterative schemes,
 (6)
(6)

 (7)
(7)
2) The random problem (5) can be written as

This random fixed point formulation is used to suggest the following algorithm:
Algorithm 2. For given ,
, 
 ,
,  ,
,
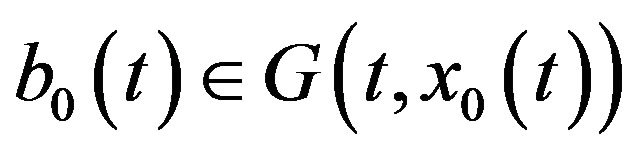 ,
,  ,
,
 , compute
, compute ,
,  ,
,
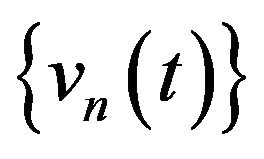 ,
,  ,
,  ,
,  and
and  by random iterative schemes,
by random iterative schemes,
 (8)
(8)

 (9)
(9)
4. Main Result
First we recall the following well known concepts.
Definition 5. A random mapping  is said to be 1) random strongly monotone, if there exists a measurable function
is said to be 1) random strongly monotone, if there exists a measurable function  such that
such that

2) random Lipschitz continuous, if there exists a measurable function  such that
such that

Definition 6. A random mapping 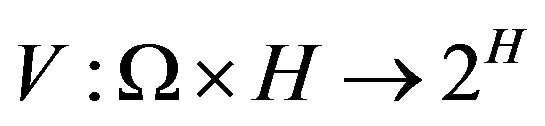 is said to be random relaxed monotone with respect to the first argument of a random mapping
is said to be random relaxed monotone with respect to the first argument of a random mapping
 , if there exists a measurable function
, if there exists a measurable function 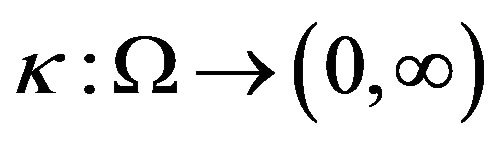 such that
such that
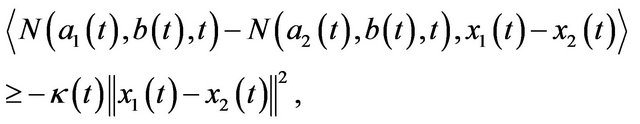
for all 


 .
.
Definition 7. A random mapping  is said to be random relaxed Lipschitz continuous with respect to the second argument of random mapping
is said to be random relaxed Lipschitz continuous with respect to the second argument of random mapping  if there exists a measurable mapping
if there exists a measurable mapping  such that
such that

for all 


 .
.
Definition 8. A random set-valued mapping  is said to be
is said to be  -Lipschitz continuous if there exists a measurable function
-Lipschitz continuous if there exists a measurable function 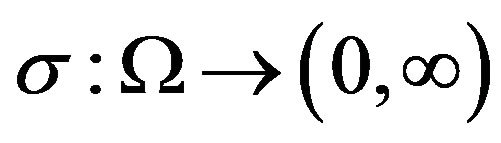 such that
such that

where  is a Hausdorff metric on
is a Hausdorff metric on .
.
Theorem 2. Let the random bifunction  be random Lipschitz continuous with respect to first and second arguments with measurable functions
be random Lipschitz continuous with respect to first and second arguments with measurable functions  respectively and random set valued mappings
respectively and random set valued mappings  be the random
be the random  -Lipschitz continuous with random coefficients
-Lipschitz continuous with random coefficients  respectively. Let the random mappings
respectively. Let the random mappings  be random Lipschitz continuous with random coefficients
be random Lipschitz continuous with random coefficients 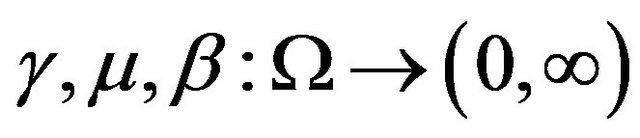 respectively and the random mapping g is the random strongly monotone with respect to the measurable map
respectively and the random mapping g is the random strongly monotone with respect to the measurable map . A random bifunction
. A random bifunction  is randomly relaxed monotone with respect to the first argument of
is randomly relaxed monotone with respect to the first argument of  with random coefficient
with random coefficient  and relaxed Lipschitz continuous with respect to the second argument of
and relaxed Lipschitz continuous with respect to the second argument of 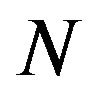 with random coefficient
with random coefficient . Let
. Let  be such that for each fixed
be such that for each fixed ,
,  ,
,  be a random maximal monotone satisfying
be a random maximal monotone satisfying
 for all
for all
 . Suppose that for any fix
. Suppose that for any fix ,
,  ,
,
 (10)
(10)
 (11)
(11)
where  be the measurable map, then there exists
be the measurable map, then there exists  such that
such that

 (12)
(12)


where,  ,
,
 ,
, 
Then there exist ,
,  ,
,
 ,
,  ,
,  ,
,
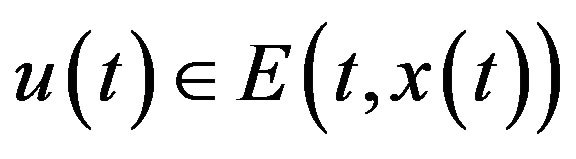 , satisfying (2) and (5) and random sequences
, satisfying (2) and (5) and random sequences ,
,  ,
,  ,
, 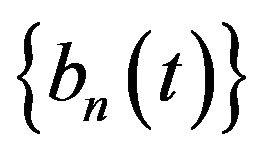 ,
,  ,
,
 and
and  generated by Algorithm 1, converge strongly to
generated by Algorithm 1, converge strongly to ,
,  ,
,  ,
,  ,
,  ,
,  and
and  in
in  for each
for each .
.
Proof. From Algorithm 1, we have
 (13)
(13)
Since N is randomly Lipschitz continuous with respect to first and second argument and V and  are random
are random  - Lipschitz continuous, we have
- Lipschitz continuous, we have
 (14)
(14)
Again  are randomly Lipschitz continuous and
are randomly Lipschitz continuous and  are random
are random  -Lipschitz continuous, we have
-Lipschitz continuous, we have
 (15)
(15)
 (16)
(16)
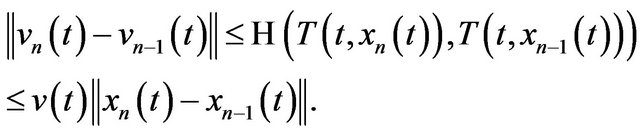 (17)
(17)
 (18)
(18)
Since  is random strongly monotone and from (18), we have
is random strongly monotone and from (18), we have
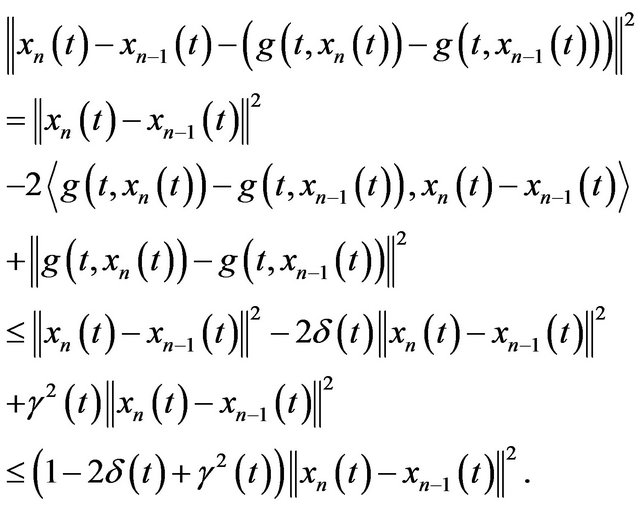 (19)
(19)
Since  is random relaxed monotone with respect to first argument and random relaxed Lipschitz continuous with second argument, we have
is random relaxed monotone with respect to first argument and random relaxed Lipschitz continuous with second argument, we have
 (20)
(20)
From (13)-(15), (19) and (20), we have
 (21)
(21)
where  and
and

Also from (6), (10), (11), (15) and (19), we obtain

which implies that
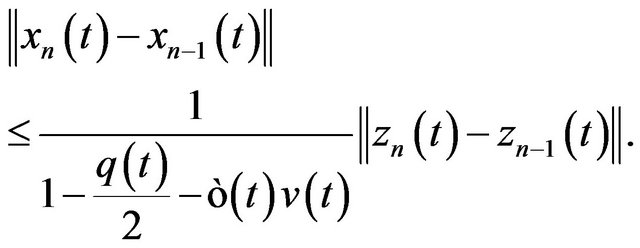 (22)
(22)
Adding (21) and (22), we obtain
 (23)
(23)
where,

From (12), it follows that  for each
for each . Consequently from (23), we see that the random sequence
. Consequently from (23), we see that the random sequence  is a Cauchy sequence in
is a Cauchy sequence in  for each
for each , that is there exists
, that is there exists  for fix
for fix  with
with  as
as . From (22), we know that the random sequence
. From (22), we know that the random sequence  is a Cauchy sequence in
is a Cauchy sequence in 
that is there exists  with
with  for each fix
for each fix . Also from the random Lipschitz continuity, we have
. Also from the random Lipschitz continuity, we have

which implies that the random sequences ,
, 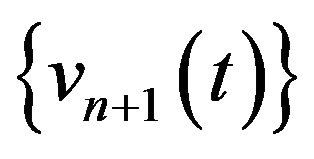 ,
,  ,
,  and
and  are Cauchy sequences in
are Cauchy sequences in  Assume that
Assume that
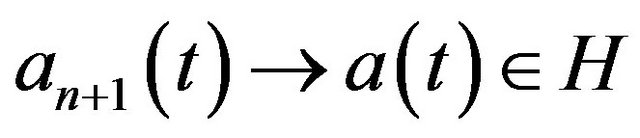 ,
,  ,
,
 ,
,  and
and
 as
as , for each fix
, for each fix .
.
Now by using the random continuity of the random operators ,
,  and Algorithm 1, we have
and Algorithm 1, we have
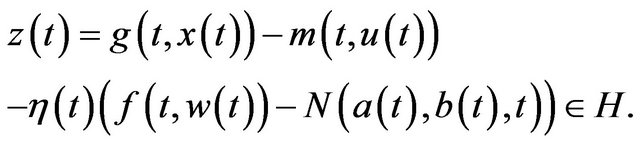
Now we show that  In fact
In fact

where,

Since the random sequences  and
and 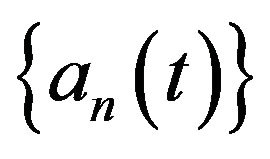 are Cauchy sequences, it follows from the above inequality that
are Cauchy sequences, it follows from the above inequality that . This implies that
. This implies that
 . In a similar way, we can show that
. In a similar way, we can show that
 ,
,  ,
, 
and .
.
By Theorem 1, it follows that ,
,  ,
,
 ,
, 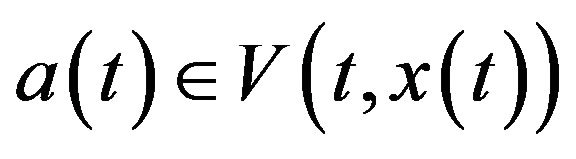 ,
, 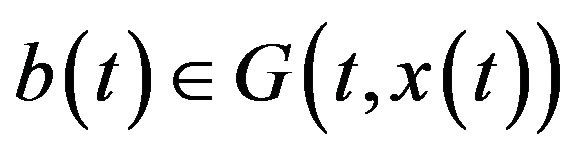 ,
,
 and
and , which satisfies the inequality (1) and for fix
, which satisfies the inequality (1) and for fix ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  and
and 
strongly in  the required result.
the required result.