Server Workload in an M/M/1 Queue with Bulk Arrivals and Special Delays ()
1. Introduction
The M/M/1 arrival/delay mechanism considered in this paper was introduced by Hlynka [1], who derived the Laplace transform of the busy period of the server, using the probabilistic interpretation of the Laplace transform. The busy period in that analysis included the idle times of the server while a secondary is being delayed.
Here we analyze the model using a level crossing approach, and derive: the steady-state pdf of the server workload; probability that the system is empty; probability that the server is idle when a secondary is being delayed; expected busy period (as defined in Hlynka [1]); a stability condition; expected time the server is busy in a cycle between instants of system emptiness, or between instants the server becomes idle and a secondary is being delayed. An advantage of the level crossing method used here is that it focuses on the workload process in a concrete manner. That is, it uses physical properties of a typical sample path of the workload process as a guide, and simple level crossing theorems, to formulate the model equations for the key probability distributions of the model. Viewing the sample path in this concrete manner, makes the solution procedure intuitive, straightforward, and suggestive of future research ideas.
Section 2 specifies the M/M/1 variant and sample path structure. Section 3 derives the model equations for the steady-state pdf of the workload, and specifies related quantities. Section 4 uses the model equations to obtain relevant constant terms, and gives a numerical example of the steady-state pdf of workload.
2. The M/M/1 Variant
Singles (primaries) arrive at the system at Poisson rate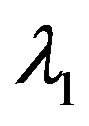 
and pairs (pair = primary + secondary) arrive at the system at Poisson rate
; let
. When a primary arrives at the system, it immediately joins the M/M/1 queue, either alone or just behind a secondary that was being delayed. When a secondary arrives at the system it splits from its primary and is delayed in a separate area outside the queue. The delayed secondary is “pushed” by the next arriving primary to join the queue, followed immediately by the new primary. (Thus the delay of each secondary before joining the queue is distributed as exponential-
.) Customers in the queue are served one at a time at exponential rate 
in firstcome-first-served order. When a primary joins the queue alone, the server workload is increased by exponential-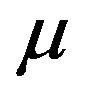
. When a primary and secondary join the queue simultaneously, the server workload is increased by Erlang (2,
), i.e., the sum of two independent exponential-
’s. All secondaries join the queue simultaneously with (next) primaries. The number of secondaries being delayed in the system at any instant is either 0 or 1.
Define the state of the system as 
where W(t) = server workload at time
, 
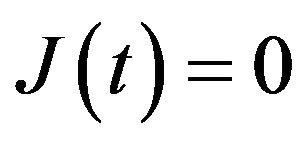if zero secondaries are being delayed, 
if one secondary is being delayed. The state with zero customers in the system is denoted by
. The state when the server is idle and one secondary is being delayed is denoted by
. Let 
denote an exponential-
random variable, and 
denote an Erlang
random variable.
2.1. Sample Path of 
Technique of “Lines and Sheets (or Pages)” We utilize a technique of “lines and sheets (or pages)” to picture the state space and a sample path in it (e.g., see Brill [2] Section 4.6). This technique partitions the state space into mutually exclusive and exhaustive physical lines and sheets corresponding to the states of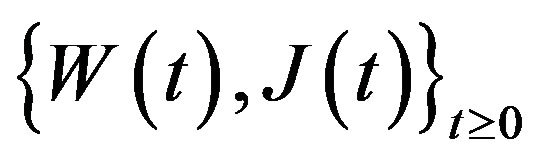
.
We select an arbitrary continuous subset in each sheet, having one boundary as a fixed level 
in the state space of
, e.g., 
,
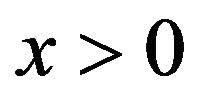. We use this concrete physical picture as a guide to balance the samplepath exit and entrance rates of the selected state-space subsets. Simple level-crossing theorems (e.g., Brill [2]) guarantee that the partial steady-state pdf of 
for each sheet is a unique term, or linear factor in a term, of the corresponding balance equation. The balance equations are generally Volterra integral equations of the second kind with parameter. Thus there is an isomorphism between the physical sample path structure and the model equations.
Consider the sample path of 
in Figure 1. All jumps due to an arrival on page 0 are distributed as 
because only primaries join the queue when arrivals find zero delayed secondaries present. All jumps due to an arrival on page 1 are distributed as 
because both the delayed secondary and the arriving primary join the queue simultaneously.
2.2. Description of the Sample Path of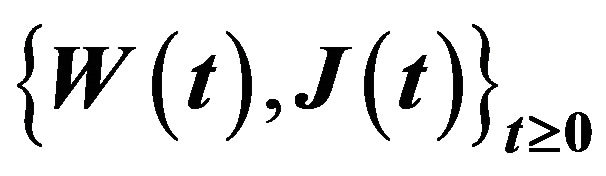 
in Figure 1
At time 0 the system is empty (state
). A single arrives and the SP (sample path) jumps to level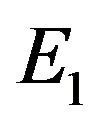 
on page 0; the arrival immediately starts service. The SP decreases at rate 
A pair arrives, the primary joins the queue and the secondary is delayed; the SP jumps 
since the server workload includes only those customers in the queue, and transits to page 1 (delayed secondary present).
A single arrives and pushes the delayed secondary to join the queue; the single joins just after it. The SP jumps 
and transits to page 0 (no delayed secondary present).
A single arrives and joins the queue; the SP jumps 
and remains on page 0. A pair arrives; the primary joins the queue and the split-off secondary becomes delayed. The SP jumps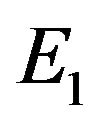 
and transits to page 1. A pair arrives, the primary pushes the delayed secondary into the queue and joins just after it; the new secondary becomes delayed. The SP jumps 
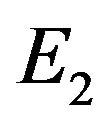and remains on page 1. The SP hits level 0 from above, and remains in state 
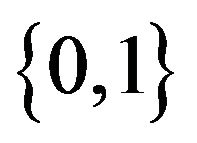for a time distributed as exponentia-
(server idle). A single arrives, pushes the delayed secondary into the queue and follows just after it. The SP jumps by 
and transits to page 0. Finally the SP hits level 0 from above and enters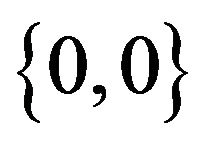 
(system empty).
Figure 1 illustrates a cycle starting and ending in state
. A cycle starting and ending in state 
would be produced similarly.