1. Introduction
Urn models have been among the most popular probabilistic schemes and have received a lot of attention in the literature (see [1,2]). Let us describe the Pólya urn scheme briefly. In 1923, [3] proposed the following urn scheme to model processes such as the spread of infectious diseases. In this scheme, a single urn contains  white balls and
white balls and  black balls. One ball is drawn at random and then replaced, together with
black balls. One ball is drawn at random and then replaced, together with  balls of the same color. The procedure is repeated n times. It is known that the sequence of the proportions of white balls is a martingale converging almost surely to a random variable having a beta distribution with parameters
balls of the same color. The procedure is repeated n times. It is known that the sequence of the proportions of white balls is a martingale converging almost surely to a random variable having a beta distribution with parameters  and
and . Since then, numerous generalizations and extentions of the Pólya urn have been studied : see [4-14]. In 1990, [6] generalized the Pólya urn model with the single change that the number of extra balls added in the urn is a function of time. One ball is drawn and is replaced in the urn along with F(n) balls of the same color. In his setup
. Since then, numerous generalizations and extentions of the Pólya urn have been studied : see [4-14]. In 1990, [6] generalized the Pólya urn model with the single change that the number of extra balls added in the urn is a function of time. One ball is drawn and is replaced in the urn along with F(n) balls of the same color. In his setup  can be any function. He showed that the proportions of white balls converge almost surely and the limit has no atom except possibly at 0 or 1.
can be any function. He showed that the proportions of white balls converge almost surely and the limit has no atom except possibly at 0 or 1.
In this paper, we propose a new class of discrete time stochastic processes generated by a two-color generalized Pólya urn that is reinforced every time. This is a generalization of the urn model considered in [10]. A single urn contains  white balls and
white balls and  black balls: at discrete times
black balls: at discrete times  we draw
we draw 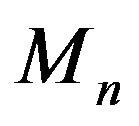 balls and note their colors, say
balls and note their colors, say  are black and
are black and  are white. We return the drawn balls to the urn. Moreover,
are white. We return the drawn balls to the urn. Moreover,  new white balls and
new white balls and 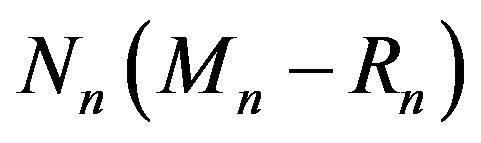 new black balls are added in the urn. The numbers
new black balls are added in the urn. The numbers  and
and  are random variables in
are random variables in . We show that the proportions of white balls form a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to have no atoms at 0 or 1 are given.
. We show that the proportions of white balls form a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to have no atoms at 0 or 1 are given.
This paper is organized as follows. In Section 2, we set the probabilistic model for a randomly reinforced urn. In Section 3, we show that the proportions of white balls form a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to concentrate on the set 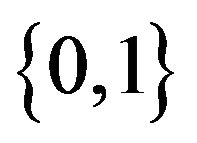 are given. We conclude the paper by proving that interacting reinforced urn process are asymptotically exchangeable.
are given. We conclude the paper by proving that interacting reinforced urn process are asymptotically exchangeable.
2. Model Description and Notation
On a rich enough probability space , define two sequences
, define two sequences  and
and  of positive, integervalued random variables and let
of positive, integervalued random variables and let  and
and  are fixed positive integers. A randomly reinforced urn generates the stochastic processes
are fixed positive integers. A randomly reinforced urn generates the stochastic processes . The sequences
. The sequences 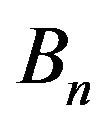 and
and 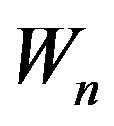 respectively denote the number of black balls and white balls in the urn at time
respectively denote the number of black balls and white balls in the urn at time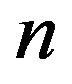 . The dynamics of the processes
. The dynamics of the processes  and
and  are governed by the following: set
are governed by the following: set  and let
and let
 be a
be a 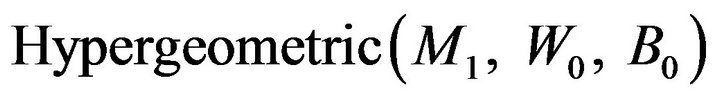 random variable. Now we iterate this sampling scheme forever. Thus, at time
random variable. Now we iterate this sampling scheme forever. Thus, at time , given the sigma-field
, given the sigma-field  generated by
generated by , we consider that
, we consider that 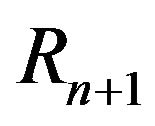 is a Hypergeometric
is a Hypergeometric 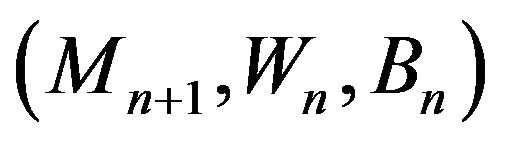 random variable and we assume that
random variable and we assume that 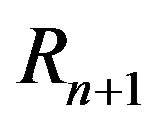 and
and 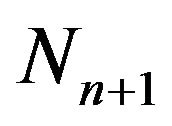 are independent conditionaly on
are independent conditionaly on . Finally, we set
. Finally, we set
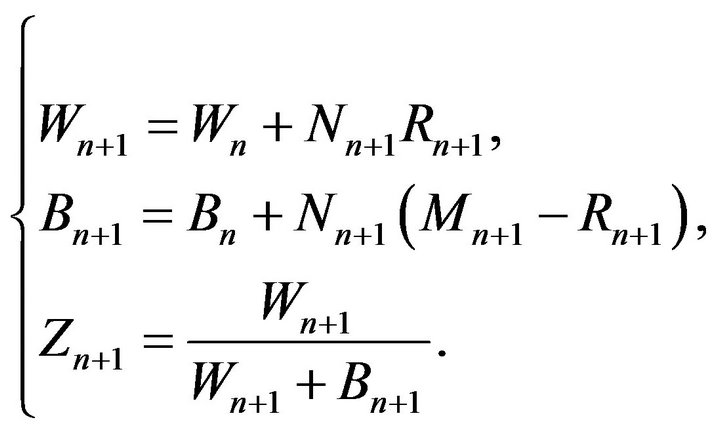 (2.1)
(2.1)
This is a generalization of the reinforced urn model considered in [10]. Assume that, at each time periode  a new firm appears on the market and have to choose operative systems among the systems A and B, for its
a new firm appears on the market and have to choose operative systems among the systems A and B, for its  computers. The firm can choose
computers. The firm can choose  blocks of size
blocks of size  of computers having the operative system
of computers having the operative system . This choice depends on the number of computers having the operative system A on the market. The process
. This choice depends on the number of computers having the operative system A on the market. The process 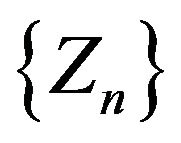 given in (2.1) is going to describe the evolution along time of the proportion of computers operating systems A.
given in (2.1) is going to describe the evolution along time of the proportion of computers operating systems A.
3. Martingale Property
The process  is of primary interest for studying the stochastic processes generated by this generalization of Pólya’s urn. Here
is of primary interest for studying the stochastic processes generated by this generalization of Pólya’s urn. Here  represents the proportion of white balls in the urn at time
represents the proportion of white balls in the urn at time . We show that these proportions form a bounded martingale. This martingale converges almost surely. The next theorem is of fundamental importance, this is our main result.
. We show that these proportions form a bounded martingale. This martingale converges almost surely. The next theorem is of fundamental importance, this is our main result.
Theorem 3.1. The sequence  is a bounded martingale with respect to the filtration
is a bounded martingale with respect to the filtration  taking values in
taking values in  Therefore, it converges almost surely to a random variable
Therefore, it converges almost surely to a random variable 
Proof.
Here  with
with 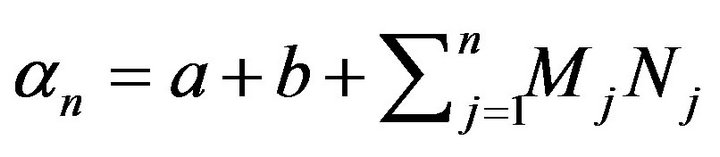 being the total number of balls in the urn at time
being the total number of balls in the urn at time . Now let us show that
. Now let us show that  is a martingale. In fact
is a martingale. In fact
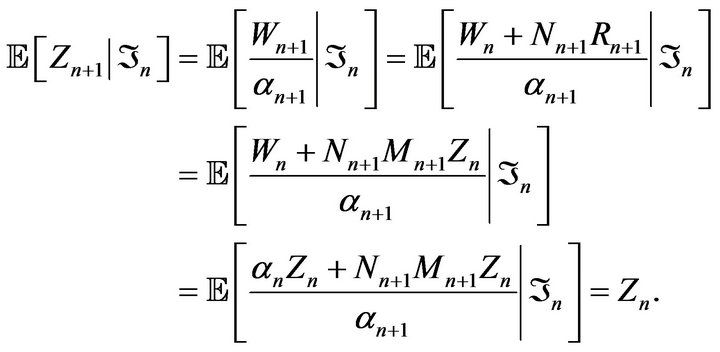
This shows that  is
is  -bounded martingale with respect to the filtration
-bounded martingale with respect to the filtration . Hence, there exists a random variable
. Hence, there exists a random variable 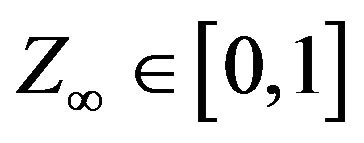 such that
such that 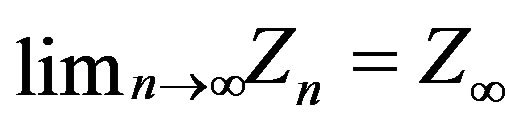 on a set of probability one.
on a set of probability one.
The exact distribution of  is unknown except in a few particular cases. The situation where
is unknown except in a few particular cases. The situation where 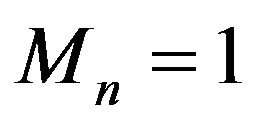 almost surely for all
almost surely for all  and
and  almost surely for all n corresponds to the classical Pólya-Eggenberger contagious urn scheme. In this case
almost surely for all n corresponds to the classical Pólya-Eggenberger contagious urn scheme. In this case  has a beta distribution with parameters
has a beta distribution with parameters  and
and . Let us continue with the general case.
. Let us continue with the general case.
Theorem 3.2. The limit  is Bernoulli distributed if and only if
is Bernoulli distributed if and only if
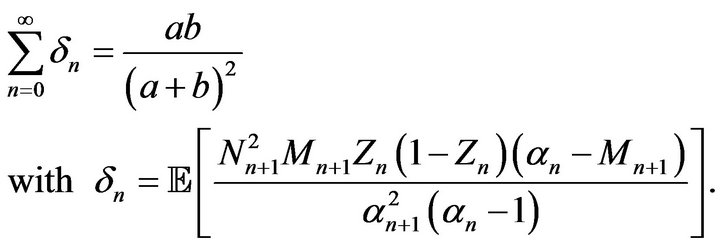
Proof. From (2.1) we have
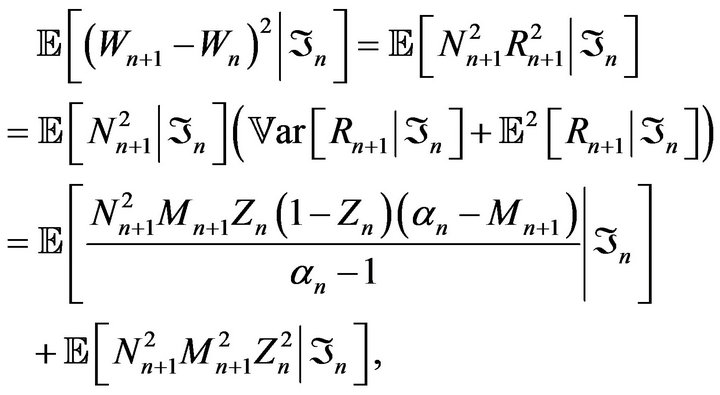
thus we get

The transition between the second equality and the third equality relies on the fact that, conditionally on  are independent. As a result
are independent. As a result
 , (3.1)
, (3.1)
with 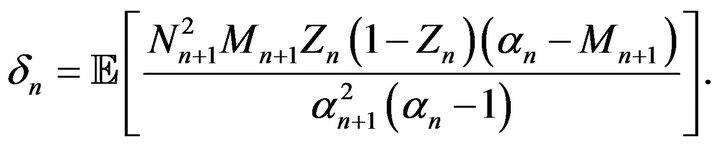
Now we set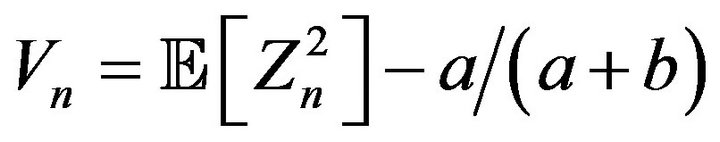 , and we have from (3.1)
, and we have from (3.1)

Consequently, 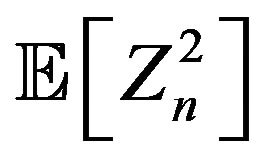 converges to
converges to 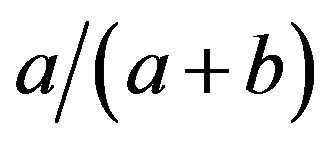 if and only if Vn converges to
if and only if Vn converges to , which happens whenever
, which happens whenever
 . This is the desired result because a random variable
. This is the desired result because a random variable  satisfies the condition
satisfies the condition
 if and only if
if and only if  is concentrated on the set
is concentrated on the set .
.
This theorem applies, for example, when 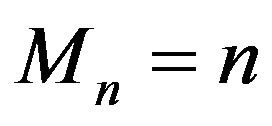 and
and  almost surely. In fact from (3.1), we remark that when
almost surely. In fact from (3.1), we remark that when  and
and 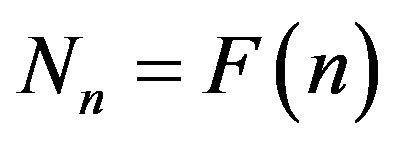 almost surely (
almost surely ( and
and 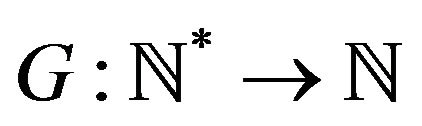 be any function) we have
be any function) we have

and we deduce
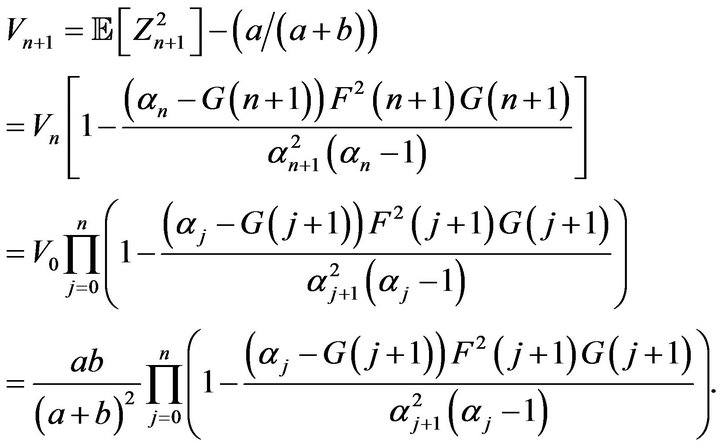
Consequently,  converges to
converges to  if and only if
if and only if  converges to
converges to , which happens whenever the product values
, which happens whenever the product values
 converges to
converges to
 . This happens whenever
. This happens whenever
 diverges.
diverges.
Moreover, if  and
and  then
then
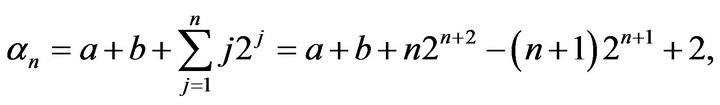
the general term of the series being proportional to .
.
From Theorem 3.1 we deduce thatCorollary 3.3. Assume that the sequence  satisfies the following conditions
satisfies the following conditions

then
and

Proof. For every fixed  and for sufficiently large
and for sufficiently large ,
,
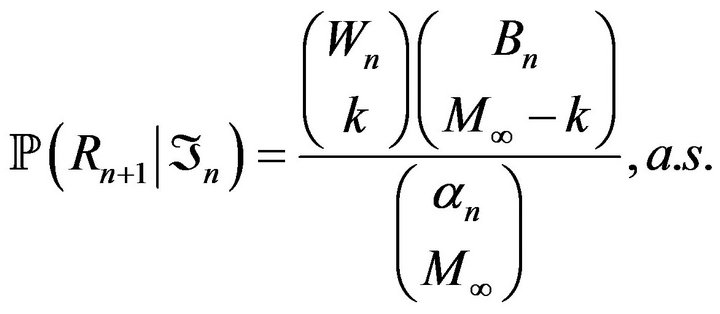
Then, using the well know convergence of the hypergeometric probabilities to the binomial, we have

and the conclusion follows from the bounded convergence theorem.
As a consequence of Theorem (3.2), we have the following.
Corollary 3.4. Assume that the sequences  and
and  are bounded then
are bounded then 
Proof. Since the sequences  and
and  are bounded by some constant
are bounded by some constant 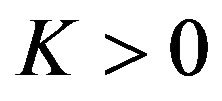 and for all
and for all 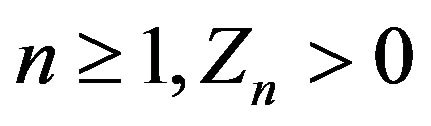 we obtain from (3.1) that
we obtain from (3.1) that
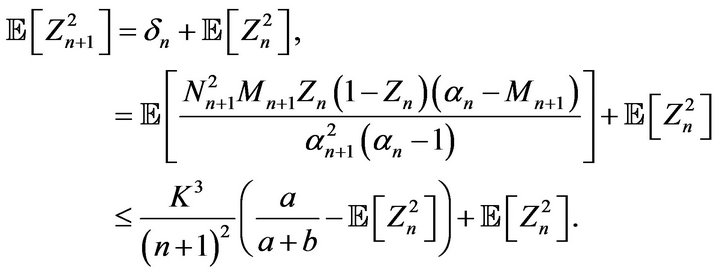
Let 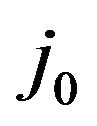 be such that
be such that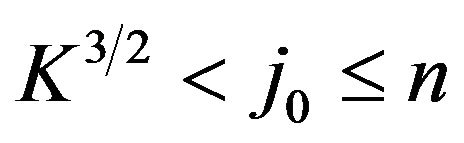 . We obtain that
. We obtain that

Now, since , then
, then
 and
and 
so 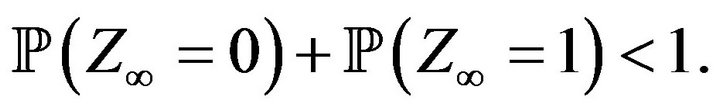
The final result in this section shows that the law of large numbers holds for interacting reinforced urn systems.
Theorem 3.5. We have
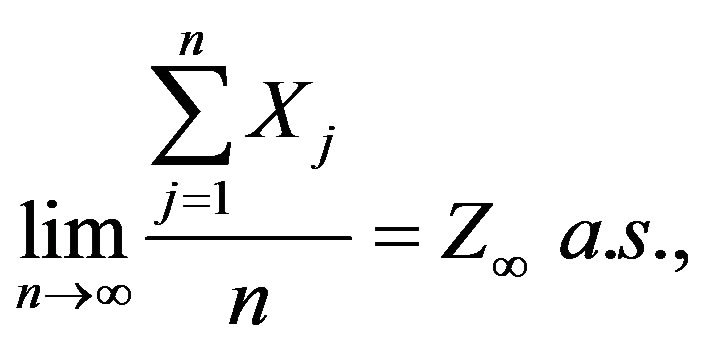
with 
Proof. Using Cesàro’s summability result we obtain that,

Let . Since
. Since  then we have the following1)
then we have the following1) , for all
, for all .
.
2) For all  we have
we have

This shows that the sequence  is orthogonal, with zero mean.
is orthogonal, with zero mean.
3) For , we have
, we have
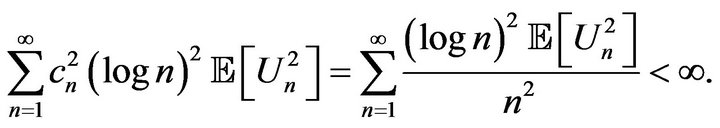
Therefore, the sequence  satisfies the conditions of Hall’s theorem (see [15], Theorem 2.8, p. 22), and we can conclude that the series
satisfies the conditions of Hall’s theorem (see [15], Theorem 2.8, p. 22), and we can conclude that the series
 (3.2)
(3.2)
Finally, Kronecker’s lemma yields
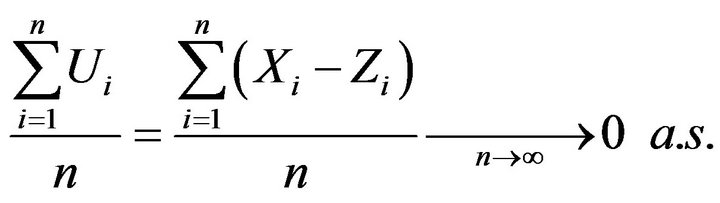 (3.3)
(3.3)
This shows that
 (3.4)
(3.4)
which is the announced result.
4. Asymptotic Exchangeability
According to [16] a sequence of random variables  is asymptotically exchangeable if the joint distribution of the sequence
is asymptotically exchangeable if the joint distribution of the sequence  converges as
converges as  to the distribution of some exchangeable sequence
to the distribution of some exchangeable sequence . In particular, we have the following lemma due to [17].
. In particular, we have the following lemma due to [17].
Lemma 6. (Aldous)
Consider  be an infinite exchangeable sequence directed by
be an infinite exchangeable sequence directed by .
.
1) Let  be a regular conditional distribution for
be a regular conditional distribution for  given
given .
.
Then
 (4.1)
(4.1)
2) Let  be an infinite sequence. Let
be an infinite sequence. Let  be a regular conditinal distribution for
be a regular conditinal distribution for  given
given , and suppose that
, and suppose that 
Then
 (4.2)
(4.2)
Theorem 3.1 together with Lemma yield that the sequence of random variables 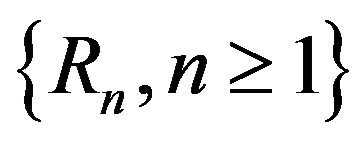 is asymptotically exchangeable. The main result of this section is the following.
is asymptotically exchangeable. The main result of this section is the following.
Theorem 4.1. Under the conditions of Corollary 3.3, the sequence of random variables  is asymptotically exchangeable.
is asymptotically exchangeable.
Proof. For all , the conditional distribution of
, the conditional distribution of  given
given , is such that
, is such that
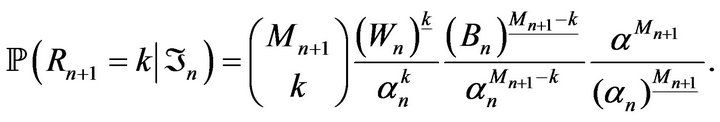
Hence, as in Corollary 3.3, we obtain that

The conclusion comes from Lemma 4.1, part (b).
5. Conclusions
Urn model have been widely studied and applied in both scientific and social science disciplines. In this paper, we have proposed a general class of discrete stochastic processes generated by a two-color generalized Pólya urn. This model generalizes a model previously studied by [10]. This paper also shows that the proportion of white balls form a bounded martingale sequence which converge almost surely. Asymptotic properties and asymptotic exchangeability are given. However, the complete characterization of the limit still remains to be resolved in the future and it would be interesting to explore the possibility extensions to more than two colors.
Another important application of this urn models is to randomize treatments to patients in a clinical trial (see [18]). Consider an urn containing balls of two type, representing two treatements. Patients normally arrive sequentially, and treatment assigned on the urn composition and previous treatment outcomes. For more details analysis on this application, we refer to [13].
6. Acknowledgements
The authors want to thank Professor Éric Marchand for his numerous advices and helpful discussions. The second author wants to thank NSERC for the financial support.
NOTES