Influence of volatile degassing on initial flow structure and entrainment during undersea volcanic fire fountaining eruptions ()
1. INTRODUCTION
Interpreting the processes of submarine explosive eruptions has been difficult owing to the rarity of direct observations. Geological evidence suggests that submarine fire fountaining takes place in the marine environment based on the occurrence of fluidal breccias and highly vesicular basaltic clasts that show similarities to their subaerial counterparts [1] . Head and Wilson [2] have presented a comprehensive treatment of the theoretical considerations of submarine fire fountaining by exsolution of primary volatiles (CO2 and H2O). In their model they assume that fragmentation occurs when a gas volume fraction of 0.75 is attained by gas exsolution either within the conduit or right at the vent. An intriguing problem concerning submarine fire fountaining is to verify whether or not such an assumption is always valid. In subaerial eruptions, fragmentation typically occurs within the conduit or vent [3] . However, in the marine environment the hydrostatic pressure may be sufficient to inhibit bubble fragmentation until the magma has been discharged at the sea floor and rises to a depth where pressure is sufficiently reduced. This presents a potentially interesting phenomenon where a bubbly magma is erupted prior to fragmentation, but is buoyant relative to seawater, a condition that can never occur in the subaerial environment. If film boiling conditions sufficiently inhibit heat transfer, the flow structure may behave as an immiscible jet, plume or fountain. Subsequent mingling between discharged magma and seawater may provide an additional fragmentation trigger as a result of phreatomagmatic explosions and fundamentally control the nature of the subsequent eruption [4,5]. In this paper, we analyze the conditions that lead to positively buoyant discharges of vesiculated magma in submarine environments and discuss the potential implications for the entrainment of seawater and eruptive behavior based on some analogue experiments. We find that the initial flow structure of submarine eruptions is likely to vary significantly with water depth owing to the changes in buoyancy flux associated with the release of dissolved volatiles.
2. BACKGROUND
2.1. Magma Buoyancy and Fragmentation
Subaerial fire fountains consist of a spray of hot fluidal clasts and gas ejected at velocities up to about a hundred meters/s forming spectacular fountains a few tens to several hundred meters above the vent [6] . The majority of clasts fall quickly back to the surface because a strong buoyantly convective phase is never fully developed and the fragmentation of clasts is relatively inefficient [7] . Accumulation of hot, fluidal clasts around the vent area produces distinctive spatter deposits that are characteristic of this type of activity. We suggest that complex behaviors of fire fountaining are possible in the submarine environment that would not occur under subaerial conditions. Such behaviors are related to the potential for having a positive buoyancy flux at the source vent of submarine basaltic fire fountaining eruptions.
Subaqueous eruptions of vesiculating magma will be positively buoyant if the bulk magma density 
is less than that of the surrounding seawater
. The bulk density is a function of the mass fraction of exsolved volatiles 
(the mass fraction of volatiles that have separated from the solution), density of the exsolved volatile 
and the dense rock density
.
where 
depends on the total volatile mass fraction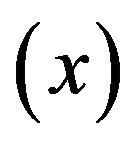 
and the solubility of the volatile component in the magma
,
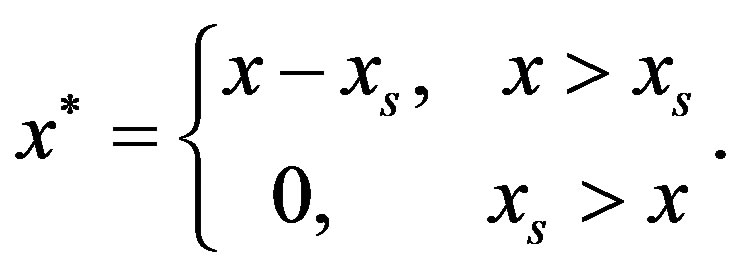
The soluble limit for a given volatile component and magma composition is a function of pressure and temperature
.
We have evaluated conditions of magma buoyancy using the VolatileCalc 1 program to calculate gas solubilities [8] . For CO2, the density was calculated using the ideal gas law and in the case of water, the density of the exsolved component (steam) was taken from tabulated data (ASME Steam tables). As a result of surface tension
, the pressure within a gas bubble exceeds the pressure of the surrounding fluid
,
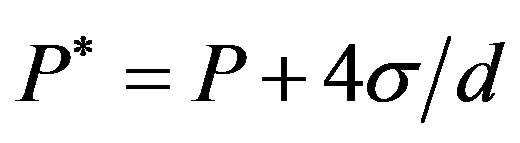
where d is the void diameter. For non-spherical bubbles the diameter is calculated from a major and minor axis,
. For simplicity in our calculations we have assumed that the pressure in the bubbles is equal to that of the ambient pressure and ignored this surface tension effect, which requires a detailed knowledge of bubble size and the complex interfacial tension relationship.
Bubbly suspensions of uniformly sized bubbles can commonly exist up to a gas volume fraction of 0.85 before fragmentation [9] and a fragmentation limit of about 0.75 is often cited based on observations of natural subaerial samples [10-12]. However, recent experimental work has identified a critical overpressure necessary to fragment magma that is a function of porosity and permeability [13,14]. Fragmentation can occur at gas volumes significantly below 0.75, but requires relatively high levels of overpressure, especially if the magma has high permeability. At exsolved gas volumes of 0.75 a critical overpressure of about 2 - 3 MPa is required to fragment magma into low pressure atmospheric conditions. This required overpressure is likely the result of the tensile strength of the melt phase and the interfacial tension noted above. In submarine eruptions the presence of hydrostatic pressure at the vent should inhibit magma fragmentation relative to subaerial eruptions. For example, the ambient pressure at only 200 m water depth is 2 MPa, or similar to the required overpressure necessary to fragment magma with gas volume fraction of 0.75. In our calculations we have used the 0.75 fragmentation limit with the caveat that this limit may potentially be higher in submarine events.
Simple degassing calculations using the equations cited above demonstrate that it is possible for basaltic magma that is vesiculating to attain positive buoyancy relative to seawater prior to reaching gas volume fractions commonly associated with fragmentation (75%). Figure 1 shows the vesicularity for a 1200˚C basaltic magma as a function of water content and depth. The dashed line “Positive Buoyancy” is the minimum vesicularity required to have a net upward buoyant force on the magma. The slight positive slope of this line results from the density increase of the volatile phase with increasing water depth. The solid line assumes that fragmentation occurs at 75% vesicularity. Thus the band between these two lines represents a zone of positively buoyant unfragmented magma. Consider 1200˚C basaltic magma with a 2% water content. At a depth of 1000 meters it would be positively buoyant, but would not reach the fragmentation point until a depth of 700 m. The results indicate that magmas with higher volatile contents have a larger depth range over which they are buoyant but still not at the fragmentation threshold. Unfragmented magma with 4% water, for example, could exist at depths of 1600 to 2500 meters.
The range of volatile contents that we evaluated in Figure 1 (1% - 4%) is higher than most juvenile water contents associated with basaltic magmas [15] . However, recent discoveries of deep water basaltic explosive volcanism has led to the suggestion that pre-concentration of volatiles prior to eruption may be an important process in driving gas contents high enough to support explosive
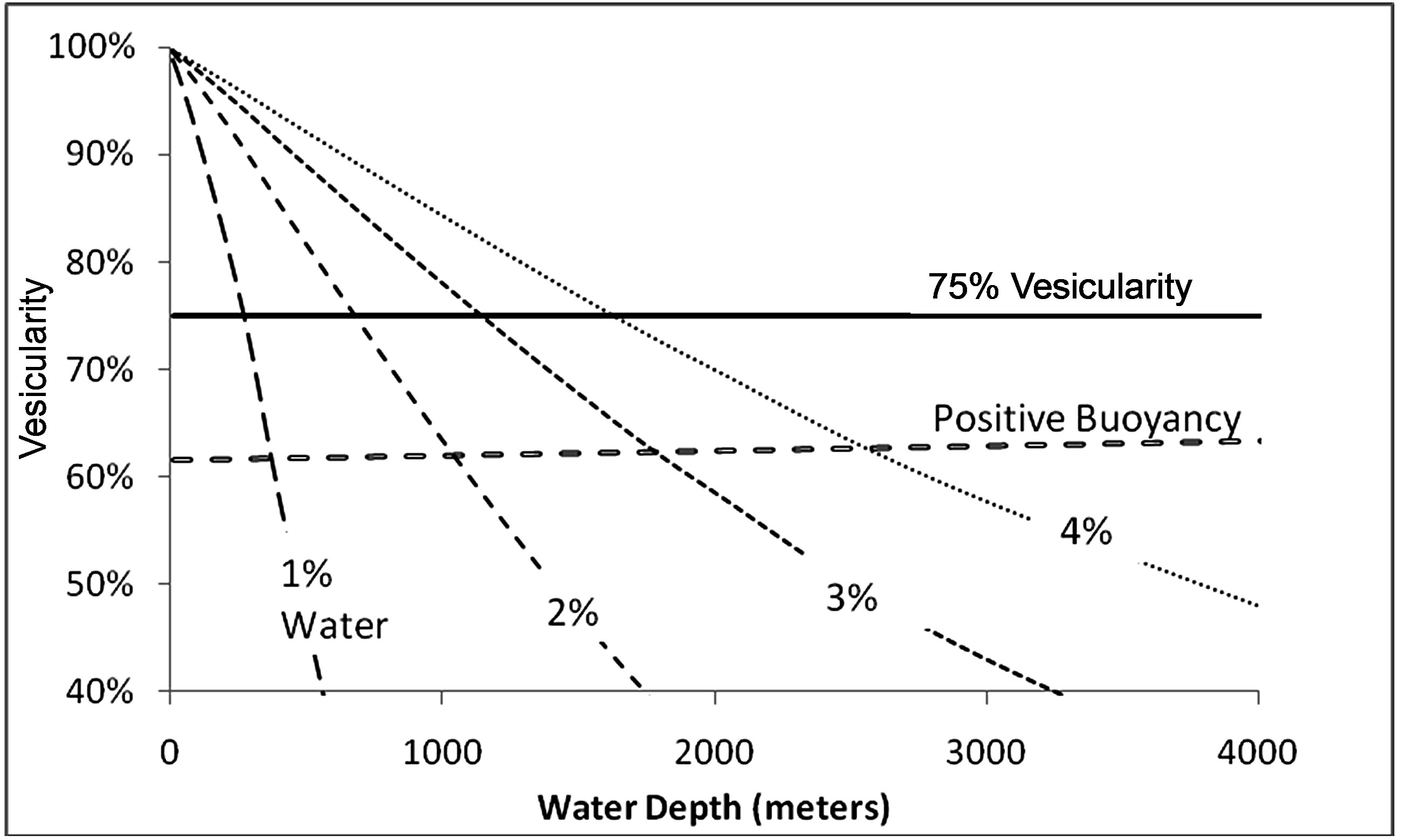
Figure 1. Variation in the vesicularity of magmas with volatile contents from 1% to 4% water as a function of water depth for 1200˚C magma. The typical fragmentation vesicularity of 75% is shown along with the vesicularity value where magma above which magma is buoyant relative to seawater. The positive buoyancy vesicularity increases slightly with depth as the result of an increasing density of the gas phase at higher pressures.
fragmentation in the submarine environment [2,16]. Thus submarine fire fountaining may be driven by volatile contents higher than those typically associated with the primary gas content of seafloor basalts.
2.2. Hydrodynamic Background
Subaqueous eruption of magma differs significantly from subaerial conditions owing to the difference in density of the ambient environment into which magma is discharged and the dramatic variations in the rate of heat exchange between magma and water versus magma and air. Under film boiling conditions, an insulating vapor blanket develops between molten magma and surrounding seawater, greatly suppressing heat transfer. As a result, a reasonable first order approximation is to analyze the hydrodynamic flow structure as decoupled from heat transfer until fragmentation occurs. A vertically-directed immiscible discharge is governed by the functional relationship [17] :
where:
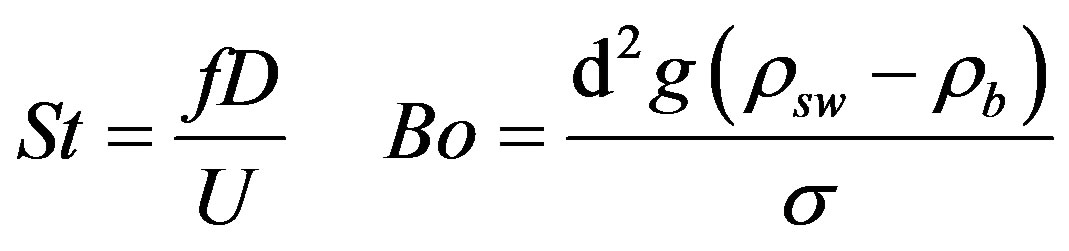
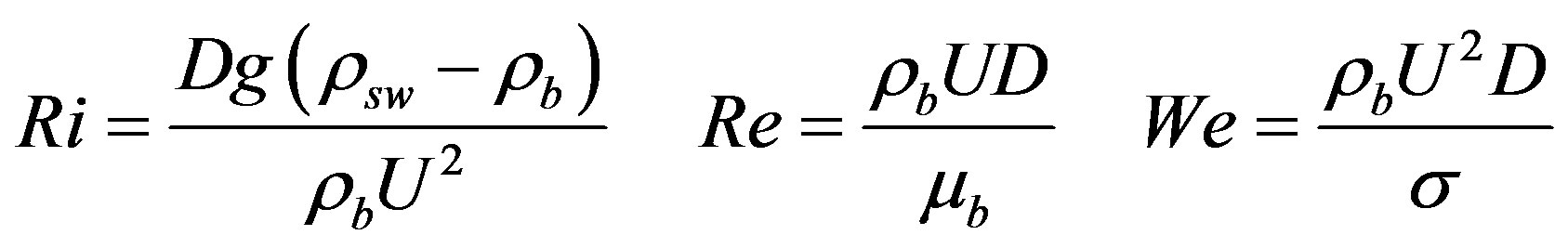
Here, D is the vent diameter; U is the vent exit velocity; h is the characteristic height in flow structure;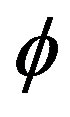 
is the vent geometry parameter; d is the characteristic mingling void size; 
are the bulk and ambient viscosities, respectively; 
is the interfacial tension between discharged and ambient fluids and f is the characteristic frequency of the flow structure.
The dependent Strouhal number 
represents a dimensionless characteristic frequency of the flow structure. In the case of a negatively buoyant fountain, St is the frequency at which the fountain collapses and reforms [18] . The Bond number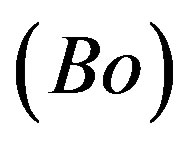 
is the dimensionless size of the mingling between the phases [19] and 
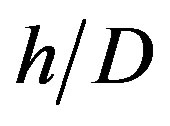is the dimensionless characteristic height of the flow structure. In the case of a negatively buoyant fountain or jet, 
is the maximum height of rise of the flow structure [20]. The independent Richardson number 
is the ratio of the buoyant forces to the inertial forces1. As will be discussed below, Ri is the dominant parameter in determining the flow structure. Reynolds number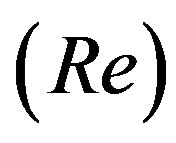 
is the ratio of the inertial to the viscous forces. Weber number 
is the ratio of the inertial forces to the interfacial tension forces of the overall vent structure. In the case of volcanic eruptions,
. The other independent parameters are a discharge vent shape parameter and the viscosity ratio between the discharged and ambient fluid. The bulk viscosity of the magma is dependent on the Capillary number of the magma [21] . In general, at high capillary numbers 
where viscous forces dominate, the viscosity decreases with increasing vesicularity.
3. LABORATORY EXPERIMENTS
Our analysis of submarine eruption processes draws on experimental results performed on negatively buoyant fountains and jets that were previously reported in [17,18] and additional experiments conducted on positively buoyant jets and plumes. The equipment and procedures, which are briefly described here, are more thoroughly discussed in [17,18]. The experimental setup (Figure 2) consisted of a 30.5 (L) × 30.5 (W) × 40 cm (H) test chamber, a circulating pump loop and an illumination and data acquisition system. The circulating loop drew the fountain fluid from a reservoir at the bottom or top of the test facility, depending on whether negatively or positively buoyant cases were being investigated and pumped it through a throttle valve and flow meter to the vent assembly in the test chamber. Vent geometries included a convergent nozzle, cylindrical pipes with diameters ranging from 1.9 cm to 3.8 cm and a rectangular geometry. The facility was illuminated using the beam of a New Wave Research dual-head, Solo 30 PIV Nd:YAG passed through a pair of cylindrical lenses that form a light sheet and a spherical lens that controlled the light sheet thickness. Digital images were captured using a TSI Model# 630057 PowerView plus 2 Megapixel digital CCD camera. When permitted by index matching [17] and fluid clarity, the fluid flow structure was analyzed using TSI Insight 6 particle image velocimetry (PIV) Software.
Sample images for positively and negatively buoyant discharges are shown in Figure 3. A negatively buoyant fountain occurs when negative buoyancy dominates (nominally
). The flow structure is characterized by stable smooth flow structure without phase mingling. As inertial forces are increased (nominally
) a negatively buoyant jet develops and the rise height increases to the point where an unsteady flow structure repeatedly collapses and reforms. Positively buoyant jets 
are dominated by inertia, whereas plumes are dominated by positive buoyancy. Oscillating plumes narrow as buoyancy accelerates the flow, which subsequently develops a sinusoidal shape that oscillates in a radial pattern and then breaks apart. Blob plumes break apart at the vent with a characteristic dimension on the order of the size of the vent. Finally atomized plumes break immediately apart with a characteristic dimension that is small in comparison to the vent diameter.
In the case of negatively buoyant eruptions, Ri is overwhelmingly the dominant independent parameter of Eq.1 with specific flow behaviors associated with certain threshold values [18] . For Ri < –1.0, a smooth stable fountain forms; while for negative Richardson numbers above this threshold, a distinct transition occurs in which an unstable negatively buoyant jet alternately collapses and reforms [18] . This instability causes phase mingling. The nominal Ri = –1 transitional Richardson number is slightly altered by varying Reynolds number
, Weber number 
and viscosity ratio [17] . Most of the Re effect can be accounted for by defining a corrected Richardson number 
in terms of a root mean
Figure 2. Experimental setup. For positively buoyant experiments, suction was drawn from above the interface.
Figure 3. Experimentally recorded images of the flow structures for positively and negatively buoyant fountains, jets and plumes. Silicone oil is used for the lighter fluid and a glycerin/water mixture that is mixed in proportion.
square average velocity to account for the increased momentum of laminar flows. Interfacial surface tension stabilizes the interface and leads to a trend of decreasing transitional 
with increasing 
(corrected Weber number defined similarly to
). Although the effect is relatively minor, viscosity ratios deviating from unity stabilize the interface leading to a trend of a minimum transitional 
for viscosity ratios of 1.0. Results for noncircular vents are consistent with the data for cylindrical exits if flow parameters are defined in terms of the hydraulic diameter.
The positively buoyant images shown in Figure 3 are illustrative of the types of potential flow structures from preliminary experiments that were performed without individually controlling for the effects of Re, Viscosity ratios, and We. Despite this limitation the results point to a variety of complex flow structures in which the two fluids exhibit enhanced mingling relative to the negatively buoyant collapsing fountains. Such mingling is likely critical to achieving the necessary pre-mixing conditions for phreatomagmatic interactions that could provide a positive feedback to fragmentation associated with primary volatile degassing [22] .
While the experimental results demonstrate that the Richardson number is the dominant parameter (with Reynolds number, viscosity ratio and Weber number providing relatively minor contributions in the range of parameters investigated), it is impossible to match the broad range of viscosity ratios and Reynolds numbers that potentially occur in actual eruptions. The viscosity of basaltic magma can range from 102 to 104 poise. In addition, the bulk viscosity can vary greatly as a result of entrained bubbles, depending on the Capillary number [23] .
4. NUMERICAL SIMULATIONS
In order to further investigate the nature of potential submarine flow structures we used an in-house flow solver called NGA [24-26] to perform numerical simulations of positively buoyant discharges. NGA is designed for simulations of turbulent multiphase flows. Using a consistent mass and momentum transport scheme [27] , NGA can handle simulations of multiphase flows with arbitrary large density ratios. NGA solves turbulent flows using either direct numerical simulation (DNS) or large eddy simulation (LES) approaches and has been carefully validated [24-27] using several canonical test cases.
The governing equations for a multiphase flow of Newtonian immiscible fluids are conservation of mass and momentum
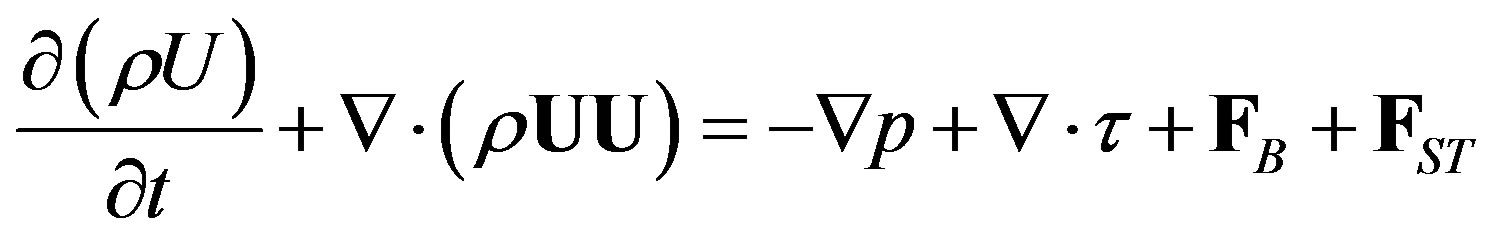
where U denotes velocity, p pressure, τ the shear stress tensor
, FB body force (e.g. gravity), and FST is the surface tension force.
NGA is a parallel, finite-difference, structured, flow solver with staggered arrangement of variables. It employs the projection method to solve the governing equations in which the temporal integration is done using an iterative, second-order, Crank-Nicolson formulation. A single set of governing equations is solved in the whole numerical domain for simulations of multiphase flows, where the spatial terms are discretized with second-order accurate schemes. At any point in the domain, the fluid properties, namely density ρ and viscosity μ are determined by a scalar indicator function G (described below). To incorporate jump conditions across fluid interfaces, the Ghost Fluid method (GFM) [25,28] is employed.
To model the kinematics and deformation of fluid interfaces, a special type of the level set method, known as the spectrally refined interface (SRI) method [26] is used. As demonstrated by Desjardins & Pitsch [26] , SRI exhibits excellent accuracy in modeling complex interface kinematics as well as mass-conservative properties. In this method, the following transport equation for a scalar indicator function 
is solved using a semiLagrangian approach [26] :
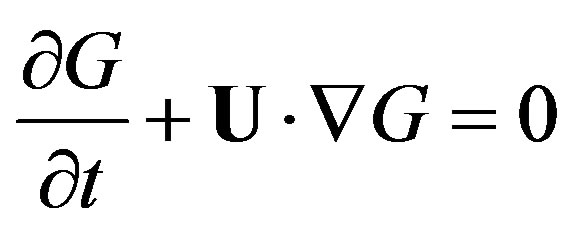
Although G can be any smooth function, we use a signed distance function here, so the interface is represented by an iso-surface G0 = 0.
Figure 4 shows the results of numerical simulations of positively buoyant discharges at two Richardson numbers Ri = 1 and 10. There are 80 grid points across the jet thickness. Comparing to the experimental results (Figure 3), we see that the key features are captured very well in our preliminary simulations. As the figure shows, at low Richardson numbers Ri = 1, the jet is inertia driven and rollups and skirts are formed as the jet rises because of shear force exerted by the surrounding fluid. Increasing the Richardson number to Ri = 10 forms an oscillating jet/plume similar to the experimental result shown in Figure 3, where the breakup now occurs closer to the vent exit.
5. GEOLOGIC ANALYSIS
Here we consider the effects of water depth on the po-
Figure 4. 2D numerical simulation of positively buoyant discharges at Richardson numbers 1 and 10.
tential style of submarine basaltic fire fountaining eruptions as a result of its influence on the bulk density of the initial erupting mixture (degassing). As a baseline eruption, we have chosen a discharge rate of 200 m3/s of dense rock equivalent similar to magma discharge associated with subaerial fire fountaining events [29] . Additionally, the baseline eruption assumes 1200˚C magma, containing 2% water content, with discharge from a 10 meter circular vent. Assuming fragmentation occurs at 75% vesicularity, the discharge would consist of a twophase liquid with suspended bubbles at a depth greater than 700 meters and a two-phase gas with suspended liquid at shallower depths (Figure 1).
As shown in Figure 5, at very shallow conditions (10 meters), the bulk density is 18.4 kg/m3, yielding a Richardson number of 0.03 and these conditions would favor energetic fragmentation by volatile degassing. As depth is increased, the reduction in specific volume of the gas phase causes a decrease in velocity and buoyancy. Initially, the dominate effect is the velocity reduction causing the Richardson number to increase. In the baseline case, buoyancy does not increase sufficiently for a transition to plume behavior. The maximum Richardson number is reached at 500 meters, below which the dominant effect on increasing depth is a reduction in buoyancy. At a depth of 1000 meters, the flow becomes negatively buoyant and the flow structure transitions into a negatively buoyant jet. At a depth of 1400 m, Ri < –1 and the flow transitions to a stable collapsing fountain. Figure 5 also shows the effect of varying water concentration from 0% to 4%. With no volatile constituents, the resultant Richardson number would be –9.2 (the dashed horizontal line), regardless of depth, indicating a stable fountain without phase mingling. With higher discharge rates, the volatile-free line moves upward making mingling possible, even without the presence of volatiles [18] . Each of the curves representing various concentrations of water turns abruptly horizontal at the depth that it reaches the zero volatiles horizontal line. As the concentration of exsolved volatiles increases at shallow depths, the velocity increases resulting in a reduction of Richardson number. An increasing concentration of volatiles increases the depth at which phase mingling can be expected. With 4% water, the fragmentation vesicularity (75%) would occur at a depth of 1400 meters. Positive buoyancy would exist down to a depth of 2200 meters and the mingling threshold of Ri = –1.0 would occur at a depth of about 3500 meters. In comparison to water, CO2 has a much lower increase in solubility with pressure, leading to shallower slopes of the Richardson number curves (Figure 6). Temperature changes of the magma have a slight effect by changing the buoyancy (not shown).
Vent diameter and flow rate have no effect on the tran-
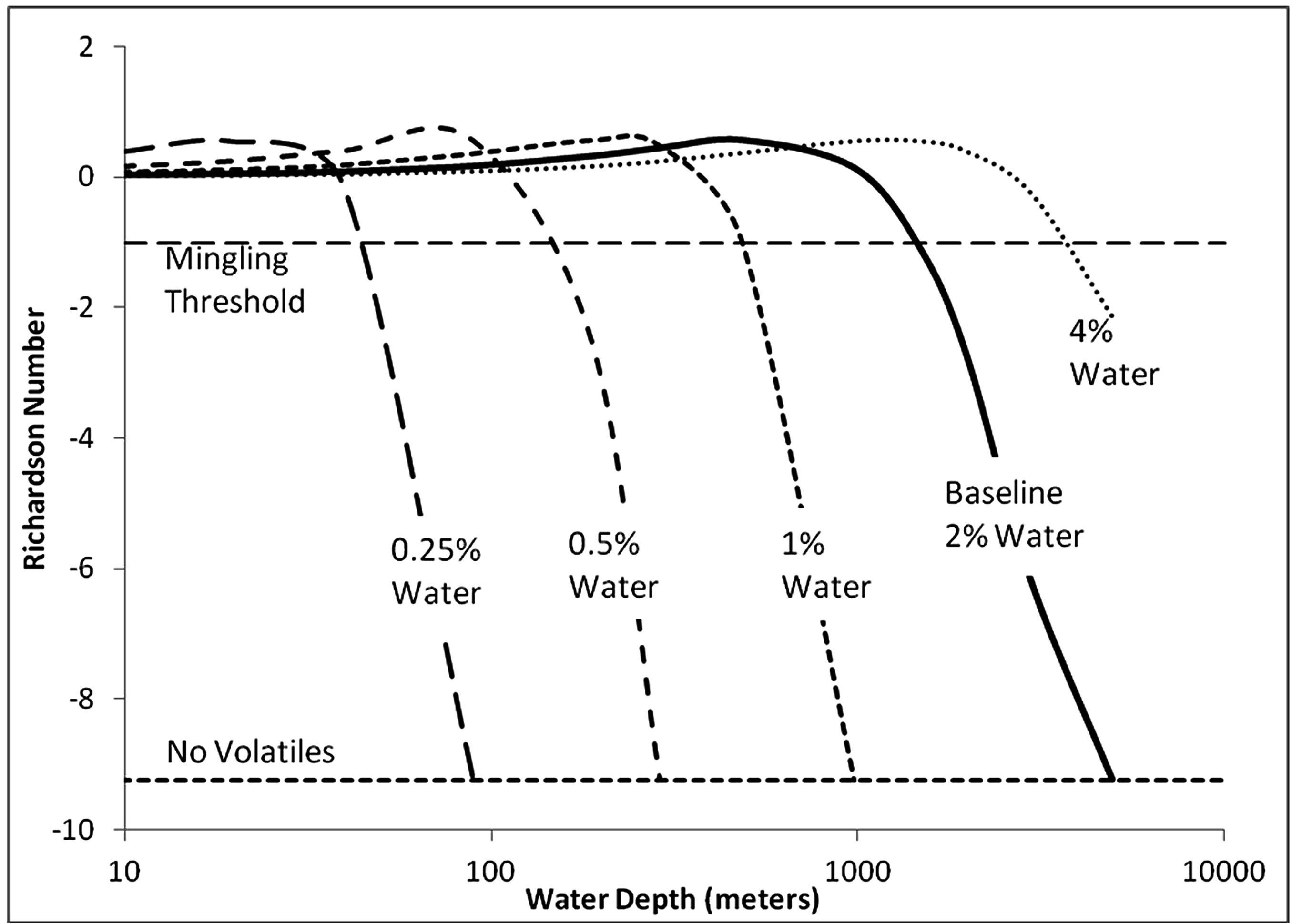
Figure 5. Effect of volatile concentration on Richardson number as a function of water depth. The baseline event is an eruption of 200 cubic meter/s of dense rock equivalent, containing 2% water content at 1200˚C discharging from a 10 meter vent. Under volatilefree conditions, the Richardson number is independent of depth of the vent as seen by the curve labeled “No Volatiles”. Where the each of the curves intersect the no volatiles curve, the pressure is sufficient to hold all volatiles in solution. The curves all bend sharply bend sharply to the right at this point.
Figure 6. Effect of CO2 on Richardson number. At shallow depths, the effect if CO2 is comparable to water. However as pressure increases, the increased solubility of water diminishes its effect.
sition from positive to negative buoyancy (the sign of Ri), but greatly affect the magnitude (Figures 7 and 8). As previously shown, the baseline case never behaves as a plume as a result of the high inertial forces. A reduction in flow rate to 50 cm/s results in a flow that has little chance of mingling at depths in which it is negatively buoyant and it behaves as a plume at most depths in which it is positively buoyant, excepting very shallow eruptions (less than about 20 meters). Likewise increasing the vent diameter has a similar effect.
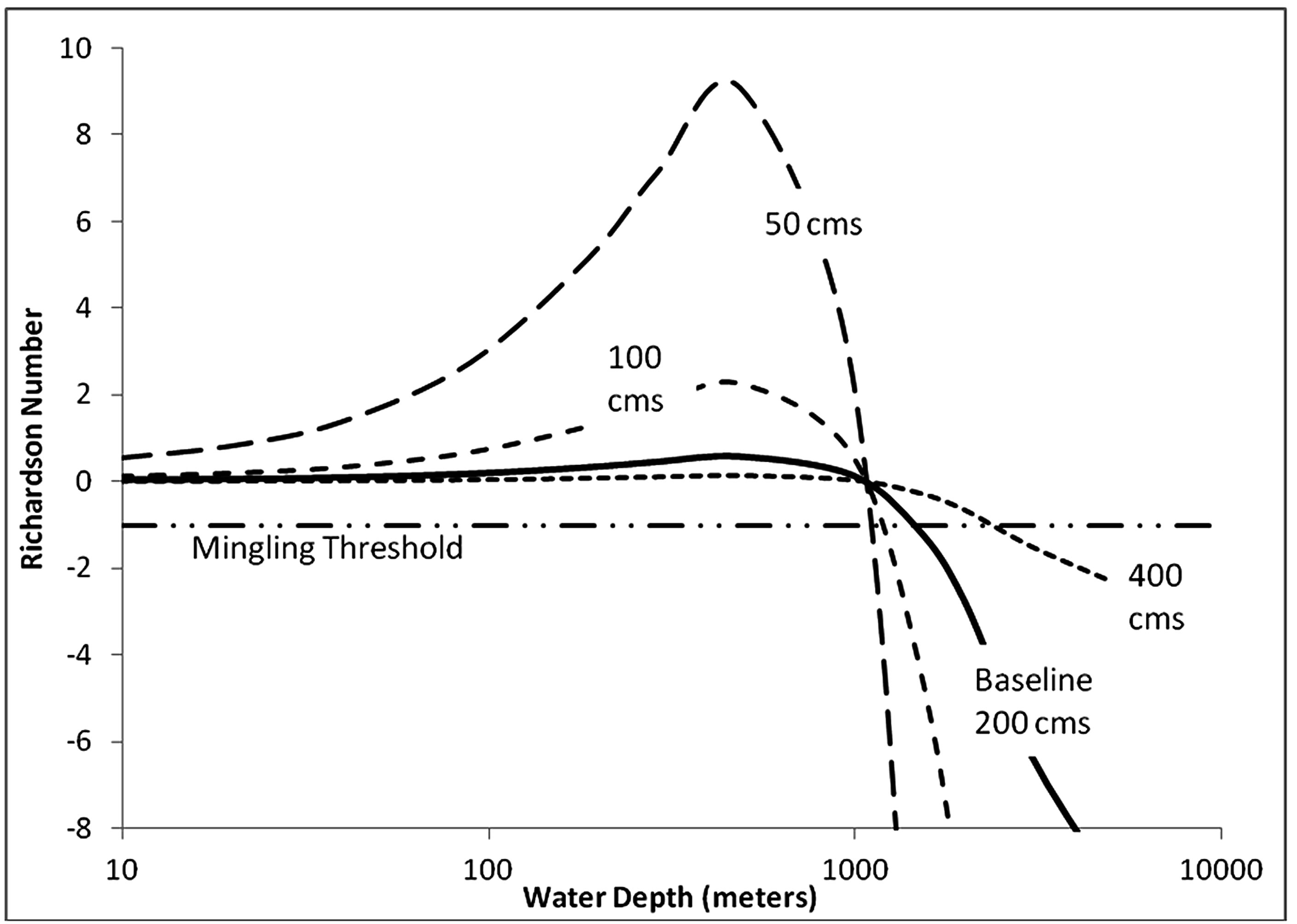
Figure 7. Effect of flow rate, indicated in cubic meters per second (cms), on Richardson number. The flow rate has no effect on the depth at which the flow becomes positively buoyant (Ri = 0); however, increasing flow rate increases the inertia and causes absolute value of all Richardson numbers to decrease. As the flow rate increases, the depth at which phase mingling potentially occurs increases.
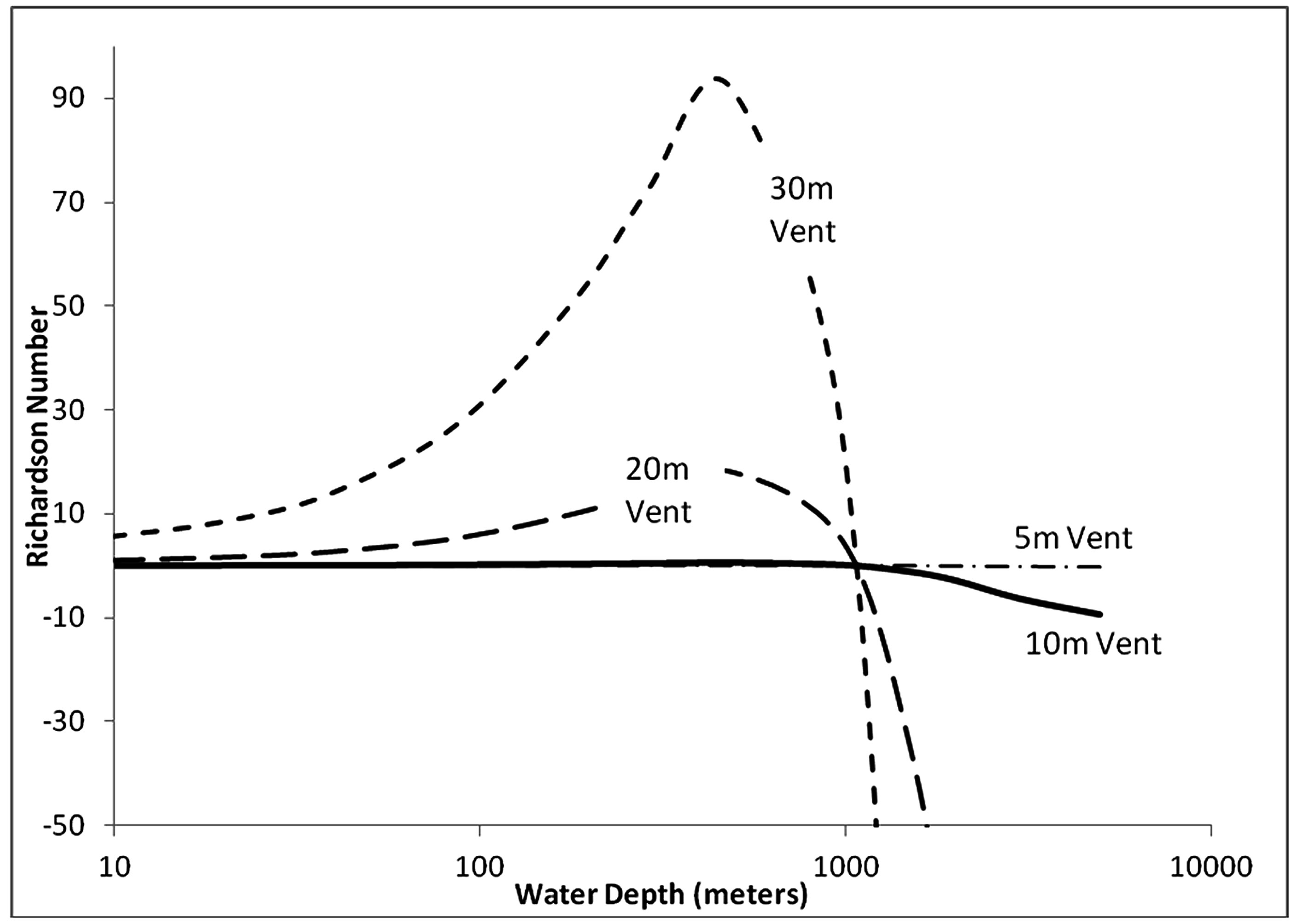
Figure 8. Effect of vent diameter on Richardson number. The effect of decreasing vent diameter is similar to increasing the flow rate (see Figure 7).
Figure 9 maps the effect of water content, depth and flow rate on the expected flow conditions for 1200˚C magma. The curve labeled “Positive Buoyancy Threshold” shows the water content as a function of depth that is necessary for the eruption to be positively buoyant. Eruptions falling along this curve will have a Richardson number equal to zero, regardless of flow conditions (vent size and eruption rate). The water content associated with 75% vesicularity (the nominal fragmentation threshold) is also shown as a function of water depth. Under film