The p.q.-Baer Property of Fixed Rings under Finite Group Action ()
1. Introduction
Throughout this paper all rings are associative with identity. Recall from [1] that a ring R is called right principally quasi-Baer (simply, right p.q.-Baer) if the right annihilator of every principal right ideal of R is generated, as a right ideal, by an idempotent of R. A left principally quasi-Baer (simply, left p.q.-Baer) ring is defined similarly. Right p.q.-Baer rings have been initially studied in [1]. For more details on (right) p.q.-Baer rings, see [1-6].
Recall from [7] (see also [8]) that a ring R is called quasi-Baer if the right annihilator of every right ideal is generated, as a right ideal, by an idempotent of R. A ring R is called biregular if for each
, 
for some central idempotent
. We note that the class of right p.q.-Baer rings is a generalization of the classes of quasi-Baer rings and biregular rings.
For a ring R, we use 
to denote a fixed maximal right ring of quotients of R. According to [9] an idempotent
of a ring
is called left (resp., right) semicentral if 
(resp.,
) for all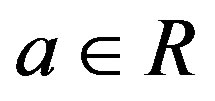
. Equivalently, an idempotent
is left (resp., right) semicentral if and only if eR (resp.,
) is a two-sided ideal of R. For a ring R, we let 
(resp.,
) denote the set of all left (resp., right) semicentral idempotents. An idempotent
of a ring
is called semicentral reduced if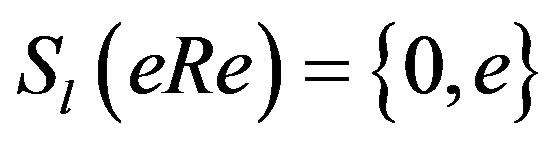
. Recall from [2] that a ring R is called semicentral reduced if
, i.e., 1 is a semicentral reduced idempotent of R.
For a nonempty subset X of a ring R, we use 
and 
to denote the right annihilator and the left annihilator of X in R, respectively. If R is a semiprime ring and I is a two-sided ideal of R, then
. For a right R-module
and a submodule N of M, we use 
and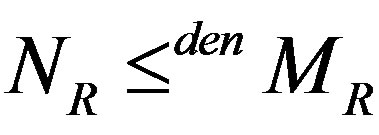 
to denote that 
is essential in 
and 
is dense in
, respectively.
For a ring R, we let 
denote the group of ring automorphisms of R. Let 
be a subgroup of
. For 
and
, we let 
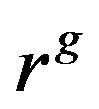denote the image of r under g. We use 
to denote the fixed ring of R under G, that is
.
We begin with the following example.
2. Preliminary
Example 2.1. There exist a ring R and a finite group G of ring automorphisms of R such that R is right p.q.-Baer but RG is not right p.q.-Baer. Let 
with a field F of characteristic 2. Then R is right p.q.-Baer. Define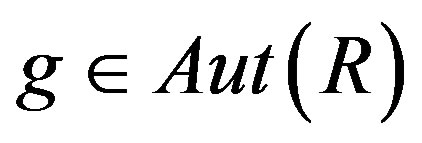 
by
Then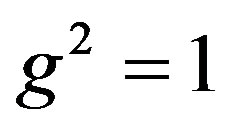 
since the characteristic of F is 2.
Now we show that RG is not right p.q.-Baer. The fixed ring under G is
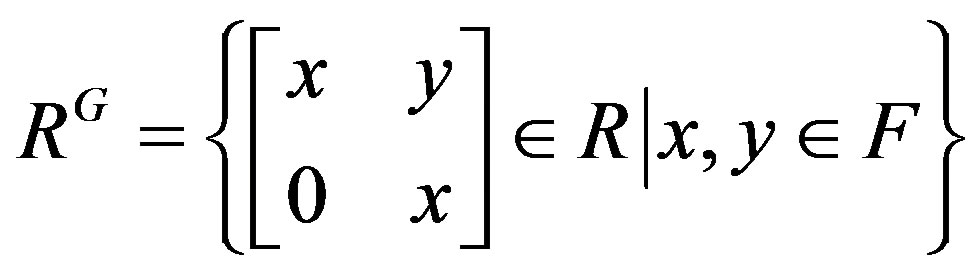
By computation we see that the idempotents of RG are only 0 and 1, thus RG is semicentral reduced. So if RG is right p.q.-Baer, then RG is a prime ring by [2, Lemma 4.2], a contradiction. Thus RG is not right p.q.-Baer.Also we can see that RG is not left p.q.-Baer.
Definition 2.2. Let R be a semiprime ring. For 
, let
where 
is the Martindale right ring of quotients of R (see [10] for more on
). We say that
is Xouter if
. A subgroup G of 
is called Xouter on R if every 
is X-outer. Assume that R is a semiprime ring, then for
, let
.
For
, we claim that
. Obviously
. Conversely, if 
then
. There exists 
such that
. Therefore
, 
, and
. Thus
, hence
. Therefore
. So if G is X-outer on R, then G can be considered as a group of ring automorph-ismms of 
and G is X-outer on
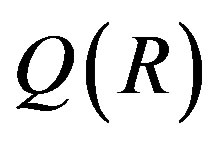. For more details for X-outer ring automorphisms of a ring, etc., see [10, p. 396] and [11].
We say that a ring R has no nonzero n-torsion (n is a positive integer) if 
with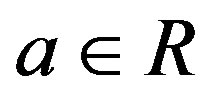 
implies
.
Lemma 2.3. [12,13]
Let R be a semiprime ring and G a group of ring automorphisms of R. If 
is semiprime, then 
is semiprime.
For a ring R, we use 
to denote the center of R.
Lemma 2.4. For a semiprime ring R, let G be a group of X-outer ring automorphisms of R.
Then
.
Proof.
Let 
with
, 1 the identity of G, and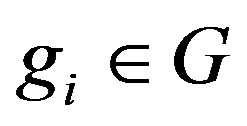
.
The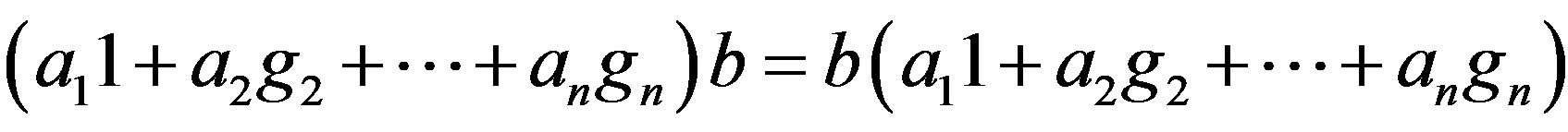 
for all
. So
, 
, ···, 
for all
. Since G is X-outer, it follows that
. Hence
. Also since 
for all
, we have that
.
Note that for all
, 
implies
. So
. Thus
.
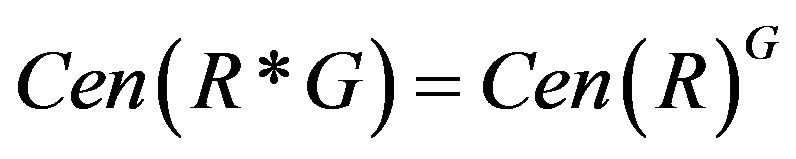Conversely, 
is clear.
Therefore
.
Lemma 2.5. [14] Assume that R is a semiprime ring and G is a finite group of X-outer ring automorphisms of R. Then
.
Lemma 2.6. Assume that R is a semiprime ring and
. Let
be a two-sided ideal of R such that 
and 
with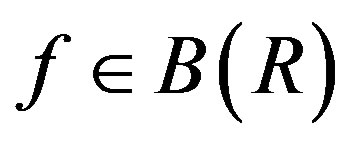
. Then
.
Proof. Since R is semiprime,
. Thus
. As
,
. We note that e and 
are in
. So we have that
.
Lemma 2.7. [15] Let R be a semiprime ring with a finite group G of X-outer ring automorphisms of R.
1) For
, let I be a dense right ideal I of RG such that
. Then IR is a dense right ideal of R and the map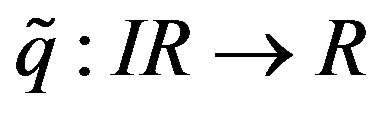 
defined by
, with 
and
, is a right R-homomorphism. Moreover
.
2) The map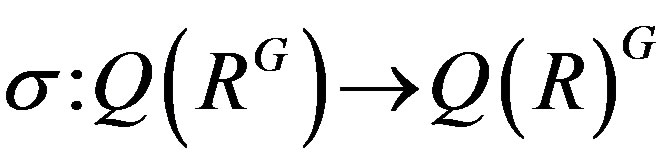 
defined by 
is a ring isomorphism.
3) Let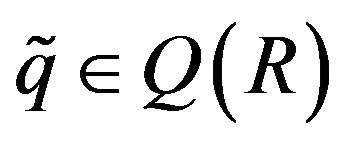 
and K a dense right ideal of R such that
. Then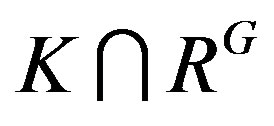 
is a dense right ideal of RG
and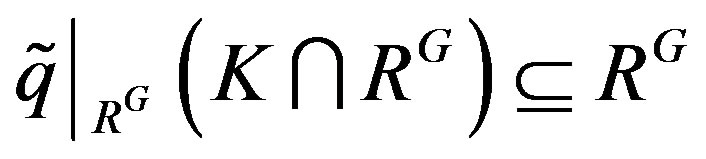
, where 
is the restriction of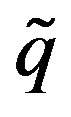 
to RG. Thus
.
For a ring R with a group G of ring automorphism of R, we say that a right ideal I of R is G-invariant if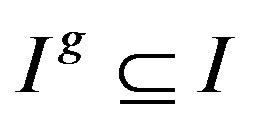 
for every
, where
.
Proposition 2.8. [1] Let R be a semiprime ring. Then the followings are equivalent.
1) R is right p.q.-Baer;
2) Every principal two-sided ideal of R is right essential in a ring direct summand of R;
3) Every finitely generated two-sided ideal of R is right essential in a ring direct summand of R;
4) Every principal two-sided ideal of R that is closed as a right ideal is a direct summand of R;
5) For every principal two-sided ideal I of R, 
is right essential in a direct summand of R;
6) R is left p.q.-Baer.
For a ring R with a group G of ring automorphisms of R, we say that a right ideal I of R is G-invariant if 
for every
, where
. Assume that R is a semiprime ring with a group G of ring automorphisms of R. We say that R is G-p.q.-Baer if the right annihilator of every finitely generated G-invariant two-sided ideal is generated by an idempotent, as a right ideal. By Proposition 8, if a ring R is semiprime p.q.- Baer with a group G of ring automorphisms of R, then R is G-p.q.-Baer.
A ring R is called right Rickart if the right annihilator of each element is generated by an idempotent of R. A left Rickart ring is defined similarly. A ring R is called Rickart if R is both right and left Rickart. A ring R is said to be reduced if R has no nonzero nilpotent element. We note that reduced Rickart rings are p.q.-Baer rings.
We put
Let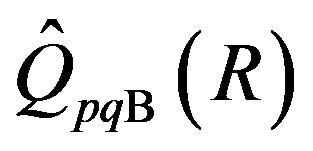 
be the subring of 
generated by R and
.
Lemma 2.9. [16] Assume that R is a semiprime ring. Then:
1) The ring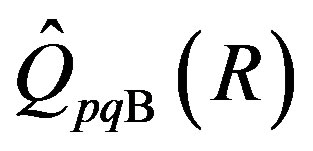 
is the smallest right ring of quotients of
which is p.q.-Baer;
2) R is p.q.-Baer if and only if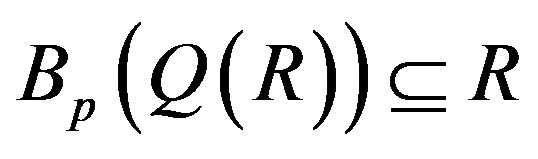
.
With these preparations, in spite of Example 1, we have the following result for p.q.-Baer property of RG on a semiprime ring R for the case when G is finite and X-outer.
3. Main Results
Theorem 3.1. Let R be a semiprime ring with a finite group G of X-outer ring automorphisms of R. Then:
1) If R is G-p.q.-Baer, then RG is p.q.-Baer.
2) If R is reduced G-p.q.-Baer, then RG is Rickart.
Proof. 1) Assume that R is G-p.q.-Baer. To show that RG is p.q.-Baer, it is enough to see that 
by Lemma 9 since RG is semiprime from Lemma 3. Let
. Then
, so 
by Lemma 7. From Lemma 9, there exists 
such that 
because
. Note that
.
We show that
. To see this, say
with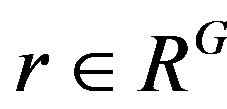
. Then
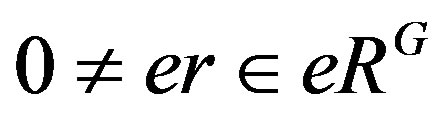. So there exists 
such that
. Hence 
.
Observe that
, as RG is semiprime from Lemma 3. So 
is a dense right ideal of RG since RG is semiprime. By Lemma 7, 
is a dense right ideal of
. So it is essential in
. Hence
.
We claim that
.
First note that
. For the claim, it is enough to show that
. Take
with
. Then there exists
such that
. Say
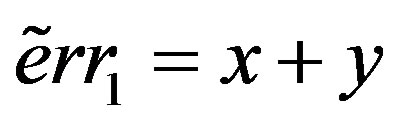, where 
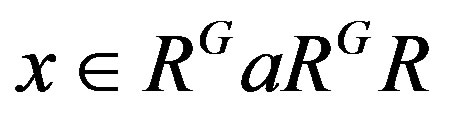and 
.
Then
.
Put 
with 
and
. Then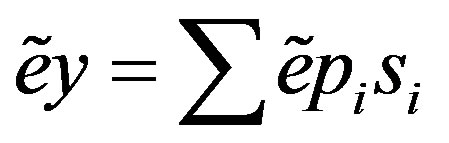
. In this case, 
for all i. To see this, assume on the contrary that there is 
such that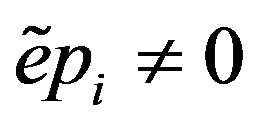
. Note that
.
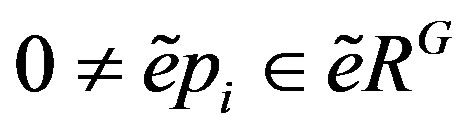Thus there exists 
such that 
because
.
Also 
because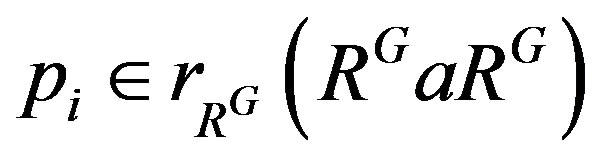 
. Therefore we have that 
, a contradiction. Thus 
for all i, so
. Hence
. Now since
, write 
with 
and
. Then 
because
. So
. Therefore
. Note that
by Lemma 5. Therefore
Hence
.
As RaR is a G-invariant two-sided ideal of R and R is R-p.q.-Baer, there is 
such that 
. From [9],
. As 
and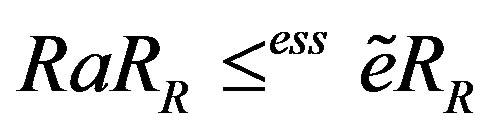
, it follows that 
by Lemma 6, so
.
Therefore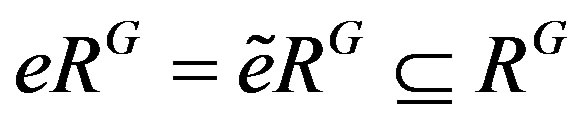
, and thus
.
So
, and hence RG is p.q.-Baer by Lemma 9.
2) We recall that a reduced p.q.-Baer ring is Rickart. Thus if R is reduced G-p.q.-Baer, then RG is Rickart from 1).
4. Conclusion
In [14], the quasi-Baer property of fixed rings under finite group actions on a semiprime ring and their applications to C*-algebras have been studied (see also [17,18]). Motivated by investigations in [14], in this paper we investigate the right p.q.-Baer property of fixed rings under finite group actions on a given semiprime ring. Assume that R is a semiprime ring with a finite group G of X-outer ring automorphisms of R. Then we show that if R is G-p.q.-Baer, then RG is p.q.-Baer. Thus if R is a semiprime p.q.-Baer ring with finite group G of X-outer ring automorphisms of R, then RG is p.q.-Baer.
NOTES