A Cubic Spline Method for Solving a Unilateral Obstacle Problem ()
1. Introduction
Let  be a bounded open domain in
be a bounded open domain in 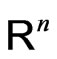 with smooth boundary
with smooth boundary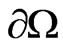 , and let
, and let 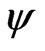 be an element of
be an element of 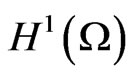 with
with  on
on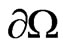 . Set
. Set

We consider the following variational inequality problem:
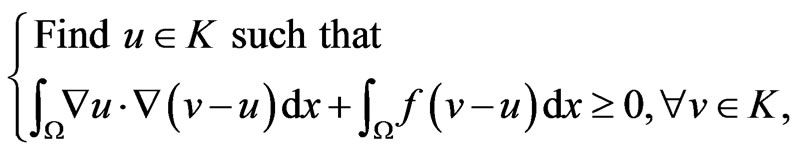 (1)
(1)
where f is an element of . This problem is called a unilateral obstacle problem. It is well known that problem (1) admits a unique solution u, and if
. This problem is called a unilateral obstacle problem. It is well known that problem (1) admits a unique solution u, and if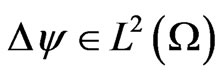 , then u is an element of
, then u is an element of 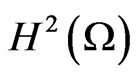 (see [1,2]). There are several alternative solution methods of the obstacle problem; see, e.g., [1,3-5]. Numerical solution by penalty methods have been considered, e.g. by [4,6]. In this paper we develop a numerical method for solving a one dimentional obstacle problem by using the cubic spline collocation method and the generalized Newton method. First, problem (1) is approximated by a sequence of nonlinear equation problems by using the penalty method given in [2,7]. Then we apply the spline collocation method to approximate the solution of a boundary value problem of second order. The discret problem is formulated as to find the cubic spline coefficients of a nonsmooth system
(see [1,2]). There are several alternative solution methods of the obstacle problem; see, e.g., [1,3-5]. Numerical solution by penalty methods have been considered, e.g. by [4,6]. In this paper we develop a numerical method for solving a one dimentional obstacle problem by using the cubic spline collocation method and the generalized Newton method. First, problem (1) is approximated by a sequence of nonlinear equation problems by using the penalty method given in [2,7]. Then we apply the spline collocation method to approximate the solution of a boundary value problem of second order. The discret problem is formulated as to find the cubic spline coefficients of a nonsmooth system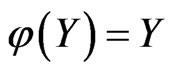 , where
, where . In order to solve the nonsmooth equation we apply the generalized Newton method (see [8-10], for instance). We prove that the cubic spline collocation method converges quadratically provided that a property coupling the penalty parameter
. In order to solve the nonsmooth equation we apply the generalized Newton method (see [8-10], for instance). We prove that the cubic spline collocation method converges quadratically provided that a property coupling the penalty parameter  and the discretization parameter h is satisfied.
and the discretization parameter h is satisfied.
Numerical methods to approximate the solution of boundary value problems have been considered by several authors. We only mention the papers [11,12] and references therein, which use the spline collocation method for solving the boundary value problems.
The present paper is organized as follows. In Section 2, we present the penalty method to approximate the obstacle problem by a sequence of second order boundary value problems. In Section 3 we construct a cubic spline to approximate the solution of the boundary problem. Section 4 is devoted to the presentation of the generalized Newton method. In Section 5 we show the convergence of the cubic spline to the solution of the boundary problem and provide an error estimate. Finally, some numerical results are given in Section 6 to validate our methodology.
2. Penalty Problem
Let 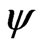 be an element of
be an element of  with
with 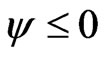 on
on . Assume that
. Assume that  is an element of
is an element of , then the solution u of problem (1) is an element of
, then the solution u of problem (1) is an element of 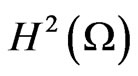 and can be characterized as (see [1], for instance):
and can be characterized as (see [1], for instance):
 (2)
(2)
The penalty problem is given by the following boundary value problem (see [10], p. 107, [12]):
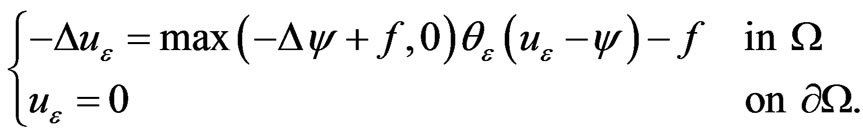 (3)
(3)
where 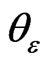 is a sequence of Lipschitz functions which tend to the function
is a sequence of Lipschitz functions which tend to the function 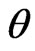 defined by
defined by
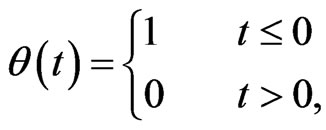 (4)
(4)
almost everywhere on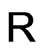 , as
, as 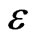 goes to zero. Assume that the function
goes to zero. Assume that the function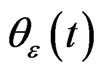 ,
, 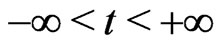 , is uniformly Lipschitz, non increasing and satisfy
, is uniformly Lipschitz, non increasing and satisfy . Then problem (3) admits a unique solution (see [2] p. 107). We now specify the function
. Then problem (3) admits a unique solution (see [2] p. 107). We now specify the function
 (5)
(5)
We have the interesting properties.
Theorem 1 ([2,7]) Let u denote the solution of the variational inequality problem (1) and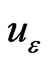 ,
, 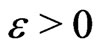 , denotes the solution of the penalty problem (3) with
, denotes the solution of the penalty problem (3) with 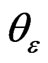 defined by relation (5). Then
defined by relation (5). Then 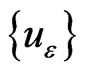 is a nondecreasing sequence and
is a nondecreasing sequence and

3. Cubic Spline Collocation Method
In this section we construct a cubic spline which approximates the solution 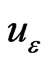 of problem (3), with
of problem (3), with  is the interval
is the interval  and
and  is the function given by (5).
is the function given by (5).
Cubic Spline Solution
Let
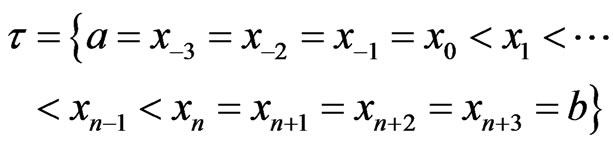
be a subdivision of the interval I. Without loss of generality, we put , where
, where 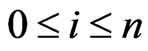 and
and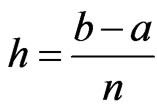 .
.
Denote by 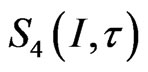 the space of piecewise polynomials of degree 3 over the subdivision
the space of piecewise polynomials of degree 3 over the subdivision  and of class
and of class 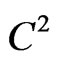 everywhere on
everywhere on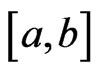 . Let
. Let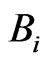 ,
, 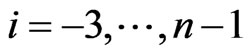 , be the B-splines of degree 3 associated with
, be the B-splines of degree 3 associated with . These Bsplines are positives and form a basis of the space
. These Bsplines are positives and form a basis of the space . If we put
. If we put
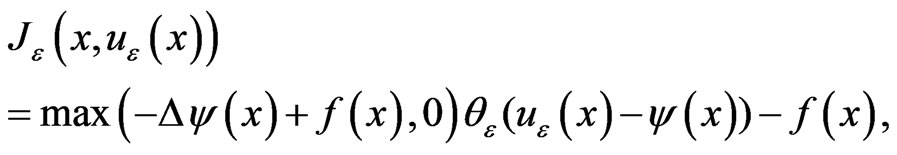 (6)
(6)
then problem (3) becomes
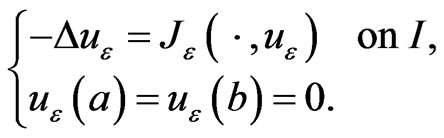 (7)
(7)
It is easy to see that  is a nonlinear continuous function on
is a nonlinear continuous function on ; and for any two functions
; and for any two functions 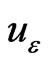 and
and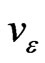 ,
,  satisfies the following Lipschitz condition:
satisfies the following Lipschitz condition:
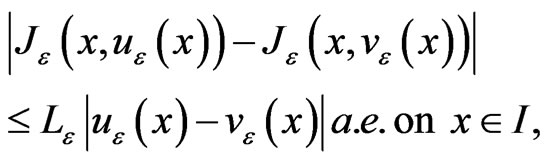 (8)
(8)
where

Now, we define the following interpolation cubic spline of the solution 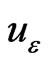 of the nonlinear second order boundary value problem (7).
of the nonlinear second order boundary value problem (7).
Proposition 2 Let  be the solution of problem (7). Then, there exists a unique cubic spline interpolant
be the solution of problem (7). Then, there exists a unique cubic spline interpolant 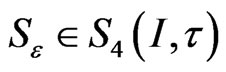 of
of  which satisfies:
which satisfies:
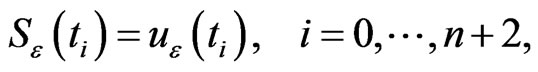
where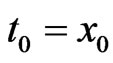 ,
, 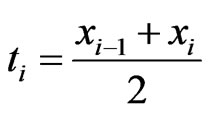 ,
, 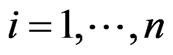 ,
,  and
and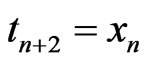 .
.
Proof Using the Schoenberg-Whitney theorem (see [13]), it is easy to see that there exits a unique cubic spline which interpolates  at the points
at the points ,
,  .
.
If we put , then by using the boundary conditions of problem (7) we obtain
, then by using the boundary conditions of problem (7) we obtain
 , and
, and
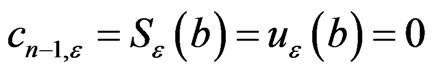
Hence 
Furthermore, since the interpolation with splines of degree d gives uniform norm errors of order 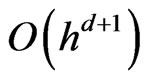 for the interpolant, and of order
for the interpolant, and of order 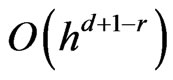 for the
for the  derivative of the interpolant (see [13], for instance), then for any
derivative of the interpolant (see [13], for instance), then for any 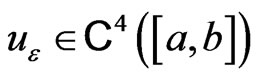 we have
we have
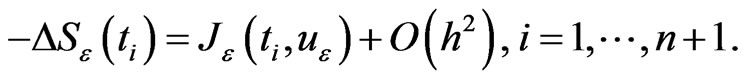 (9)
(9)
The cubic spline collocation method, that we present in this paper, constructs numerically a cubic spline 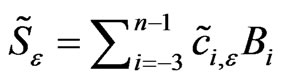 which satisfies the Equation (7) at the points
which satisfies the Equation (7) at the points ,
, . It is easy to see that
. It is easy to see that
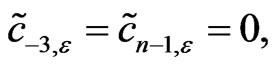
and the coefficients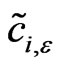 ,
, 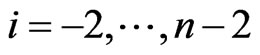 , satisfy the following nonlinear system with n + 1 equations:
, satisfy the following nonlinear system with n + 1 equations:
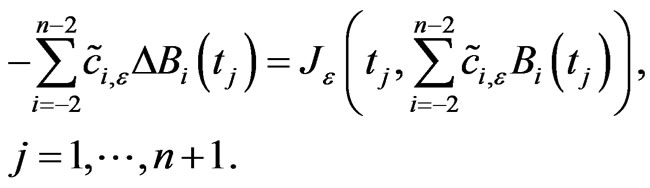 (10)
(10)
Relations (9) and (10) can be written in the matrix form, respectively, as follows
 (11)
(11)
where
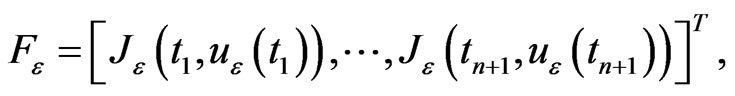

and  is a vector where each component is of order
is a vector where each component is of order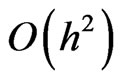 . It is well known that
. It is well known that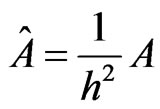 , where A is a matrix independent of h given as follows:
, where A is a matrix independent of h given as follows:

Then, relation (11) becomes
 (12)
(12)
with  is a vector where each one of its components is of order
is a vector where each one of its components is of order .
.
The results of this work are basically based on the invertibility of the matrix A. Then, in order to prove that A is invertible we give the flowing lemma.
Lemma 3 (de Boor [13]) Let  such that
such that 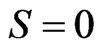 on
on  where
where . If S admits r zeros in
. If S admits r zeros in  then
then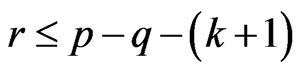 .
.
Proposition 4 The matrix A is invertible.
Proof Let 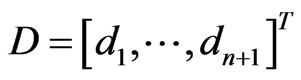 be a vector of
be a vector of 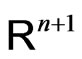
such that . If we put
. If we put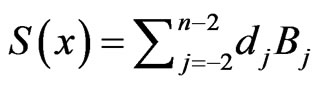 , then we have
, then we have 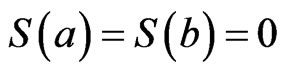 and
and 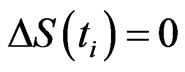 for any
for any . Since
. Since 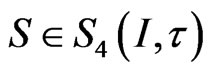 then
then . If we assume that
. If we assume that 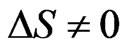 in
in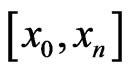 , then using the above lemma and the fact that
, then using the above lemma and the fact that 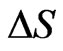 has
has  zeros in
zeros in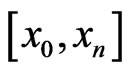 , we conclude that
, we conclude that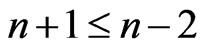 , which is impossible. Therefore
, which is impossible. Therefore  for each
for each . This means that the function S is a piecewise linear polynomial in I. Since
. This means that the function S is a piecewise linear polynomial in I. Since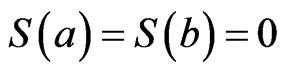 , then we obtain
, then we obtain  for any
for any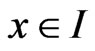 . Consequently
. Consequently 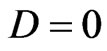 and the matrix A is invertible.
and the matrix A is invertible.
Proposition 5 Assume that the penalty parameter 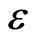 and the discretization parameter h satisfy the following relation:
and the discretization parameter h satisfy the following relation:
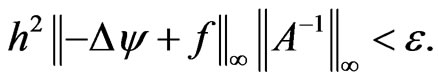 (13)
(13)
Then there exists a unique cubic spline which approximates the exact solution 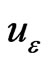 of problem (7).
of problem (7).
Proof From relation (12), we have . Let
. Let 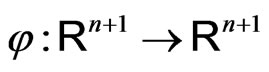 be a function defined by
be a function defined by
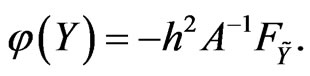 (14)
(14)
To prove the existence of cubic spline collocation it suffices to prove that 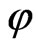 admits a unique fixed point. Indeed, let
admits a unique fixed point. Indeed, let 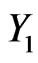 and
and 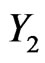 be two vectors of
be two vectors of . Then we have
. Then we have
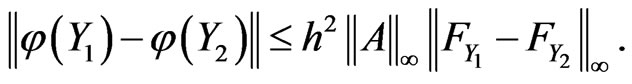 (15)
(15)
Using relation (8) and the fact that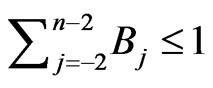 , we get
, we get
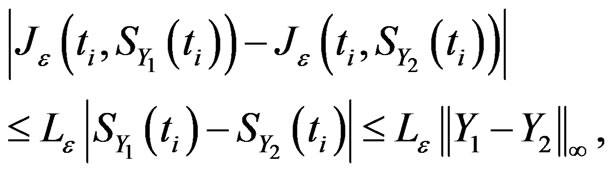
where . Then we obtain
. Then we obtain
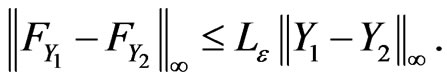
From relation (15), we conclude that
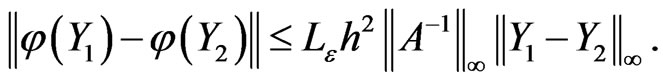
Then we have
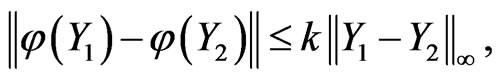
With 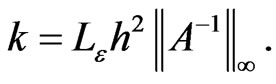
by relation (13). Hence the function  admits a unique fixed point.
admits a unique fixed point.
In order to calculate the coefficients of the cubic spline collocation given by the nonsmooth system
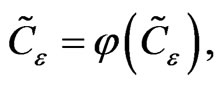 (16)
(16)
we propose the generalized Newton method defined by
 (17)
(17)
where 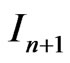 is the unit matrix of order
is the unit matrix of order 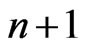 and
and  is the generalized Jacobian of the function
is the generalized Jacobian of the function , (see [8-10], for instance).
, (see [8-10], for instance).
4. Generalized Newton Method
Let 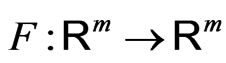 be a function. Consider the equation
be a function. Consider the equation

The Newton method assumes that F is Fréchet differentiable, and is defined by
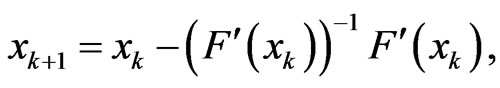 (18)
(18)
where 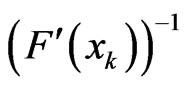 is the inverse of the Jacobian of the function F. However, in nonsmooth case
is the inverse of the Jacobian of the function F. However, in nonsmooth case  may not exists. The generalized Jacobian of the function F may play the role of
may not exists. The generalized Jacobian of the function F may play the role of  in the relation (18). Rademacher's theorem states that a locally Lipschitz function is almost everywhere differentiable (see [14], for instance). Assume that F is a locally Lipschitz function and let
in the relation (18). Rademacher's theorem states that a locally Lipschitz function is almost everywhere differentiable (see [14], for instance). Assume that F is a locally Lipschitz function and let 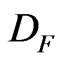 be the set where F is differentiable. We denote
be the set where F is differentiable. We denote
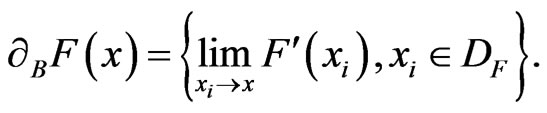
The generalized Jacobian of F at ,
, 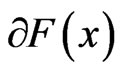 , in the sense of Clarke [15] is the convex hull of
, in the sense of Clarke [15] is the convex hull of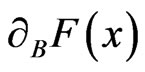 :
:
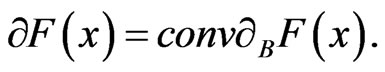 (19)
(19)
For nonsmooth equations with a locally Lipschitz function F, the generalized Newton method is defined by
 (20)
(20)
where 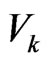 is an element of
is an element of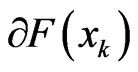 . If the function F is semismooth and BD-regular at x, then the sequence
. If the function F is semismooth and BD-regular at x, then the sequence 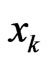 in (20) superlinearly converges to a solution x (see [8,9, 16,17]). A Function F is said to be BD-regular at a point x if all the elements of
in (20) superlinearly converges to a solution x (see [8,9, 16,17]). A Function F is said to be BD-regular at a point x if all the elements of 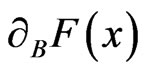 are nonsingular, and it is said to be semismooth at x if it is locally Lipshitz at x and the limit
are nonsingular, and it is said to be semismooth at x if it is locally Lipshitz at x and the limit

exists for any . The class of semismooth functions includes, obviously smooth functions, convex functions, the piecewise-smooth functions, and others (see [10,18], for instance). Since the function
. The class of semismooth functions includes, obviously smooth functions, convex functions, the piecewise-smooth functions, and others (see [10,18], for instance). Since the function 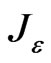 defined by (6) is a Lipshitz and piecewise smooth function on
defined by (6) is a Lipshitz and piecewise smooth function on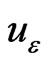 , then the function
, then the function 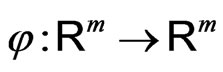 given by (14) is also a Lipshitz and piecewise smooth function on
given by (14) is also a Lipshitz and piecewise smooth function on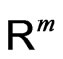 . Hence we may apply the generalized Newton method to solve the problem (16).
. Hence we may apply the generalized Newton method to solve the problem (16).
5. Convergence of the Method
Theorem 6 If we assume that the penalty parameter 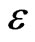 and the discretization parameter h satisfy the following relation
and the discretization parameter h satisfy the following relation
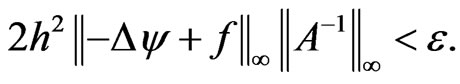 (21)
(21)
then the cubic spline  converges to the solution
converges to the solution .
.
Moreover the error estimate  is of order
is of order .
.
Proof From (12) and Lemma 4, we have
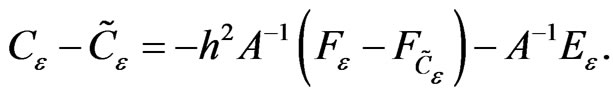
Since 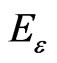 is of order
is of order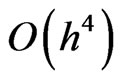 , then there exists a constant
, then there exists a constant 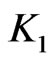 such that
such that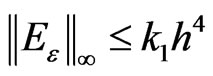 . Hence we have
. Hence we have
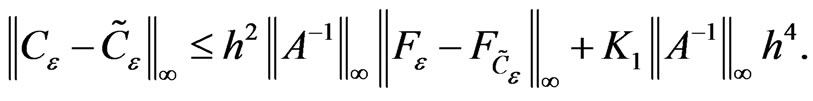 (22)
(22)
On the other hand we have
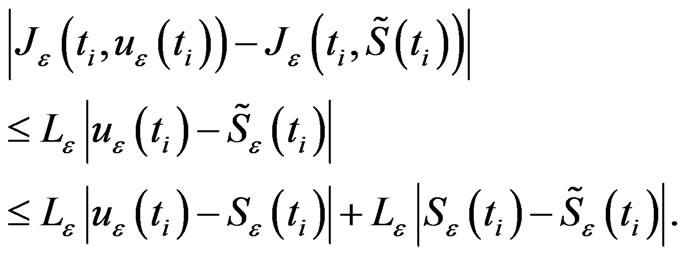
Since  is the cubic spline interpolation of
is the cubic spline interpolation of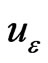 , then there exists a constant
, then there exists a constant 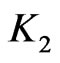 such that
such that
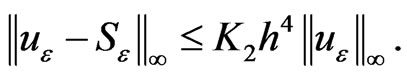 (23)
(23)
Using the fact that
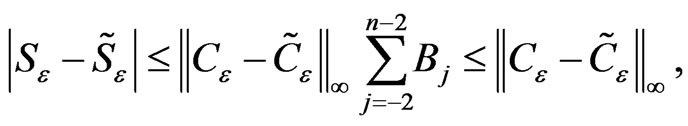 (24)
(24)
then, we obtain
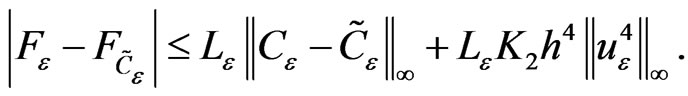
By using relation (22) and assumption (21) it is easy to see that
 (25)
(25)
We have
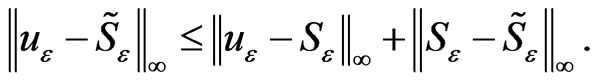
Then from relations (23), (24) and (25), we deduce that  is of order
is of order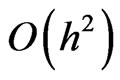 . Hence the proof is complete.
. Hence the proof is complete.
Remark 7 Theorem 6 provides a relation coupling the penalty parameter 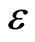 and the discretization parameter h, which guarantees the quadratic convergence of the cubic spline collocation
and the discretization parameter h, which guarantees the quadratic convergence of the cubic spline collocation 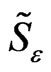 to the solution
to the solution  of the penalty problem.
of the penalty problem.
6. Numerical Examples
In this section we give numerical experiments in order to validate the theoretical results presented in this paper. We report numerical results for solving a one dimensional obstacle problem by using the cubic spline method to approximate the solution of the penalty problem (7), and the generalized Newton method (20) to determine the coefficients of the cubic spline collocation. Consider the obstacle problem (1) with the following data: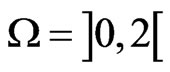 ,
, 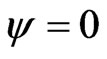 and
and

The true solution 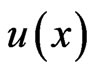 of this problem is given by
of this problem is given by

As a stopping criteria for the generalized Newton’s iterations, we have considered that the absolute value of the difference between the input coefficients and the output coefficients is less than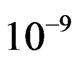 .
.
Tables 1-4 show, for different values of the discretization parameter h, the error between the cubic spline collocation 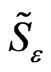 and the true solution u. We note the convergence of the solution
and the true solution u. We note the convergence of the solution 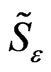 to the function u depends on the discretization parameter h and the penalty parameter
to the function u depends on the discretization parameter h and the penalty parameter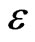 . Theorem 6 implies that for a fixed h, this convergence is guaranteed only if there exists
. Theorem 6 implies that for a fixed h, this convergence is guaranteed only if there exists  such that
such that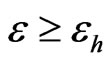 . Some experimental values of
. Some experimental values of 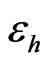 are given in Tables 1-4.
are given in Tables 1-4.
Theorems 1 and 6 imply that we have the error estimate between the exact solution and the discret penalty solution is given by . The obtained results show the convergence of the discret penalty solution to the solution of the original obstacle problem as
. The obtained results show the convergence of the discret penalty solution to the solution of the original obstacle problem as
the parameters h and 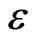 get smaller provided they satisfy the relation (21). Moreover, the numerical error estimates behave like
get smaller provided they satisfy the relation (21). Moreover, the numerical error estimates behave like 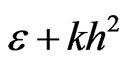 which confirms what we were expecting.
which confirms what we were expecting.
7. Concluding Remarks
In this paper, we have consider an approximation of a unilateral obstacle problem by a sequence of penalty problems, which are nonsmooth equation problems, presented in [2,7]. Then we have developed a numerical method for solving each nonsmooth equation, based on a cubic collocation spline method and the generalized Newton method. We have shown the convergence of the method provided that the penalty and discret parameters satisfy the relation (21). Moreover we have provided an error estimate of order  with respect to the norm
with respect to the norm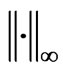 . The obtained numerical results show the convergence of the approximate penalty solutions to the exact one and confirm the error estimates provided in this paper.
. The obtained numerical results show the convergence of the approximate penalty solutions to the exact one and confirm the error estimates provided in this paper.
NOTES