A Unified Theory (I) for Neighborhood Systems and Basic Concepts on Fuzzifying Topological Spaces ()
1. Introduction
In the last few years fuzzy topology, as an important research field in fuzzy set theory, has been developed into a quite mature discipline [1-6]. In contrast to classical topology, fuzzy topology is endowed with richer structure, to a certain extent, which is manifested with different ways to generalize certain classical concepts. So far, according to Ref. [2], the kind of topologies defined by Chang [7] and Goguen [8] is called the topologies of fuzzy subsets, and further is naturally called L-topological spaces if a lattice L of membership values has been chosen. Loosely speaking, a topology of fuzzy subsets (resp. an L-topological space) is a family 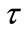 of fuzzy subsets (resp. L-fuzzy subsets) of nonempty set X, and
of fuzzy subsets (resp. L-fuzzy subsets) of nonempty set X, and  satisfies the basic conditions of classical topologies [9]. On the other hand, Höhle in [10] proposed the terminology L-fuzzy topology to be an L-valued mapping on the traditional powerset
satisfies the basic conditions of classical topologies [9]. On the other hand, Höhle in [10] proposed the terminology L-fuzzy topology to be an L-valued mapping on the traditional powerset  of X. The authors in [4,5,11,12] defined an L-fuzzy topology to be an L-valued mapping on the L-powerset LX of X. In 1952, Rosser and Turquette [13] proposed emphatically the following problem: If there are many-valued theories beyond the level of predicates calculus, then what are the detail of such theories? As an attempt to give a partial answer to this problem in the case of point set topology, Ying in 1991 [14,15] used a semantical method of continuousvalued logic to develop systematically fuzzifying topology. Briefly speaking, a fuzzifying topology on a set X assigns each crisp subset of X to a certain degree of being open, other than being definitely open or not. In factfuzzifying topologies are a special case of the L-fuzzy topologies in [11,12] since all the t-norms on I are included as a special class of tensor products in these paper. Ying uses one particular tensor product, namely Łukasiewicz conjunction. Thus his fuzzifying topologies are a special class of all the I-fuzzy topologies considered in the categorical frameworks [11,12]. Roughly speaking, the semantical analysis approach transforms formal statements of interest, which are usually expressed as implication formulas in logical language, into some inequalities in the truth value set by truth valuation rules, and then these inequalities are demonstrated in an algebraic way and the semantic validity of conclusions is thus established. So far, there has been significant research on fuzzifying topologies [16-21]. In 1979, several characterizations of compactness are unified by the operation introduced by Kasahara [22]. Also, he studied the concept of
of X. The authors in [4,5,11,12] defined an L-fuzzy topology to be an L-valued mapping on the L-powerset LX of X. In 1952, Rosser and Turquette [13] proposed emphatically the following problem: If there are many-valued theories beyond the level of predicates calculus, then what are the detail of such theories? As an attempt to give a partial answer to this problem in the case of point set topology, Ying in 1991 [14,15] used a semantical method of continuousvalued logic to develop systematically fuzzifying topology. Briefly speaking, a fuzzifying topology on a set X assigns each crisp subset of X to a certain degree of being open, other than being definitely open or not. In factfuzzifying topologies are a special case of the L-fuzzy topologies in [11,12] since all the t-norms on I are included as a special class of tensor products in these paper. Ying uses one particular tensor product, namely Łukasiewicz conjunction. Thus his fuzzifying topologies are a special class of all the I-fuzzy topologies considered in the categorical frameworks [11,12]. Roughly speaking, the semantical analysis approach transforms formal statements of interest, which are usually expressed as implication formulas in logical language, into some inequalities in the truth value set by truth valuation rules, and then these inequalities are demonstrated in an algebraic way and the semantic validity of conclusions is thus established. So far, there has been significant research on fuzzifying topologies [16-21]. In 1979, several characterizations of compactness are unified by the operation introduced by Kasahara [22]. Also, he studied the concept of  -continuity (where
-continuity (where  is an operation) and defined some types of spaces by using this operation. In 1981, the concept of other type of continuity which generalizes the
is an operation) and defined some types of spaces by using this operation. In 1981, the concept of other type of continuity which generalizes the  -continuity [22] was introduced by Jankoviĉ [23]. In 1983, Abd El-Monsef, et al. [24] introduced an operation
-continuity [22] was introduced by Jankoviĉ [23]. In 1983, Abd El-Monsef, et al. [24] introduced an operation  on the family
on the family  of all closed sets in the topological space
of all closed sets in the topological space  which is dual to the operation
which is dual to the operation  . In 1991, Kerre et al. [25] introduced an extension of the concept of an operation on the class of all fuzzy sets on X endowed with Chang fuzzy topology [7]. It was shown that a lot of characterizations and properties of many concepts and stronger forms can be unified by using this notion. In 1991, Kandil et al. [26] applied the concept of the operation defined in [25] to unify and generalize several characterizations and properties of a lot of already existing weaker and stronger forms of fuzzy continuity. A basic structure of this paper is as follows: First, in Section 2 we offer some definition and results which will be needed in this paper. In Section 3 the concepts of fuzzifying ∆-open sets, C∆-open sets, ∆-closed sets and C∆-closed sets are introduced and some of their properties are discussed. In Section 4 the fuzzifying ∆- and C∆-neighborhood systems are presented and a fuzzifying topology induced by C∆- neighborhood system is introduced. In Section 5 the concepts of fuzzifying ∆- and C∆-derived sets, ∆- and C∆-closure operations and ∆- and C∆-interior operations were established and some of their properties are studied. Finally, in Section 6, we summarize the main results obtained and raise some related problems for further study. Thus we fill a gap in the existing literature on fuzzifying topology.
. In 1991, Kerre et al. [25] introduced an extension of the concept of an operation on the class of all fuzzy sets on X endowed with Chang fuzzy topology [7]. It was shown that a lot of characterizations and properties of many concepts and stronger forms can be unified by using this notion. In 1991, Kandil et al. [26] applied the concept of the operation defined in [25] to unify and generalize several characterizations and properties of a lot of already existing weaker and stronger forms of fuzzy continuity. A basic structure of this paper is as follows: First, in Section 2 we offer some definition and results which will be needed in this paper. In Section 3 the concepts of fuzzifying ∆-open sets, C∆-open sets, ∆-closed sets and C∆-closed sets are introduced and some of their properties are discussed. In Section 4 the fuzzifying ∆- and C∆-neighborhood systems are presented and a fuzzifying topology induced by C∆- neighborhood system is introduced. In Section 5 the concepts of fuzzifying ∆- and C∆-derived sets, ∆- and C∆-closure operations and ∆- and C∆-interior operations were established and some of their properties are studied. Finally, in Section 6, we summarize the main results obtained and raise some related problems for further study. Thus we fill a gap in the existing literature on fuzzifying topology.
Note: All corollaries in this paper are results in [14- 21].
2. Preliminaries
We present the fuzzy logical and corresponding set theoretical notations [14,15] since we need them in this paper.
For any formula , the symbol
, the symbol  means the truth value of
means the truth value of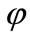 , where the set of truth values is the unit interval [0, 1]. We write
, where the set of truth values is the unit interval [0, 1]. We write  if
if  for any interpretation. Also,
for any interpretation. Also,  is the family of all fuzzy sets in X. The truth valuation rules for primary fuzzy logical formulae and corresponding set theoretical notations are:
is the family of all fuzzy sets in X. The truth valuation rules for primary fuzzy logical formulae and corresponding set theoretical notations are:
1) a) ;
;
b)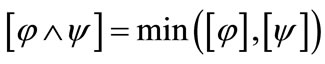 ;
;
c) .
.
2) If 
3) If X is the universe of discourse, then
 .
.
In addition the truth valuation rules for derived formulae are:
1) ;
;
2) ;
;
3) 
4) ;
;
5)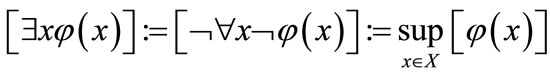 ;
;
6) If , then
, then
a) 

b) ;
;
c) .
.
We give now the following definitions and results in fuzzifying topology [14-21] which are used in the sequel.
Definition 2.1 [14]. Let X be a universe of discourse, and  satisfy the following conditions:
satisfy the following conditions:
1) ;
;
2) for any 
3) for any
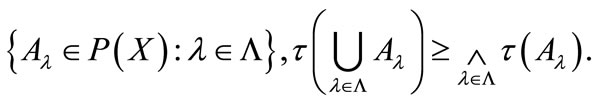
Then  is a fuzzifying topology and
is a fuzzifying topology and  is a fuzzifying topological space.
is a fuzzifying topological space.
Note: In the rest of this paper  (or briefly X) is always fuzzifying topological space.
(or briefly X) is always fuzzifying topological space.
Definition 2.2 [14] The family of all fuzzifying closed sets, denoted by 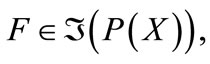 is defined as
is defined as  where
where  is the complement of A.
is the complement of A.
Definition 2.3 [14] The neighborhood system  of
of  is defined as
is defined as

Definition 2.4 [15] The interior  or
or  of
of  is defined as
is defined as 
Definition 2.5 (Lemma 5.2. [14]). The closure  or
or  of A is defined as
of A is defined as . In Theorem 5.3 [14], Ying proved that the closure
. In Theorem 5.3 [14], Ying proved that the closure
 sssis a fuzzifying closure operator since its extension
sssis a fuzzifying closure operator since its extension 
 ,
,  where
where  is the
is the  -cut of A and
-cut of A and  satisfies the following Kuratowski closure axioms:
satisfies the following Kuratowski closure axioms:
1) 
2) for any 

3) for any
4) for any 
Definition 2.6 [18] For any ,
,
 .
.
Theorem 2.1 [18] For any 
1) 
2) 
3) 
4) 
Theorem 2.2 [18] For any , if
, if  then
then
1) 
2) 
3) 
4) 
5) 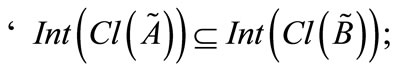
6) 
Theorem 2.3 For any
1)  [19];
[19];
2)  [18];
[18];
3)  [18];
[18];
4)  [16].
[16].
Theorem 2.4
1) 
2) 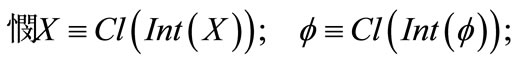
3) 
4) 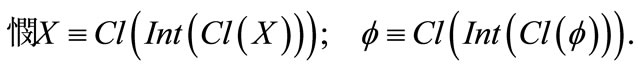
Theorem 2.5 For any
1) 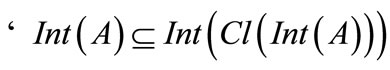 [19];
[19];
2) 
3) 
4) 
5) 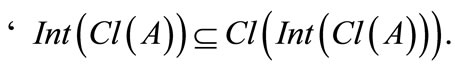
Theorem 2.6 For any
1) 
2) 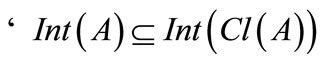 [17];
[17];
3) 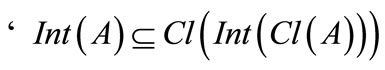 [16].
[16].
Definition 2.7 Let X be a non-empty set.
1) By the symbol 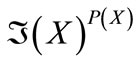 we denote the set of all functions from
we denote the set of all functions from 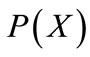 into
into . Each member of
. Each member of  will be called a general fuzzifying operation.
will be called a general fuzzifying operation.
2) Let .
.
a) We say that , if
, if 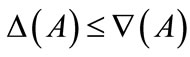 for each
for each 
b) We say that 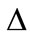 and
and  are dual if
are dual if
 equivalently
equivalently
 for each
for each 
3) A general fuzzifying operation  is said to be monotone if
is said to be monotone if 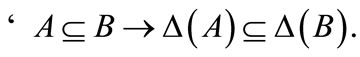
4) A general fuzzifying operation  is said to be of type
is said to be of type 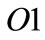 if
if ; equivalently
; equivalently , where
, where  and
and  are dual.
are dual.
5) A general fuzzifying operation  is said to be of type
is said to be of type  if
if  for any
for any 
Example 2.1
1) From Theorem 2.4 we have 
 ,
,  and
and  are of type
are of type  and each member of them is monotone from Theorem 2.2.
and each member of them is monotone from Theorem 2.2.
2) The fuzzifying operations ,
, 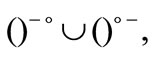 and
and  and the fuzzifying operations
and the fuzzifying operations ,
,
 and
and  are dual respectively (see Theorem 2.3).
are dual respectively (see Theorem 2.3).
3) From Theorem 2.1 (3),  is of type
is of type .
.
4) From Theorem 2.5, one can easily deduce that:
a) 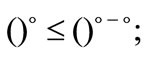
b) 
c) 
d) 
e) 
f) 
g) 
Note: In the rest of this paper always .
.
3. Fuzzifying Open Sets
In this section the concepts of fuzzifying ∆-open sets, C∆-open sets, ∆-closed sets and C∆-closed sets are introduced and some of their properties are discussed.
Definition 3.1 1) The family of all fuzzifying ∆-open sets, denoted by  is defined as follows:
is defined as follows:

i.e.,

2) The family of all fuzzifying C∆-open sets, denoted by  is defined as follows:
is defined as follows:

i.e.,
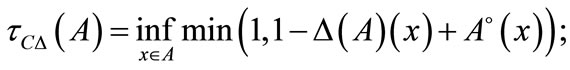
3) The family of all fuzzifying ∆ (resp. C∆-closed sets, denoted by  (resp.
(resp. )
)  is defined as follows:
is defined as follows:

Definition 3.2 1) If  (resp.
(resp. ,
,  , the notion of fuzzifying ∆-open sets coincides with the notion of fuzzifying open (resp.
, the notion of fuzzifying ∆-open sets coincides with the notion of fuzzifying open (resp.  - open, semi-open, pre-open,
- open, semi-open, pre-open,  -open,
-open,  -open) sets and will be denoted by
-open) sets and will be denoted by  (resp.
(resp. );
);
2) If  (resp.
(resp. , the notion of fuzzifying C∆-open sets coincides with the notion of fuzzifying
, the notion of fuzzifying C∆-open sets coincides with the notion of fuzzifying  (resp. csemi, cpre,
(resp. csemi, cpre,  ,
, )- open sets and will be denoted by
)- open sets and will be denoted by  (resp.
(resp. ,
, );
);
3) If  (resp.
(resp. , the notion of fuzzifying
, the notion of fuzzifying  -closed sets coincides with the notion of fuzzifying closed (resp.
-closed sets coincides with the notion of fuzzifying closed (resp.  -closed, semiclosed, pre-closed,
-closed, semiclosed, pre-closed,  -closed,
-closed,  -closed) sets and will be denoted by
-closed) sets and will be denoted by  (resp.
(resp. );
);
4) If  (resp.
(resp. , the notion of fuzzifying C∆-closed sets coincides with the notion of fuzzifying
, the notion of fuzzifying C∆-closed sets coincides with the notion of fuzzifying  (resp. csemi, cpre,
(resp. csemi, cpre,  ,
, )-closed sets and will be denoted by
)-closed sets and will be denoted by  (resp.
(resp. );
);
Theorem 3.1 1) If ∆ is of type O1, then
a) 

b) 

2) If ∆ is monotone, then a) for any 

b) for any 

Proof. 1) a) 

b) 

2) a) Since  is monotone, then
is monotone, then

b) For any 

(see Lemma 1.1 (1) [14]). Since ∆ is monotone, then from Theorem 2.1 (3) we have

Corollary 3.1 1) a) 

b) for any 
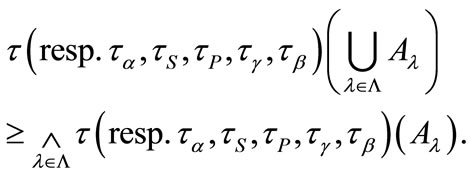
2) a) 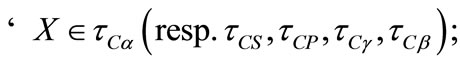
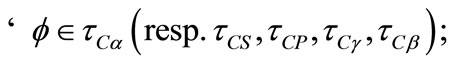
b) for any 

Theorem 3.2 1) If ∆ is of type O1, then
a) 

b) 

2) If ∆ is monotone, then a) for any 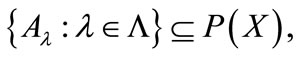

b) for any 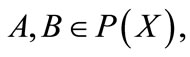

Proof. It is immediate from Theorem 3.1.
Corollary 3.2 1) a) 

b) 

2) a) for any 

b) for any 

Theorem 3.3 1) 
2) , where
, where  is the dual of
is the dual of 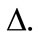
Proof.
1) 

2) 
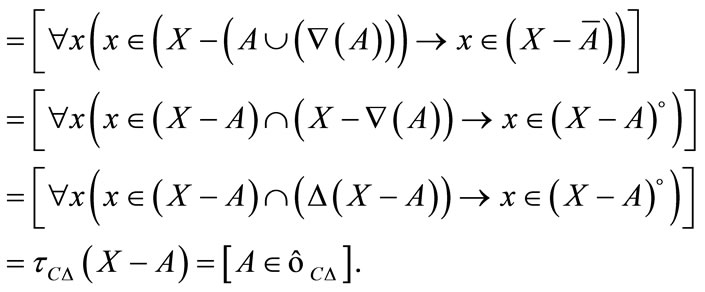
Corollary 3.3
1) 

2) 

Theorem 3.4 Let 
1) If , a)
, a)  b)
b)  c)
c)  d)
d) 
2) a)  b)
b) 
Proof.
1) a) 
b) From a) above, we have
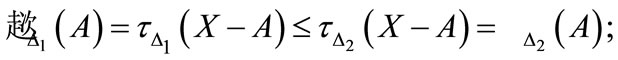
c) 

d) From (c) above, we have 
2) a) 
b) From a) above, we have

Corollary 3.4 1) a) i)  ii)
ii)  iii)
iii)  iv)
iv)  (v)
(v)  (vi)
(vi) 
b) i)  ii)
ii) 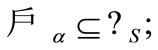 iii)
iii)  iv)
iv)  v)
v)  vi)
vi) 
c) i)  ii)
ii)  iii)
iii)  iv)
iv)  v)
v) 
d) i)  ii)
ii)  iii)
iii) 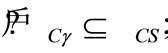 iv)
iv)  v)
v) 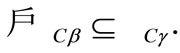
2) a) 
b) 
Corollary 3.5
1) a)  b)
b)  c)
c)  d)
d) 
2) a)  b)
b)  c)
c)  d)
d) 
Theorem 3.5 Let  for each
for each 
1) 
2) 
Proof. 1) Since  and
and  then
then  Thus
Thus

2) Since for every  then one can deduce that
then one can deduce that  for every
for every 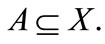 Also, since
Also, since  one can have that
one can have that  From Theorem 3.3 (2) we have
From Theorem 3.3 (2) we have

Corollary 3.6 For any
1) 

2) 

Remark 3.1 In crisp setting, i.e., if the underlying fuzzifying topology is the ordinary topology, one can have
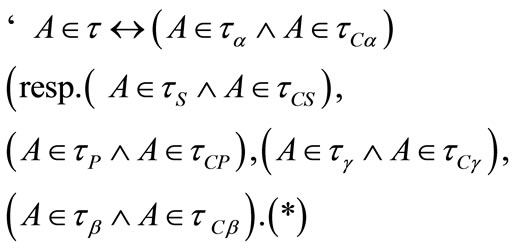
Of course the implication “®” in (*) is either the Łukaciewicz’s implication or the Boolean’s implication since these implications are identical in crisp setting. But in fuzzifying setting the statement (*) may not be true as illustrated by the following example.
Example 3.1 Let  and
and  be a fuzzifying topology on X defined as follows:'
be a fuzzifying topology on X defined as follows:'
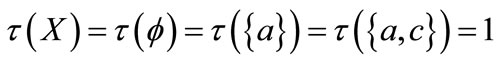 ;
;
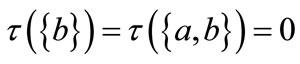 and
and 
From the definitions of the interior and the closure of a subset of X and the definitions of the interior and the closure of a fuzzy subset of X and some calculations we have:

and

So,
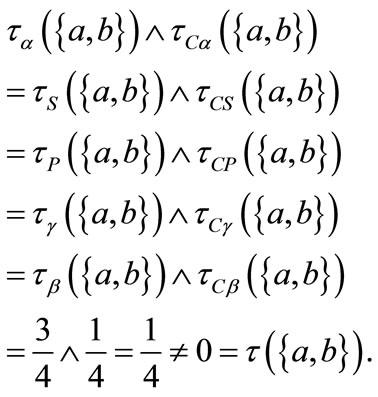
Theorem 3.6 Let  for each
for each  Then
Then
1) 
2) 
Proof. 1) It is obtained from Theorem 2.4 (1)(a) and (2)(a).
2) 

Corollary 3.7
1) 
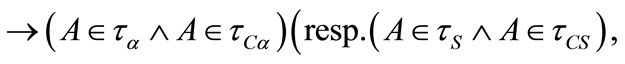


2) 


Theorem 3.7 Let  for each
for each  If for every
If for every ,
,  or
or  then
then
1) 
2) 
Proof. Using Theorem 3.6 it remains to prove the following
1) Suppose that  Then for each
Then for each  we have
we have  So
So
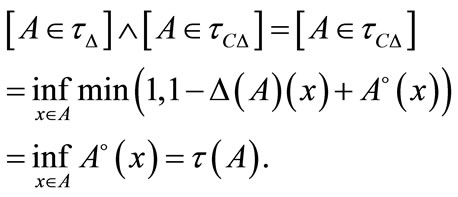
Now, suppose that  Since
Since , then
, then

For each  we have
we have  Thus,
Thus,

2) The proof is similar to 1).
Corollary 3.8 If for every 
 or
or  (resp.
(resp.  or
or 
 or
or 
 or
or  or
or  then
then
1) 

2) 

Theorem 3.8 Let  be a monotone. Then
be a monotone. Then

Proof.

First, we have 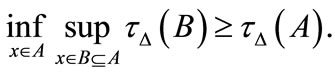 On the other hand, Suppose that
On the other hand, Suppose that  Then for any
Then for any  we have
we have  Since
Since  is monotone, then by Theorem 3.1 (2)(a) we have
is monotone, then by Theorem 3.1 (2)(a) we have
 By completely distributive law we have
By completely distributive law we have

Corollary 3.9

Remark 3.2 The following are valid in crisp setting:
1) 
2) 
3) 
but in fuzzifying setting these statement may not be true by the following example.
Example 3.2 From Example 3.1 we have
1) 

2) 
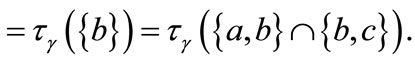
3) 

4. Fuzzifying Neighborhood Structure of a Point
In this section the concepts of ∆-neighborhood system and C∆-neighborhood system of a point are presented and a fuzzifying topology induced by C∆-neighborhood system is obtained.
Definition 4.1 The fuzzifying ∆-(resp. C∆-) neighborhood system of , denoted by
, denoted by 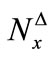 (resp.
(resp. )
) , is defined as follows:
, is defined as follows:

i.e.,
 .
.
Definition 4.2 Let .
.
1) If  (resp.
(resp. , the fuzzifying ∆-neighborhood system of
, the fuzzifying ∆-neighborhood system of  coincides with the fuzzifying (resp. fuzzifying
coincides with the fuzzifying (resp. fuzzifying  -, fuzzifying semi-, fuzzifying pre-, fuzzifying
-, fuzzifying semi-, fuzzifying pre-, fuzzifying  -, fuzzifying
-, fuzzifying  -) neighborhood system of
-) neighborhood system of  and will be denoted by
and will be denoted by  (resp.
(resp. );
);
2) If  (resp.
(resp.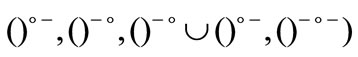 , the fuzzifying C∆-neighborhood system of
, the fuzzifying C∆-neighborhood system of  coincides with the fuzzifying
coincides with the fuzzifying  - (resp. fuzzifying csemi-, fuzzifying cpre-, fuzzifying
- (resp. fuzzifying csemi-, fuzzifying cpre-, fuzzifying  -, fuzzifying
-, fuzzifying  -) neighborhood system of
-) neighborhood system of  and will be denoted by
and will be denoted by  (resp.
(resp. ).
).
Theorem 4.1 Let ∆ be a monotone.
1) 
2) 
Proof. Using Theorem 3.8 we have

2) From 1) the proof is immediate.
Corollary 4.1 Let  be a fuzzifying topological space.
be a fuzzifying topological space.
1) 

1) 

Theorem 4.2 The mapping ,
,  , has the following properties:
, has the following properties:
1) If  is of type
is of type , then
, then  is normal for any
is normal for any ;
;
2) For any 
3) For any 
4) If  is monotone, then for any
is monotone, then for any 

5) If  is of type
is of type , then
, then

Proof. 1) Since  is of type
is of type , then
, then

2) If , then the results holds. Suppose
, then the results holds. Suppose . Then there exists
. Then there exists  such that
such that . Now, we have
. Now, we have  Thus
Thus 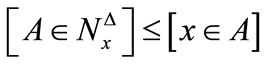 holds always.
holds always.
3) If , then the result holds. Now, suppose that
, then the result holds. Now, suppose that  Then we have
Then we have
 .
.
4) Since  is monotone, then from Theorem 4.1 a) we have
is monotone, then from Theorem 4.1 a) we have

5) 

Corollary 4.2 The mapping N

 has the following properties:
has the following properties:
1) For any ,
, 
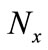 is normal;
is normal;
2) For any 

3) For any 

4) For any 

5) For any 

Theorem 4.3 The mapping 
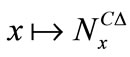 , has the following properties:
, has the following properties:
1) If  is of type
is of type , then
, then  is normal for any
is normal for any ;
;
2) For any 
3) For any 
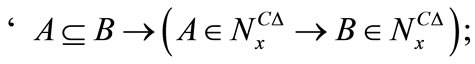
4) If  is monotone, then or any
is monotone, then or any 

Conversely, if a mapping  satisfies 1), 3) and 4), then it assigns a fuzzifying topology on X, denoted by
satisfies 1), 3) and 4), then it assigns a fuzzifying topology on X, denoted by , is defined as follows:
, is defined as follows:

Proof. Since  is normal and satisfies properties (2) and (3) in Theorem 4.2, then
is normal and satisfies properties (2) and (3) in Theorem 4.2, then  is a fuzzifying topology on
is a fuzzifying topology on . The rest of the proof is similar to the proof of Theorem 4.2.
. The rest of the proof is similar to the proof of Theorem 4.2.
Corollary 4.3 The mapping 

has the following properties:
1)  is normal for any
is normal for any ;
;
2) For any 

3) For any 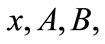

4) If 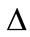 is monotone, then or any
is monotone, then or any 

5) The mapping  assigns a fuzzifying topology on X, denoted by
assigns a fuzzifying topology on X, denoted by 
 , is defined as follows:
, is defined as follows:

Theorem 4.4 If ∆ is of type  and monotone, then
and monotone, then 
Proof. Let  Then
Then

Corollary 4.4 1)  2)
2)  3)
3)  4)
4)  (5)
(5) 
5. Closure and Interior Operations in Fuzzifying Topology
The purpose of this section is to establish the concepts of fuzzifying ∆- and C∆-derived sets, fuzzifying ∆- and C∆-closure operation and fuzzifying ∆- and C∆-interior operation and study some of their properties.
Definition 5.1 The fuzzifying ∆- (resp. C∆-) derived set  (resp.
(resp. )
)  of
of  is defined as follows:
is defined as follows:

 i.e.,
i.e.,

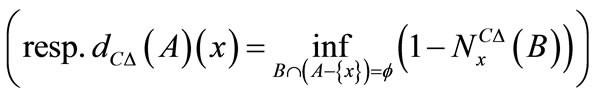 .
.
Definition 5.2 For
1) If  (resp.
(resp. , the notion of fuzzifying ∆-derived set of
, the notion of fuzzifying ∆-derived set of  coincides with the notion of fuzzifying derived (resp.
coincides with the notion of fuzzifying derived (resp.  - derived, semi-derived, pre-derived,
- derived, semi-derived, pre-derived,  -derived,
-derived, 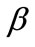 -derived) set and will be denoted by
-derived) set and will be denoted by
 ;
;
2) If  (resp.
(resp. , the notion of fuzzifying c∆-derived set of
, the notion of fuzzifying c∆-derived set of 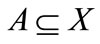 coincides with the notion of fuzzifying derived (resp.
coincides with the notion of fuzzifying derived (resp.  -derived, csemi-derived, cpre-derived,
-derived, csemi-derived, cpre-derived,  -derived,
-derived,  -derived) set and will be denoted by
-derived) set and will be denoted by
 .
.
Theorem 5.1 For every  we have
we have
1) 
2) 
Proof. 1) Using Theorem 4.3 3) we have

2) It is similar to the proof. of 1).
Corollary 5.1
1) a) 
b) 
c) 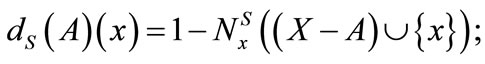
d) 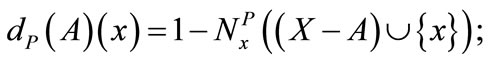
e) 
f) 
2) a) 
b) 
c) 
d) 
e) 
Theorem 5.2 For every  we have
we have
1) If ∆ is monotone, then 
2) If ∆ is of type  and monotone, then
and monotone, then
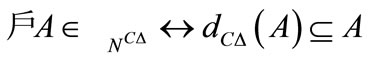 .
.
Proof. Using Theorem 4.1 (2) we have 1) 

2) It is similar to 1).
Corollary 5.2
1) a) 
b) 
c) 
d) 
e) 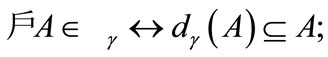
f) 
2) a) 
b) 
c) 
d) 
e) 
Definition 5.3 The fuzzifying ∆-(resp. C∆-) closure  (resp.
(resp.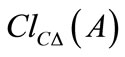 )
)  of
of  is defined as follows:
is defined as follows:

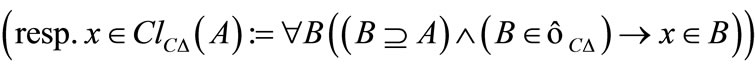 i.e.,
i.e.,

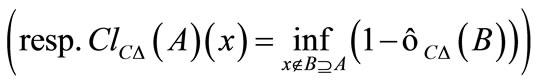 .
.
Definition 5.4 1) If  (resp.
(resp.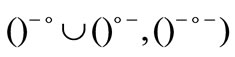
 , the notion of fuzzifying ∆-closure of
, the notion of fuzzifying ∆-closure of  coincides with the notion of fuzzifying closure (resp.
coincides with the notion of fuzzifying closure (resp.  -closure, semi-closure, pre-closure,
-closure, semi-closure, pre-closure,  -closure,
-closure,  -closure) operation and will be denoted by
-closure) operation and will be denoted by
 ;
;
2) If  (resp.
(resp. , the notion of fuzzifying C∆-closure of
, the notion of fuzzifying C∆-closure of  coincides with the notion of fuzzifying
coincides with the notion of fuzzifying  (resp. csemi, cpre,
(resp. csemi, cpre,  ,
, )-closure operation and will be denoted by
)-closure operation and will be denoted by
 .
.
Theorem 5.3 For every  we have
we have
1) 
2) 
Proof.
1) 

2) It is similar to the proof of (1).
Corollary 5.3
1) a) 
b) 
c) 
d) 
e) 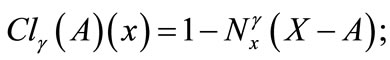
f) 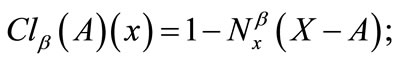
2) a) 
b) 
c) 
d) 
e) 
Theorem 5.4 For every  and
and  we have
we have
1) If ∆ is of type O1, then a) 
b) 
2) a) 
b) 
3) a) 
b) 
4) a) 
b) 
5) a) 
b) If ∆ is of type O1 and monotone, then

Proof. We prove only a) of each statements since b) is similar.
1) a) 

2) a) It is clear that  for any
for any  and
and  in case of
in case of  Now, suppose that
Now, suppose that  Then
Then  Therefore
Therefore
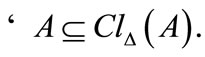
3) a) Using Theorem 5.1 (1) and (2) above, we have

4) a) 

5) a) Since  then from Theorem 5.2 (1) and (3) (a) above we have
then from Theorem 5.2 (1) and (3) (a) above we have

because  for any
for any 
Corollary 5.4
1) a) ; b)
; b)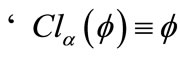 ; c)
; c)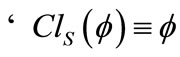 ; d)
; d) ; e)
; e) ; f)
; f) ; g)
; g) ; h)
; h) ; i)
; i) ; j)
; j) ; k)
; k)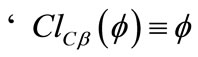 ;
;
2) for any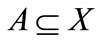 , a)
, a) ; b)
; b)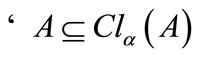 ; c)
; c) ; d)
; d) ; e)
; e) ; f)
; f) ; g)
; g) ; h)
; h) ; i)
; i) ; j)
; j) ; k)
; k) .
.
3) for any , a)
, a) ; b)
; b)  ; c)
; c) ; d)
; d) ; e)
; e) ; f)
; f) ; g)
; g)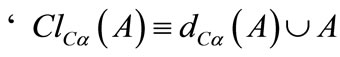 ; h)
; h) ; i)
; i) ; j)
; j) ; k)
; k) .
.
4) for any  and
and a)
a) ;
;
b) ;
;
c) ;
;
d) ;
;
e) ;
;
f) ;
;
g) ;
;
h) ;
;
i) ;
;
j) ;
;
k) .
.
5) for any a)
a)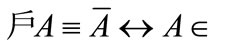 ;
;
b) ;
;
c)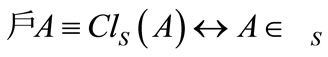 ;
;
d) ;
;
e)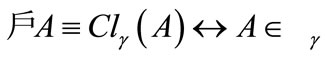 ;
;
f)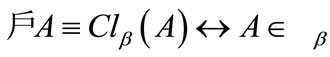 ;
;
g) ;
;
h) ;
;
i) ;
;
j) ;
;
k) .
.
Theorem 5.5 For every  we have
we have
1) 
2) 
Proof. 1) Suppose  Then
Then 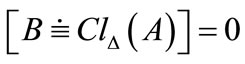 and the results holds. Now, suppose
and the results holds. Now, suppose 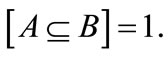 Then
Then  and
and  So
So

Let  Then
Then  For any
For any 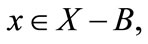
 , i.e., there exists
, i.e., there exists  such that
such that  and
and . Now we want to prove
. Now we want to prove . If not, then there exist
. If not, then there exist  with
with  Hence
Hence

and this is a contradiction. Therefore

Since t is arbitrary, it holds that 
2) The proof is similar to 1).
Corollary 5.5 For any A and B.
1) a) ;
;
b) ;
;
c) ;
;
d)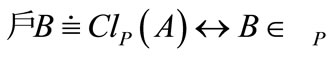 ;
;
e) ;
;
e) ;
;
2) a) ;
;
b) ;
;
c)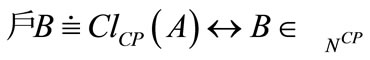 ;
;
d) ;
;
e) .
.
Definition 5.5 The fuzzifying ∆-(resp. C∆-) interior  (resp.
(resp. )
) 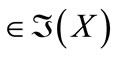 of
of  is defined as follows:
is defined as follows:
 .
.
Definition 5.6 1) If  (resp.
(resp.
 , the notion of fuzzifying
, the notion of fuzzifying  -interior of
-interior of  coincides with the notion of fuzzifying interior (resp.
coincides with the notion of fuzzifying interior (resp.  -interior, semi-interior, pre-interior,
-interior, semi-interior, pre-interior,  -interior,
-interior,  -interior) operation and will be denoted by
-interior) operation and will be denoted by
 ;
;
2) If  (resp.
(resp. , the notion of fuzzifying
, the notion of fuzzifying  -interior of
-interior of  coincides with the notion of fuzzifying
coincides with the notion of fuzzifying  (resp. csemi, cpre,
(resp. csemi, cpre,  ,
, )-interior operation and will be denoted by
)-interior operation and will be denoted by
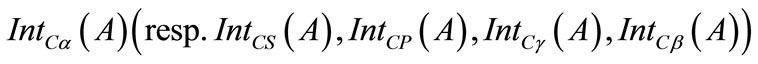 .
.
Theorem 5.6 For every  we have
we have
1) a) 
b) if  is of type O1 and monotone, then
is of type O1 and monotone, then

2) a) 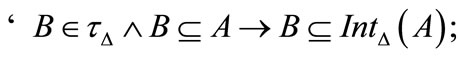
b) if  is of type O1 and monotone, then
is of type O1 and monotone, then

3) a) 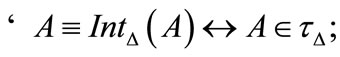
b) if  is of type O1 and monotone, then
is of type O1 and monotone, then

4) a) 
b) 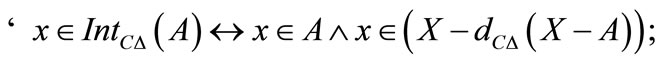
5) a) 
b) 
Proof. We prove only a) of each statements since b) is similar.
First, we prove 2) a) If  then
then  Now, suppose that
Now, suppose that  Then we have
Then we have
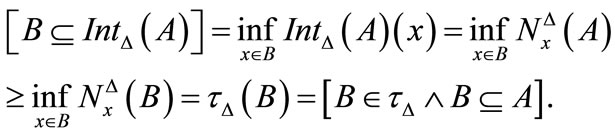
3) a) 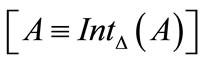

4) a) If 

If 

Thus 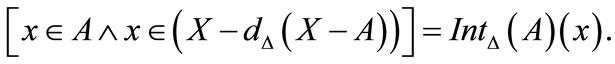
5) a) Follows from Theorem 5.3 (1).
Finally, we prove 1) a). From 5) a) and Theorem 5.5 1) we have

Corollary 5.6 For any 
1) a) ;
;
b) ;
;
c) ;
;
d) ;
;
e)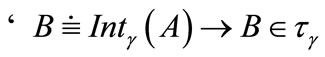 ;
;
f) ;
;
g) ;
;
h) ;
;
i) ;
;
j) ;
;
k)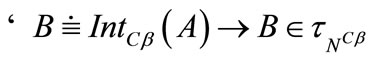 ;
;
2) a) ;
;
b) ;
;
c) ;
;
d) ;
;
e) ;
;
f) ;
;
g) ;
;
h)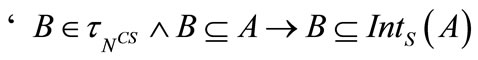 ;
;
i) ;
;
j) ;
;
k) ;
;
3) a) ;
;
b) ;
;
c) ;
;
d) ;
;
e)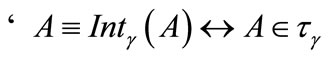 ;
;
f) ;
;
g) ;
;
h) ;
;
i) ;
;
j) ;
;
k) ;
;
4) a) ;
;
b) ;
;
c) ;
;
d) ;
;
e) ;
;
f) ;
;
g)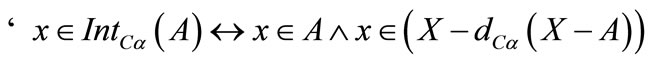 ;
;
h) ;
;
i) ;
;
j) ;
;
k) ;
;
5) a) ;
;
b) ;
;
c) ;
;
d) ;
;
e) ;
;
f) ;
;
g) ;
;
h)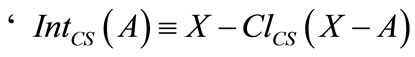 ;
;
i) ;
;
j) ;
;
k) .
.
6. Conclusions
The present paper investigates topological notions when these are planted into the framework of Ying’s fuzzifying topological spaces (in semantic method of continuous valued-logic). It continue various investigations into fuzzy topology in a legitimate way and extend some fundamental results in general topology to fuzzifying topology. An important virtue of our approach (in which we follow Ying) is that we define topological notions as fuzzy predicates (by formulae of Łukasiewicz fuzzy logic) and prove the validity of fuzzy implications (or equivalences). Unlike the (more wide-spread) style of defining notions in fuzzy mathematics as crisp predicates of fuzzy sets, fuzzy predicates of fuzzy sets provide a more genuine fuzzification; furthermore the theorems in the form of valid fuzzy implications are more general than the corresponding theorems on crisp predicates of fuzzy sets. The main contributions of the paper are to study some sorts of operations, called general fuzzifying operations. There are some problems for further study:
1) Apply the general fuzzifying operation to convergence theory, continuity, separation axioms etc.
2) What is the justification of these concepts in the setting of (2, L) topologies.