A Simple Encryption Keys Creation Scheme in Wireless Ad Hoc Networks ()
1. Introduction
The rapid progression of technology for mobile devices, including laptops and handheld computers, and the availability of inexpensive wireless networking hardware, has resulted in a great demand for wireless connectivity among mobile users. One approach to providing wireless connectivity is through the formation of a mobile ad hoc network (ad hoc, in Latin, means for this only).
A mobile ad hoc network (MANET) is a collection of mobile nodes that temporarily form a network. Such a network does not require the existence of the typical infrastructure underlying a network. Rather, each mobile node is equipped with a wireless interface that allows the node to communicate with other nodes via the wireless medium. Handheld computing devices and laptop computers with wireless transceivers are examples of mobile nodes that can come together to form a MANET. In a MANET, there is no central entity with the authority to administer the services and configurations of the network. All the nodes work collectively and cooperatively, in a distributed manner, to maintain the functions and services of the network. The distribution of responsibilities and tasks that are meant to keep the network running makes the network resilient to node failures. It also allows nodes to join and leave the network liberally without affecting the network’s operability. One important challenge that the MANETs still face is providing secure communication between the nodes of a MANET.
2. Motivation
Before we introduce any security primitives, services, components, or protocols into a system, that system should be well understood and characterized. The aim should be to deploy security mechanisms that practically and efficiently integrate with the core characteristics and functionalities of the system at hand. This emphasis should be applied when we try to secure the communications within a MANET. The bulk of the research on securing MANETs has focused on adapting security mechanisms that were designed and developed for conventional wired networks. This adaptation has resulted in security solutions that do not work efficiently or that make assumptions that are not aligned with the characterization of MANETs. In this paper, we propose the use of security mechanisms for MANETs that are designed based on the characteristics, functionalities, and goals of these networks.
The rest of this paper is organized as follows. In Section 3, we review the distinctive characteristics of ad hoc wireless networks. In Section 4, we elaborate on the requirements that must be fulfilled by candidate security frameworks for MANETs. A literature review of how to create encryption keys in the MANETs is presented in Section 5. The Diffie-Hellman key exchange [1], which is the basis for our proposed solution, is summarized in Section 6. Details of the proposed solution will be offered in Section 7. The paper is concluded in Section 8.
3. Characteristics of Mobile Ad Hoc Networks
MANETs have a number of distinctive characteristics that influence the design of security mechanisms to be utilized within them. In this section, we review some of these characteristics. A MANET is considered to be an autonomous self-organizing system of multiple mobile nodes that communicate wirelessly through the air. Nodes can join and leave the network at any time or at any state of the network. Additionally, nodes roam freely. There are no restrictions on the movements of the nodes. Such networks do not assume the existence of any supporting network infrastructure, nor do they require any prior setting up. The burden of providing networking services and functionality is handled cooperatively by the nodes of the network in a distributed fashion. We can summarize the discussed characteristics as follows [2]:
• Dynamic topologies of the network.
• Free mobility of the nodes.
• Limited processing power of the nodes.
• Limited storage capacity of the nodes.
• Limited power sources.
• No supporting infrastructure.
• No central authority to manage the network.
• No prior setting up.
• Distributed nature.
• Shared and open communication medium.
These characteristics should be taken into account while designing all the primitives, mechanisms, and protocols for securing the MANETs. Disregarding these characteristics or adapting modified ones may undermine the notion of an ad hoc network.
4. Security Requirements
Security frameworks for data communication must define a set of basic goals, services, and functionalities that enable the concerned parties to have secure communications. These services and functionalities constitute the building blocks for more complex security procedures and protocols. The frameworks in question should ensure that the requirements of Integrity, Confidentiality, Authentication, Non-repudiation, Availability, and Access Control are available to all communications [3-5]. Encryption is one of the key building blocks that facilitate the fulfillment of these requirements. We summarize the requirements as follows:
• Integrity:
Communicated information should be protected from modification or alteration and tampering should be detectable.
• Confidentiality:
Communicated information should be made accessible only to those who are authorized to receive it.
• Authentication:
The identities of the parties involved in the information exchange should be verifiable.
• Non-repudiation:
The actions of the parties involved in the information exchange should be undeniable.
• Availability:
The system resources or services should be available to legitimate users as and when needed.
• Access Control:
Unauthorized users should be prevented from accessing the system’s resources or services.
5. Key Management and Previous Works
Communicating entities are said to have a keying relationship when they share keying material to support cryptographic procedures [6]. Establishing and maintaining a keying relationship through well defined procedures and methods is called Key Management [6]. Establishing the encryption key is a two step process [6]. The first step is that all the parties involved should agree on the key. The second step is to distribute the key to all the parties involved. Maintaining the encryption key involves procedures such as renewing or revoking the key. Cryptography is the central issue in cryptosystems, and Key Management is at the heart of cryptography. The policies and procedures of a Key Management system depend, among other things, on whether the type of the keys is symmetric or asymmetric.
In designing Key Management schemes for MANETs, designers should optimize the computational complexity, processing requirements, and storage space associated with such schemes. This is due to the limited resources of the nodes of the MANETs. Another aspect worth considering has to do with the connectivity conditions between the nodes. A MANET may become partitioned because of the mobility of the nodes. Interference patterns between two nodes may make the link between them a unidirectional one. We believe that a decentralized, lightweight, peer-to-peer Key Management scheme is the most suitable scheme for a MANET.
Securing the MANETs is an active field of research. Many solutions have been proposed and published that have advocated different approaches, which are based on different mechanisms and techniques. In this review, we focus on the notable items of work that represent the approaches that have been proposed so far. The solutions presented in [7-11] have adapted the traditional approach for wired networks that is based on symmetric keys. These solutions require a pre-deployment setup process which is not a characteristic of true ad hoc networking. In another approach that utilizes asymmetric keys, which was originally designed for wired networks, the solutions presented in [12-14] involve a high level of processing and communications. These solutions stress the resources of the nodes. One of the first attempts to preserve the ad hoc nature of the MANETs was demonstrated in [15]. However, that solution requires the nodes to come within the transmission ranges of each other to establish a keying relationship. In our proposed technique, we do not have such a requirement.
6. Diffie-Hellman Key Agreement Protocol
The solution we propose is based entirely on the pioneering work presented in [1], and is known as the Diffie-Hellman key agreement protocol. It was the first practical key distribution and creation protocol that permitted two communicating entities to create a shared key by exchanging information through an open channel, without requiring any prior knowledge to be shared among them [6]. This solution is a perfect match for the issues involved in forming a MANET. The security of this protocol is based on the computational hardness of the Diffie-Hellman problem and its related problem of calculating discreet logarithms [6]. The Diffie-Hellman protocol works as follows:
Assumption
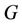is a finite cyclic group with a generator g.
A and B are two entities who want to establish a shared secret key.
Protocol Steps:
1) A secretly chooses integer
, at random, from the interval [0, |G| − 1].
2) B secretly chooses integer SB, at random, from the interval [0, |G| − 1].
3) A computes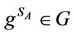
.
4) B computes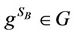
.
5) A sends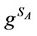 
to B.
6) B sends 
to A.
7) A computes
.
8) B computes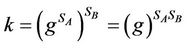
.
Since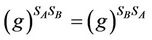
, it follows that it can be used as a shared secret key.
7. Our Proposed Solution
When node A (to be called the initiator node) of a MANET wants to establish a shared encryption key with node B (to be called the target node), it chooses a prime number p, a base b, and a secret integer SA. The initiator then calculates the value 
mod p. After that, the initiator unicasts a Key Creation Message (KC-Msg) to the target node. The KC-Msg contains VA, p, and b. Each node in the network maintains a simple data structure in the form of a table that is called a Keys Table (KT). The KT consists of two columns. The first column is called the Node ID, and the second is called the Key. The purpose of this table is to keep track of any shared encryption keys that have been established with other nodes. When the initiator node sends the KC-Msg, it creates a tentative entry in the KT with values “Target Node ID” and “NULL”, for Node ID and Key respectively.
Upon receiving the KC-Msg, the target node chooses a secret integer SB and calculates the value VB =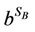 
mod p. The target node then calculates the shared encryption key K = 
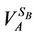mod p, and creates an entry in its KT with values “Initiator Node ID” and “K” for Node ID and Key, respectively. The final step of the protocol with respect to the target node is to send a Key Creation Response Message (KCR-Msg) that is unicasted to the initiator node. The KCR-Msg contains the VB.
When the initiator node receives the KCR-Msg, it calculates the shared encryption key K =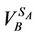 
mod p and updates the Key field in the entry corresponding to the target node in its local KT. At this point, both of the nodes are in a position to start exchanging encrypted message using the newly created shard encryption key.
7.1. Informal Description
Creating the encryption key between node A and B can be informally described as follows:
1) Node A chooses a prime number p, a base b, and a secret integer SA.
2) Node A calculates the value VA = 
mod p.
3) Node A sends the VA, p, and b to node B.
4) Node B chooses a secret integer SB.
5) Node B calculates the value VB =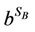 
mod p and sends it to A.
6) Node B calculates the shared encryption key K = 
mod p.
7) Node A calculates the shared encryption key K =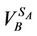 
mod p.
7.2. Formal Description
To describe the interaction between the nodes to create the key, we will follow the conventional notation that is found in the cryptography literature. When the goal of principle A (node A) is to create a shared key with principle B (node B), a message M (base b), a local secret key KA (secret integer SA), and modulus n (prime number p) are chosen such that M is a primitive root of n and M < n. Principle A then encrypts M using KA with an encryption technique based on the exponentiation algorithm (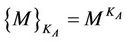
mod n). The original message M, the encrypted M, and the modulus n are sent from principle A to principle B.
1) A → B:
, n, M Upon receiving n and M, principle B chooses a local secret key KB and encrypts the message M with its own local key (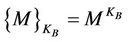
mod n), which it then sends it to principle A.
2) B → A: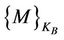 
At this point, both principles can locally calculate the shared KAB as follows:
3) In principle A KAB =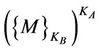 
mod n 4) While in principle B KAB = 
mod n Both principles will reach exactly the same shared key (KAB) with their local calculations. This is possible due the commutative property of exponentiation. That is,
mod n = 
mod n. This property also allows for the interaction to create the shared key, which can be initiated by either principle. For an eavesdropper, the shard key (KAB) is derived from known message (M) and modulus (n) but unknown local secret keys. If we use a very large prime for n and large numbers for KA and KB, it would be impossible to calculate the local keys of A and B.
7.3. Simple Example
We will illustrate how the protocol works with the following example:
1) Node A chooses p = 31, b = 3, SA = 4.
2) Node A calculates VA = 34 mod 31 = 19.
3) Node A sends VA = 19, p = 31, and b = 3 to node B.
4) Node B chooses SB = 8.
5) Node B calculates VB = 38 mod 31 = 20; and sends it to node A.
6) Node B calculates K =198 mod 31 = 9.
7) Node A calculates K = 204 mod 31= 9.
7.4. Evaluation and Threats
Based on the previous description of our solution, creating the key would require the exchange of just two messages (KC-Msg and KCR-Msg). It would also require each node to maintain a very simple data structure (the Keys Table KT). We kept the requirements at a minimum to allow the solution to be efficiently used in MANETs.
The Diffie-Hellman protocol that we employed is primarily subject to two types of attacks: brute force and man-in-the-middle attacks. In a brute force attack, an attacker may exhaustively try all possible keys to decrypt an encrypted message. In [16], successfully performing such an attack would be equivalent to solving the discrete logarithm problem. This is a difficult problem. In a man-in-the-middle attack, a third malicious entity presents itself as a legitimate entity in the protocol exchange. For example, a malicious principle C can pretend to be principle B with regard to the exchange with principle A and pretend to be A with regard to B. This attack can be countered by utilizing the types of authentication services or protocols that are described in [17,18]. However, designing a new protocol for authentication that follows the principle of ad hoc wireless networking emphasized in this paper would be desirable. This is the next step in our future work.
8. Conclusion
In this paper, we introduced an encryption keys creation technique for MANETs based on The Diffie-Hellman key exchange. The technique is simple and preserves the ad hoc nature of MANETs. By publishing this work, we are trying to initiate a paradigm shift in securing MANETs. In the new paradigm that we are proposing, the focus should be on building security primitives purposely for MANETs, and not on adapting primitives that were meant for conventional wired networks.