Wronskian and Grammian Solutions for Generalized (n + 1)-Dimensional KP Equation with Variable Coefficients ()
1. Introduction
Recently, there has been a growing interest in studying variable-coefficient nonlinear evolution equations (NLEEs). Quite a few researchers studied the variable-coefficient KP equations [1-3], which provides us with more realistic models in such physical situations as the canonical and cylindrical cases, propagation of surface waves in large channels of varying width and depth with nonvanishing vorticity and so on. In this paper, we consider the generalized variable-coefficient (n + 1)-dimensional KP equation
(1)
where
, 
are arbitrary functions with respect to t. Equation (1) can be reduced to the (3 + 1)-dimensional KP equation
(2)
by setting
Equation (2) describes the dynamics of solitons and nonlinear waves in plasmas physics and fluid dynamics. Obviously, (1) is the generalization of (2).
It is well known that the bilinear method first proposed by Hirota provides us with a comprehensive approach to construct exact solutions [4-6]. Once a NLEE is written in bilinear form, we are able to derive systematically particular solutions including the multi-soliton solutions. Soliton solutions can also be written in Wronskian form, which was first introduced by Satsuma in 1979 [7]. Freeman and Nimmo developed the Wronskian technique, which admits direct verifications of solutions in Wronskian form to the bilinear equations [8]. It is noted that Grammian is another type of solution representation for soliton equations, which can be rewritten as a Pfaffian and the proof can easily be completed by virtue of Pfaffian properties [9,10].
The organization of the paper is as follows. In Section 2, based on the Hirota bilinear method, we obtain the bilinear forms of (1). Then the Wronskian and Grammian solutions of (1) are derived in Sections 3 and 4, respectively. Finally, the conclusions and discussions will be given in Section 5.
2. Bilinear Form of (1)
By the dependent variable transformation
(3)
equation (1) can be transformed into the following bilinear form:
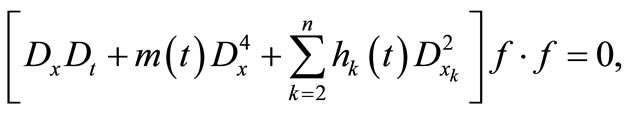(4)
where the Hirota bilinear operators 
and 
are defined by
(5)
Equation (4) can be rewritten as
(6)
3. Wronskian Solution of (1)
In this section, the N-soliton solutions of (1) in Wronskian form have been generated.
Theorem 1. Equation (4) has the solution in terms of the Wronskian determinant
(7)
where 
and 
satisfy the set of linear partial differential equations
(8)
Proof. To conveniently write (7), we adopt the compact notation
(9)
Under the properties of the Wronskian determinant and the conditions (8), we obtain
(10)
Substituting these derivatives into (6), the left side becomes
(11)
Thus, we have the N-soliton solutions of (1) in Wronskian form
(12)
where 
satisfies the conditions (8).
4. Grammian Solution of (1)
In what follows, we focus on the Grammian type solution and construct a broad set of sufficient conditions which make the Grammian determinant a solution of the bilinear Equation (4).
Theorem 2. Equation (4) has the Grammian solution as follows:
(13)
where the functions 
and 
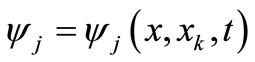satisfy the two sets of conditions
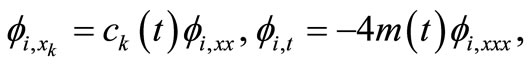(14)
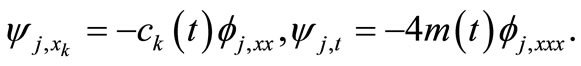(15)
Proof. A differential of the determinant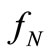 
expressed by means of a Pfaffian is
(16)
Next we introduce the Pfaffians 
defined by
(17)
(18)
Based on the Pfaffians defined above, differentials of the elements 
can be obtained as follows:
(19)
We denote
, then
(20)
Substituting the above Pfaffians into (4), after some calculations, we have
(21)
This shows that the Grammian determinant 
with the conditions of (14) and (15) solves (4).
5. Conclusions and Discussions
In summary we have extended the Wronskian method and Pfaffian properties to the generalized variable-coefficient (n + 1)-dimensional KP equation (1). As a result, the Wronskian solutions and the Grammian solutions of (1) have been derived. It is known that if one gets the solutions of the conditions (8) or that of (14) and (15), then one can obtain the corresponding solutions of (1), which need to be further studied.
6. Acknowledgements
This work is supported by the National Natural Science Foundation of China (No 10771196 and No 10831003), the Foundation of Zhejiang Educational Committee (No. Y201018244) and Zhejiang Innovation Project (No T200905).