A Note on the Self-Consistency of the Dirac Equation

Rajat Roy

Department of Electronics and Electrical Communication Engineering, Indian Institute of Technology, Kharagpur, India.

DOI: 10.4236/oalib.1106428                

Abstract

The Dirac equation of relativistic quantum mechanics is critically examined to see that it gives self-consistent results. Our findings are in the negative.

Keywords

Dirac Equation, Anti-Commutation, Self-Consistency

1. Introduction

The relativistic formulation of quantum mechanics for particles with spin half is made with the help of the Dirac equation. However the present author feels that certain consistency checks are needed to see if all the predictions of this equation do not lead to any contradictory results. With this view a few years back [1] we studied the Lorentz transformation properties of zitterbewegung terms which arises while constructing wave packets for the electron. In this note, we study the self consistency properties of a free Dirac particle wave function under an extreme condition when its velocity approaches that of light.

2. The Eigen States of the Dirac Hamiltonian for a Particle with Almost Luminal Velocities

The Dirac formulation of relativistic quantum mechanics introduces some new operators ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and $\beta$. We can write the equation in the form [2] (see Equation (1.13) of this famous book)

$i\hslash \frac{\partial \psi }{\partial t}=\frac{\hslash c}{i}\left({\alpha }_1\frac{\partial \psi }{\partial x^1}+{\alpha }_2\frac{\partial \psi }{\partial x^2}+{\alpha }_3\frac{\partial \psi }{\partial x^3}\right)+\beta m{c}^2\psi$. (1)

here the operator on the right hand side is identified as the Hamiltonian

$H\equiv \frac{\hslash c}{i}\left({\alpha }_1\frac{\partial }{\partial x^1}+{\alpha }_2\frac{\partial }{\partial x^2}+{\alpha }_3\frac{\partial }{\partial x^3}\right)+\beta m{c}^2$ (2)

A free particle wave function like that of an electron moving in the $x^1$ -direction (here $x^1,x^2,x^3$ can be identified with the coordinates $x,y,z$ commonly used) that is for which $\frac{\partial \psi }{\partial x^2}$ and $\frac{\partial \psi }{\partial x^3}$ are zero can be written as

$\psi \left(x^1,t\right)=\left[\begin{array}{c}\cosh \frac{\omega }{2}\\ 0\\ 0\\ -\sinh \frac{\omega }{2}\end{array}\right]{\text{e}}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }$ (3)

where E and $p_{x1}$ are constants the energy and momentum of the particle respectively and $\omega$ is related to its velocity (speed) v by the relation

$\tanh \omega =-\frac{v}{c}$. That Equation (3) is indeed a solution can be checked by verifying

that it satisfies Equation (1). It can also be obtained by means of Lorentz transformation properties of spinor as described in chapter 3 of ref. [2]. Thus $\psi \left(x^1,t\right)$ is an eigen state of the Hamiltonian H with eigen value E if we remember the classical relations $E=m{c}^2\cosh \omega$ and $p_{x1}=-mc\sinh \omega$. This is true for any value of $\omega$ for example when $\omega \to -\infty$ that is when $v\to c$. Thus we write for the limiting state

$H\underset{v\to c}{\lim }\psi \left(x^1,t\right)=\underset{v\to c}{\lim }E\psi \left(x^1,t\right)$ (4)

It is also possible to check that $\underset{v\to c}{\lim }\psi \left(x^1,t\right)$ is an eigen state of the operator ${\alpha }_1$ with eigen value 1 since we have the limiting relation $\underset{\omega \to -\infty }{\lim }\frac{\cosh \frac{\omega }{2}}{-\sinh \frac{\omega }{2}}=1$. Thus

$\begin{array}{l}{\alpha }_1\underset{\omega \to -\infty }{\lim }\left[\begin{array}{c}\cosh \frac{\omega }{2}\\ 0\\ 0\\ -\sinh \frac{\omega }{2}\end{array}\right]{\text{e}}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }\\ =\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right]\underset{\omega \to -\infty }{\lim }\left[\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right]\cosh \frac{\omega }{2}{e}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }\\ =\underset{\omega \to -\infty }{\lim }\left[\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right]\cosh \frac{\omega }{2}{\text{e}}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }\end{array}$ (5)

here we disagree with Bjorken and Drell that the eigen functions of $c\stackrel{\to }{\alpha }$ can be constructed by including both positive and negative energy solutions only (see p. 37 of ref. [2]) and not otherwise. The referee has asked us to elaborate on this disagreement and so we quote the passage from the book “Indeed in constructing eigenfunctions of $c\stackrel{\to }{\alpha }$ we have to include both positive and negative energy

solutions, since the eigenvalues of $c{\alpha }^i$ are $\pm c$ whereas $\left|{\langle c{\alpha }^i\rangle }_{+}\right|<c$, according to (3.29).” Let us first state that not only $\left|{\langle c{\alpha }^i\rangle }_{+}\right|<c$ but also $\left|{\langle c{\alpha }^i\rangle }_{-}\right|<c$ since ${\langle c\stackrel{\to }{\alpha }\rangle }_{-}={\langle \frac{c^2\stackrel{\to }{p}}{E}\rangle }_{-}$ as they are material particles or antiparticles. Furthermore the velocities of these particles and antiparticles can approach the velocity

of light in vacuum as closely as possible if we increase their respective energies indefinitely. The meaning of eigen states of $c{\alpha }^i$ are such states whose expectation values of the velocity operator $c{\alpha }^i$ closely approach $\pm c$ and not that they

are exactly equal to $\pm c$. Let us take the example of ${\alpha }_1=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right]$ with the eigen states $\left[\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right]$, $\left[\begin{array}{c}0\\ 1\\ 1\\ 0\end{array}\right]$, $\left[\begin{array}{c}1\\ 0\\ 0\\ -1\end{array}\right]$, $\left[\begin{array}{c}0\\ 1\\ -1\\ 0\end{array}\right]$ and with the respective eigen values 1,

1, −1, −1. Wave functions of material particles and antiparticles as we have explicitly demonstrated in the case of Equation (5) can approach one of these eigen states and hence they should be considered as eigen function of energy as well (besides that of being eigen functions of ${\alpha }_1$ ) if the concept of limit has any meaning. The present author also feels that wave functions consisting of positive and negative energy solutions that is states where particles and antiparticles are combined together into one packet can approach such an eigen state only in a limiting sense as we demonstrate now. Take for example the superposition of positive and negative energy solution

$\left[\begin{array}{c}A\cosh \frac{\omega }{2}{\text{e}}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }-B\sinh \frac{\omega }{2}{e}^{iEt/\hslash -i{p}_{x1}{x}^1/\hslash }\\ 0\\ 0\\ -A\sinh \frac{\omega }{2}{\text{e}}^{-iEt/\hslash +i{p}_{x1}{x}^1/\hslash }+B\cosh \frac{\omega }{2}{\text{e}}^{iEt/\hslash -i{p}_{x1}{x}^1/\hslash }\end{array}\right]$ which can be considered an eigen

function of ${\alpha }_1$ provided the space and time variations of the two nonzero entries in this column vector approach each other that is if $A=\pm B$ or if either A or B is zero. Also more importantly when both A and B are present and when

$A=B$ say then we must have $\cosh \frac{\omega }{2}=-\sinh \frac{\omega }{2}$ that is $\omega \to -\infty$ but this

however is not an eigen state of energy. The question that whether it is possible to put $\omega$ exactly equal to $-\infty$ and to which we would like to give a negative response is because of the fact that the quantity E whatever be its physical meaning now is again infinity. Since Bjorken and Drell has only made a statement without showing us a method to construct an eigen function (of $c{\alpha }^i$ ) I hope my arguments will be accepted.

From Equations (4) and (5) we obtain

$\left(H{\alpha }_1-{\alpha }_{1}H\right)\underset{v\to c}{\lim }\psi \left(x^1,t\right)=\underset{v\to c}{\lim }\left(E\psi \left(x^1,t\right)-E\psi \left(x^1,t\right)\right)=0$ (6)

A direct evaluation on the other hand of the commutator $\left[H,{\alpha }_1\right]=H{\alpha }_1-{\alpha }_{1}H$ using the (anti) commutation relations Equation (1.16) of ref. [2] shows that

$\begin{array}{c}\left[H,{\alpha }_1\right]=\frac{\hslash c}{i}\left(\left[{\alpha }_2,{\alpha }_1\right]\frac{\partial }{\partial x^2}+\left[{\alpha }_3,{\alpha }_1\right]\frac{\partial }{\partial x^3}\right)+m{c}^2\left[\beta ,{\alpha }_1\right]\\ =\frac{\hslash c}{i}\left(2{\alpha }_2{\alpha }_1\frac{\partial }{\partial x^2}+2{\alpha }_3{\alpha }_1\frac{\partial }{\partial x^3}\right)+2m{c}^2\beta {\alpha }_1\end{array}$ (7)

If this expression is made is made to operate on $\psi \left(x^1,t\right)$ in the appropriate limit we get $\left[H,{\alpha }_1\right]\underset{v\to c}{\lim }\psi \left(x^1,t\right)=\underset{v\to c}{\lim }2m{c}^2\beta {\alpha }_1\psi \left(x^1,t\right)\ne 0$ which directly contradicts Equation (6) and hence is a self contradiction of the Dirac formulation of quantum mechanics. The reason for this is that the formulation contains unwanted operators.

3. Concluding Remarks

The Dirac equation can be made self consistent by abandoning the correspondence relations with classical relativistic mechanics $E=m{c}^2\cosh \omega$ and 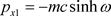. In this way, some changes in the values of 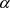-s and 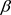may help in maintaining the forms of Equation (1) and as well as that of the solution that is Equation (3). But then it necessitates that a new meaning be given to the constants E and 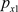and also the anti-commutation relation 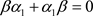will have to be given up leading to a complete break with the Klein-Gordon equation. One has to make a formulation and show in practice the results that it will lead to.

Acknowledgements

We would like to thank our Institute for providing funds with which the publication cost of this paper was met. Also we thank the referee for the constructive comments.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Roy, R. (2017) Lorentz Transformation Properties of Currents for the Particle-Anti- particle Pair Wave Functions. Open Access Library Journal, 4, e3730. https://doi.org/10.4236/oalib.1103730
[2]	Bjorken, J.D. and Drell, S.D. (1964) Relativistic Quantum Mechanics. McGraw-Hill, New York.