Relativistic Formulae for the Biquaternionic Model of Electro-Gravimagnetic Charges and Currents ()
1. Introduction
The mathematical representation of physical processes in various media is always connected with the choice of the coordinate system. For example, the coordinates of vectors, gradients, and rotors of physical fields change by transfer from one coordinate system to another. Therefore, in the construction of mathematical models of physical processes, in addition to the various equations and relationships which connect their physical characteristics in some coordinate system, the laws of transformation of these quantities and relations must be determined when passing from one coordinate system to another.
The most common one is the Cartesian coordinate system. Since its choice in Euclidean space is quite arbitrary both with respect to the origin of coordinates and with respect to the orientation of its base frames, therefore, for any mathematical model it is necessary to determine the transformation formulas of all relations and magnitudes for orthogonal group of coordinate transformations and for frame shift. It is well known that the equations of motion of homogeneous media in Newtonian mechanics are invariant with respect to these transformations and Galilean transformations in coordinate systems moving relative to each other at a constant speed in a fixed direction. For isotropic media, the equations of motion even retain their form, for anisotropic media they are transformed in accordance with the rules of tensor analysis.
However in dynamics of electromagnetic media these properties don’t remain. In particular, H.A. Lorentz proved that Maxwell equations are not invariant under Galilean transformation, and he constructed the linear transformation keeping their invariance in Minkowski space [1] . This transformation began to be called Lorentz’s transformation, and transformation formulae (relativistic formulae) have formed the basis of the relativity theory of A. Einstein. Poincare, investigating Maxwell’s equations, constructed the group of linear transformations keeping their invariance in Minkowski space [2] . They represent superposition of orthogonal transformations and Lorentz’s transformation.
In the real work the biquaternionic model is considered, which is earlier offered by the author for electro-gravimagnetic (EGM) fields, charges and currents, and their invariance relative to the group of Poincare-Lorentz transformations on Minkowski space is investigated.
In the papers [3] [4] the biquaternionic model of electro-gravimagnetic (EGM) field has been considered which is designated as biquaternionic A-field. For this the Hamilton form of Maxwell’s equations has been used [5] and its quaternionic record [6] . Based on the hypothesis of a magnetic charge, it’s carried out field complexification with the introduction of the gravimagnetic density to the Maxwell equations. The closed system of equations of EGM-charges and currents interaction has been constructed, which is the field analogue of the three famous Newton’s laws for mechanics of material points.
Here we prove an invariance of these equations with respect to Poincare-Lo- rentz transformation. We obtain the relativistic formulas for the densities of electric and gravimagnetic charges and currents, active power and forces by their interaction. At first we give some definitions of differential algebra of biquaternions, for not to refer the reader to other author’s works to read this article. Then we consider how biquaternionic differential operators-mutual bigradients are changing by these transformations. After that we’ll consider equations of EGM-charge and current transformation under action of external EGM-field and construct relativistic formulas for all introduced values.
2. Biquaternions in the Minkowski space Some Definitions and Designations
We consider the linear functional space of biquaternions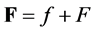 , where
, where  is complex function ,
is complex function ,  is complex vector-function on Minkowski space
is complex vector-function on Minkowski space . It is linear space:
. It is linear space:
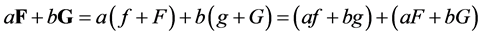 (1.1)
(1.1)
with the known operation of quaternionic multiplication
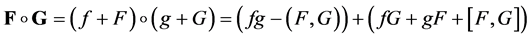 (1.2)
(1.2)
Here scalar product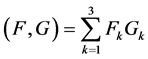 , vector product
, vector product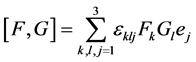 ,
, 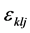 is Leavy-Chivitta symbol,
is Leavy-Chivitta symbol,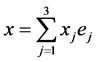 . We use the following notations.
. We use the following notations.
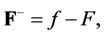
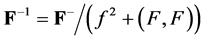
when it exists.
Complex conjugate Bq. to  is
is
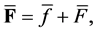
where the bar over symbol denotes the complex conjugate number.
Unitary Bq  if
if 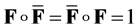 .
.
Conjugate Bq.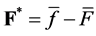 . If
. If 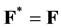 , then
, then ![]() is self-conjugated Bq.
is self-conjugated Bq.
Scalar production of biquaternions is the bilinear operation
![]()
The norm of ![]() is
is
![]()
The pseudo norm of ![]() is
is
![]()
We use biquaternionic differential operators which are named mutual bigradients:
![]()
![]()
![]()
Here![]() . Their superposition has the useful property:
. Their superposition has the useful property:
![]() (1.3)
(1.3)
where ![]() is classic wave operator (d’alambertian).
is classic wave operator (d’alambertian).
3. The Poincare-Lorentz Transformation on M
We can quaternize Minkowski space if to enter complex conjugate Bqs:
![]()
They are self-conjugated:
![]()
and
![]() (3.1)
(3.1)
If to enter the Bqs
![]()
![]()
![]()
then we have the biquaternionic form of Lorentz transformation
![]() (3.2)
(3.2)
This implies
![]() (3.3)
(3.3)
![]()
If to denote
![]() (3.4)
(3.4)
then we have well known formulas of
Lorentz transformation:
![]() (3.5)
(3.5)
![]()
which corresponds to the motion of the system in the direction of the vector ![]() with a dimensionless velocity
with a dimensionless velocity![]() .
.
The pseudo norm is preserved as
![]()
Similarly, with the help of conjugated biquaternions
![]()
![]()
we can write a group of orthogonal transformations on the vector part of![]() :
:
![]() (3.6)
(3.6)
This implies
![]()
![]()
It is the turn of ![]() around the vector
around the vector ![]() at the angle
at the angle![]() . The time
. The time ![]() does not change. This transformation preserves the norm and the pseudo-norm
does not change. This transformation preserves the norm and the pseudo-norm![]() .
.
Lemma1. Poincare-Lorentz transformation on ![]() has the form:
has the form:
![]() (3.7)
(3.7)
It is equal to
![]() (3.8)
(3.8)
and
![]()
Proof. By use of associativity of biquaternionic product we have
![]()
![]()
After calculating the scalar and vector part we obtain (3.8). Here the unit vector ![]() determines the direction of motion of the new coordinate system, and other parameters define the speed of motion and the angle of rotation, as has been shown above.
determines the direction of motion of the new coordinate system, and other parameters define the speed of motion and the angle of rotation, as has been shown above.
4. Biquaternionic Representation of EGM-Field Characteristics
For EGM-field description we entered next biquaternions [3] [5] :
EGM-potential ![]()
EGM-intensity ![]()
Charge-current ![]()
Energy-impulse of EGM-field
![]()
Here ![]() is the complex vector-function of intensities of EGM-field:
is the complex vector-function of intensities of EGM-field:
![]()
where ![]() are the electric and gravimagnetic field intensities,
are the electric and gravimagnetic field intensities, ![]() are the constants of electrical conductivity and magnetic permeability. The potential part of the vector
are the constants of electrical conductivity and magnetic permeability. The potential part of the vector ![]() describes the intensity of the gravitational field, and the vortex part defines the magnetic field.
describes the intensity of the gravitational field, and the vortex part defines the magnetic field.
The charge density of the EGM-field ![]() is expressed in terms of the electric charge density
is expressed in terms of the electric charge density ![]() and the gravymagnetic mass density
and the gravymagnetic mass density![]() :
:
![]() (4.1)
(4.1)
Electro-gravimagnetic current ![]() is expressed in terms of the electric current density (
is expressed in terms of the electric current density (![]() ) and it gravymagnetic current density (
) and it gravymagnetic current density (![]() ):
):
![]() (4.2)
(4.2)
The equation of EGM field has the form
Maxwell equation
![]() (4.3)
(4.3)
It shows that the charge-current is physical appearance of the bigradient of EGM-intensity.
If bigradient of EGM-intensity is equal to zero then there are not charges and currents. But EGM-intensity isn’t equal zero by this; it is the solution of homogeneous Equation (4.3) with zero right part.
The equation of the EGM-field (4.3) allows to determine the charges and currents if the intensity is known. Vice versa, it gives possibility to find the field intensities as a solution of certain boundary-value problems by known charges and currents. That is they are a single system “field-substance-field”, mutually generating each other.
The other biquaternions of the EGM-field are connected by the following relations
![]()
The Equation (4.3) is generalization of biquaternionic form of Maxwell equation for which![]() . In this case potential must to satisfy to the Lorentz gauge:
. In this case potential must to satisfy to the Lorentz gauge:
![]()
then ![]() and
and
![]()
In this case from the scalar part of the last equation we obtain the
Charge conservation law
![]() (4.4)
(4.4)
By this cause we name Eq. (4.3) the Maxwell equation.
5. Poincare-Lorentz Transformation of Mutual Bigradients
At first we define how the mutual complex gradients of the biquaternion are transformed under the Poincare-Lorentz transformations from ![]() to
to![]() .
.
In the new coordinates system ![]()
Lemma 5.1. If
![]()
then
![]() (5.1)
(5.1)
Proof. Using the differentiation rules according to (3.8), we have
![]() (5.2)
(5.2)
These relations coincide with (3.8) upon replacement![]() , which corresponds to the first formula (5.1). The second formula of the lemma is proved similarly.
, which corresponds to the first formula (5.1). The second formula of the lemma is proved similarly.
6. Charges-Currents Interaction Equations
To describe the interaction between two systems of charges and currents ![]() we introduced in [4] [7] the biquaternions of
we introduced in [4] [7] the biquaternions of
Power-force
![]()
Vector parts of these Bqs describe the forces of external EGM-field. Scalar parts describe the power of these forces.
Changing the charge-currents under the influence of the electro-gravimag- netic field of other charges and currents is described by the following system:
Law of charges-currents interactions
![]()
![]()
![]()
Here the constant ![]() is introduced by cause the physical dimension of left and right part.
is introduced by cause the physical dimension of left and right part.
Two first equations correspond to the second Newton’s law, second one - to the third Newton’s law (the action is equal to the contraction). Together with the last Maxwell equations for A-fields, they give the closed system of differential equations for the determination of charge-currents transformation by their interaction.
We note that in the case of absence of external fields (![]() ) we have from here:
) we have from here:
Free ![]() -field equations
-field equations
![]() (6.1)
(6.1)
This system gives possibility to construct charges, currents and intensities of free EGM-fields (see [3] ).
7. Relativistic Formulas for Charges and Currents
The invariance of the quaternionic forms of Maxwell equations with respect to the group of Poincare-Lorentz transformations has been well known [7] [8] [9] . We’ll show that the equations of charge-current transformation are invariant under these transform and obtain relativistic formulas for all physical values in these equations.
Theorm 7.1. After Poincare-Lorentz transformation on M, the ![]() -transfor- mation equation retains the form:
-transfor- mation equation retains the form:
![]() (7.1)
(7.1)
where
![]()
Proof. Following Lemma 4.1, using the associativity of the product, we obtain these formulae:
![]()
![]() by analogy
by analogy ![]() (3.7) by use (4.1) we get
(3.7) by use (4.1) we get
![]() (7.2)
(7.2)
If to calculate ![]() by analogy
by analogy ![]() (3.7) by use the property of complex conjugated values:
(3.7) by use the property of complex conjugated values:
![]()
we get by use (7.1)
![]()
![]()
Defining the scalar and vector parts of the corresponding biquaternions, we obtain relations for charge and current densities and for power and force. The theorem has been proved.
If ![]() is an orthogonal transformation, then we obtain the usual recalculation of the coordinates of the vector part of biquaternions for orthogonal transformations. In this case, the scalar parts of the biquaternions (the charge and mass density and the power of the acting electric and gravimagnetic forces) do not change:
is an orthogonal transformation, then we obtain the usual recalculation of the coordinates of the vector part of biquaternions for orthogonal transformations. In this case, the scalar parts of the biquaternions (the charge and mass density and the power of the acting electric and gravimagnetic forces) do not change: ![]()
If ![]() is classic Lorentz transformation (3.2) then from this theorem, with allowance for (3.4), it follows the next.
is classic Lorentz transformation (3.2) then from this theorem, with allowance for (3.4), it follows the next.
Relativistic formulae for charge and current:
![]()
By use (3.5) we get
Relativistic formulae for power and force:
![]()
![]()
We will write these relations separately for the real and imaginary components of charges and currents, taking into account the notations introduced in point 4. From the real part, we obtain the Lorentz transformation formulae for the densities of electric charge and electric current:
Relativistic formulae for electric and gravimagnetic charge and current:
![]()
![]()
We notice that in the formula of transformation of gravimagnetic mass density the first composed gives Einstein increasing in mass in mobile system of coordinates and tends to infinity by![]() . The second summand can it both to increase, and to reduce, depending on the direction of electric current. The vertical to e components of electric and gravimagnetic currents don’t change, but horizontal parts increase by
. The second summand can it both to increase, and to reduce, depending on the direction of electric current. The vertical to e components of electric and gravimagnetic currents don’t change, but horizontal parts increase by ![]() and also tend to infinity.
and also tend to infinity.
8. Conclusion
The field of EGM charges-currents in the absence of external fields is called free field. In article [3] the author constructed analytical solutions of Equation (6.1) of a free field for charges-currents (F = 0). Using these decisions in relativistic formulae, it’s possible to consider as the electric and gravimagnetic charges and currents will be transformed at these transformations. In articles [10] [11] the author obtained the analytical solutions of a biquaternionic form of the generalized Dirac’s equation which presents special cases of the equation of transformation of charges-currents in the stationary uniform external EGM-field. These decisions can also be used in relativistic formulae. Analyzing these expressions, it is possible to receive the curious conclusions that we offer the interested reader.
The purpose of this article is the proof of invariance of A-field equations concerning group of Poincare-Lorentz transformations and creation of relativistic formulae. It means mathematical justifiability of this model and its adequacy to the existing physical ideas about matter, space, time.