Transformation of CSD When Crystal Shape Changes with Crystal Size into CLD from FBRM by Using Monte Carlo Analysis ()
1. Introduction
Inmanufacturing process of crystal, powder, or granule products, it is necessary to measure change in CSD (crystal size distribution) or PSD (particle size distribution) with time accurately because CSD is one of the most important indices that evaluate quality of products [1] .
FBRM (focused beam reflectance measurement) can measure CLD (chord length distribution) in line, but it is well known that CLD is different from CSD because of principle of FBRM [2] [3] . In FBRM, focused beam from probe enters suspension in vessel, and chord length is measured based on detection time of backscattered light when beam runs cylindrically at high speed. Back scattered light results from beam which hits a crystal, but the chord length can differ from the crystal size because the beam doesn’t necessarily scan the crystal along the characteristic crystal size. However, if CSD is determined beforehand, CLD can be calculated from the CSD with statistical method [4] .
In this paper, first, when crystal shape was defined from the characteristic crystal size, the matrix of each crystal shape which transforms CSD into CLD in a uniform manner was calculated with Monte Carlo analysis. Secondly, CSD and CLD were actually measured in suspension of acetaminophen (AAP) in ethanol and suspension of L-arginine (Arg) in water to demonstrate the validity of 2 matrices. Lastly, these matrices were multiplied by some simple CSD models to test the properties of these matrices and demonstrate the utility of this transformation.
Because this transformation is simply represented by a matrix, it is easy to apply the matrix to inverse transformation and this method is assumed to contribute significantly to in-line measurement of CSD. In some of previous studies [2] [3] , discretizing was used to solve complex integral problems. In this paper, by using Monte Carlo analysis instead of discretization, the transforming matrix can be calculated quickly and accurately. Translation, which is one of the variables defining chord length, was made to exist within variable range and weighting was performed for each range in many of previous studies [2] [3] . In this paper, translation is made to exist within fixed sufficient range in order to avoid weightings in CLD calculation process. In addition, characteristic crystal size is added to the variables defining chord length, which have been composed of rotation angles around 3 axes and a translation [2] [3] [4] , in order to avoid complex integrals and apply the change in crystal shape with characteristic crystal size to the transforming matrix.
2. Theory
2.1. Principle of Chord Length Measurement with FBRM
Particle Track G400, which can measure CLD in line based on FBRM, was used in this paper. Focused beam from probe enters suspension in vessel, and chord length is measured within a range of 1 to 1000 μm based on detection time of backscattered light when beam runs cylindrically at the speed of 2 m/sec. The concept of FBRM is shown in Figure 1.
In Figure 1, the cylinder along which the beam runs has a large diameter in comparison to crystals within the measuring range, and so the beam path can be regarded as a straight line.
As seen from Figure 1, because the parts of crystals where chord lengths are measured differ from one another, CLD differs from CSD.
2.2. Function Which Determines Chord Length
First, it is considered that crystal shape P is defined only from vertex coordinates and that the vertex coordinates are mapping of characteristic crystal size LCS. At this time, Equation (1) is established.
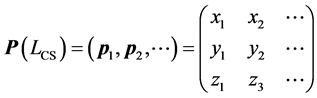 (1)
(1)
where 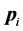 is the ith position vector of vertex coordinate and P is
is the ith position vector of vertex coordinate and P is 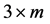 matrix in which m position vectors of vertex coordinates defining crystal shape are placed in m columns.
matrix in which m position vectors of vertex coordinates defining crystal shape are placed in m columns.  Axis is defined as the beam scanning direction, z axis as the beam traveling direction, and y axis as the other direction. Due to calculation, one of the 2 points which are the most distant from each other of all the vertex coordinates is sited at the origin. This model can be used when crystals are regarded as polyhedra. Then, a domain of LCS is represented by Equation (2) in order to adjust LCS to the measuring range of FBRM.
Axis is defined as the beam scanning direction, z axis as the beam traveling direction, and y axis as the other direction. Due to calculation, one of the 2 points which are the most distant from each other of all the vertex coordinates is sited at the origin. This model can be used when crystals are regarded as polyhedra. Then, a domain of LCS is represented by Equation (2) in order to adjust LCS to the measuring range of FBRM.
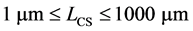 (2)
(2)
Secondly, projection area 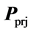 of crystal seen from FBRM probe window is defined from crystal shape P and rotation angles
of crystal seen from FBRM probe window is defined from crystal shape P and rotation angles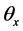 ,
,  , and
, and 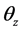 around 3 axes. At this time, Equations (3) and (4) are established.
around 3 axes. At this time, Equations (3) and (4) are established.
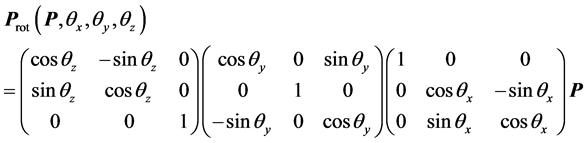 (3)
(3)
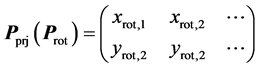 (4)
(4)
where the subscript rot means vertex coordinate after rotation, and projection area 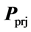 simply discards information on z axis of
simply discards information on z axis of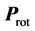 . Then, domains of
. Then, domains of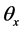 ,
, 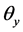 , and
, and 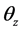 are represented by Equation (5).
are represented by Equation (5).
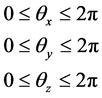 (5)
(5)
Thirdly, because the beam scans crystals along the ![]() plane, translation toward z axis or
plane, translation toward z axis or ![]() axis direction doesn’t change the relationship between projection area and trajectory of the beam. Therefore, projection area
axis direction doesn’t change the relationship between projection area and trajectory of the beam. Therefore, projection area ![]() including information on the distance from trajectory of the beam is defined only from
including information on the distance from trajectory of the beam is defined only from ![]() and translation
and translation ![]() toward
toward ![]() axis. At this time, Equation (6) is established.
axis. At this time, Equation (6) is established.
![]() (6)
(6)
where the subscript transl means vertex coordinate after translation, and ![]() is the matrix which adds
is the matrix which adds ![]() to
to ![]() coordinates of vertex coordinates
coordinates of vertex coordinates ![]() before translation. Then, a domain of
before translation. Then, a domain of ![]() is represented by Equation (7).
is represented by Equation (7).
![]() (7)
(7)
where it is desirable that ![]() is large enough for the largest crystal to be calculated. In this paper,
is large enough for the largest crystal to be calculated. In this paper, ![]() is defined as the distance between 2 points which are the most distant from each other of all the vertex coordinates of the crystal the characteristic crystal size of which is 1000 μm.
is defined as the distance between 2 points which are the most distant from each other of all the vertex coordinates of the crystal the characteristic crystal size of which is 1000 μm.
Lastly, chord length LCL is defined as the length of line intersection of projection area ![]() and an
and an ![]() axis. To calculate LCL in a uniform manner, intersections
axis. To calculate LCL in a uniform manner, intersections ![]() of an
of an ![]() axis and line segments between all combinations of 2 points from m vertex coordinates of
axis and line segments between all combinations of 2 points from m vertex coordinates of ![]() are to be calculated. In the case that the line segment and an
are to be calculated. In the case that the line segment and an ![]() axis correspond and that the line segment and an
axis correspond and that the line segment and an ![]() axis don’t intersect,
axis don’t intersect, ![]() is defined as not a number (NaN). At this time, Equation (8) is established.
is defined as not a number (NaN). At this time, Equation (8) is established.
![]() (8)
(8)
The set of mC2 intersection coordinates ![]() is represented by a vector
is represented by a vector ![]() in Equation (9).
in Equation (9).
![]() (9)
(9)
At this time, the chord length LCL is represented by Equation (10).
![]() (10)
(10)
However, when LCL is smaller than the measuring lower limit or all of the intersection coordinates ![]() are NaN, LCL is defined as 0, and the range of LCL is represented by Equation (11).
are NaN, LCL is defined as 0, and the range of LCL is represented by Equation (11).
![]() (11)
(11)
2.3. Strict Transformation from CSD to CLD with Multiple Integral
A domain of crystal size in the jth fraction when the domain of crystal size in Equation (2) is divided into n equal parts by a logarithmic scale is represented by Equation (12).
![]() (12)
(12)
Similarly, a range of chord length in the ith fraction when the range of chord length in Equation (11) except 0 is divided into n equal parts by a logarithmic scale is represented by Equation (13).
![]() (13)
(13)
Originally, it is not necessarily required that the number of fractions on crystal size is the same to that on chord length. At this time, the probability that one of an infinitely large number of crystals in Equation (12) is measured as the chord length in Equation (13) is to be calculated. First of all, LCS by a logarithmic scale and![]() ,
, ![]() ,
, ![]() , and
, and ![]() by a linear scale are assumed to be distributed uniformly in Equation (12), (5), and (7) respectively. Therefore, joint probability density function f of 5 independent variables satisfies the relationship expressed by Equation (14).
by a linear scale are assumed to be distributed uniformly in Equation (12), (5), and (7) respectively. Therefore, joint probability density function f of 5 independent variables satisfies the relationship expressed by Equation (14).
![]() (14)
(14)
Then, 5 variables are arranged to be denoted by a vector ![]() in Equation (15).
in Equation (15).
![]() (15)
(15)
Moreover, domains of 5 variables in Equations (12), (5), and (7) are arranged to be denoted by![]() , and Equation (16) is established.
, and Equation (16) is established.
![]() (16)
(16)
where the integrated value in all of the domains K is independent of fraction number j because the integrated values in all of the fractions by a logarithmic scale are the same to one another when the domain of crystal size is divided into equal parts by a logarithmic scale. In the domains![]() , the probability
, the probability ![]() that a crystal is measured as the chord length in Equation (13) is represented by Equation (17).
that a crystal is measured as the chord length in Equation (13) is represented by Equation (17).
![]() (17)
(17)
Because chord length is clearly defined from 5 independent variables (see Section 2.2), the integrated value ![]() in the target range is uniquely calculated for each combination of fraction numbers
in the target range is uniquely calculated for each combination of fraction numbers ![]() and
and![]() . In addition,
. In addition, ![]() doesn’t change with
doesn’t change with ![]() when
when ![]() is larger than a certain value (see Section 2.2). In actual vessels,
is larger than a certain value (see Section 2.2). In actual vessels, ![]() is much larger than this value and so the value of
is much larger than this value and so the value of ![]() is the same to the value calculated in Equation (17). Therefore, if Equation (17) is computable, the probability is strictly calculated. This probability is a contribution of the domain of crystal size in the jth fraction to the range of chord length in the ith fraction. Contributions of the domains of crystal size in n fractions are multiplied by the numbers of crystals and summed up to calculate the expected value of the range of chord length in the ith fraction. Therefore, Equation (18) is established.
is the same to the value calculated in Equation (17). Therefore, if Equation (17) is computable, the probability is strictly calculated. This probability is a contribution of the domain of crystal size in the jth fraction to the range of chord length in the ith fraction. Contributions of the domains of crystal size in n fractions are multiplied by the numbers of crystals and summed up to calculate the expected value of the range of chord length in the ith fraction. Therefore, Equation (18) is established.
![]() (18)
(18)
where ![]() is the count of crystals with chord lengths in the ith fraction and
is the count of crystals with chord lengths in the ith fraction and ![]() is the number of crystals with crystal sizes in the jth fraction. Equation (18) can be generalized and by using vectors
is the number of crystals with crystal sizes in the jth fraction. Equation (18) can be generalized and by using vectors ![]() and
and ![]() which adapt vector indices to fraction numbers of CLD and CSD, Equation (19) is established.
which adapt vector indices to fraction numbers of CLD and CSD, Equation (19) is established.
![]() (19)
(19)
For the following discussion, ![]() is called shape transformation matrix.
is called shape transformation matrix.
2.4. Approximate Transformation from CSD to CLD with Monte Carlo Analysis
The integration range of Equation (17) is too complex for the exact solution to be obtained. Therefore, Monte Carlo analysis is performed with uniformly distributed pseudorandom number![]() . First of all,
. First of all, ![]() is uniformly distributed in the range represented by Equation (20).
is uniformly distributed in the range represented by Equation (20).
![]() (20)
(20)
At this time, to make 5 independent variables have the domains in Equations (12), (5), and (7), and to make Equation (14) about probability density established, 5 independent variables are defined as Equations (21), (22), and (23) with random number.
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
However, Equation (22) is established only if the directions of crystals are uniformly distributed regardless of crystal shape and the direction of the suspension flow. 5 random numbers change for each trial and the dependent variable LCL is calculated on each trial. By using the total number of trials KMC instead of sample space K in Equation (17) and the number of times ![]() that the events have happened (i.e. the number of times that crystals have measured as the chord length in Equation (13)) instead of probability event
that the events have happened (i.e. the number of times that crystals have measured as the chord length in Equation (13)) instead of probability event![]() , the probability is calculated likewise in Equation (17) to obtain Equation (24).
, the probability is calculated likewise in Equation (17) to obtain Equation (24).
![]() (24)
(24)
where the subscript MC means the value about Monte Carlo analysis. If r is true random number, the approximate probability ![]() approaches the exact probability
approaches the exact probability ![]() as the total number of trials KMC increases. In this paper, pseudorandom number was created with MATLAB 7.5.0 (R2007b).
as the total number of trials KMC increases. In this paper, pseudorandom number was created with MATLAB 7.5.0 (R2007b).
3. Experiments
3.1. Substances
In this paper, the verification experiment was performed with acetaminophen (CH3CONHC6H4OH, abbreviated to AAP) and L-arginine (C6H14N4O2, abbreviated to Arg). AAP, the molecular weight of which is 151.16, is a white crystalline compound, hardly soluble in water and readily soluble in ethanol. AAP has 3 kinds of polymorphs. AAP is often used as an analgesic antipyretic or a cold medicine. In the verification experiment, ethanol was purchased from Wako Pure Chemical Industries, Ltd. (Osaka, Japan) and AAP from Tokyo Chemical Industry Co., Ltd. (Tokyo, Japan). Then, Arg, the molecular weight of which is 174.02, is a white crystalline basic amino acid, readily soluble in water and hardly soluble in ethanol. Arg has 2 kinds of pseudo polymorphs: anhydrate and dehydrate. Arg also activates immune function and accelerates cell proliferation. In the verification experiment, Arg was purchased from Wako Pure Chemical Industries, Ltd. (Osaka, Japan).
3.2. Experimental Apparatus
Solution temperature and CLD were measured with the apparatus shown in Figure 2.
Solution temperature was measured with platinum electrode (Pt100, JISC1604-1997/IEC 751). CLD was measured with FBRM (made by Mettler-To- ledo, model G400).
Measurement conditions of FBRM are described below.
・ The measuring range is 1 - 1000 μm.
・ The measurement mode is Macro.
・ The measuring range is divided into 30 equal parts by a logarithmic scale.
・ The wavelength of the laser beam is 780 μm.
3.3. Experimental Procedure
3.3.1. Verification Experiment with AAP
AAP (45 g) was added to ethanol (300 mL) to prepare a saturated solution at 20˚C. Then, with the solution held at 20˚C, AAP seed crystals were added to the solution under 5 conditions. The suspension of AAP in ethanol was stirred and the crystals were washed for about 30 min with CLD from FBRM measured. After it was confirmed that CLD was steady, the suspension was sampled at the same time that CLD was recorded and CSD was measured with an optical microscope. The experimental condition is showed in Table 1.
In Table 1, coarse seed means crystals from a reagent bottle and fine seed means crystals crashed with a mortar.
3.3.2. Verification Experiment with Arg
The experiment with suspension of Arg in water was performed likewise in section 3.3.1. The experimental condition is showed in Table 1.
3.3.3. Creation of Shape Transformation Matrix
Shape transformation matrix ![]() on each substance was created with MATLAB 7.5.0 (R2007b). At this time, AAP crystal images (Figure 3) obtained in section 3.3.1 and Arg crystal images (Figure 4) obtained in section 3.3.2 were used as
on each substance was created with MATLAB 7.5.0 (R2007b). At this time, AAP crystal images (Figure 3) obtained in section 3.3.1 and Arg crystal images (Figure 4) obtained in section 3.3.2 were used as
![]()
Figure 3. Sample of AAP crystal image. Saturation was set to −100 with Microsoft Office 2010. Scale bar the length of which was calculated from a micrometer was inserted with Microsoft Paint.
![]()
Figure 4. Sample of Arg image. Saturation was set to −100 and brightness to 100 with Microsoft Office 2010. Scale bar the length of which was calculated from a micrometer was inserted with Microsoft Paint.
reference, and crystal shape ![]() of each crystal was defined as following. The crystal shape of AAP is similar regardless of crystal size and the shape is an octahedron of 3 axes ratio of 1:1:1.5 which intersect at the middle points (Figure 5). The crystal shape of Arg is similar regardless of crystal size and the shape is a rectangular solid of 3 sides ratio of 1:1:3 (Figure 6).
of each crystal was defined as following. The crystal shape of AAP is similar regardless of crystal size and the shape is an octahedron of 3 axes ratio of 1:1:1.5 which intersect at the middle points (Figure 5). The crystal shape of Arg is similar regardless of crystal size and the shape is a rectangular solid of 3 sides ratio of 1:1:3 (Figure 6).
In addition, the characteristic crystal size of each substance was defined as the black line of each model shape in Figure 5 and Figure 6. The total number of trials in Monte Carlo analysis was 25,000,000 and the size of shape transformation matrix was![]() .
.
3.4. Error Evaluation
The absolute value of CLD hardly has quantitative information, because ![]() in an actual system is unknown and a much larger value than was used in probability calculation, and changes with time. However, when
in an actual system is unknown and a much larger value than was used in probability calculation, and changes with time. However, when ![]() is sufficiently large, each relative value of elements contained in
is sufficiently large, each relative value of elements contained in ![]() doesn’t change with
doesn’t change with![]() . Therefore, if CSD after shape transformation is directly proportional to CLD, it can be confirmed that the shape transformation matrix is accurate and that the theory in this paper is valid. In addition, in the case that CSD tries to be measured with FBRM apparatus in practice, CSD cannot be calculated with CLD and
. Therefore, if CSD after shape transformation is directly proportional to CLD, it can be confirmed that the shape transformation matrix is accurate and that the theory in this paper is valid. In addition, in the case that CSD tries to be measured with FBRM apparatus in practice, CSD cannot be calculated with CLD and ![]() immediately from the above reason. At this time, the data needs handling correctly. For example, the concentration is measured secondarily and temporary CSD is multiplied by a constant based on mass balance. In this case, L3-weighted distribution is usually used, and so the shape transformation matrix
immediately from the above reason. At this time, the data needs handling correctly. For example, the concentration is measured secondarily and temporary CSD is multiplied by a constant based on mass balance. In this case, L3-weighted distribution is usually used, and so the shape transformation matrix ![]() is assumed to function the best when the error of L3-weighted distribution is practically small. L3-Weighted distribution
is assumed to function the best when the error of L3-weighted distribution is practically small. L3-Weighted distribution ![]() is calculated from no-weighted distribution N by using Equation (25).
is calculated from no-weighted distribution N by using Equation (25).
![]() (25)
(25)
where L is a diagonal matrix the ith diagonal element of which is the average of the ith fraction ![]() and
and ![]() is the geometric average of both ends
is the geometric average of both ends ![]() and
and ![]() of the ith fraction. For 3 no-weighted distributions: CSD measured with an optical microscope before and after the transformation and CLD from FBRM, L3-weighted distributions were calculated by using Equation (25). Then, every L3-weighted distribution was normalized and the total amount of every L3-weighted distribution was adjusted to 1 to exclude quantitative discussion. Normalized L3-weighted distribution
of the ith fraction. For 3 no-weighted distributions: CSD measured with an optical microscope before and after the transformation and CLD from FBRM, L3-weighted distributions were calculated by using Equation (25). Then, every L3-weighted distribution was normalized and the total amount of every L3-weighted distribution was adjusted to 1 to exclude quantitative discussion. Normalized L3-weighted distribution ![]() is represented by Equation (26).
is represented by Equation (26).
![]() (26)
(26)
At this time, CSD measured with an optical microscope was assumed to be a calculated vector, CLD from FBRM a observed vector, and relative error E was defined as a 2-norm of difference between a calculated vector and observed one. E is represented by Equation (27).
![]() (27)
(27)
E from CSD after the transformation was compared with that before the transformation, and the validity of ![]() was discussed.
was discussed.
3.5. Test of Properties of Matrices with Model CSD
The properties of the shape transformation matrices of AAP and Arg, which were created in section 3.3.3 and the validity of which was demonstrated in section 3.4, were tested by being multiplied by the following 2 CSD models to demonstrate the utility of the transformation. Figure 7 shows the case that crystals exist only in fraction No. 28 and Figure 8 shows the case that every fraction has the same number of crystals. The total amount of every CSD model is adjusted to 1.
4. Results and Discussion
For example, normalized L3-weighted distributions under cond. 3 and cond. 9 are shown in Figure 9 and Figure 10 respectively.
![]()
Figure 9. Normalized L3-weighted distribution under cond. 3.
![]()
Figure 10. Normalized L3-weighted distribution under cond. 9.
In Figure 9 and Figure 10, calc. means values from optical microscopy, obs. values from FBRM, and before and after values before and after the shape transformation respectively. The examples in Figure 9 and Figure 10 show that CSD was transformed to approach CLD in both systems. The results of the error evaluation performed in the manner of section 3.4 are shown in Table 2.
At this time, the rate of change in relative error obtained before and after shape transformation was calculated. In addition, the average of the rate of change by each substance was calculated to demonstrate the validity of the shape transformation matrix on each substance.
Table 2 shows that contrary to expectations the error was increased by the transformation under cond. 7 and cond. 8. This phenomenon was assumed to occur because under these 2 conditions the suspensions contained many fine seed crystals, the aspect ratio of which was smaller than that of model shape defined in Figure 6. Therefore, this result shows that ![]() didn’t function correctly when actual crystal shape differed greatly from defined crystal shape
didn’t function correctly when actual crystal shape differed greatly from defined crystal shape![]() . However, the errors under the other conditions and the average by each substance show that the errors were almost always decreased greatly and that the method in this paper was assumed to be valid.
. However, the errors under the other conditions and the average by each substance show that the errors were almost always decreased greatly and that the method in this paper was assumed to be valid.
Then, CLDs which ![]() on AAP and Arg, the validity of which had been demonstrated, multiplied by 2 CSD models shown in Figure 7 and Figure 8 became are shown in Figures 11-14. The total amount of every CLD was adjusted to 1.
on AAP and Arg, the validity of which had been demonstrated, multiplied by 2 CSD models shown in Figure 7 and Figure 8 became are shown in Figures 11-14. The total amount of every CLD was adjusted to 1.
Figure 11 and Figure 12 show that both of the distributions were assumed to become broad in contrast to the monodispersed system in Figure 7 and that both of the most frequent values came to exist in fraction No. 25 less than the fraction number in which the most frequent value of CSD model 1 had existed by 3. This phenomenon was assumed to show that crystals were rarely measured as the same chord length as the characteristic crystal size and that almost all of the crystals were measured around the edge or at a slant. In addition, crystals
were sometimes measured as a longer chord length than the characteristic crystal size only for Arg. This was because the chord length around the body diagonal line was longer than the characteristic crystal size. The effect that crystals were measured around the edge or at a slant affected CSD complexly, depending on crystal shape. For example, Figure 12 shows that CLD was split in contrast to the monodispersed system in Figure 7. Inversely, CSD doesn’t necessarily show multiple peaks when CLD shows multiple peaks, which is assumed to show that serious errors can occur in the case that CLD is handled as it is as CSD. Moreover, taking the fact that CLD wasn’t split in Figure 11 into account, it is assumed that this effect heavily depends on crystal shape and that the data cannot be transformed in a unified manner for all of the crystal shapes.
Then, Figure 13 and Figure 14 show that the relative number was increased as the chord length became larger within the ranges of small fraction numbers and of middle fraction numbers in contrast to the uniform distribution in Figure 8. This was because the probability that the crystals overlapped with trajectory of the beam was decreased as the crystal size became smaller against the fixed constant yd. However, within the ranges of large fraction numbers, the trend was reversed. This was assumed to occur because of the effect that crystals were measured around the edge or at a slant, which is mentioned above.
Consequently, the state of CSD cannot be discussed from CLD without using shape transformation matrix, and the utility of the shape transformation matrix calculated in this paper was assumed to be demonstrated.
5. Conclusions
By using Monte Carlo analysis, shape transformation matrices which transformed CSD into CLD for the crystal shape defined beforehand were created. The validity of these shape transformation matrices were tested with the suspension of AAP in ethanol and the suspension of Arg in water. The verification experiments show that the relative error between CLD and CSD after transformation was significantly smaller than that between CLD and CSD before transformation only in the case that the actual crystal shapes corresponded with the definition. Therefore, the validity of this transformation method of CSD with the shape transformation matrix was demonstrated. Then, the virtual experiments in which the CLDs were obtained by the shape transformation matrices multiplied by some CSD models show that the trend and the statistics of CSD greatly differed from those of CLD and that the degree of the difference depended on the crystal shape. In other words, the state of CSD cannot be discussed from CLD without using shape transformation matrix, and the utility of the shape transformation matrix calculated in this paper was demonstrated.
In this paper, the crystal shape was assumed to be similar regardless of crystal size for simplicity, but actually, shape transformation matrix can be created even if crystal shape is defined as a mapping of the crystal size. This mapping is accurately researched beforehand and inserted in the shape transformation matrix to enable the matrix to shape-transform for more general cases. In addition, by using the shape transformation matrix with the method in this paper for inverse transformation, the algorithm transforming CLD into CSD is created to realize real-time monitoring of CSD with FBRM. Many of the operations containing matrix can be performed in a very short time with numerical analysis software. In other words, the fact that shape-transforming operator was obtained as matrix in this paper seems to contribute to transforming CLD into CSD with the quality of in-line in FBRM remaining.
Acknowledgements
We express thanks to Mettler-Toledo K.K. BU AutoChem for technical support.
Nomenclature
![]() normalized
normalized![]() [-]
[-]
E domain of![]() [
[![]() ]
]
E relative error [-]
![]() joint probability density function [
joint probability density function [![]() ]
]
K sample space [![]() ]
]
![]() set of LR in diagonal matrix [m]
set of LR in diagonal matrix [m]
LCL chord length [m]
LCS crystal size [m]
LR geometric average of both ends of fraction [m]
![]() number of vertices [-]
number of vertices [-]
M probability event [![]() ]
]
![]() no-weighted distribution [#]
no-weighted distribution [#]
N number of crystals [#]
N number of fractions [-]
![]() position vector of vertex coordinates [m]
position vector of vertex coordinates [m]
![]() set of
set of ![]() in matrix [m]
in matrix [m]
r pseudorandom number [-]
![]() set of 5 independent variables [
set of 5 independent variables [![]() ]
]
![]() shape transformation matrix [-]
shape transformation matrix [-]
X x-coordinate [m]
![]() intersection of
intersection of ![]() -axis and line segment [m]
-axis and line segment [m]
![]() set of
set of ![]() in vector [m]
in vector [m]
Y y-coordinate [m]
yd translation toward y-axis [m]
yd, max required minimax value of yd [m]
z z-coordinate [m]
![]() L3-weighted distribution [# m3]
L3-weighted distribution [# m3]
![]() rotation angle around
rotation angle around ![]() -axis [rad]
-axis [rad]
![]() rotation angle around y-axis [rad]
rotation angle around y-axis [rad]
![]() rotation angle around z-axis [rad]
rotation angle around z-axis [rad]
after after transformation
before before transformation
calc calculated value
CLD chord length distribution
CSD crystal size distribution
MC Monte Carlo analysis
obs observed value
prj projection
rot after rotation
transl after translation
AAP acetaminophen
Arg L-arginine
FBRM focused beam reflectance measurement