Received 10 March 2016; accepted 6 June 2016; published 9 June 2016

1. Introduction
The sanitary sewer overflow (SSO) is a condition in which untreated sewage is discharged from a sanitary sewer into the surroundings before reaching to the treatment facility. The cause of SSOs can be of multiple sources, such as blockage of sewer pipelines, infiltration of storm water into the line during rainfall, pump station failures, and broken or collapsed pipe lines. Therefore, in the sewer pipeline management, the sanitary sewer overflow (SSO) is an important indicator of the system’s performance. Such SSOs are common issues to all municipalities. It is meaningful to study such events to assist decision makers in the facility management.
The arrivals of those events may be assumed to random. Such assumption of independent successive events leads to the Poisson process. In a Poisson process, the inter-arrival times display an exponential distribution [1] . Such memory-less property provides advantages in modeling events in sequence. In civil engineering, this approach has been applied in modeling rainfalls [2] , and accident frequency analysis [3] .
In real life, the homogenous memory-less assumption may not be justified. The prediction may also be conservative [4] . The process can be more accurately modeled with a non-homogenous model. Existing reliability models include Crow’s model [5] and Cox-lewis’ mode [6] , both use the Weibull distribution to fit the “time to failure” data. In this study, in order to explore the arrival of overflows during the dry weather, the Weibull distribution is used to verify the pattern of SSO arrivals. The results will assist stakeholder and decision makers in the management of sewer facilities [7] .
In the sewer system management, research has been conducted in several directions. In general, it can be categorized into three major concentrations. The first concentration is the reliability analysis of the system. This method focuses on the failure data and explores the reliability through the data analysis. Atypical example is the research conducted by Jin and Mukherjee [7] [8] . In this research, the authors focused on the blockages, by using a set of data collected on a sewer system. They proposed methods to explore the arrival patterns deeply. They also proposed a life time trend based on the reliability analysis. Applications are also explored with specific examples demonstrated. Similar research has also been conducted in terms of hydraulic evaluation of systems [9] - [12] ; and situational simulation to support decision making in co-dependent infrastructure systems [13] .
The second category is the condition prediction. The Markov chains model has been applied extensively in this research concentration. For example, Wirahadikusumah et al. discussed several challenging issues in the sewer pipe condition prediction [13] . They presented the Markov chains model, which is the most popular technique in simulating the condition deterioration. However, the condition transition probability estimation is a huge challenge. Jin and Mukherjee further proposed specific methods to estimate the probabilities [14] [15] . They further investigated the sensitivity of Markov chains model, which is a big step in this research category. Other related studies can be found in [16] - [19] .
The third category can be the life cycle analysis of the sewer system. Both life cycle cost and life cycle assessment have been conducted upon the system. For example, Najafi and Kim compared the life cycle cost of the trenchless and conventional open-cut pipeline [20] . They conclude that the trenchless method has its advantages. Lassaux et al. conducted a life cycle assessment of the water from the pump station to the wastewater treatment plant [21] . Detailed inventories are summarized in the study. Jin conducted both the life cycle cost and life cycle assessment of three rigid sewer pipes, namely, non-reinforced concrete pipe (NRCP), reinforced concrete pipe (RCP) and Vitrified clay pipe (VCP) [22] . Detailed costs and environmental impacts are presented in the study. Other related research can be found in [23] - [25] .
This research is similar to the study conducted by Jin and Mukherjee [7] . Instead of focusing on the sewer blockage, this study evaluates the SSO issues under the dry weather condition. In order to investigate the reliability of the sewer system via SSO data, the Weibull distribution is applied upon various sets of SSO data combinations.
2. Methodology
In order to evaluate the arrival pattern of SSO events, the time to arrival data are explored. Considering that the data ranges from 2011 to 2014, the yearly data 2011, 2012, 2013 and 2014 are firstly explored individually. The entire dataset is also explored later. The Weibull distribution is adopted to investigate the sequences.
The Weibull distribution has been used to characterize time series data when the arrival rates are not constant. They can be used to model the infant mortality with decreasing failure rate, wear-out situations with increasing failure rate. When the rate is found to be constant, it reduces to an exponential distribution. Specifically, the standard Weibull distribution has the density function
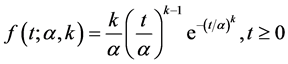 (1)
(1)
and distribution function
 (2)
(2)
where k is the shape parameter, α is the scale parameter. When k = 1, the Weibull distribution becomes an exponential distribution. The arrival rate is constant, therefore, it is a Poisson process. When k > 1, it indicates that the arrival rate increases with time. When k < 1, it means the arrival rate decreases with time.
The 3-parameter Weibull introduces a location parameter location parameter γ. It is used to describe a shift in the distribution. The density function is given by:
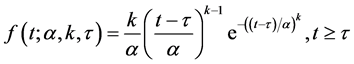 (3)
(3)
and distribution function is
 (4)
(4)
It should be noted that by applying those reliability models, the following assumptions need to be accepted. Firstly, at time zero, all pipes are of equal condition. Secondly, the external impacts are subject to the same condition as well. Strictly, such assumptions can never be applied in real life. However, the application is able to demonstrate meaningful system behaviors [7] .
3. Results and Discussions
Figures 1-5 display results for the individual annual data set. For the 2011data set, the shape parameter is 1.28, indicating the arrival rate increases with time. In terms of 2012 data, the shape parameter is 1.14, the SSOs also arrives in an increased rate over this year. However, the increased trend is gentler than that in 2011. In 2013, the shape parameter drops to 1.1, although it is greater than1, considering it is the life data we are dealing with, the arrival of dry weather SSOs can be reasonably regarded as random. In 2014, the data do not fit the 2-parameters very well. The shape parameter is 2.13, which is not reliable due to the poor fitting. A 3-parameter Weibull fits the data decently as shown in Figure 5. The shape parameter is 1.49. It indicates that dry weather SSOs tends to occur at an increased rate. This can be an evidence that maintenance efforts may not be sufficient during this year.
By considering all available data, both the 2-parameter and 3-parameterWeibull distributions are applied. It can be seen from Figure 6 that the 2-parameter fitting is very poor. The 3-parameter Weibull generates an acceptable good fitting. As shown in Figure 7, the shape parameter is 1.62. Overall, there is an increased arrivalrate of dry weather SSOs during this time period.
Table 1 summarizes the shape parameter for each data set. It can be seen from the table that for the first individual 3 years the shape parameters are relatively close to one. When dealing with the entire data set, the shape
![]()
Figure 1. Weibull fitting for 2011 data.
![]()
Figure 2. Weibull fitting for 2012 data.
![]()
Figure 3. Weibull fitting for 2013 data.
![]()
Figure 4. Weibull fitting for 2014 data.
![]()
Figure 5. 3-Parameter Weibull fitting for 2014 data.
![]()
Figure 7. 3-Parameter Weibull fitting for all data.
![]()
Table 1. Parameters of the analysis results.
parameter jumps to 1.62. One major cause could be the inconsistency of the 2014 data. The 2-parameter Weibull has a poor fitting. Such also indicates that it is important to combine and categorize data into short time interval (such as annual data set), the approach would help to find the causes of abnormal data.
4. Conclusion
The dry weather SSOs can be regarded as an important indicator of the sewer pipeline condition. As a result, the analysis upon such SSO data will assist engineers and managers in the facility management. This paper focuses on the SSOs data that are collected from a municipality. The data are treated as annual data set as well as the entire data set. In terms of analysis results, the shape parameter is able to provide useful information. It shows that in some year, the arrival rate of dry weather SSOs shows relatively constant rate, which is an indication that the general condition of the sewer system stays on the steady condition level. In some other year, an increased SSO arrival rate is noticed. Such findings require attention from the sewer systems manager. There are needs to enhance the system’s performance by investing more maintenance efforts.