Qualitative Properties and Numerical Solution of the Kolmogorov-Fisher Type Biological Population Task with Double Nonlinear Diffusion

Dildora Kabulovna Muhamediyeva^*

National University of Uzbekistan, Tashkent, Uzbekistan.

DOI: 10.4236/jamp.2015.310153                

Abstract

In the present work we study the global solvability of the Kolmogorov-Fisher type biological population task with double nonlinear diffusion and qualitative properties of the solution of the task based on the self-similar analysis. In additional, in this paper we consider the model of two competing population with dual nonlinear cross-diffusion.

Keywords

Double Nonlinearity, Cross-Diffusion, Biological Population, A Parabolic System of Quasilinear Equations, Convective Heat Transfer, Numerical Solution, Iterative Process, Self-Similar Solutions

1. Introduction

Let’s consider in the domain 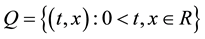parabolic system of two quasilinear equations of reaction-diffusion with double nonlinear diffusion

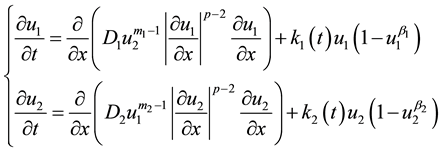(1)

which describes the process of biological populations of the Kolmogorov-Fisher in two-component nonlinear medium, the diffusion coefficient which is equal to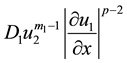, , 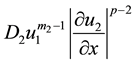where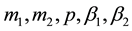

are positive real numbers, and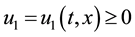, 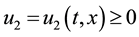are sought solution .

Below we investigate the qualitative properties of the considered problem by constructing self-similar system of equations for (1).

2. Self-Similar System of Equations

Self-similar system of equations we will construct by the method of nonlinear splitting [1] - [3] .

Substitution in (1)

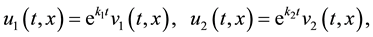
lead (1) to the form:

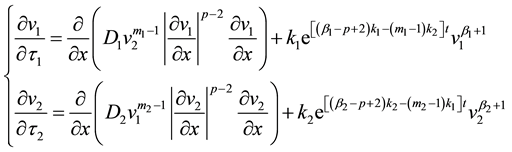(2)

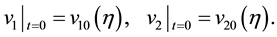
Choosing

,

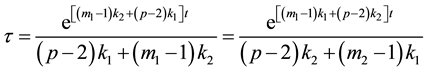we get the following system of equations:

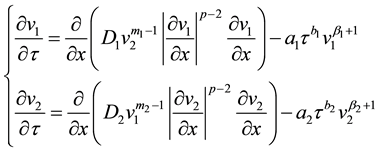(3)

where

,

,

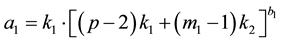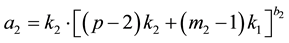For the purpose of obtaining self-similar system for the system of Equation (3) we find first the solution of a system of ordinary differential equations [4] - [7]

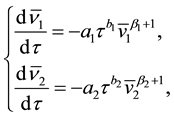
in the form

where

And then the solution of system (3) is sought in the form

(4)

and is selected so

if.

Then for we get the system of equations

(5)

where

(6)

Consider the self-similar solution of system (5) of the form

(7)

Then substituting (7) into (5) with respect to we get the following system of nonlinear degenerate self-similar equations:

(8)

where, Let’s build an upper solutions for system (8).

3. Construction an Upper Solution

If

, , ,

Equation (8) has a local solution of the form

where, ,

Then in the domain Q according to the comparison principle of solutions [1] [8] we get

Theorem 1. Let Then the solution of the task (1) in the domain Q takes place an estimation

where―above-defined functions.

Note that the solution of system (1) when has the following representation in the

.

where―Beta Euler function [9] .

It is proved that this view is self-similar asymptotics of solutions of systems (1).

Thence

.

Carried out computational experiments and numerical results are obtained (see Table 1, Table 2).

4. Conclusion

Thus, it is assumed that the possibility of adequate study of nonlinear equations, biological populations with double nonlinearity based on the method of nonlinear splitting and numerical study of nonlinear processes described by equations with double nonlinearity and analysis of results on the basis of the estimates of the solutions gives a comprehensive picture of the process of multicomponent competing systems of biological populations.

5. Results

Table 1. Numerical results in the case of fast diffusion.

Table 2. Numerical results in the case of slow diffusion.

1) Fast diffusion is shown in Table 1. As an initial approximation it is necessary to take:

, , , , , ,

Parameter values must be Constant a is determined from the condition,:

2) Slow diffusion is shown in Table 2. As an initial approximation it is necessary to take:

, , , , т, ,

Parameter values must be. Constant a is determined from the condition

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Aripov, M. (1988) Method Reference Equations for the Solution of Nonlinear Boundary Value Problems. Fan, Tashkent, 137.
[2]	Belotelov, N.V. and Lobanov, A.I. (1997) Population Model with Nonlinear Diffusion. Mathematic Modeling, 12, 43-56.
[3]	Volterra, V. (1976) The Mathematical Theory of the Struggle for Existence. Science, Moscow, 288.
[4]	Gause, G.F. (1934) About the Processes of Destruction of One Species by Another in the Populations of Ciliates. Zoological Journal, 1, 16-27.
[5]	Aripov, M. and Muhammadiev, J. (1999) Asymptotic Behaviour of Automodel Solutions for One System of Quasilinear Equations of Parabolic Type. France. Buletin Stiintific-Universitatea din Pitesti, Seria Matematica si Informatica, 19-40.
[6]	Aripov, M.M. and Muhamediyeva, D.K. (2013) To the Numerical Modeling of Self-Similar Solutions of Reaction-Diffusion System of the One Task of Biological Population of Kolmogorov-Fisher Type. International Journal of Engineering and Technology, 2, 281-286.
[7]	Aripov, M.M. and Muhamedieva, D.K. (2013) Approaches to the Solution of One Problem of Biological Populations. Issues of Computational and Applied Mathematics, 129, 22-31.
[8]	Murray, D.J. (1983) Nonlinear Diffusion Equations in Biology. Mir, Moscow, 397.
[9]	Huashui, Z. (2010) The Asymptotic Behavior of Solutions for a Class of Doubly Degenerate Nonlinear Parabolic Equations. Journal of Mathematical Analysis and Applications, 370, 1-10. http://dx.doi.org/10.1016/j.jmaa.2010.05.003