1. Introduction
The continuous-time algebraic Riccati equations and their extensions have been investigated extensively in the literature. Recently, the H¥ control problem was solved for linear time-invariant system [1] -[3] and for stoch- astic systems [4] -[7] .
Wu and Luo [8] have commented the iterative solution of the following continuous-time algebraic Riccati equation
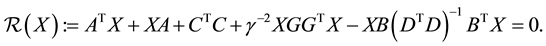(1)
Note that this equation has indefinite quadratic part. Assume there exists a positive semidefinite solution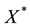 
to (1) with property that real parts of eigenvalues of 
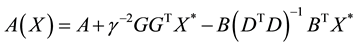are negative. Such type solution is called a stabilizing solution.
The H¥ linear quadratic problems have been introduces by Basar and Bernhard [9] as a two-player zero sum gane. We consider a model for a a two-player zero-sum game, where the control function 
is a minimizing player (or a controller player) of the functional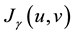 
and the disturbance function 
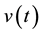is a maximizing player (or a disturbance player), where
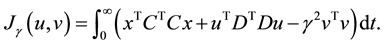
The controller player aims to minimize the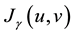 
and the disturbance player aims to maximize the 
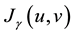under a constrain of the system:
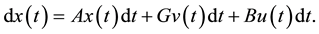(2)
Knowing the stabilizing solution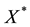 
to (1) we define the following functions:
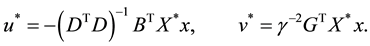
The functions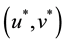 
have the property
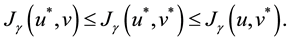
And thus they form the equilibrium point of the two-player zero-sum game described by (2) and the functional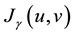
. This fact is well known in the literature and it can be derived using the Pontryagin’s Maximum Principle for example. Moreover, the stabilizing solution is very important solution to Equation (1).
So, why we need to study the iterative equations for computing the stabilizing equation to (1)? Many re- searchers have investigated Riccati Equation (1) and more specially how to compute his stabilizing solution. Lanzon et al. [1] have proposed two effective methods. The first method constructs two matrix sequences where the first sequence converges to the stabilizing solution. The second method avoids the second matrix sequence and defines one matrix sequence which directly approximates the stabilizing solution. Later, Wu and Luo [8] have studied the same equation and the proposed method in [1] . They have commented that the second Lanzon’s method (it is Algorithm 2 [8] ) is not fully effective and by this reason they have introduced the new method described as Algorithm 4 in their paper [8] . Here, we consider an example where these two algorithms will be compared.
Example 1. Let us we take the following matrix coefficients to (1) (using the MATLAB notations):
;
![]()
;![]()
;![]()
;![]()
;![]()
.
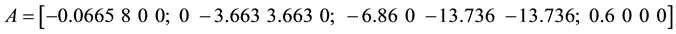We execute Algorithm 2 [8] and Algorithm 4 [8] with the initial point![]()
. Starting Algorithm 2 in MATLAB we obtain the following stabilizing solution to (1) after 4 main iterations and (the average number of iterations for the inner loop is 7):
![]()
And the solution computed by Algorithm 4 is
![]()
Note that the matrix ![]()
is positive definite and ![]()
while the matrix ![]()
is
indefinite and![]()
. In addition![]()
. Thus these two solutions are different! Which of them is sought? We have to check whether the corresponding matrices stabilize system (2).
We compute eigenvalues of ![]()
and![]()
. The eigenvalues of ![]()
have negative real parts
and the matrix ![]()
has one positive eigenvalue. Thus the matrix ![]()
is the stabilizing solution to Equation (1) while the matrix ![]()
is not the stabilizing solution to (1). In addition we have execute the same example with the open software SCILAB (http://www.scilab.org/scilab/about). We apply the SCILAB’s function “lyap” for Algorithm 2 and Algorithm 4. After 4 main iterations Algorithm 2 in SCILAB computes the stabilizing
solution with![]()
. After 18 iterations with Algorithm 4 in SCILAB we obtain the same
solution ![]()
with![]()
. The solution is indefinite and it is not the stabilizing solution.
So, this example gives us the conclusion that the Algorithm 4 described in [8] compute only a solution to (1) and this solution is not always positive definite and this solution is not always stabilizing.
In this reason we confirm that the Lanzon’s method [1] is an effective method for computing the stabilizing solution. His main essential feature is that the iterative process includes two iterative loops-the out loop and the inner loop. We extend the ideas described by Lanzon et al. [1] and Feng and Anderson [6] to propose iterative methods where one matrix sequence is constructed. Here we introduce additional two iterative methods which lead directly to the stabilizing solution. Our contribution is to apply two computational schemes for realization the first iterative equation. Moreover, the second iterative equation is a new method for computing the stabi- lizing solution to (1). We present a few examples for testing the introduced recurrence equations on the MATLAB and SCILAB computational platforms.
We write ![]()
or ![]()
if ![]()
is positive definite or ![]()
is positive semidefinite for any two symmetric matrices X and Y. We use some properties of positive definite and positive semidefinite matrices. A matrix A is said to be asymptotically stable if all the eigenvalues of A lie in the open left half plane.
2. Iterative Methods for Stabilizing Solution to (1)
The first method is the Lanzon’s method [1] and Algorithm 2 from [8] . We present the main theorem with pro-
perties for constructing two matrix sequences of positive semidefinite matrices![]()
. The matrix
sequences are constructed as follows. We take
![]()
(3)
We find ![]()
as the stabilizing solution of the algebraic Riccati equation with definite quadratic part:
![]()
(4)
where
![]()
The matrices ![]()
are stabilizing solutions for the sequence of algebraic Riccati Equations (4). We will prove that the second sequence is monotonically non-decreasing and converges to the unique stabilizing solution to set of Equation (1). We reformulate the convergence theorem introduced in [1] (Theorem 3) and we present it as sufficient conditions to existence the stabilizing solution to (1).
Theorem 1 Assume there exist symmetric matrices ![]()
and ![]()
such that ![]()
and ![]()
and
![]()
, and the pair ![]()
is a stabilizable one. Then for the matrix sequences ![]()
defined by (3), (4) are satisfied for ![]()
1) ![]()
is stabilizable;
2)![]()
;
3) the matrix ![]()
is asymptotically stable for![]()
;
4)![]()
.
Proof. The proof follows the proof of Theorem 3 from [1] .
Theorem 1 presents sufficient conditions for the equation ![]()
has a solution. Such type conditions are introduced here for the considered equation ![]()
for the first time. Theorem 1 confirms the convergence properties of iterative method (3), (4).
Further on, we consider an alternative iteration process where one matrix sequence is constructed. Consider the behaviour of the controller player (u(t)). Assume the controller player knows the matrix![]()
. He wants to
find![]()
. Then he takes![]()
. The system (2) becomes
![]()
And the functional ![]()
is
![]()
The corresponding Riccati equation regarding to ![]()
is
![]()
(5)
where
![]()
Based on recurrence Equation (5) we derive the following new iteration:
![]()
(6)
with![]()
. We perform iteration (6) using two recurrence approaches. The first one is to solve Equation (6) as a Riccati equation. We call this approach “(6) + care”. The second one is to solve Equation (6) applying the Lyapunov iteration:
![]()
(7)
with![]()
. The matrix sequence ![]()
converges to![]()
. Iteration (7) defines the inner loop for iteration (6). We call the second approach “(6) + lyap”. In fact, that is an extension of the Algorithm 2 [8] .
The notation “(6) + care” means that the iteration (6) is solved as a Ricacti equation with unknown matrix![]()
. Each solution![]()
) of (6) is computed as a solution to Riccati Equation (6). The notation “(6) + lyap” stands for the fact that the solution ![]()
to Equation (6) is computed as a limit of the sequence ![]()
and each matrix ![]()
is a solution to iteration (7). Iteration (7) describes the inner loop for finding the matrix sequence
![]()
defined by iteration (6) and it is a Lyapunov iteration for computing![]()
.
Thus, Equation (6) can be considered as a new iteration formula. This equation constructs a new matrix
sequence ![]()
which converges to the stabilizing solution to (1). It is easy to see that the recurrence
Equation (6) is obtained from (4) when we substitute![]()
. This fact is observed by Praveen and Bhasin in Lemma 2 [2] . Thus ![]()
is the stabilizing solution to (7) with![]()
, we conclude
the matrix pair ![]()
is a stabilizable pair and ![]()
is positive de-
finite. This is enough to start iterative process (7) with![]()
. Following Theorem 9.1.1 derived by Lancaster and Rodman [10] it is sufficient to claim iterative process (7) converges.
Further on, we extend the idea for constructing the matrix sequence![]()
. When we put ![]()
in (4) we obtain:
![]()
Next, we extricate the term ![]()
and continue with some matrix
manipulations. We derive
![]()
(8)
We apply the following implementation for the latest recurrence equation:
![]()
(9)
Our thoughts and algebraic manipulations for deriving recurrence Equation (8) show that it is equivalent to the main iterative process (3)-(4). Thus iteration (9) constructs a new matrix sequence which converges to the stabilizing solution of (1). In order to execute iteration (9) we apply the following algorithm:
1) We take![]()
, and ![]()
as a small positive number.
2) We compute ![]()
as a solution to the equation![]()
.
3) For ![]()
we carry out.
a) Compute ![]()
and
![]()
b) Find ![]()
as a solution to the Lyapunov equation![]()
.
c) Algorithm stops when the inequality ![]()
holds.
4) The stabilizing solution is![]()
.
3. Numerical Experiments
We carry out experiments for solving a continuous-time algebraic Riccati equation with an indefinite quadratic
term (1). We construct two matrix sequences ![]()
and ![]()
for each example. The first matrix
sequence is computed using the iterative process (3)-(4). Iteration (4) is a Riccati equation and ![]()
is its stabilizing solution. In addition, we apply two iterations (6) and (9) for computing the stabilizing solution to (1), where one matrix sequence is established. We perform iteration (6) in two ways “(6) + care” and “(6) + lyap”. We are solving Riccati recurrence Equations (4) and (6) with the MATLAB procedure care where the flops are
![]()
per one iteration. The MATLAB procedure lyab is applied for solving (7) and (9) and the flops are ![]()
per one iteration.
Moreover, we have carried out experiments in the open source software SCILAB
http://www.scilab.org/scilab/about. It provides a computing environment for scientific applications. There are functions for solving linear and nonlinear matrix equations. We apply the “ricc” function for solving a con- tinuous Riccati equation and “lyap” function for a linear Lyapunov equation.
Our experiments are executed in MATLAB on a 2.20 GHz Intel (R) Core (TM) i7-4702MQ CPU computer. We use two variables tolR and tol for small positive numbers to control the accuracy of computations. We
denote ![]()
and![]()
. All iterations stop when the inequality ![]()
is satisfied for some![]()
. That is a practical stopping criterion. However, iteration “(6) + lyap” defines two loops- external and inner. The inner loop stops when the inequality ![]()
is satisfied for some integer![]()
.
For our purpose we have executed hundred runs of each value of n for two family of examples. The tables report the maximal number It of iterations for which the inequality ![]()
holds and the average number ![]()
of iterations for all hundred runs of each size. In addition, the variable ![]()
stands for the average number of iterations executed by (7) in order to obtain the stabilizing solution through (6) for all hund- red runs of each size. For instance, the iteration “(6) + lyap” executes ![]()
main iterations and ![]()
for Example 1. The column “CPU” presents the CPU time for execution the corresponding iterations. In our de- finitions the functions randn (p, k) and sprand (q, m, 0.3) return a p-by-k matrix of pseudorandom scalar values and a q-by-m sparse matrix respectively (for more information see the MATLAB description).
Example 2. We consider a family of examples in case![]()
, where the coefficient real matrices are given as follows: ![]()
and C were constructed using the MATLAB notations:
![]()
Results from experiments in Example 2 are given in Table 1 with ![]()
for all values of n.
Example 3. We consider a family of examples in case![]()
, where the coefficient real matrices are given as follows: ![]()
and C were constructed using the MATLAB notations:
![]()
Results from experiments for Example 3 are given in Table 2 with ![]()
for all values of n.
The application of all iterative methods shows that they achieve the same accuracy for different number of iterations. Our conclusions based on experiments are:
1) The execution the iterations (3), (4) and “(6) + care” takes almost the same CPU time (see the corresponding
![]()
Table 1. Example 2. Results from 100 runs for each value of n.
![]()
Table 2. Example 3. Results from 100 runs for each value of n.
columns of the tables). Note that the procedure care in these iterations have to be applied;
2) Iterations based on the solution of Lyapunov equations faster than the iterations based on the solution of Riccati equations;
3) The new iteration (9) is fastest than other iterative methods;
4) Comparing the MATLAB Execution and the SCILAB Execution we note the MATLAB implementations of the considered iterative methods are faster than the same executed in the SCILAB environment. However, the SCILAB implementations achieve the same accuracy and based on the fact it is an open source software we deduce the SCILAB is an useful tool for education to master and PhD students.
The conclusions are indicated by implemented numerical simulations.
4. Conclusion
We have studied two iterative processes for finding the stabilizing solution to generalized Riccati Equations (2). We have made numerical experiments for computing this solution and we have compared the considered methods numerically. We have compared the results from the experiments in regard of number of iterations and CPU time for executing. Our numerical experiments confirm the effectiveness of proposed new method (9). It is introduced here and moreover numerical experiments show its efficiency.
Acknowledgements
The present research paper was supported in a part by the EEA Scholarship Programme BG09 Project Grant D03-91 under the European Economic Area Financial Mechanism.