The Geometrical Foundation of Federigo Enriques’ Gnoseology and Epistemology ()
1. Introduction: Federigo Enriques and His Geometry
Federigo Enriques (1871-1946) was one of the most important European mathematicians lived between the 19th and the 20th centuries. His contributions to mathematical research concerned algebraic geometry. He collabo- rated with Guido Castelnuovo (1865-1952) and Francesco Severi (1879-1961) and contributed to make the Ital- ian school of algebraic geometry one of the most advanced in that period. In Italy, the interest in modern geo- metry dated back to Luigi Cremona (1830-1903). Several great Italian mathematicians developed algebraic geometry in the second half of the 19th century and the results of Castelnuovo, Enriques and Severi on the clas- sification of algebraic surfaces were the ripest fruit of such historical course of research1.
With regard to Enriques’ mathematical background, projective geometry was a quite significant element. The history of projective geometry is long and dates back at least to Girard Desargues (1591-1661)2. However, start- ing from the end of the 18th century-beginning of the 19th century, thanks to the works of Monge, Poncelet and Gergonne, this discipline had an explosive development3. In the 30s of the 19th century, as a consequence of the results obtained by Möbius, Steiner and Plücker―in addition to those of the already mentioned French mathe- maticians―the corpus of theorems connoting projective geometry can be considered complete. However, these results had been obtained by resorting to the cross-ratio, which is a projective invariant, but is based on metrical notions as length of a segment and calculus of the sinus of an angle. This picture changed completely when Christian von Staudt (1798-1867) wrote his Geometrie der Lage (see Staudt, 1847), where projective geometry is founded on purely graphic and synthetic notions. With this work, the critical phase of projective geometry be- gins, the one in which the research deals with the foundations of a discipline and on the nature of its axioms, methods and procedures. As a consequence of:
1) A clarification and extension of the duality law beyond its use in ordinary projective geometry;
2) The invention of the theory of transformation groups and its application to geometry (Lie, Klein);
3) The specification of the nature of the continuum (Dedekind);
4) The critical examination of the axioms of geometry (starting with Pasch), around the 80s of the 19th century abstract geometry was born.
In the period 1890-1900, as a young scholar and, and starting from 1894, as a professor (from 1896 full pro- fessor) of geometria projettiva e descrittiva at Bologna University, Enriques provided fundamental works on projective and abstract geometry. In particular: 1) sui fondamenti della geometria projettiva (see Enriques, 1894 ); 2) Conferenze di geometria: fondamenti di una geometria iperspaziale (see Enriques, 1894-95 ); 3) Lezioni di geometria projettiva (1894, lithography; first published edition, 1898. See Enriques, 1898, 1904, 1996 ). As we will see, all these contributions were far from being merely didactical supports for the students or for whom participated to the conferences: they expressed a clear and specific conception of geometry. Certainly, this conception was based on Enriques’ mathematical knowledge. But not only: already in Conferenze di geo- metria, he begins to deal with a series of gnoseological problem: what are the relations between our perceptive space and the geometrical space? What is the role of mind in the construction of geometry? Does history of ma- thematics play a role in the relations between perceptive and geometrical space and in the way in which our mind constructs concepts and theories or are these relations and the constructive mechanism of our mind given once and forever?
It is known that Enriques was interested in philosophy―scientific philosophy: positivism, Darwinism, expe- rimental psychology―from the period in which he was a student of mathematics at the Scuola Normale in Pisa4. Therefore, he connected his mathematical education and convictions with his epistemological and philosophical
interests, reaching to present a theory of knowledge whose basis is represented by the way in which he inter- preted geometry. The first paper Enriques published on this subject is Sulla spiegazione psicologica dei postulati
della geometria (see Enriques, 1901, 1958 ), but the very masterpiece is the ponderous volume Problemi della scienza (see Enriques, 1906, 1925 ), where his gnoseology and his ideas on the development and nature of science are expounded in details5. Enriques became hence one of the most illustrious representatives of the cos- mopolite milieu which connoted the scientific European culture between the end of the 19th century and the first world war6. To this milieu, mathematicians and physicians―only to mention then most famous ones - as Mach, Poincaré, Hilbert and Painlevé (in the final stage Einstein, too) belonged. Many other philosophers and scientists (not only mathematicians or physicians) belonged, too. Among the Italian mathematicians Giuseppe Veronese, Vito Volterra, Guido Castelnuovo, Corrado Segre, Cesare Burali Forti and Beppo Levi (others could be men- tioned) were part of this environment. However, the role of Enriques is particularly significant because his con- siderations on the nature of geometry, on the relations between geometry and gnoseology, on the nature of science, on the role of history of mathematics and science inside science and mathematics education, on the his- torical interpretations of some authors (in particular his peculiar interpretations of Parmenides’, Zeno’s and De- mocritus’ though and his ideas on Kant’s theory of knowledge7) allow us to consider Enriques’ thought as a complex and interrelated theory, whose core is his conception of geometry, but whose results and ideas go beyond mathematics. Obviously this is true for Poincaré and afterwards for Einstein and for many of the inven- tors of quantum mechanics, too, but we think that Enriques reached, in this field, profound and original ideas and results, which―maybe―can be compared only with Mach’s. For, Enriques extended his engagement to mathematics education, too. If the already mentioned Lezioni di geometria projettiva are a sort of scientific ma- nifesto concerning projective geometry8, Enriques since 1900 began an intense publication of didactical works. Basically, these contributions can be divided into three categories:
1) Texts which can be used as a didactical support at the high schools or in the initial years of the scientific faculties: the masterpiece inside this kind of literature is Questioni riguardanti la geometria elementare (Enri- ques (Editor, 1900)), published in 1900. Enriques is the editor of this text which contains a series of papers of various authors (both professors at the university and teachers in the high schools) where all the topics dealt with are presented so to highlight the role of history of mathematics as a fundamental support for mathematics educa- tion. After the first edition, the content of the Questioni was made wider and not limited to geometry. From the second edition (there are three editions) the work was hence called Questioni riguardanti le matematiche ele- mentari and the third edition, published between 1924 and 1927 is the most complete, a fundamental work in its field. Enriques also edited an edition of Euclid’s Elements.
2) Handbooks for the high schools. In general, these books were written with the collaboration of Ugo Amaldi. The Elementi di geometria (first edition 1903, see Enriques & Amaldi, 1903 ) is a milestone for this kind of treatises, as it is a precipitate in which Enriques’ personal views and a long debate on the best way to present Euclidean geometry converge in an admirable picture;
3) Contributions to theory of education. Insegnamento dinamico9 ( Enriques, 1921, 2003 ) is the most important of them.
What characterized Enriques’ production is its strong internal connection: while dealing with mathematics education, with history of science and mathematics and with gnoseology and epistemology, Enriques took into account the whole of his view. These subjects were not separated, but belonged to a coherent approach.
In this paper, we are going to show that his approach was based on the way in which Enriques conceived geometry (in particular projective and abstract geometry) and its genesis. Just after previous introduction, it contains the following sections:
1) Projective and abstract geometry: their nature and their psycho-physiological genesis;
2) History of science, birth of philosophy, gnoseology: a strict link;
3) Concluding Remarks.
To understand the relations between geometry and gnoseology in Enriques, there are three main themes, which have to be clarified: 1) the role of intuition in abstract geometry; 2) The geometrical space in its connections with rational mechanics and with space in physics; 3) the genesis of geometrical space. The explanation of these three items highlights Enriques’ conception of geometry and its pivotal function inside his theory of knowledge.
2.1. The Role of Intuition in Abstract Geometry
To catch the role ascribed by Enriques to intuition in geometry, it is necessary to examine the way in which he presented the foundations of geometry, in particular as to abstract and projective geometry. The two fun- damental reference points are Conferenze di geometria: fondamenti di una geometria iperspaziale and Lezioni di geometria projettiva. In these works Enriques does not expound personal mathematical researches, but the way in which the subjects are proposed are paradigmatic of his way to conceive geometry and the role played by the intuition inside this discipline. As Vesentini underlines10, according to Enriques, a mathematical theory is con- structed relying upon examples. Therefore, we think the best way to understand the role ascribed by Enriques to the intuition in geometry is to start with an example.
The Conferenze di geometria face several questions concerning the foundation of geometry. Nevertheless, they are developed around a conceptual core: the duality law. Given for granted the duality law in plane and spatial projective geometry, Enriques shows that the law can be extended to other geometrical situations. This process creates different geometrical universes according to some initial axioms and properties which connote these universes and to the words, which are mutually replaced by duality. Obviously, Enriques is aware that the duality law cannot be extended without having proved that the transcription between the two geometrical un- iverses is, in fact, possible, namely that no contradiction arises. Enriques also shows the analytical procedures by which it is possible to transcribe the properties of a universe into the properties of another one. But his very pas- sion and interest is to show and to discuss the geometrical models which arise from different applications of the duality law. The universes which are generated in this manner are abstract because they are, in general, not re- lated to our physical world. Notwithstanding, in Enriques’ view they are treated as potentially physical worlds which can be studied from a mathematical point of view, but which can also be caught by means of a particular and refined kind/kinds of intuition. As alredy said, to make Enriques’ conception clear, we offer an example drawn from the Conferenze.
Our example concerns the geometry of the circles in the plane ( Enriques, 1894-1895: pp. 12-21 ): Enriques considers all the circles of the plane divided in sheaves. Two circles belong to the same sheaf if they have the same radical axis. The polars of a point A to the circles of a sheaf k belong to a sheaf of straight lines. If every point A of the plane is associated to one polar of the sheaf, a polarity is defined such that the polar of each point A belongs to the sheaf of the polars of A with respect to the circles belonging to k. In this polarity each pair of conjugate diameters is orthogonal. If the polarity has a fundamental conic, the conic is a circle of k. Otherwise the polarity itself defines an imaginary circle of k. In this way, k is extended according to the analytical defini- tion of sheaf. If a sheaf has two limit-points, these points are included in the sheaf. The straight lines can belong to k as circles with a radius of infinite length. If three circles, considered two by two, do not belong to the same sheaf, they give rise to three radical axes which mutually saw in a point having the same power with respect to the three circles. This point is called radical centre. All the circles having the same power with respect to a radi- cal centre belong to the same net of circles.
Given these conventions, the geometry of the circles in a plane is based upon three entities: 1) circles; 2) sheaves of circles; 3) nets of circles. The geometrical system created in this manner can be considered a projec- tive space in which the following duality holds in respect to the ordinary projective space:
![]()
Enriques underlines that in the projective abstract geometry of the circles, the points and the straight lines cannot be, in general, distinguished by the circles as, in this context, they share the same graphic properties (Ivi, p. 14). While, if we are going to obtain a distinction between the points (considered as limit-points of a sheaf of circles) and the circles, it is necessary to consider particular surfaces inside the projective space. Specifically, since the determination of the limit-points depends, in each sheaf of circles, upon an equation of second degree, the limit points will correspond to a quadric of the intuitive projective space S. By means of a homography this quadric can be transformed into a sphere, which provides a quite interesting model of the geometry of the circles. Before dealing with some properties of such a model, it is necessary to point out Enriques stressed that, with the consideration of the sphere, we have passed from the pure graphic projective geometry to the metric projective geometry because, obviously, from a graphical point of view, the sphere cannot be distinguished by the other quadrics.
Thus, let us assume that each point of a sphere F of S is a limit-point of a sheaf of circles and let us project stereographically F on the plane π from a point O of F which is in the diameter perpendicular to π. It is possible to associate each point A of S to the circle of π, which is the projection on π of the circle sawed on F by the polar-plane α of A and vice versa. In this way, the circle whose radius is null (points of π) correspond to the points of F and the correspondence is biunivocal without exceptions. The points of S which are external to F correspond hence to real circles of π, the internal point to imaginary circles. Enriques shows that some properties can be deduced by this correspondence. For example: since a plane β of S saws F in a real or imaginary circle, the geometrical place of the limit points of a net of circles is a circle. For: 1) the plane β corresponds by duality to the net of circles; 2) β saws F (which corresponds to the points of π, considered as limit-points) in a circle; 3) the stereographic projection of a circle is a circle. It is necessary to remind the reader this is a metric-projective property, not a merely graphic one, because―as said above―from a graphic point of view, there is no distinc- tion between points and circles in π.
Therefore, if a real circle C of π is considered as an element of the system of circles, then a point A external to F corresponds to the C; but if C is considered as place of the limit points, then a circle of F lying in a plane α corresponds to C. The point A and the plane α are associated in a polarity whose fundamental quadric is F.
Other interesting properties of the system of circles can be deduced, but we do not have room here to deal with them. These properties―Enriques underlines (ivi, p. 16)―are derived from the consideration of the ordi- nary projective geometry and the geometry of the circles as two different interpretations and models of the ab- stract projective geometry.
The stereographic projection plays an important role in this context. Exactly exploiting the isogonality of this projection it is possible to study some properties of the systems of real circles, in particular as to the angles of two circles to which the angle formed by two planes sawing F corresponds. This order of ideas can be continued until proving that the metric geometry of the real circles on the plane and the geometry of a spherical body―to which it corresponds by duality―can be considered as different interpretations (models) of the abstract hyper- bolic geometry.
In all the other subjects connected to abstract geometry and expounded in the Conferenze, Enriques pays a great attention in presenting different models based on different applications of the duality law. He is interested in allowing the reader to get a synthetic view of the geometrical universes he is constructing and explaining ra- ther than to provide analytical details. There are some subjects in which an analytical approach is unavoidable (for example: the problems connected to the metric of a multidimensional variety, ivi, pp. 42-45; to the geodetics in a variety, ivi, pp. 45-50 and to the angle between two lines in a variety, ivi, pp. 50-54), but, if possible, Enri- ques prefers an approach based on a synthetic modelling, as he did for the geometry of the circles in the plane. He followed a similar approach with regard to the involutions of third order in a straight line (ivi, pp. 21-23), to the presentation of the hyperspaces (ivi, pp. 30), to the introduction of the multidimensional varieties (ivi, pp. 34-42), to the historical notes on the determination of the metrical-projective properties, where the concept of Absolute plays a fundamental role (ivi, pp. 60-68), to the presentation of hyperspatial geometry’s axioms (ivi, pp. 68-76), and to the problems concerning the use of the groups of transformations in geometry (ivi, pp. 85-105).
Enriques’ care in presenting the models of the geometries he was speaking about depends in part on the par- ticular historical phase in which he wrote the Conferenze. For, it is well known that the second half of the 19th century was the epoch of the geometrical models (it is enough to think of the Euclidean models of the non- Euclidean geometries). Nevertheless, this approach also indicates a conviction by Enriques: the geometrical models expounded in a synthetic manner are necessary to catch an intuitive view of the geometrical universe one is dealing with. They allow to see such a universe as a whole with its specific objects and properties. The duality law―for some properties―is, from an epistemological point of view a means, a linguistic and conceptual key to see the structural identity among worlds with different objects and from a mathematical point of view a useful instrument to extend a theorem proved for a geometrical universe to other universes. Therefore both the models and the duality law are a part of the geometrical intuition. But what kind of intuition is the one which allows us to see―as in the mentioned example―a point or a straight line as a circle? Certainly it is something different from what we could call the three basic geometrical intuitions: 1) metrical; 2) graphical; 3) connected to the continuity. As we will see, these intuitions are immediately connected by Enriques to our perceptive faculties: However the intuition used in abstract geometry is something different. Enriques explains that:
“The importance of abstract geometry should not be opposed the importance ascribed to the intuition. Ra- ther it consists in the fact that abstract Geometry can be interpreted in infinite ways as a concrete (intuitive) geometry by establishing the nature of its elements: in this manner Geometry, in its development, can bene- fit from infinite different forms of intuition” ( Enriques, 1994-1995: p. 7 . Italics in the Italian text by Enri- ques. All translations of Enriques’ works from Italian into English are ours).
The following words of Per la storia della logica are paradigmantic of Enriques’ conception and they allow us to clarify his ideas on the kind of intuition which operates in abstract geometry:
“The direct comparison of two orders of geometrical properties, or of two geometries, unified in an analyt- ical representation represents a further development because it invites us to reciprocally translate different forms of intuition.” ( Enriques, 1922a: p. 139 . Italics in the Italian text).
After some lines, we read:
“With Klein and Lie abstract geometry reached a great development. With Segre it became an ordinary in- strument in the hands of the contemporary Italian geometers. For nothing is more fertile than the empo- werment of our intuitive power given by this principle (the duality). It almost seems that thousand of spiri- tual eyes are added to the mortal eyes by which it is possible to examine a figure under a certain respect. In this way we can complete many different transfigurations of the figure. While the unity of the object [the geometrical universe] shines in front of the reason which has been enriched in this way” (Ivi, pp. 139-149).
And again:
“Abstract geometry is hence based upon a repetition of the logical analysis of the deductive theories, as far as different systems of concepts and forms of intuitions are concerned” (Ivi, p. 140).
Although these quotation might appear vague, we think they can be interpreted in a precise manner. First of all, let us distinguish―as already underlined―between primary and secondary or superior intuition. When deal- ing with abstract geometry, the reference is to superior intuition. In the third one of our four quotations, Enriques stresses that the force of this intuition has been empowered by abstract geometry. This means that the superior intuition is not something static. Certainly it is a faculty of our mind, but it is not given once and forever. The particular itinerary of geometry―culminated with abstract geometry―got the effect to develop the superior in- tuition, which is hence a historical outcome of the progresses of geometry.
In its turn such intuition was beneficial for the development of abstract geometry itself because the geometers had acquired the habit to think of possible models for different geometrical universes. This can favour the re- search, because if a geometer is able to imagine a global model for some properties, the precise mathematical research can get a conspicuous advantage from this intuitive view, which, obviously, afterwards has to be speci- fied in precise mathematical terms. Hence the superior intuition (or intuitions as Enriques writes, as referring to different geometrical universes) creates something like a prolepsis, an anticipation of the properties which will be studied in details. Therefore, this is the first sense in which geometry is at the basis of the development of our cognitive faculties.
This entire order of problems is also connected to the concept of model. A geometrical model is based―in an initial phase―on the intuition. It is an important support for the research, but it can also be the result of a re- search in which a new and not-well known geometrical universe is interpreted (in this the duality plays a fun- damental role) in the light of the structures of a well known universe. In a slightly different context, Enriques wrote:
“To prove the possibility of an abstract concept, it is enough to show it receives a concrete interpretation” ( Enriques, 1924-1927a, 1983 ; Parte prima, Tomo primo, p. 290. Italics in the original Italian text).
This means exactly to reconduct the structural properties of an abstract and new universe to a better known one.
To summarize: the superior intuition is the faculty of our mind to imagine abstract geometrical universes with their structural laws. This intuition has been developed thanks to the history of abstract geometry. In its turn it is helpful for advanced researches in geometry. The structures of our mind―at least at a superior level―are not given once and forever, but depends on the history of science―in particular of geometry. The intuition is helpful to create models.
2.2. The Geometrical Space in Its Connections With Mechanics and with Space in Physics
Enriques underlined more than once the profound connections between geometrical and physical space. Proble- mi della scienza are emblematic to understand Enriques’ ideas: if one considers geometry as a merely logical doctrine, its connections with physics are scarce. Enriques refuses to accept this one as the only possible ap- proach to geometry: it is a mistake to consider geometry exclusively as a given science in its logical perfection. To understand the nature of the geometrical space, it is necessary to take into account the genesis and the evolu- tion of geometry. The classical way to present the relation between geometry and physics, in which geometry provides the abstract properties of the space, while mechanics operates in a concrete space with the addition of concepts as mass and force is the inheritance of the Kantian conception, in which: 1) science is interpreted as a necessary a priori consequence of our mental structures, given once and forever; 2) the historical genesis and development of geometry and science is not taken into account. In the entire production by Enriques the inade- quacy of an approach based on the consideration of science as a given doctrinal corpus, rather than a living or- ganism, is often pointed out. In particular, if one accepts the evolutionist approach to science, it is not possible to establish a hierarchy among sciences. Each one has its development. Geometry deals with simpler notions, but this does not mean that the genesis of its basic concepts is different from the genesis of the basic concepts used in physics, and in particular in mechanics11. Thence, Enriques explicitly claims that geometry is a part of physics ( Enriques, 1906, 1925: pp. 157-158 ). The first extension of geometry is mechanics, where time, forces, masses are introduced, entities which do not belong to geometry. Since mechanics is an extension of geometry, this means that the two doctrine share―at least―a common origin.
The literature has rightly pointed out this conception of Enriques, in which geometry and physics are two “sister” sciences12.
In La teoria della conoscenza scientifica da Kant ai giorni nostril ( Enriques, 1938, 1983 ), Enriques offers further specifications as to the link between these two sciences. He writes that geometry can be separated from physics by an abstraction. His words are:
“Geometry can be separated from physics only by abstraction. It is necessary to resolve the abstract con- ception in a concrete view of a geometry, which is unified with physics and which is prolonged in this dis- cipline” (Ivi, p. 55).
On the other hand, it seems strange that a mathematician as Enriques, profoundly interested in abstract geo- metry, had highlighted the similarities between geometry and physics without underlying their differences. In fact, this is not the case. At the beginning of the Conferenze di geometria, Enriques stresses the difference be- tween geometry and physics. For, we read:
“The existence of an order concerning the external objects, namely a real space, whose real properties are explained by the axioms as well as the correspondence between this real space and the intuitive space of our sensibility are questions connected to knowledge, but they transcend the field of abstract Geometry. The development of this geometry is independent of such problems. […] From this question neither any- thing, which could destroy the logical value of Geometry, nor anything, which modifies our intuitive con- ception of space can derive. Therefore, not only the possibility, but the mathematical importance of Geo- metry itself are independent of such questions” ( Enriques, 1894-95: p. 3 ).
Is there a contradiction between this view and the ideas expressed in the previous quotations? The answer is that there is no contradiction. First of all, it is necessary to remember that, although La teoria della conoscenza scientifica da Kant ai giorni nostri is a late work by Enriques, while the Conferenze are an early works, Enriques did not change his mind as to the relations between geometry and physics.
His conception can be interpreted like this:
1) The basic concept of geometry and physics has their origin in our intuition. In particular this is true for the concept of space. A perceptive space (as we will see in the next section 2.3.) exists which is common both to geometry and physics. This space can be called the basic perceptive-intuitive space. It is neither the geometrical nor the physical space, but the common basis for both of them. Because of this, geometry and physics (and in particular mechanics) have the same origin in our basic perceptive structure. This is the reason why geometry can be considered a part of physics.
2) Given this common origin, geometry and mechanics have a different development: geometry becomes an abstract discipline. Euclidean geometry is already a highly formalised branch of mathematics, in which the points have no extension, the straight lines have a length but not a width, the plane surfaces have a length, a width, but not a thickness, and so on. By other words: the objects of the Euclidean geometry are not physical objects. While, the development of mechanics is based on experience and experiments and its level of abstrac- tion is different from geometry’s.
3) The further phase of geometry begins with the non-Euclidean geometries and with the projective geometry and gets its highest point with the abstract geometry, based on a set of axioms, which define implicitly the ob- jects to which they are referred. In this phase, and in particular between the end of the 19th century and the be- ginning of the 20th century, the relation between geometry and physics are reconceptualised because: a) the fact that the physical space is Euclidean cannot be given for granted; b) there are some interpretations of abstract geometry, which can be exploited in physics.
We will deal with the problems of item 1) in the next section.
With regard to the item 2), Enriques pointed out the abstract character of geometry starting from the period of Parmenides and Zeno (see section 3. of this paper), or better: Parmenides and Zeno understood this character, which differentiates geometry from physics. We will see that, according to Enriques, the Pythagoreans did not fully catch this difference.
Quite interesting is what Enriques writes as to the development of mechanics: he is convinced―as told―that the intuition is the common basis of the fundamental concepts both of geometry and of mechanics. Therefore, one of Ernst Mach’s―author who is one of the most important reference points of Enriques and with whom he shares many ideas―conceptions on which Enriques does not agree is that the basic concepts of mechanics are provided by the experience. In two magnificent pages of Problemi della scienza ( Enriques, 1906, 1925: pp. 215-216 ) he clarifies his thought: with regard to the birth of the basic concepts of mechanics, the unconscious elaboration of the sensible data represents a more numerous quantity of phenomena and of relations between phenomena than experience. Therefore:
“[…] the intuitive knowledge has a superior probable value than that offered by the knowledge based on experience, as far as both of them are referred to the same relations among phenomena. While, when the precise delimitation of mechanics is necessary as well as the progressive extension of its applicability, the experience is superior to the intuition” ( Enriques, 1906, 1925: p. 216 ).
Therefore, according to Enriques, statics and kinematics are based upon evident principles, which are asso- ciated to the concepts of space and time, from which they directly draw their evidence. In contrast to this, while dealing with dynamics, it is necessary to add new hypotheses drawn from experience because the field of dy- namics is wider and the intuition is not sufficient anymore. Therefore, if one might summarize the situation with a proportion:
Development of geometry: abstraction = development of mechanics : hypotheses introduced by experience
With regard to the item 3), an interesting observation is that, according to Enriques, the space in geometry de- rives from an intuition, but it is not an intuition, it is a concept ( Enriques, 1906, 1925: p. 161 ). One of Kant’s mistakes consists in the fact that he did not distinguish between the space as intuition and the space as concept. The space of abstract geometry is a concept, although it is based upon and, in its turn, it can develop our intui- tion of second order. For this aspect, Enriques fully agreed with the whole movement of ideas known as formal- ism, which reached probably its more mature expression with Hilbert’s Grundlagen der Geometrie13. Therefore Enriques writes that the concept of space can be freely generalised to abstract spaces and that “the theory of ab- stract spaces is an essential part of the geometrical edifice constructed in the last century” ( Enriques, 1906, 1925: p. 162 ). On the other hand, the way in which Enriques presents his considerations as well as his style are always profoundly different from the style of the formalists, which subtends a view that, although sharing important common standpoint with that of the formalists, is based upon different convictions and ways of conceiving the scientific activity. In Problemi della scienza, Enriques expounds the fundamental geometrical properties of the non-Euclidean geometries, but he also reports the famous anecdote on Gauss, according to which Gauss tried to measure the angles of the triangle Brocken-Hohenhagen-Inselberg in order to catch if our space is Euclidean (Ivi, p. 167). This means that, beyond the abstract character of hyperbolic geometry, Enriques was interested in un- derstanding whether our physical universe is Euclidean or hyperbolic. As a confirmation of the fact that Enri- ques, while dealing with abstract geometry, was also interested in its application to mechanics, it is worth re- membering that in the Conferenze, a whole section ( Enriques, 1894-1895: pp. 56-60 ) is dedicated to a mechani- cal interpretation of the metric geometry of the multidimensional varieties. Furthermore, the superior intuition characterizing abstract geometry can be useful in physics, too. Enriques writes what follows with regard to the possibility to get an intuition of the non-euclidean geometries:
“It is true that, despite the construction of an adequate system of concepts, we are in the psychological im- possibility to represent the real phenomena in a picture, which is different from the space of our ordinary intuition. But this sense of necessity, which is joined to our imaginative vision of the space, can say nothing as to the structure of the space itself. The physical reality has no duty to satisfy our representations” (Enri- ques, 1906, 1925, p. 171).
Clear: the ordinary intuition (“intuizione ordinaria”) is not useful to grasp the properties of the non-Euclidean geometry, but the intuition of second level is! Thence, this kind of intuition is not relegated to mathematics, it is also useful to construct some physical models.
To summarize: a system of basic intuitions represents our perceptive key to geometrical and physical space. These spaces are hence born from a common root. The development of geometry and physics has brought to the separations of physical and geometrical space, but they share a fundamental aspect, which is a recall to the intui- tion: the modelization. We have seen that the models, which can represent abstract spaces, play―according to Enriques―a prominent role to make abstract geometry intelligible to the superior intuition. On the other hand, the models are important to describe a physical situation, these models are the more useful the more a physical situation is complex. The models in physics are also a means to represents a phenomenal situation to our mind. They are useful to get an intuitive view on certain sets of phenomena. They are a mean to represent the reality, or part of the reality, as something intelligible. The models are fundamental to develop our intellectual eyes both in geometry and in physics: this is Enriques’ opinion, which clearly transpires from the plurality of models he discussed, in the Conferenze as to abstract geometry, and in Problemi della scienza as to physics, until identify- ing a tradition of physical models which can be defined visual and a tradition which can be defined muscular ( Enriques, 1906, 1925: pp. 269-318 ). But this distinction is connected with the intuition of first level, too, not only with the superior intuition. Therefore, it is now necessary to deal with the initial genesis of the geometrical and of the physical space.
In these two sections we have tried to explain the nature and the role of the intuition of second order in ab- stract geometry and the relations between geometrical and physical space14 in Enriques.
2.3. The Genesis of Geometrical Space
To explain the origin of the geometrical space, Enriques thinks it is necessary to examine the physiological space, which depends on the structure of our senses. According to Enriques three physiological spaces exist: 1) the muscular space as far as it is provided by a specific organ: typically the hands; 2) the visual space; 3) the general muscular space, whose origin is not in a single organ, but in the set of sensations, which can be recon- ducted to the touch. We could call it tactile space.
Enriques is convinced that the mathematical concept of space derives from the spatial representations drawn by the senses from the external world ( Enriques, 1901, 1958: p. 74 ). There is a direct connection between the physiological space and the geometrical one. Precisely: the metric geometry is originated by the specific muscu- lar space; the projective geometry by the visual space and the analysis situs by the general tactile space. The most interesting contributions by Enriques concern the relation between metric and projective geometry. He reasons like this, starting from the visual space: a) the formation of the imagine on the retina is equivalent to a central projection of the object; b) after e series of adaptations―relying upon the movements of the eyes, that is on a muscular action―the binocular vision is a bicentral projection from two centres on two planes ( Enriques, 1901, 1925: pp. 180-181 ). Given a spatial reference frame with a metric, two projections are sufficient to recon- struct the metrical properties of the object. Without such a reference frame, five projections are sufficient. Given this mathematical premise, Enriques points out (Ivi, p. 182) that these conditions, which are necessary and suffi- cient to determine the form and the dimension of an object can be obtained by moving the eyes or by changing the point of observation. But in this manner, muscular actions are involved, too, not only visual properties of the eyes. In other words: if the observer is at rest and his eyes are at rest, too, it is impossible for him to get an idea of the form and dimensions of an object. This is equivalent to claim that the sight functions in a merely projec- tive manner and that, hence, we can get the graphic properties of the object by the observation, but not the me- trical ones. Is this the situation, or are there some mechanisms of the sight which elude this analysis? Enriques thinks to find the answer to this question in some experimental results of Helmholtz’s school (Ivi, p. 182): these experiments proved that the subjects under experiment made several mistakes in the estimations of the distances among objects and of the parallelism between two lines, if they were obliged to use only one eye without mov- ing it. According to Enriques, this implies that there is a perfect correspondence between the physiological as- pect (impossibility to evaluate the metrical properties by the sight) and the mathematical aspect (projective geometry, which deals with the graphic properties of the figures). This means that the projective space is the ab- stract of the visual physiological space.
Enriques admits that the problems connected to the way in which the touch functions are more complex than those connected to the sight (Ivi, pp. 184-185). Essentially, these problems derive from the fact that: a) a thre- shold of sensations exists, beyond which the cutis cannot distinguish between two quite near points and a single point; b) a given and constant length is perceived as different in different points of the cutis. The first problem concerns the sight, too. This means that the visual and tactile space is not continuous. The item b) is a funda- mental problem, which potentially, could prevent us to evaluate any distance. This impasse is overcome if one thinks that an estimation of the length of an object needs the reference to a specific tactile organ. This organ is usually our hand. Our hand allows us to distinguish between a plane and a curve surface, more than that: due to the specific and regular kind of sensation they produce, our hand makes us capable to distinguish the circle among the curve lines and the sphere among the curve surfaces. But the circle and the sphere are characterised by a typical distance: the radius. This means that our special muscular-tactile faculty, which finds an expression in the action of the hands, is the physiological way in which we acquire the sense of the distances. In contrast to this, it is difficult to get a tactile-muscular imagine of a straight line or of a plane surface. Hence, the muscular- tactile space gives origin to the metric properties. Thus, the metric of each geometry depends on this kind of physiological space (Ivi, pp. 185-187). For example, Euclidean geometry depends on the visual space as to the theorems which deal only with graphic properties, while it depends on both spaces for the theorems which also deal with metrical properties.
By means of similar reasons, Enriques explains that the general theory of continuum (analysis situs) depends on the general muscular-tactile sensations, not limited to a specific organ as the hand15.
From this analysis a fundamental interpretation of Enriques’ thought follows: the basic, the primary intuition is that given by the three groups of sensations. They offer the perceptive material on which the geometrical space is constructed. However, a link is missing which connects the two kinds of spaces. For, Enriques writes:
“To claim that the geometrical concept of space is the abstract of the different physiological spaces, as to a mobile observer, probably is not yet an exhaustive answer to our question [the origin of the geometrical space] until it is not clarified how the physiological space tends to an almost geometrical representation relative to the observer. This is possible only by association and abstraction. All the dissymetries of the various physiological spaces can be eliminated by their comparison” ( Enriques, 1906, 1925: p. 179 ).
Therefore the situation is like this:
1) Our senses offer a series of sensations which are ordered according to graphic (visual sensations) or metric (muscular sensations) criteria;
2) The geometrical space is a concept which is constructed by our mind in three steps: first of all the mind compares the intuitions provided by the senses; after that it associates the sensations to create a perceptive un- iverse which is not a mere bundle of sensations. This gives origin to our perceptive space, in which we are able to connect the visual with the tactile sensations. Finally, the abstraction from the specific contents of the percep- tive space allows us to reach the idea of a geometrical object in which lines without width and surfaces without thickness exist.
Therefore Enriques is convinced that a scientific approach to the problem of the perceptive space can be reached only by physiology, but the origin of the geometrical space is not only a physiological problem which, to use a modern term, can be explained by the neurosciences. What is important to explain for the genesis of the geometrical space is the way in which a certain mental function operates, not the function in itself. To be clearer: even though an area or a series of areas of the brain were discovered, which is/are the centre/s of functions as the comparison among sensations, the faculty of association and the faculty of abstraction, the problem of the gene- sis of the geometrical space would not have been yet solved because these physiological discoveries―although fundamental for a mapping of our gnoseological faculties―cannot inform us how the perceptive space is trans- formed into a geometrical space by our mind. This is an epistemological position, which is not connected to the fact that the neurosciences were at the beginning when Enriques wrote. The following words by Enriques―re- lated to the phenomenon of the language―are indicative:
“But who does not see how foolish the idea that in the future the science of the language can be reduced to the examination of Broca’s circumvolution is?” ( Enriques, 1906, 1925: p. 39 ).
In Scienza e razionalismo, while arguing against the positivistic and romantic philosophies, both of which― paradoxically―, according to Enriques, converge in the psychologism, we read:
“The researches, to which this philosophical tendency [the positivism] drives, are useful and have an inter- esting scientific meaning. Notwithstanding, they do not reach the aim to catch the most general and ele- vated thought-activities. Rather, they risk to establish some worthless relations of the mental activity with the connected physical and physiological phenomena.” ( Enriques, 1912, 1990: p. 246 ).
Thence, Enriques thinks that the physiological structure offers the intuitive material for the construction of the geometrical space, but the superior mental activities of comparison, association and abstraction―and in particu- lar this last one―can be caught only by an examination of how the mental activity unfolds in the course of his- tory, since the abstract faculty of our mind is something plastic―open to develop in different manners its poten- tialities―, which operates according to the way in which circumstances (in this case the cultural and scientific environment) change16.
Let us summarize the interpretation we give to Enriques’ conception of geometry:
1) A first level intuition exists: it is given by our visual and muscular sensations, which offer a physiological space.
2) The space of the Euclidean geometry, the projective geometry and of the initial propositions of the analysis situs are concepts obtained by abstraction from the first level sensations. The geometrical space is a concept and not an intuition a priori. To confirm this position of Enriques, one could remind the reader that a graphic projec- tive geometry was born in a late phase of history of mathematics, although, from a perceptive point of view, the visual sensations are absolutely fundamental and primary for us. Cultural and historical circumstances play hence a pivotal role.
3) With regard to abstract geometry it was born thanks to the complex development of history of mathematics. The space of abstract geometry is not, however, a mere formal and non-intuitive entity. It is connected to the second level intuition, which is a purely mental intuition. It allows us to imagine, in an almost concrete manner, the models of abstract geometry. They can be obtained by means of analytical procedures, but the intuitive view is useful for them to appear to us as a series of worlds connected by structural similarities, despite the different objects of which they are composed. The second level intuition and the modelization permit to get a synthetic view on these geometrical universes.
Therefore the interpretation of the geometrical space given by Enriques allows us to grasp the profound sense that intuition plays in his conception. It is well known that, according to Enriques, the first level intuition has to provide the material for the axioms, but that, afterwards, the development of the reasoning has to be logic. These passages from the introduction to the Lezioni di geometria projettiva are so clear that no comment is necessary:
“The choice of the fundamental elements of geometry is not given a priori; the elements are chosen which are simpler for the psychological intuition, that is those elements whose notion is formed in our mind as a content of the concept of space. For example: point, straight line, plane. […]. Each other geometrical enti- ties, introduced after the fundamental elements, has to be logically defined by them […]. The study of the geometrical properties proceeds in two ways: 1) by exerting the (psychological) intuition on the spatial concepts; 2) by deducing with the logical reasoning new properties from those given by intuition” (Enri- ques 1898, 1904, 1996, pp. 1-2).
This means the intuition provides the basic concepts and axioms of geometry. Nevertheless, it has also a task, which, in our opinion, gets an even more important role inside Enriques’ conception: the intuition supplies the global sense and meaning to geometry. Beyond the logical aspect of the theory there is an inner coherence, an internal logic of the different geometries, which can be caught only by a global and synthetic vision on them. This can be offered only by intuition, which―as we will see in next section―is connected with the historical development of mathematics and science, not with logic. Enriques writes:
“The reason, which constructs science and which is disclosed in the historical evolution of thought, cannot be explained by means of a purely logical analysis” ( Enriques, 1935, 1983: p. 49 )17.
And again:
“If we want to have a more profound knowledge [of scientific theories] and to realize which are their limits, it is necessary to break the logical framework and to look for the innermost reasons of ideas’ evolution: how from a previous inferior theory, it was possible to construct a superior, wider and more exact theory […]. ( Enriques, 1936, 2004: p. 15 ).
Thence, intuition and history are the pulsing core geometry and, more in general, of science. However, geo- metry, as far as it was one of the first product of the human spirit and since it is directly connected to the basic intuitions has an absolutely prominent role, as we will see.
But: passing from geometry to physics, what is the role of intuition? Once clarified Enriques’ genesis of geo- metrical space and its connections to intuition it is easier to fully catch his conception of physics, to which we have referred in the previous section. With regard to this two considerations are fundamental:
1) the space of the metric geometry can be interpreted taking into account the inner development of geometry. In this case, we are in front of the described picture. But, it can also be considered in the light of the develop- ment of physics. Both analyses are legitimate because the metric space of geometry has this double character: it tends, from one side, to the space of abstract geometry; from the other side to the physical space. In this case the theorems of geometry are only a symbolic expression of physical relations ( Enriques, 1906, 1925: p. 158 ). The theorems of geometry indicate that, according to a certain way to calculate the measures, which depends on the precision of our instruments, the margin of error is undetectable and, hence, some relations, which are not in themselves relations of identity, seem, in fact, to get this aspect. Enriques considers the theorem: “the angles at the basis of an isosceles triangle are equal”. Let us suppose to have three metallic bars, which we consider as the sides of a triangle, and that are some meters long. Furthermore our instrument has a sensibility of 10−3 meters. We measure and check that two bars are equal. This does not mean they are really equal, but that their difference ―which for sure exists―cannot be measured by our instrument. Given this condition, the theorem says that the difference between the two angles at the basis is insensible according to an order of approximation, which de- pends on the precision of the measurement of the bars. The real meaning of the theorem is hence: “if the differ- ence between the two sides of a triangle is less than a quantity ε, the opposite angle will differ by less than a quantity τ, which is a function of ε” ( Enriques, 1906, 1925: pp. 158-159 ). This function can be calculated. Enri- ques adds to clearly explain his position:
“When the theorems of geometry are converted from equalities to inequalities, as seen above, they repre- sent a part of the positional relations among bodies. To complete these relations it is necessary to add, in the single concrete applications, what concerns the nature of these bodies (heath, forces, and so on), which is extraneous to theoretical geometry” ( Enriques, 1906, 1925: p. 159 ).
Therefore no doubt: the propositions of geometry represent a limit-reference point for the propositions of physics. The latter always deal with inequalities. As to geometry, if we have refined means of constructions, when a theorem of geometry concerns an equality, the detectable physical mistake can be made less than that detectable with the means of measure available in a certain epoch. While if a theorem of geometry concerns an inequality, this process is not possible a priori. The theorems of geometry simplify the reality and tend to reveal statistical regularities and identities (Ivi, p. 159). Thence the geometrical space is a prototype of the physical space and expresses as rigorously invariable a series of properties which are, in fact, statistically invariable. This is the physical meaning and function of the geometrical space and it is also clear in what sense Enriques claims that geometry is separated from physics by an abstraction ( Enriques, 1912, 1990: pp. 255-256 ; Enriques, 1938, 1983: p. 55 ).
2) What is the role of intuition in physics? We have seen its role is, according to Enriques, to supply the fundamental concepts and axioms of physics. However, as in geometry the primary intuition has a double role. This is explained in the final sections of Problemi della scienza and we think that the literature did not pay enough attention to this aspect of Enriques’ production. The visual and the muscular intuitions plays a role in the genesis of the geometrical space. But what about physics? Their function is important or better, fundamental. Entire sections of the history of physics can be interpreted as a sort of struggle between visual and muscular conceptions and models. Enriques begins his analysis by dividing the physical data into two kinds: a) geometrical a kinemat- ical data, he calls extensive; b) the dynamical data (the forces), he calls intensive ( Enriques, 1906, 1925: p. 269 ). The data of kind a) can be reconducted to the vision because, although from a geometrical point of view, metric geometry has a muscular-tactile basis, from the physical standpoint geometry and kinematic do not deal with ac- tions and forces, which are the physical expression of the muscular sensations. Therefore a physics which as- sumes the data a) and tries to explain the forces is a physics whose basis is visual; a physics which assumes the data b) and tries to explains the other data, and especially the bonds, by the forces is tactile-muscular (Ivi, p. 269). Enriques claims that the Cartesians followed a model of physics which is exclusively visual, whereas Newton and the Newtonians a model which is mainly―although not exclusively―tactile-muscular. The first example given by Enriques will clarify his though. Let us consider gravity: the idea according to which gravity derives from the collisions of mobile corpuscles (Gassendi, Descartes, Huygens, mentioned by Enriques, we add Leibniz) is a visual theory of gravity. For, when elastic bodies collide there are three moments: 1) motion of the bodies; 2) force produced by the collision; 3) further motion provoked by the force. But, Enriques claims:
“The force […] which has successively the role of “effect” and of “cause”, can be ideally suppressed by those who associate the two moments of the motion, which can be connected to the described collision. In this way, we have a series of visual imagines. If we would know the relations among these imagines, it would be theoretically possible to eliminate―and hence, in this sense―to explain the datum force” (Ivi, p. 271).
Enriques adds that the difficulty is exactly the determination of two successive visual imagines without re- sorting to any tactile-muscular model, but, in itself, the model proposed is visual. Obviously Newton’s concep- tion of gravity is tactile-muscular. Almost the all pages from 269 to 315 of Problemi della scienza interpret im- portant phases of the history of physics in the light of the distinction between visual and tactile-muscular ap- proaches and models.
This is a further confirmation that, according to Enriques, intuition is not limited to provide the basic concepts and propositions for geometry and physics. It produces a series of imagines and models, which, though do not impose a precise development to the theory―the development is, in fact, connected to logic as to geometry, and to hypotheses deriving from experience as to physics―, orientate the research in a certain direction, according to the imagines and models preferred by a geometer or physician.
The intuition is a cornerstone of Enriques’ gnoseology. The other one is history of science. Now we will deal with this subject.
3. History of Science, Birth of Philosophy, Gnoseology: More than a Relationship
In Enriques’ thought these themes are strictly connected. Their analysis will show the fundamental role ascribed by Enriques to geometry (first of all) and to physics for the development of the entire human thought.
3.1. History of Science and Its Features
The different spatial sensations give form to the spatial intuition, on which our mind bases his activity of con- ceptualization, whose highest level is the abstraction. The abstractive process opens a series of possibilities for the development of knowledge and science, but does not trace a necessary path: several paths are open and the description and comprehension of the reason why a certain development occurred is the task of history of ma- thematics and science. This role is fundamental because the human mind is plastic: obviously it produces know- ledge and science, but at the same time its activity is influenced by the way in which science and knowledge are structured in a certain period. There is a mutual influence between development of mind’s activity and actual state of science. This is strictly connected with one of the most known Enriques’ epistemological thesis: science is a series of successive approximations towards the truth18. The truth is a limit-idea, which can never be reached, but to which science tends. History of science deals with the problem of how human mind looks for the truth. Enriques explicitly claims:
“If the truth is only one step towards the truth, the value of science will consist in proceeding rather than in remaining at rest in a reached result. The facts, the laws and the theories will get their sense from their re- ciprocal concatenation and development rather than from science considered as a given and static system. This implies that the ideas have to be explained recognizing their origin and their development, rather than resorting to universal intuitions of mind, which constitute an unconditioned a priori of the thought. The scientific ideas have hence to be expounded in function of the rational necessities related to the need of un- derstand and subordinate a broader reality […]. The historical vision of science appears hence a dynamic vision, which receives from the past a rule to direct its attention to the future” ( Enriques, 1936, 2004: pp. 12-13 ).
This means: history of science participates actively to the construction of scientific reason. Enriques adds that history of science is a prominent part of a Cyclopean enterprise: to explain the mechanism of our intelligence. From these mechanisms also depend the origin of the language and the possibility to communicate the know- ledge from man to man and therefore the possibility of the teaching ( Enriques, 1936, 2004: pp. 16-17 ).
This approach implies a quite peculiar view on history of science, which is absolutely typical of Enriques. The basis to understand a series of his assertions, which, otherwise could appear hazardous and anti-historical is that Enriques is not interested in history of science as a reliquary of the successes obtained by the great mathemati- cians and scientists of the past. He is interested for his necessities of the present19, related to his mathematical, educational or gnoseological researches. Therefore he tends to offer a series of pictures consisting of strong in- terpretations of scientific or philosophical conceptions, to which the literature assigns, in general, a different value than the one Enriques’. In particular, if Enriques is interested in a certain aspect of a doctrine, aspect which has usually been deemed as residual and not significant, he tends to far overestimate the importance of that aspect, because such a doctrine contributed to the development of human reason thanks to that aspect, not because of his entire asset of ideas. We will see a paradigmatic example of this.
Therefore the cornerstones of Enriques’ conceptions of history of science are:
1) The history of mathematics and science is basically history of the scientific ideas. Enriques recognizes the importance of the social factors (see Enriques 1936, 2004: pp. 16-17 ), but to understand the phenomenology of how mathematics and science are developed and hence to fully catch the progress of human reason, the history of scientific ideas is necessary. The philological precision is important, but it has no value, if the scholars ap- proach the historical documents without a clear idea of what they are going to find, and of which the theoretical reasons that led them to study a certain document are. Enriques is clear. For, we read:
“[…] it is particularly important for the mathematician as well as for the philosopher, to catch the genesis and the development of the ideas. This means to construct history of science in its highest meaning. This history touches the origins of geometry and of infinitesimal analysis as well as of logic and metaphysics. It depends―in great part―on the interpretation of the sources, which raises difficulties and disagreements. It is not possible to solve the divergences of opinions by the mere philological erudition without a philosoph- ical view.” ( Enriques, 1924-27b , parte prima, tomo primo, p. 3).
The history of how a train of scientific thoughts was developed is both a history of science and of what we could call a phenomenology of scientific spirit.
2) As a consequence of this view, an objective history of science does not exist. In a section of Il significato della storia del pensiero scientifico, entitled la storia obiettiva di Duhem (“Duhem’s objective history”, Enri- ques 1936, 2004: pp. 42-46 ), Enriques discusses his thesis, considering the way in which Duhem presents histo- ry of science. Duhem claims to offer an objective history because he presents a series of documents with few in- terpretations and hence he leaves the documents speak to reconstruct history. Actually, Enriques claims, Du- hem’s history of mechanics is far from being objective: the first documents used by Duhem are the works by Plato and Aristotle. Since Duhem ignores the entire production preceding or contemporary to Plato, from his documents a certain history of mechanics follow. While, if he had considered (as Enriques does. We will see in next section) the ideas of other authors―in this case Enriques is thinking of Democritus―, a history of mechan- ics different from Duhem’s would have been constructed. This behaviour of Duhem characterizes his history of mechanics after the Greek period, too. This operation by Duhem is idealogical and dangerous as far as it is passed of as objective history, due to the huge amount of documents is used. In contrast to this it is necessary to assert explicitly history of science is not objective and it is based on strong interpretations, which, obviously have to rely upon the documents. Enriques pushes the non-objectivity of history of science till professing that history of science is constructed a priori. He is explicit:
“Let us be allowed to express our opinion by means of a scandalous statement: history of science, as physics-theory, is made a priori, at least to a certain extent. It is, however, necessary to change opinion, to modify our construction, if it is not adherent to the texts, to the sources, the documents and the proofs. […] If the sources do not agree with the rational criterion of research, it is needed to accept their response, with the same spirit with which the theoretical physicist is ready to bow to the results of experience.” ( Enriques & De Santillana, 1932: p. 8 ).
History of science, as theoretical physics, is based on a priori hypotheses―this is Enriques’ conviction―, the documents get in history of science the same role held by the experiments and experiences in physics: according to Enriques, they can falsify an interpretation or a certain theory, but in themselves they cannot produce a new interpretation or a new theory. Their value is limitative, not constructive. Enriques’ view is expressed in a clear manner: the secrets of the universe cannot be discovered by the mere reasoning. Nevertheless, every observation and experience gets a value only if it is framed inside a reasoning ( Enriques, 1906, 1925: pp. 72-73 ). Given the homology between theoretical physics and history of science, the same consideration holds for history of science, too.
3) History of science is also the basis for philosophy. This depends on the particular interpretation given by Enriques of the thought of several pre-Aristotelian philosophers. Enriques thinks that philosophy was born on two bases: a) the comprehension of the abstract character of geometry21 due to Parmenides and Zeno; b) Demo- critus’ physics. This means the knowledge and the correct interpretation of the scientific though are the neces- sary condition to understand the birth of philosophy. Enriques is, once again, clear, as he writes:
“The philosopher will find in the history of scientific thought not only the criteria to judge the value of science, but also the explanation of the order and meaning of the problems of philosophy because in the history of Western civilization those problems rise on the ground of the naturalistic research.” ( Enriques, 1936, 2004: p. 31 ).
The way in which Enriques developed this thesis will show the prominent role of geometry in the develop- ment of the whole Western thought.
3.2. Geometry, Physics and the Birth of Philosophy
We have seen that Enriques explained in details the relations between senses and geometry, distinguished among the different kinds of intuitions involved in geometry and dealt with the difficult epistemological prob- lem concerning the role of the models inside geometry. His detailed analyses are a clear mark that geometry gets an absolutely primary role in the development of human knowledge. The circle of Enriques’ ideas is closed when he tried to show that geometry is even at the basis of the birth of the entire philosophical thought.
His interpretation sounds like this: he reconsiders, develops and tries to justify in a convincing manner some ideas already expressed by Tannery22. In particular: the doctrine of the Pythagoreans was based on the idea of the monad-points. In their opinion the geometrical point was conceived as a sort of indivisible material point, which is smaller than any physical object, but which maintains something as a dimension. If we interpret in this manner the Pythagorean point, the typical assertion that the things are composed of numbers becomes compre- hensible: the points as indivisibles can be numbered, to each point a number can be associated. The matter can be divided into points, hence the bodies can be considered as composed of material points, and therefore of the numbers, which are associated to them. This allowed the Pythagoreans to give a significant inner coherence to their theory. For, they had already discovered that the ratios between numbers were at the basis of the musical harmonies and hypothesized that the movements in the universe were regulated by harmonic ratios, too. Conse- quently they thought to be authorized to consider the numbers as the components of the matter and the relations among numbers as universal laws ( Enriques, 1923: pp. 74-78 ). Thus, Enriques thought that the fundamental step to understand Pythagoreans’ doctrine was the idea that the point was an indivisible. In this manner an insensible transition from the geometrical points to the physical-material points seemed legitimate. Enriques explain with clear words Pythagoreans’ conception of geometry:
“[…] the geometrical figures were not yet abstracted from every matter. Rather, they were as forms of a universal matter, which was thought as an identical component of the sensible matters, although they were different from a qualitative standpoint: as the Pythagorean doctrine drove naturally to interpret the qualita- tive differences as differences in the position and in the number of things’ constitutive elements. That is: as far as the geometrical point appeared as a material point, like a grain of sand, it was already something su- perior in comparison to the merely empiric point.” ( Enriques, 1923: p. 78 ).
Superior and more abstract than the empirical point, but not yet the point of Euclidean geometry. How and why was there this step? To find an answer to this question, Enriques points out that the Pythagorean conception implies that the geometrical figures are composed of points in actu and that hence, each segment should be commensurable. As a consequence of the discovery of incommensurable segments or because of general inner development of geometry, the idea of the monad-point raised a series of difficulties and contradictions, until a new idea of point was gained by Parmenides ( Enriques, 1923: pp. 78-79 ).
It is well known―and it was in Enriques’ epoch―the traditional metaphysical interpretation of Parmenides’ thought: Parmenides wrote against Heraclitus’ doctrine of the becoming. Enriques refuses this interpretation: he reinterprets Tannery’s and Zeller’s idea to translate Parmenides’ locutions τò ἐòν and τò μὴ ἐòν respectively as the Full and the Empty (ivi, p. 79). Given these premises, Enriques translates the following passage of Parme- nides’ Peri Physeos like this:
![]()
Thence Enriques translates τò ἐòν (existing, esistente in Italian) as the space and ἀπέοντα (absent things, le cose assenti, in Italian) as the surfaces. He clarifies that this translation could appear artificial and bizarre for those scholars who have always considered Parmenides a mere metaphysician, not interested in the foundation and clarification of the basic geometrical concepts (Ivi, p. 81). In contrast to this, Enriques thinks that the men- tioned passage is the first one in history of science/philosophy, where the concept of a surface with a length and a width, but without a thickness is expressed, though in outline. This means Parmenides founds rational geome- try, whose objects have anymore nothing to do directly with the material objects.
Enriques explicity claims:
“Therefore the critics to that theory [Pythagorean conception of the point], in the specific way in which it is presented by Eleatic School, is, at the same time, the critics of the geometrical concepts, which makes it possible to edify a rational point having no extension, a line having a pure length and a surface without a thickness.” ( Enriques, 1922b: p. 419 ).
These objects are already those of Euclidean geometry. Enriques’ exegesis also relies upon the interpretation of two Proclus’ passages (Ivi, p. 81). He adds further important specifications: he analyses another fragment by Parmenides (Ivi, pp. 82-83) and reaches the idea that the principle of non-contradiction is expressed for the first time. The necessity for Parmenides to clarify this logical principle is derived, according to Enriques, from the necessity to eliminate the hybrid and contradictory concept of point expressed by the Pythagoreans (Ivi, p. 83). For, the geometrical point cannot be considered a sort of indivisible with a dimension, although as small as possible.
Therefore:
1) Parmenides is the inventor of the modern geometrical concepts.
2) If, as most of scholars think, Parmenides has to be considered the Father of philosophy, this means that the basis of philosophy is the speculations on the geometrical entities.
3) Rational geometry was born as an answer to the hybrid Pythagorean concept of point.
4) The logic itself (principle of non-contradiction) is formulated as a need of geometry. Logic’s origin is geometrical, too.
Coherent with this line of interpretation, is the exegesis given by Enriques of Zeno’s paradoxes: The aim of Zeno was not to show the impossibility of the movement (which, according to Enriques, would be absurd, not paradoxically), rather the absurdity to think the continuum is composed of points. The points can be elements of division of the continuum, but they do not compose it. The paradoxes derive only from this conception of the continuum. If we abandon it, the paradoxes disappear. We summarize Enriques’ idea, which, as he himself un- derlines is in part, due to Tannery (Ivi, p. 85): if any interval―whose lengths are decreasing, according to a cer- tain progression―of an infinite series were composed of discrete points, the sums of infinite intervals, which is necessary to consider in Zeno’s paradoxes, could not converge to a finite interval, because they will be composed of infinite discrete points, whose length should be infinite. From here it is possible to deduce the entire logic of Zeno’s paradoxes (Ivi, pp. 85-86).
This means that Zeno’s paradoxes are born on a geometrical basis in order to confirm the rational conception of geometry sustained by Parmenides against the hybrid Pythagorean theory (Ivi, pp. 83-84).
It is here necessary to summarize the role of geometry inside gnoseology and its history:
1) Geometry derives by abstraction from our basic sensible intuitions. The different branches of geometry are reached by the abstractive activity of our mind. Metric, projective geometry and analysis situs correspond to our primary intuitions. The development of the concept of abstract geometry is related to our secondary intuition.
2) Since the mind is something plastic and connected to the general social and cultural environment the dif- ferent geometries have been developed in different historical periods. History is hence fundamental for geometry and gnoseology.
3) History shows that the birth of philosophy relies upon the birth of rational geometry.
Therefore geometry is the fundamental product of human mind, as far as it is connected with our basic intui- tions and with the birth of science and philosophy in the Western world.
The set of consideration we have expounded until now proves our thesis, according to which the whole gno- seological speculation by Enriques has a geometrical basis.
Since the physical space is close to geometric space and physics and geometry are two sister-disciplines, no surprise that Enriques connected with a strong link the birth of rational geometry (Parmenides and Plato) with the birth of abstract mechanics (Democritus). Enriques dedicated several publications or sections of publications to Democritus22. We do not have room in this paper to supply a profound analysis of Enriques’ speculation on Democritus. This is the material for a future specific paper we are going to publish. However, it is here, at least, necessary to refer to general Enriques’ thesis, which sounds: there is a strong continuity between, from one side, Parmenides’-Zeno’s contributions to rational geometry and in particular their conception of abstraction, this mental activity, which is so important in Enriques’ view and Democritus’ results in mechanics ( Enriques, 1922b: pp. 422-423 ). First Leucippus, but, above all Democritus, developed, from Parmenides, the concept of an ab- stract matter, by considering only the primary qualities (magnitude and form). This is the fundamental concep- tual Parmenidean frame in which Democritus developed his speculation. After that, relying upon the concept of porosity by Empedocles, the concept of the matter as composed by atoms was obtained. In this process the re- placement of the Parmenidean Full with the Empty is fundamental. Democritus further developed the process of idealization till reaching the two fundamental concepts of abstract mechanics: mass and inertia23. Therefore:
Parmenides: Rational Geometry = Democritus: Rational Mechanics
Thence, geometry is the first basis of philosophy; mechanics the second one. Plato’s ontologism, but, maybe even more important, Aristotle’s ideas on forms and matter and his division of the sciences, made philosophy far from its pulsing core and its origin inscribed into the birth of geometry and mechanics ( Enriques, 1922a: pp. 1-46 ).
We add an interpretation to conclude Enriques’ reasoning: geometry is born as an answer to the crisis of Py- thagorean doctrines. In such a crisis the discovery of incommensurability had a prominent role. The incommen- surability is tied to the length of a segment and it derived from the discoveries related to the ratio between side and diagonal of a square. Length, square (and hence right angle) are metric, not projective concepts. In projec- tive geometry quadrilaterals and angles exist, but not squares and right angles. Hence rational metric geometry was born before projective geometry as its was born as a critics to Pythagorean concepts, which were tied to the metric. This is our interpretation, our addition to Enriques’ reasoning, but it is fully coherent with his line of thought.
It is trivially true, but useless, to claim that the geometrical interpretation of Parmenides, the similarities be- tween Parmenides and Democritus as well as the idea that Democritus is the Father of the concepts of mass and inertia are almost surely wrong from a historical point of view24. Nevertheless, they are fundamental to under- stand Enriques’ gnoseology and the role he ascribed to geometry. The other element, which is necessary to fully catch Enriques’ ideas is the examination of his cultural reference points and of the cultural mileu in which he worked. In particular the fundamental items are the following ones: the position of Enriques towards; 1) Kant; 2) Mach and the empiricism; 3) Poincaré and the conventionalism-nominalism-pragmatism; 4) mathematical logic and set theory; 5) quantum mechanics.
On the items 1), 2), 3) there is a certain amount of literature. As to the item 5), Enriques’ book Causalità e determinismo nella filosofia e nella storia della scienza ( Enriques, 1945 ) is a direct reference point, while Enri- ques’ views on set theory and mathematical logic are not so much explored, but they are significant to highlight some aspects of his gnoseology connected to the picture we have described. Because of this we will conclude our paper with a section dedicated to this problem, focusing on set theory.
3.3. Enriques’ Gnoseology, Set Theory, Mathematical Logic
Enriques’ positions with regard to the foundation of mathematics can be divided into three items: 1) foundation of geometry in the second half of the 19th century; 2) Cantorian set theory; 3) development of mathematical log- ic between the end of the 19th century and the 30s of the 20th century.
With regard to item 1), there is no doubt: a) Enriques thought that the whole process, which reached its ideal conclusion with Hilbert’s Grundlagen der Geometrie represented a line of continuity with the development of geometry, starting from the beginning of the 19th century, inside which projective geometry played a prominent role; b) he was absolutely favourable to this development and considered himself to be one of the protagonist of such a process.
Enriques dealt with this problem on several occasions, however Per la storia della logica offers the most complete view of Enriques’ standpoint: he traced a history of logic until the 20s of the 19th century dealing with several problems. A great importance is ascribed to the progressive acquisition of the idea that the mathematical definitions are only nominal, not real (Ivi, pp. 27-30, 74, 78-85). In the 19th century, Enriques identified six events, which contributed to the development of a foundational sensibility: 1) Monge’s and Poncelet’s projective geometry; 2) non-Eculidean geometry; 3) development of the algebra of logic in England; 4) the critics ad- dressed by the positivists to a metaphysical conception of science and mathematics; 5) the debates on the foun- dation of analysis (Enriques mentions Abel, Cauchy, Weierstrass, Bolzano, Du Bois Reymond, Cantor). How- ever, despite the importance of the items 1)-5) the very modern conception of geometry is developed only by the “most recent critical examination of the principles of geometry” (Ivi, p. 131).
The set of conceptual streams involved in the critical thought of geometry are: 6.1) the principle of duality in projective geometry and the use made by Gergonne (Ivi, p. 132-133); 6.2) the theory of the implicit definition, thanks to which a system of concepts is implicitly defined by a system of propositions (axioms, Ivi, p. 134); 6.3) the axiomatization of projective geometry by Von Staudt (Ivi, p. 137); 6.4) the birth of abstract geometry (Ivi, pp. 138-141). All these set of results concerning both geometry and its logical structures converge in the idea that the logic form of the geometrical axioms is exactly that of relations holding a meaning independently from the content of the concepts. Moritz Pasch was the first who fully realized and expounded this approach (Ivi, p. 164). The refinement and the improvement of Pasch’s works was due to mathematicians as Veronese, Enriques him- self, Vailati, Pieri and Padoa. Hilbert, independently of these mathematicians reached the same results, gave them a more complete and systematic form and published them in the Grundlagen (Ivi, pp. 165-167). After that, Enriques expounded in details Pasch’s approach (Ivi, pp. 168-174). The positive judgment expressed towards the transformation of geometry into a hypothetical-deductive system had been already clarified by Enriques in his review to Hilbert’s Grundlagen (See Enriques, 1900 ; Bussotti, 2008b: pp. 83-86 ).
The reason why Enriques was favourable to this kind of studies concern their importance inside mathematics and geometry but also their character, or better, the way in which Enriques interpreted their character. He saw in the whole development of the concept of hypothetic-deductive system the ripest fruit of that intuition of second order of which we have spoken as to abstract geometry. This interpretation is fully coherent with what Enriques wrote in his review to Hilbert’s Grundlagen:
“We conclude this brief outline on the important work we are analysing with a final observation: by study- ing abstract questions of a purely logical nature with the most abstracts methods, the author shows every- where to understand the entire value of the geometrical intuition, both in the choice of the postulates― which is carried out with a lucid evidence―and in the final technical applications.” ( Enriques, 1900: p. 6 ).
Clear: according to Enriques the studies on the logical foundation of geometry have finally brought to that synergy between logic and intuition, which has been one of the most important purposes of the whole specula- tion by Enriques. But … story does not end here.
Enriques’ position towards set theory highlights other aspects of his mentality and approach for the problem of knowledge.
Before any commentary and interpretation, we present the following statements by Enriques on Cantor’s set theory:
1) In the Conferenze di geometria, Enriques referred to the “beautiful Cantor’s researches on set theory”, ex- pounded by Cantor in the Acta Matematica and in the Mathematische Annalen25 (Ivi, p. 39). In particular he fo- cused on famous Cantor’s result, according to which the cardinality of the multidimensional continua is the same as that of a segment of straight line, though the correspondence between a multidimensional continuum and the segment is not continuous.
2) In Problemi della scienza, while dealing with the inconsistencies which can derive from the extension to the infinity of properties which are valid in a finite domain and with the connected problem of an uncritical use of the comprehension principle―Enriques calls these uncritical extensions “transcendent process of definition and reasoning”―, he reminds the reader that Cantor himself discovered paradoxes, whose origin is exactly a non-legitimate use of the comprehension principle26.
3) In a quite important section of Scienza e razionalismo, entitled I giudizi d’esistenza nella critica recente delle matematiche ( Enriques, 1912, 1990: pp. 74-76 ), Enriques adheres to the idea that if mathematical existence is interpreted as a logical existence, it is enough that a concept is not contradictory to admit its existence (Ivi, p. 74). However, the attempt to extend mathematics beyond the effective possibility of a mental construction―that is, the necessity to admit an actual infinite number of mental operations―, lead Cantor to create some concepts which “[…] the critical spirits cannot judge well defined: an example of them is the number alef-one, which corresponds to the concept of the totality of the denumerable series” (Ivi, p. 76, italics in Italian text). In the same pages Enriques referred to the Russell paradox as an example of paradox arising from an uncritical use of the comprehension principle. Anyway Enriques also addressed his critics to concepts as Cantor’s 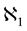 (alef-one), which, in themselves, brought to no explicit contradiction. According to Enriques, the problem is that the theory of the transfinite cardinalities needs an infinite number of mental operations. While only concepts, which can be constructed by a finite numbers of operations are legitimate. Enriques wrote expressly:
(alef-one), which, in themselves, brought to no explicit contradiction. According to Enriques, the problem is that the theory of the transfinite cardinalities needs an infinite number of mental operations. While only concepts, which can be constructed by a finite numbers of operations are legitimate. Enriques wrote expressly:
“It is hence to analyse more profoundly the conceptual construction. It is necessary to point out it always implies a finite number of mental operations. (Transcendent) processes of definition, which imply essen- tially infinite operations, are vicious and conduct to any contradiction” (Ivi, p. 113).
That is: if the mental process needs an infinite number of operations, it is not possible to control the consis- tency of the results, also in the cases―as the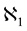 ―in which no explicit contradiction has been detected.
―in which no explicit contradiction has been detected.
4) In 1917 Enriques published a paper on the Revue de Métaphysique et de Morale ( Enriques, 1917 ) con- cerning the mathematical infinity. Here he clearly expressed the following opinion: the realistic conception of mathematics (we call it Platonic conception) is unacceptable and is dangerous as far as the mathematical actual infinity is concerned. That is, the idea that a class of objects is a legitimate mathematical entity only thanks to a definition in wrong. For every property, it is necessary to show that the consideration of the objects subsumed under that property as a class does not generate a contradiction. Till this point Enriques’ opinion does not di- verge from the classical conclusion that the comprehension principle has to be limited by certain axioms to avoid inconsistencies. However Enriques adds this consideration: a demonstration of non-contradiction cannot be―in general―offered by mere logical arguments, it is necessary to create a set of postulates which rely upon a rationalization of experience27. We will interpret this opinion at the end of this section.
5) After having read the strong critics addressed by Enriques to Cantor in Scienza e razionalismo, it is perhaps surprising to read what Enriques wrote in the several pages he dedicated to Cantor in Per la storia della logica ( Enriques, 1922a: pp. 155-160 ). Here he speaks of Cantor as the mathematician who, as to the mathematical in- finity discovered “[…] marvellous and coherent properties, so that any appearance of inconsistency―to use an expression by Bolzano―is really clarified as a mere appearance” (Ivi, p. 155). It is extremely significant that, among Cantor’s papers mentioned by Enriques (see Ivi, p. 155, note 1) the Baiträge zur Begründung der transfi- niten Mengenlehre 1 and 2 appear (indicated by Enriques as “Mathematische Annalen”, Bd. 46, 49 (1895-97), Ivi, p. 155, note 1), where the continuum hypothesis is expounded, in which, obviously, plays a pivotal role. Enriques adds that Cantor’s results have been obtained relying upon a realistic philosophical conception, but this does not question the validity of the mathematical results (Ivi, p. 155). With regard to the problems connected to set theory’s paradoxes, Enriques interprets them as the impossibility to realize some operations concerning the maxima in the series of cardinals and ordinal numbers, but not as antinomies, which mine the coherence of Cantor’s results. However, he adds an interesting consideration: the paradoxes (also including Russell’s) only testify that the realistic philosophical view is wrong. It does not testify an incoherence of set theory as a branch of mathematics (Ivi, pp. 159-160). We will clarify in our interpretation what Enriques meant.
6) The paper I numeri reali is important in this context. It was published for the first time in 1912 as a rework of a previous and far briefer paper written in 1911. In 1924-27 a final version was published ( Enriques, 1924- 27a ). We refer to this version. Enriques expounds several aspects of Cantor’s set theory, but the most interesting considerations concern a fundamental axiom of post-Cantorian set theory: Zermelo’s axiom of choice, formu- lated for the first time by Zermelo in 1904 ( Zermelo, 1904 ). Enriques claims that the possibility to carry out an infinite number of arbitrary choices transcends the faculty of the human thought, unless a rule exists, which de- termines a priori the choices in function of a finite number of operations ( Enriques, 1924-27a: p. 256 ). This pos- sibility cannot be given for granted. Zermelo has decided to pose such a possibility as an axiom. However, Enriques continues, a postulate can only express a set of conditions, which limits the possibility to carry out some operations for the objects to which the postulate is applied28. Therefore, it is not legitimate to apply Zer- melo’s axiom of choice to classes defined independently of this axiom ( Enriques, 1924-27a: p. 257 ). With re- gard to Cantor’s continuum hypothesis and to the use of Zermelo’s axiom to solve it, Enriques claims this use is not legitimate “because, not only the possibility to carry out an infinite number of choices by the thought is as- sumed, without the existence of any external criterion is ensured. But also these operation are extended beyond the denumerable, in a transcendently infinite manner. Transcendent presuppositions, like this, have produced typical paradoxes in set theory” (Ivi, p. 271). In a dense and important note Enriques―also referring to Beppo Levi’s ideas―pointed out, once again, that the axiom of choice does not pose any restrictive condition on the continuum, which is completely defined by its postulates. On the other hand, if this axiom refers to a series of mental operations, Enriques claims ironically that those operations are not typical of every mind (Ivi, p. 271, note 1).
How to interpret this complex series of Enriques’ statements concerning set theory? The situation is rather complex: Enriques appeals to the fact that each new mathematical entity has to be introduced by definitions or axioms for which either a finite number of mental operations are necessary or an infinite number, under the con- dition that a constructive rule is given. In mathematical terms, this means to provide a precise procedure or a function that allows us to construct the new entity. In this case, we think that history of mathematics plays a role, too. For, if a certain entity is directly connected to entities, methods and procedures already used in mathematics, its introduction is not problematic, otherwise the mentioned constructive steps are necessary. To be clearer: Cantor’s results on the identity between the cardinalities of the multidimensional continua and a segment of straight line are considered as a great progress by Enriques because they are based on the consideration of the points composing the figures as sets. This is not problematic for Enriques because something similar―even though, obviously not identical―existed in classical mathematics, too. It is trivial that if we project perspective- ly two dotted straight lines from a centre, a biunivocal correspondence is created in which two segments of dif- ferent length correspond each other. Furthermore, the reciprocities offer an example of correspondence between entities with a different dimension. Therefore, mathematics, though in different contexts and for different aims, offered something, which permitted to consider Cantor’s result valid without the need of any particular further logical-constructive justification. The same consideration is true for the introduction of the first transfinite or- dinal and cardinal numbers, ω and , respectively. These entities are not problematic because ω is considered as the limit to which the series of all the intergers tend. No one had this idea before Cantor, but it is acceptable because it is based on a well known series―the integers―and a well known procedure―the passage to the lim- it-. Mutatis mutandis, the same reasoning is valid for
, respectively. These entities are not problematic because ω is considered as the limit to which the series of all the intergers tend. No one had this idea before Cantor, but it is acceptable because it is based on a well known series―the integers―and a well known procedure―the passage to the lim- it-. Mutatis mutandis, the same reasoning is valid for . Enriques also admits that the operations which allows Cantor to construct the series of the ordinal transfinite numbers are legitimate. Things completely change when Cantor passes from the series of the transfinite ordinal numbers to the first class of the transfinite ordinal num- bers. The operation which consists in considering the ordinal numbers as a new whole, a new set is not a priori legitimate: they are new entities in mathematics and there is no guaranty that any contradiction arises from this operation. Enriques addressed the same kind of critics to Zermelo’s axiom: it deals with transcendent operation without providing any construction or justification these operations are legitimate. Furthermore―as we have seen―Enriques seems to consider the paradoxes of set theory (Cantor’s, Burali-Forti’s, Russell’s paradoxes) on a level with the problem of the legitimacy of Zermelo’s axiom of choice. While, in general, the two kinds of questions are separated, as the paradoxes of the naïve set theory―deriving from an uncritical use of the com- prehension principle―are usually considered as solved by Zermelo’s axiomatization in 1908 (see Zermelo, 1908 ), and in particular by the axiom of separation. While the attempts to limit the transcendent character of the axiom of choice were still alive when Enriques published the final version of the paper I numeri reali. For, he mentions an attempt by Hilbert and the critics addressed by Cipolla, these ones written in 1923 ( Enriques, 1924-27a: p. 271, note 1 ). Therefore, Enriques’ considerations concern a recall to the controllability of the ma- thematical results. Enriques is not an intuitionist à la Brouwer29, neither a constructivist: we have seen he ac- cepted and participated actively to a certain formalization of geometry. Nevertheless, he accepted such a forma- lization because the axioms, although for many aspects were completely different from Euclid’s, maintained the character to limit the mathematical means usable inside a theory. Axioms as that of choice as well as the consid- eration of the series of transfinite ordinal numbers as a set hold a completely different character, that is a tran- scendent character and do not allow the reason to control the results deriving from them. In other words: there is no kind of intuition, either primary or secondary to which they can be reconducted or of which they can induce the utilization. Thence, if no further constructive argument can be forwarded to justify their validity, they have to be rejected. Because of this, Enriques way of thinking is extraneous to the whole development of axiomatic mathematical logic and set theory starting from the 10s of the 20th century.
. Enriques also admits that the operations which allows Cantor to construct the series of the ordinal transfinite numbers are legitimate. Things completely change when Cantor passes from the series of the transfinite ordinal numbers to the first class of the transfinite ordinal num- bers. The operation which consists in considering the ordinal numbers as a new whole, a new set is not a priori legitimate: they are new entities in mathematics and there is no guaranty that any contradiction arises from this operation. Enriques addressed the same kind of critics to Zermelo’s axiom: it deals with transcendent operation without providing any construction or justification these operations are legitimate. Furthermore―as we have seen―Enriques seems to consider the paradoxes of set theory (Cantor’s, Burali-Forti’s, Russell’s paradoxes) on a level with the problem of the legitimacy of Zermelo’s axiom of choice. While, in general, the two kinds of questions are separated, as the paradoxes of the naïve set theory―deriving from an uncritical use of the com- prehension principle―are usually considered as solved by Zermelo’s axiomatization in 1908 (see Zermelo, 1908 ), and in particular by the axiom of separation. While the attempts to limit the transcendent character of the axiom of choice were still alive when Enriques published the final version of the paper I numeri reali. For, he mentions an attempt by Hilbert and the critics addressed by Cipolla, these ones written in 1923 ( Enriques, 1924-27a: p. 271, note 1 ). Therefore, Enriques’ considerations concern a recall to the controllability of the ma- thematical results. Enriques is not an intuitionist à la Brouwer29, neither a constructivist: we have seen he ac- cepted and participated actively to a certain formalization of geometry. Nevertheless, he accepted such a forma- lization because the axioms, although for many aspects were completely different from Euclid’s, maintained the character to limit the mathematical means usable inside a theory. Axioms as that of choice as well as the consid- eration of the series of transfinite ordinal numbers as a set hold a completely different character, that is a tran- scendent character and do not allow the reason to control the results deriving from them. In other words: there is no kind of intuition, either primary or secondary to which they can be reconducted or of which they can induce the utilization. Thence, if no further constructive argument can be forwarded to justify their validity, they have to be rejected. Because of this, Enriques way of thinking is extraneous to the whole development of axiomatic mathematical logic and set theory starting from the 10s of the 20th century.
The examination of Enriques’ position towards mathematical logic would constitute a further section, for which we do not have room. However, a general consideration, which spread a further light on Enriques’ gnose- ology is necessary: a real comprehension of the logical processes of mathematics could not derive from a doc- trine as the mathematical logic, but only by a revisitation of history of mathematics itself and by an analysis of our mental processes. Because of this, Enriques explicitly claims, more than once, that logic is the study of how our mental processes involved in the construction of exact sciences are edified and function (see, for example, Enriques, 1922a: p. 121 ). Therefore, this connects logic to mathematics and physics, the two exact sciences par excellence. While mathematical logic, especially in the most abstract development of the 20th century is some- thing alien to the living mathematics. In 1935 Enriques wrote:
“I indicated the doubts, which concern the empiricism, or at least the restrictions, without which I cannot accept this doctrine. I have more doubts on the logicism. The reason, which constructs science and which is revealed in the historical evolution of the thought, cannot be explained by means of a merely logical analy- sis.” ( Enriques, 1935, 1983: p. 49 ).
Enriques remained, in substance, extraneous to the development of mathematical logic and set theory.
4. Concluding Remarks
In these conclusions, we will summarize Enriques’ gnoseology by points, adding some explanations, where ne- cessary:
1) Geometry is the basis of the gnoseology. This is due to a physiological and historical reason: from a physi- ological standpoint, geometry relies upon our basic intuitions. From a historical standpoint, geometry was the first branch of mathematics to be developed. The aim for rational geometry also marked the beginning of phi- losophy.
2) From a historical point of view, metrical geometry was developed before projective-graphic geometry, al- though the sight is our simplest and fundamental sense. This depends on the fact that the three main functions of the mind: comparison, association, abstraction are exactly functions, not a priori intuitions. This means that they offer a series of possible developments for the mind to construct the concepts (the geometrical and the physical spaces are concepts, according to Enriques), but do not impose a precise form to notions as space and time and to the critical thought about them. Historical circumstances cooperate with mind’s function to the con- struction of concepts and theory. The mind is plastic. It offers potentialities, do not determine.
3) The space of geometry is obtained by abstraction from the physiological space. The space of physics can be interpreted as having a double origin: it is more abstract than physiological space, hence, starting from the intui- tions, it is necessary an abstraction from some properties. For example, the material point of Newtonian physics is less abstract than the point of geometry because it has a mass, but is less concrete than―for example―a grain of sand because it has no dimension. While, reaching the physical space from the geometric space it is ne- cessary to make it more concrete, adding properties as the mass.
4) Given these considerations, it is comprehensible that Enriques criticized many conceptions by Kant. Enri- ques’ entire critics to Kant moves from the idea that Kant is responsible of a usteron-proteron: he had in front of him the successes of the Newtonian physics and he had the intention to find a philosophical doctrine, which gave an absolute value to Newtonian science. The whole structure of the Kritik der reinen Vernunft depends on this. In particular the transcendental value of the a priori intuitions of space and time, which should offer an ab- solute concept of these two entities. Therefore the real a priori is the formed science and Kant offers a justifica- tion, which is, in fact, a posteriori. The high probability that physical space is not an Euclidean space falsifies, according to Enriques, Kant’s doctrine. This is the basis for all the other considerations by Enriques on Kant30.
5) Inside Enriques’ theory of knowledge a further important element is the critics to Poincaré. The two mathe- maticians share the idea that the geometrical space in a concept. Nevertheless, according to Enriques the physi- ological space is closer to geometrical space than in Poincaré’s view. For, Enriques identified the three faculties of the mind (comparison, association and abstraction), while, according to Poincaré, a more complex mental structure exists, which provides the mathematical concept of group of transformation. Only at this stage, the ab- stract concept of geometrical space is formed. The fact that the geometrical space is not strictly connected to the physiological space drove―according to Enriques―Poincaré to the conventionalism, which Enriques criticized on several occasions. For, he thought this conception risked to arrive at the nominalism and the pragmatism, two philosophical tendencies, which deny any theoretical value to truth and science31.
6) For Enriques’ gnoseology, the other fundamental reference point is Mach. Enriques shared many ideas ex- pressed by Mach: a) his idea that, to understand science, it is necessary to start from science itself; b) the method, through which he reached a critical analysis of many scientific concepts (absolute space, absolute time, inertia principle, mass, cc.). Even though, in some cases, he did not agree with Mach’s analysis, he was sympathetic with his methodology, based on a perspicuous examination how the concepts were used in science; c) the im- portance of experience inside the genesis of scientific concepts; d) the value of history of science as the funda- mental reference point to understand the nature of science, independently from metaphysical presuppositions. Nevertheless, Enriques was not an empiricist. He criticised Mach, as he had underestimated the important of our spirit and intuitions. He agreed with many aspect of Mach’s critics to the causality principle, but, after all, Enri- ques thought that a form of this principle is necessary in science32. Thing could be expressed like this: Mach thought that for the comprehension of the development of our knowledge, history of science plus physiology (also considered as experimental psychology) is enough. It is a mistake to refer to mental functions which are not directly detectable in our psycho-physical structure because this means to introduce metaphysical elements in the theory. Enriques recognised the danger of the a priori. Notwithstanding, he thought that the three mental activities necessary to develop the knowledge could not be reduced to a mere historical-physiological fact. An a priori functionality of mind, which depended on the physical structure of the brain, but which could not be reduced to it, still exists in Enriques, not in Mach. We could speak of a Kantian residue in Enriques.
7) Given the plasticity of mind, namely the fact that the functions of the mind express potentialities and not necessities, the reality cannot be considered as something given once and forever. In different stages of history of science, our interpretation and comprehension of the physical reality change. Thence, reality is constructed by the rational coordination of our mind. Science is based on hypotheses, which are preordained dispositions of fu- ture experiences. In this sense, with the progress of science, successive hypotheses are introduced, which pro- gressively offer more precise pictures of the reality ( Enriques, 1912, 1990: pp. 18-21 ). This means that science will never offer a perfect comprehension of reality, but progressively improving comprehensions. The perfect comprehension gets hence the value of a limit-concept. Given: 1) the importance of experiments in providing new hypotheses; 2) the necessity to rationally coordinate such hypotheses, science is an experimental rational- ism, which was already clear to Newton (Ivi, p. 102).
The purposes of this paper are two. One more specific and one more general.
Specific: we have shown in details the role of geometry inside Enriques’ gnoseology.
General: to supply an overview of Enriques’ gnoseology and epistemology in a particular perspective given by our conviction concerning the pivotal role of geometry.
NOTES
1For a synthetic, but clear explanation of the way in which algebraic geometry was developed in Italy between the second half of the 19th century and the beginning of the 20th century, see Ciliberto, 2008 . For the following development of algebraic geometry in Italy, see Brigaglia & Ciliberto, 1998 . See also Conte & Ciliberto, 2004 .
2Many projective properties were already proved in Apollonius’ Conics and the Renaissance studies on perspective deal with projections. Nevertheless, Desargues first studied the projective properties in a systematic manner. As to Desargues’ works, see Desargues, 1951 and Desargues, 2011 . As to the literature, without any claim to be exhaustive, we mention: Andersen, 1991 ; Catastini & Ghione, 2005a ; Catastini & Ghione, 2005b ; Field & Gray, 1987 ; Hogendijk, 1991 ; Le Goff, 1993 ; Le Goff 1994 ; Le Goff, 2005 ; Lenger, 1950 ; Swinden, 1950 . With regard to the whole history of geometry a fundamental reference point is Chasles, 1837 .
3During the 18th century some developments of projective geometry had applications in physic and in particular in new applied mechanics, too. As to this, see Pisano & Capecchi, 2013 .
4For a scientific biography of Enriques, see Israel, 1993 ; Bottazzini, 2001 ; Nastasi, 2010 . An informative paper on the years Enriques spent in Bologna, where the relation between philosophy and mathematics in Enriques is also dealt with, is C. Ciliberto & Gario, 2012 . Many pieces of information on Enriques can be drawn from the site of the National Edition of Enriques’ Works. See http://enriques.mat.uniroma2.it/. In this site, there is a section in which the titles of all the works by Enriques are referred to and a section containing several indications concerning the literature.
![]()
5The literature on Enriques’ gnoseology and philosophy is rather conspicuous. We mention: Badaloni, 1982 ; Bussotti, 2004 ; Bussotti, 2006 ; Castellana, 1982 ; Castellana, 2004a ; Castellana, 2004b ; Cenci, 1984 ; Ciliberto, 1982 ; Geymonat, 1989 ; Israel, 1998 ; Lolli, 1998 ; Minazzi, 2005 ; Parrini, 1999 ; Polizzi, 1982 ; Pompeo Faracovi, 1982 ; Pompeo Faracovi, 1983 ; Pompeo Faracovi, 1998 ; Sava, 2004 ; Simili, 1987 ; Stöltzner, 1998 ; Toscano, 2007 ; Toth, 2004 ; Witkowski, 1986 .
6The whole volume Bussotti (Ed.), 2008 is dedicated to Enriques as a prominent figure of the European cultural milieu to which we refer in the running text. Each paper in this volume also provides an abundant literature on the subject.
7With regard to Enriques’s works on the interpretation of Greek philosophy in the light of his geometrical exegesis, see: Enriques, 1918a ; Enriques, 1918b ; Enriques, 1920 ; Enriques, 1921 ; Enriques, 1922a, first chapter ; Enriques, 1922b ; Enriques, 1923 ; Enriques, 1925 ; Enriques, 1926 ; Enriques & de Santillana, 1932 ; Enriques, 1935 ; Enriques, 1936 ; Enriques, 1938 ; Enriques (posthumous) & Mazziotti, 1948 . Enriques’ classical work on Kant is Enriques 1938, 1983 , although several references to Kant are present in all the works in which Enriques deals with history of philosophy and epistemology. The work in which Enriques expounded his conception of history of science in a clear manner is Enriques 1936, 2004 . With regard to the literature on Enriques as historian of science, see: Bettica-Giovannini, 1989 ; D’Agostino, 1988 ; Freguglia, 1998 ; Galuzzi, 1984 ; Galuzzi, 1998 ; Metzger, 1935, 2004 ; Pompeo Faracovi, 2004 ; A Rossi, 2004 ; Rossi, 1989 ; Sava, 2004 . A volume specifically dedicated to the history of science in Enriques is Castellana and A Rossi (eds), (see Enriques, 1936, 2004 ). As to this text, we remind the reader that Il significato della storia del pensiero scientifico by Enriques was first published in French in 1934.
8This assertion will be clarified in the second section of our paper.
9With regard to the literature on Enriques’ ideas concerning mathematics education and, more in general, on the didactical problems in mathematics faced between the second half of the 19th century and the initial years of the 20th century and connected to Enriques’ work, we remind the reader (without any claim to be exhaustive, and mainly focusing on Italian situation): Bolondi, 2005 ; Borgato, 2006 ; Bussotti, 2012a ; Bussotti 2012b ; Bussotti, 2013 ; Cauterio & Gerla 1988; Di Sieno, 2006; Giacardi, 2006a ; Giacardi, 2006b ; Giacardi, 2010 ; Giacardi, 2012 ; Moretti, 2003 ; Pepe, 2006 ; Tomasi, 1982 . For specific and conspicuous indications concerning literature see Bussotti, 2013 ; Giacardi 2006a ; Giacardi, 2012 .
![]()
10 Vesentini, 2004 . In particular, pp. 13-14.
![]()
11We will deal with the genesis of these concepts in section 2.3.
12See, without any claim to be exhaustive: Castellana, 2004a ; Castelli Gattinara, 2004 ; Fabri, 1982; Taglianini, 1982 ; Villaggio, 2006 .
![]()
13With regard to the relations between Enriques and the formalists and, in particular, Hilbert, see Bussotti, 2008b .
![]()
14On that one can see an account of the role played by geometry in physics ( Pisano & Casolaro, 2012 ).
![]()
15For an explanation of how, according to Enriques, the density and continuity of the straight line is perceptively regained, see Bussotti, 2006: pp. 66-68 . We do not have room here to face this subject.
16The section 3.1. of this paper is specifically dedicated to the role of history of geometry and science inside Enriques’ gnoseology and epistemology.
![]()
17For the problem of the internal logic in Enriques, see Bussotti, 2008b: pp. 94-97 .
![]()
18On this problem, see Bussotti, 2006 , chapter “La filosofia di Federigo Enriques”, pp. 57-102, in particular the section titled “Il ruolo della storia della scienza nella filosofia di Enriques”. In a slightly different perspective, see Nastasi, 2010 . The author concentrates on the evolutionary character of Enriques’ epistemology.
![]()
19Enriques’ idea that history is moved by a present interest and that the historian constructs history has some similarities with the ideas expressed by one of the most inflexible adversaries of Enriques as a philosopher: Benedetto Croce; see, among other works, Croce 1917, 2007 . As to the relations Croce-Enriques, see Pompeo Faracovi, 1984, 2012 .
![]()
20Obviously the word “abstract” is used here only to indicate that the objects of Euclidean geometry are abstract, non-physical objects. This word is not used in reference to modern abstract geometry.
21The work by Tannery to which Enriques often refers is Pour l’histoire de la science hellène, published in 1887. See, for example, Enriques 1923: p. 73 .
![]()
22We remind here the reader the two most important publications or part of publications concerning Democritus: a) Enriques, 1922a: pp. 30-40 and Enriques (posthumous) and Mazziotti, 1948. In any work by Enriques on Greek philosophy, there are references to Democritus.
23See, for example, Enriques, 1922a: pp. 31-32 .
24As to this consideration, we agree with Galuzzi, 1982.
![]()
25 Enriques, 1894-1895: p. 39 . For Cantor’s works to which Enriques was referring, it is quite likely he is thinking of the famous series of contributions Über unendliche lineare Punktmannigfaltigkeiten, published between 1879 and 1884 in the Mathematische Annalen (see Cantor, 1932: pp. 139-246 ). With regard to the papers appeared in the Acta Mathematica, Enriques is probably referring to two works on set theory published by Cantor in French (see Cantor, 1932: pp. 247-260 ). It is, however, worth underlying that Cantor’s result of which Enriques speaks in the Conferenze―that is the biunivocal correspondence between the multidimensional continua and the linear continuum― was proved by Cantor in a paper published in the Crelles Journal in 1878 (see Cantor, 1932: pp. 119-133 ).
26 Enriques, 1906, 1925: p. 15 . Enriques is referring to paradoxes dealt with by Cantor in his letters to Dedekind (See Cantor, 1932: pp. 443-450 ).
27Enriques’ original words in French are: “Une démonstration de ce genre ne saurait être fournie généralement par devra arguments logiques, mais devra faire appel à des postulats empruntés à une rationalisation de l’expérience” ( Enriques, 1917: p. 163 ).
![]()
28It is necessary to explain Enriques’ thought. Some examples will clarify the situation: the axioms of Euclidean geometry limit the operations to those, which can be carried out by rule and compass; the axioms of projective geometry limit the operations to projections and sections and so on.
![]()
29On Enriques and the intuitionism, see Nurzia, 1979: pp. 157-193 .
![]()
30See specifically, Enriques, 1938, 1983: pp. 51-56 . On the relations Enriques-Kant see, among other works; Bussotti, 2006: pp. 57-116 (several references); Israel, 1998: pp. 19-43 ; Pompeo Faracovi, 1983 , in Enriques 1938, 1983: pp. 1-44 (this is the introduction to the mentioned volume); Pompeo Faracovi, 1998: pp. 45-72 .
31For the critics by Enriques to Poincaré’s conventionalism, see Enriques, 1906, 1925: pp. 154-157 ; Enriques, 1912, 1990: pp. 18-26 ; Enriques, 1924-27, 1982: parte I, tomo II, p. 439 ; Enriques, 1938, 1983: p. 55 . On Enriques and Poincaré, we mention, without ant claim to be exhaustive: Bussotti, 2006: pp. 69-79 and 111-116 ; Castellana, 2004a (several references); Castellana, 2008 ; Castelli Gattinara, 2008 ; Cenci, 1984 ; Israel, 1992 ; Polizzi, 2008 ; Polizzi, 2012 .
32Among other passages where Enriques deals with this problem, we think Enriques, 1938, 1983: pp. 61-66 is quite significant to clarify his position as to the concept of cause and to his criticisms―which are of opposite meaning―to Kant and to Mach. The Austrian physicist was one of the main reference-point of Enriques. Problemi della Scienza gives the impression to be an answer to Mach’s Mechanik (See Mach 1983, 1919 ). The structures of entire chapters as la Meccanica and Estensione della Meccanica seems to be directly referred to chapters of the Mechnanik. See also Enriques, 1922a: pp. 130-131; 144-150; 241-244; 254-261 . As to literature, see Bussotti, 2006: pp. 89-102 .