On the Hybrid Model of Nerve Pulse: Mathematical Analysis and Numerical Results

Alexander Mengnjo, Jake Leonard Nkeck

Department of Mathematics, Faculty of Science, University of Buea, Buea, Cameroon.

DOI: 10.4236/jamp.2023.118152                

Abstract

Amongst the important phenomena in neurophysiology, nerve pulse generation and propagation is fundamental. Scientists have studied this phenomena using mathematical models based on experimental observations on the physiological processes in the nerve cell. Widely used models include: the Hodgkin-Huxley (H-H) model, which is based entirely on the electrical activity of the nerve cell; and the Heimburg and Jackson (H-J), model based on the thermodynamic activity of the nerve cell. These classes of models do not, individually, give a complete picture of the processes that lead to nerve pulse generation and propagation. Recently, a hybrid model proposed by Mengnjo, Dikandé and Ngwa (M-D-N), takes into consideration both the electrical and thermodynamic activities of the nerve cell. In their work, the first three bound states of the model are analytically computed and they showed great resemblance to some of the experimentally observed pulse profiles. With these bound states, the M-D-N model reduces to an initial value problem of a linear parabolic partial differential equation with variable coefficients. In this work we consider the resulting initial value problem and, using the theory of function spaces, propose and prove conditions under which such equations will admit unique solutions. We then verify that the resulting initial value problem from the M-D-N model satisfies these conditions and so has a unique solution. Given that the derived initial value problem is complex and there are no known analytic techniques that can be deployed to obtain its solution, we designed a numerical experiment to estimate the solutions. The simulations revealed that the unique solution is a stable pulse that propagates in the x-t plane with constant velocity and maintains the shape of the initial profile.

Keywords

Nerve Impulse, Nerve Pulse Propagation, Hodgkin-Huxley Equation, Korteweg-de Vries Equation, Heimburg Jackson Model, Neurophysiology

1. Introduction

The mechanisms and properties for Nerve pulse generation and propagation form one of the most investigated physiological activities in Neuroscience [1] - [11] . The modelling of this process is historically related to the analysis of action potentials (pulse like voltage waves that carry information along a nerve fiber) whose measurements by electrophysiological techniques have well documented references. The Hodgkin-Huxley model [1] was one of the earliest mathematical models that described and captured the propagation of an asymmetric pulse in the nerve fiber. Hodgkin and Huxley showed how measurements of the conductive parameters of a nerve fiber can be used to directly calculate both the shape and velocity of an action potential on a Squid’s giant axon. According to their model, the nerve pulse is a self-regenerative wave associated with the electrochemical activity of the nerve cell and due to the flow of Sodium and Potassium ions through the protein pores on the nerve membrane. It is now well established that during the generation and transmission of the nerve impulse, the leading edge of the depolarization region triggers adjacent membranes to depolarize causing a self-propagation of the excitation, related to the transmembrane potential, down the nerve fiber [1] [12] [13] . As suggested by Hodgkin-Huxley, a convenient way to describe the nerve impulse propagation is to think of the nerve fiber as an electrical transmission line. Thus, in its most conventional formulation, the Hodgkin-Huxley electrical model assumes currents in intracellular and extracellular fluids to be ohmic so that the net transmembrane current is the sum of ionic (due to the flow of Sodium and potassium ions) and capacitive currents (due to the charge stored on the membrane capacitor). The conservation law for current flow across the membrane was modelled by the equation [1] :

$C_m\frac{\partial V}{\partial t}=D\frac{{\partial }^{2}V}{\partial x^2}-F\left(V\right)\mathrm{,}$ (1)

where V is the transmembrane voltage (action potential), C_m the membrane capacitance, D the diffusion coefficient and F is a contribution of ion currents.

Besides the well-established electrical activity of the nerve membrane, there are experimental evidences [14] - [19] of existing mechanical forces acting on the membrane [21] that are also contributing to the nerve impulse generation [20] . To this last point, it is assumed that the fluids surrounding the nerve cytoplasm induce a sound-like wave when crossing the membrane (Osmotic flow across lipid membranes) and the feedback process governing this flow is represented by a nonlinear dependence of the sound on the net density difference of fluids across the membrane [7] . To describe the formation of density pulses associated with mechanical constraints acting on the nerve membrane, there have been proposals to include nonlinearity in the membrane compressibility together with dispersive effects related to the ladder structure of the nerve fiber [20] . In this respect a nonlinear mathematical model including dispersions was proposed by Heimburg and Jackson [7] , and later on extended by several authors (see e.g. ref. [11] ). The underlying equation, considering a one-dimensional density pulse propagating along a biomembrane of a cylindrical shape, has been modelled by [7] [11] :

$\frac{{\partial }^{2}u}{\partial t^2}=c_0^2\frac{\partial }{\partial x}\left[\left(1+pu\right)\frac{\partial u}{\partial x}\right]-h\frac{{\partial }^{4}u}{\partial x^4}\mathrm{,}$ (2)

where u is the density difference between fluids across the membrane, c₀ is the speed of sound in the homogeneous regime (i.e. in the absence of pressure waves), h and p are constants [20] (hereafter we shall set $p=-1$ for simplicity, [11] ).

Given the evident simultaneous contributions of both electrical and mechanical activities of the nerve in the generation of the action potential, a better description of the generic mechanism of the action potential requires a full account of these two activities.

In [22] , a mathematical model which combines the two nonlinear partial differential equations, namely the one describing the spatio-temporal evolution of the density pulse across the membrane, and the H-H cable equation with a feedback from ion flows across the nerve membrane represented by a density-dependent membrane capacitance was proposed. Properties such as the steady-state regime of the model were considered and exact soliton solutions determined.

In the current paper we consider the non-steady state regime of the model proposed in [22] from a more analytic and mathematical stand point. We establish an appropriate mathematical framework to handle such complex equations and, formulate and prove conditions under which such an initial value problem will admit a unique solution. We then use the results from the framework to verify that the modified model in the non steady state will have a unique solution. Finally, a numerical experiment is designed to estimate the solutions in the non steady state regime and check the stability of these solutions as they propagate in the x-t plane.

2. The Model

In [22] , Mengnjo, Dikandé and Ngwa formulated a model of the nerve impulse taking into account the mechanosensory processes of the nerve cell. In their formulation, the influence of mechanotransduction processes on the generic mechanism of the action potential is investigated analytically by translating to a mathematical model that consists of two coupled nonlinear partial differential equations. The coupling equations are: the Korteweg de Vries equation governing the spatio-temporal evolution of the density difference between intracellular and extracellular fluids across the nerve membrane, and a modified Hodgkin-Huxley cable equation for the transmembrane voltage with a diode-type membrane capacitance. The membrane capacitance is assumed to vary with the difference in density of ion carrying intracellular and extracellular fluids thus ensuring an electromechanical feedback mechanism and consequently an effective coupling of the two nonlinear equations. The equations in [22] are:

$C_m\left(x,t\right)\frac{\partial V}{\partial t}=D\frac{{\partial }^{2}V}{\partial x^2}-\kappa u\left(x,t\right)V,x\in \left[0,L\right],t>0,$ (3)

$\frac{\partial u}{\partial t}=6u\frac{\partial u}{\partial x}-\frac{{\partial }^{3}u}{\partial x^3},s\in \left[0,T\right]$ (4)

$u\left(x,0\right)=u_0\left(x\right).$ (5)

With the help of the exact one-soliton solution, $u\left(x\mathrm{,}t\right)={\text{sech}}^2\left(x-4t\right)$ , of the density difference equation, Equation (4), the cable equation, Equation (3), becomes

$\frac{\partial V}{\partial t}-\frac{2D}{1+\tanh \left(x-4t\right)}\frac{{\partial }^{2}V}{\partial x^2}-\frac{4\epsilon {\text{sech}}^2\left(x-4t\right)}{1+\tanh \left(x-4t\right)}V=\mathrm{0,}$ (6)

where V is the transmembrane voltage. Taking $u_0\left(x\right)={\text{sech}}^{2}x$ , the first three bound states of the model (3)-(5) are [22] :

$V_1\left(x\right)=\tanh x,D=2\epsilon ,$ (7)

$V_2\left(x\right)=\frac{1}{2}\left(3{\tanh }^{2}x-1\right),D=6\epsilon ,$ (8)

$V_3\left(x\right)=\frac{1}{2}\left(5{\tanh }^{2}x-3\right)\tanh x,D=12\epsilon .$ (9)

Here, we address the issue of propagation of these bound states by solving, numerically, the spatio-temporal Equation (6). To attempt such a numerical experiment, we have to ensure that the equation is mathematically well-posed (i.e. the solution exists, is unique and depends continuously on the initial data $V_i,i=1,2,3$ ). We remark that the nerve impulse lasts for a finite time T and the length, L, of the axon is also finite. Consequently the time and the space domains will be considered as bounded intervals.

3. Mathematical Analysis of the Model

In this section, we state and prove conditions under which an initial value problem of the form

$\frac{\partial V}{\partial t}=f\left(x,t\right)\frac{{\partial }^{2}V}{\partial x^2}+g\left(x,t\right)V\text{in}\left(0,L\right)\times \left[0,T\right]$ (10)

$V\left(x,0\right)=V_0\left(x\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}x\in \left[0,L\right],t=0$ (11)

with homogenous boundary conditions $V\left(0,t\right)=V\left(L,t\right)=0$ will have a unique solution. Non-homogeneous boundary conditions can be reduced to homogenous ones by homogenization depending on their smoothness.

3.1. Sobolev Spaces of Solutions

We now introduce some of the function spaces that form the basis of the mathematical framework for the analysis of an initial value problem of the form (10-11) [23] .

1) Given an interval I and the Hilbert space X, $C^k\left(I\mathrm{,}X\right)$ will denote the space of bounded k-continuously differentiable functions of the form $t\mapsto u\left(\cdot \mathrm{,}t\right)\in X$ equipped with the norm

$\Vert u\Vert =\underset{t\in I\mathrm{,}\left|\alpha \right|\le k}{\sup }{\Vert {\partial }^{\alpha }u\left(t\right)\Vert }_X\mathrm{.}$

For example the space $C^k\left(\left[\mathrm{0,}T\right]\mathrm{,}{L}^2\left(\mathrm{0,}L\right)\right)$ is the space of bounded continuous functions of the form $t\mapsto u\left(\cdot \mathrm{,}t\right)\in L^2\left(\mathrm{0,}L\right)$ with the norm

$\Vert u\Vert =\underset{t\in \left[0,T\right],\left|\alpha \right|\le k}{\sup }{\left\{{\displaystyle {\int }_0^L}{\left|{\partial }^{\alpha }u\left(x,t\right)\right|}^2\text{d}x\right\}}^{\frac{1}{2}}.$

2) The space $H^1\left(\mathrm{0,}L\right)$ will denote the space of measurable functions u such that $u\in L^2\left(\mathrm{0,}L\right)$ and $\frac{\text{d}u}{\text{d}x}\in L^2\left(\mathrm{0,}L\right)$ with the norm

${\Vert u\Vert }_{H^1\left(0,L\right)}={\left\{{\displaystyle {\int }_0^L}\left({\left|\frac{\text{d}u}{\text{d}x}\right|}^2+{\left|u\right|}^2\right)\text{d}x\right\}}^{\frac{1}{2}}$

3)The space $H_0^1\left(0,L\right)=\left\{u\in H^1\left(0,L\right):u\left(L\right)=u\left(0\right)=0\right\}$ equipped with the norm ${\Vert \cdot \Vert }_{H^1\left(0,L\right)}$ . It is also the closure of the space $\mathcal{D}\left(\mathrm{0,}L\right)$ of infinitely continuously differentiable functions with compact support in $\left(\mathrm{0,}L\right)$ .

4) The space $H^{-1}\left(\mathrm{0,}L\right)$ is the dual space of $H_0^1\left(\mathrm{0,}L\right)$ in the sense of distributions.

5) The space $L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ is the completion of $C\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ with respect to the norm

${\Vert u\Vert }_{L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)}={\left({\displaystyle {\int }_0^T}\left({\displaystyle {\int }_0^L}{\left|u\left(x\mathrm{,}t\right)\right|}^2+{\left|\frac{\partial u}{\partial x}\left(x\mathrm{,}t\right)\right|}^2\text{d}x\right)\text{d}t\right)}^{\frac{1}{2}}\mathrm{.}$

6) The space $H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$ with the norm

${\Vert u\Vert }_{H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)}={\left({\displaystyle {\int }_0^T}\left({\Vert u\Vert }_{H^{-1}\left(\mathrm{0,}L\right)}^2+{\Vert \frac{\partial u}{\partial t}\Vert }_{H^{-1}\left(\mathrm{0,}L\right)}^2\right)\text{d}t\right)}^{\frac{1}{2}}\mathrm{,}$

where

${\Vert u\Vert }_{H^{-1}\left(\mathrm{0,}L\right)}=\underset{v\in H_0^1\left(\mathrm{0,}L\right)}{\sup }\left(\frac{\left|u\left(v\right)\right|}{{\Vert v\Vert }_{H^1\left(\mathrm{0,}L\right)}}\right)$

7) The space $\mathcal{D}\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\Omega \right)\right)$ of infinitely continuously differentiable functions from $\left(\mathrm{0,}T\right)$ to $H_0^1\left(\Omega \right)$ which have a compact support on $\left(\mathrm{0,}T\right)$ .

3.2. Existence and Uniqueness of Solutions

Let us consider the operator $A\left(t\right)(\cdot )$ defined by

$A\left(t\right)V\left(x\mathrm{,}t\right)=f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}V}{\partial x^2}\left(x\mathrm{,}t\right)+g\left(x\mathrm{,}t\right)V\left(x\mathrm{,}t\right)\mathrm{.}$

The system (10-11) becomes

$\frac{\partial V}{\partial t}=A\left(t\right)V\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{in}\left(\mathrm{0,}L\right)\times \left[\mathrm{0,}T\right]$ (12)

$V\left(x\mathrm{,0}\right)=V_0\left(x\right)$ (13)

$V\left(0,t\right)=V\left(L,t\right)=0.$ (14)

Lemma 1. Define

$a\left(t,u,v\right)=-\left(A\left(t\right),u,v\right)=-{\displaystyle {\int }_0^L}A\left(t\right)uv\text{d}x$

on $ℝ\times H_0^1\left(\mathrm{0,}L\right)\times H_0^1\left(\mathrm{0,}L\right)$ . Then $a\left(t,u,v\right)$ satisfies the coercivity condition

$a\left(t\mathrm{,}v\mathrm{,}v\right)\ge C_1{\Vert v\Vert }_{H^1\left(\mathrm{0,}L\right)}^2-C_2{\Vert v\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\mathrm{,}$ (15)

where $C_1\mathrm{,}{C}_2$ are positive constants.

Proof. Let $v\left(\cdot \mathrm{,}t\right)\in H_0^1\left(\mathrm{0,}L\right)$ . Since $T<\infty$ and $L<\infty$ we see that f and g are positive and bounded (as continuous functions on bounded domains). Then there exists $M_1>0,M_2>0$ such that $M_1\le f\left(x\mathrm{,}t\right)\le M_2$ and $M_1\le g\left(x\mathrm{,}t\right)\le M_2$ for any $\left(x\mathrm{,}t\right)\in \left[\mathrm{0,}L\right]\times \left[\mathrm{0,}T\right]$ . We have that

$a\left(t,v,v\right)=-{\displaystyle {\int }_0^L}f\left(x,t\right)\frac{{\text{d}}^{2}v}{\text{d}{x}^2}v-g\left(x,t\right)v^2\text{d}x$ (16)

$\ge M_2{\displaystyle {\int }_0^L}\left(-\frac{{\text{d}}^{2}v}{\text{d}{x}^2}v-v^2\right)\text{d}x$ (17)

$\ge M_2\left({\displaystyle {\int }_0^L}\frac{\text{d}v}{\text{d}x}\frac{\text{d}v}{\text{d}x}-v^2\text{d}x-\left(v\left(L,t\right)-v\left(0,t\right)\right)\right)$ (18)

$\ge M_2{\displaystyle {\int }_0^L}{\left|\frac{\text{d}v}{\text{d}x}\right|}^2\text{d}x-M_2{\displaystyle {\int }_0^L}{\left|v\right|}^2\text{d}x.$ (19)

From the Poincare inequality,

${\displaystyle {\int }_0^L}{\left|\bar{v}v\right|}^2\text{d}x\ge C{\Vert v\Vert }_{H^1(\; 0,\; L\; )}$

where C is a positive constant. Consequently

$a\left(t\mathrm{,}v\mathrm{,}v\right)\ge C_1{\Vert v\Vert }_{H^1\left(\mathrm{0,}L\right)}-C_2{\Vert v\Vert }_{L^2\left(\mathrm{0,}L\right)}^2$

where $C_1=M_2{C}^2$ and $C_2=M_2$ . $\square$

To continue our way to the existence and uniqueness, we need to establish a relation between the space of solutions and the space of continuous functions.

Lemma 2. Suppose $v\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)\cap H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$ , then $v\in C\left(\left[\mathrm{0,}T\right]\mathrm{,}{L}^2\left(\mathrm{0,}L\right)\right)$ .

Proof

Let $v\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)\cap H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$ , $t\mathrm{,}{t}^{\mathrm{<mo>\; *\; </mo>}}\in ℝ$ then

${\displaystyle {\int }_{t^{*}}^t}\left({\displaystyle {\int }_0^L}\frac{\partial v}{\partial s}\left(x,s\right)v\left(x,s\right)\text{d}x\right)\text{d}s={\displaystyle {\int }_{t^{*}}^t}\left({\displaystyle {\int }_0^L}\frac{1}{2}\frac{\partial v^2}{\partial s}\left(x,s\right)\text{d}x\right)\text{d}s$

$=\frac{1}{2}{\displaystyle {\int }_{t^{*}}^t}\frac{\text{d}}{\text{d}s}\left({\displaystyle {\int }_0^L}{v}^2\left(x,s\right)\text{d}x\right)\text{d}s$ (20)

$=\frac{1}{2}{\displaystyle {\int }_{t^{*}}^t}\frac{\text{d}}{\text{d}s}\left({\Vert v\left(\cdot ,s\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\right)\text{d}s$ (21)

$=\frac{1}{2}\left({\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2-{\Vert v\left(\cdot ,t^{*}\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}\right).$ (22)

Consequently

${\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2={\Vert v\left(\cdot ,t^{*}\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2+2{\displaystyle {\int }_{t^{\mathrm{<mo>\; *\; </mo>}}}^t}\left({\displaystyle {\int }_0^L}\frac{\partial v}{\partial s}v\text{d}x\right)\text{d}s\mathrm{.}$

So if we choose $t^{\mathrm{<mo>\; *\; </mo>}}$ in such a way that ${\Vert v\left(\cdot ,t^{*}\right)\Vert }^2$ is the mean value of ${\Vert v\left(\cdot ,t\right)\Vert }^2$ in $\left[\mathrm{0,}T\right]$ , we have

$\begin{array}{c}{\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\text{d}t=\frac{1}{T}{\displaystyle {\int }_0^T}{\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\text{d}t+2{\displaystyle {\int }_{t*}^t}{\displaystyle {\int }_0^L}\frac{\partial v}{\partial s}v\text{d}x\text{d}s\\ \le \frac{1}{T}{\displaystyle {\int }_0^T}{\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\text{d}t+2{\displaystyle {\int }_0^T}{\Vert \frac{\partial v}{\partial s}\left(\cdot ,s\right)\Vert }_{H^{-1}\left(\Omega \right)}{\Vert v\left(\cdot ,s\right)\Vert }_{H^1\left(0,L\right)}\text{d}s\\ \le \frac{1}{T}{\Vert v\Vert }_{L^2\left(\left(0,T\right),L^2\left(0,L\right)\right)}+2{\Vert v\Vert }_{H^1\left(\left(0,T\right),H^{-1}\left(0,L\right)\right)}{\Vert v\Vert }_{L^2\left(\left(0,T\right),H^1\left(0,L\right)\right)}.\end{array}$

Then

$\begin{array}{c}{\Vert v\Vert }_{C\left(\left[0,T\right],L^2\left(0,L\right)\right)}=\underset{t\in \left[0,T\right]}{\max }{\Vert v\left(\cdot ,t\right)\Vert }_{L^2\left(0,L\right)}\\ \le \frac{1}{T}{\Vert v\Vert }_{L^2\left(\left(0,T\right),L^2\left(0,L\right)\right)}+2{\Vert v\Vert }_{H^1\left(\left(0,T\right),H^{-1}\left(0,L\right)\right)}{\Vert v\Vert }_{L^2\left(\left(0,T\right),H_0^1\left(0,L\right)\right)}\\ <\infty .\end{array}$

Hence

$v\in C\left(\left[\mathrm{0,}T\right]\mathrm{,}{L}^2\left(\mathrm{0,}L\right)\right)\mathrm{.}$

We can now prove the existence and uniqueness of solutions of problem (10-11).

Theorem 1. Assume that the function

$f\in L^2\left(\left(0,T\right),H^{-1}\left(\Omega \right)\right)$ and $V_0\in L^2\left(0,L\right)$

are given. Then (10-11) has a unique solution

$V\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)\cap H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^1\left(\mathrm{0,}L\right)\right)\mathrm{.}$

Proof.

Set $V=u{\text{e}}^{C_{2}t}$ where $C_2$ is the constant defined in inequality (15). Then

$\frac{\partial V}{\partial t}=\left(\frac{\partial u}{\partial t}+C_{2}u\right){\text{e}}^{C_{2}t}$

and the Equation (10) becomes

$\frac{\partial u}{\partial t}=f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}u}{\partial x^2}+\left(g\left(x\mathrm{,}t\right)-C_2\right)u\mathrm{.}$

Hence, the system (10-11) is equivalent to

$\frac{\partial u}{\partial t}=f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}u}{\partial x^2}+\left(g\left(x\mathrm{,}t\right)-C_2\right)u$ (23)

$u\left(x,0\right)=u_0\left(x\right)=V_0\left(x\right)$ (24)

$u\left(0,t\right)=u\left(L,t\right)=0$ (25)

We will show that (23-25) has a unique solution and conclude the existence and uniqueness of the solutions of (10-11). Let us set

$b\left(t,u,v\right)=-{\displaystyle {\int }_0^L}f\left(x,t\right)\frac{{\partial }^{2}u}{\partial x^2}v+\left(g\left(x,t\right)-C_2\right)uv\text{d}x.$

Then from the proof of Lemma 1, $g\left(x\mathrm{,}t\right)\le C_2$ and so

$-{\displaystyle {\int }_0^L}\left(g\left(x\mathrm{,}t\right)-C_2\right)u^2\text{d}x\ge 0.$

Consequently, from the coercivity condition (15), Poincare inequality and integration by parts,

$b\left(t\mathrm{,}u\mathrm{,}u\right)\ge -{\displaystyle {\int }_0^L}f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}u}{\partial x^2}u\text{d}x\ge C{\Vert u\left(\cdot \mathrm{,}t\right)\Vert }_{H^1\left(\mathrm{0,}L\right)}^2\mathrm{.}$ (26)

Proof of uniqueness

Let u be a solution of (23-25) then we have

${\displaystyle {\int }_0^L}\frac{\partial u}{\partial t}u\text{d}x=-b\left(t\mathrm{,}u\mathrm{,}u\right)$

and

${\displaystyle {\int }_0^T}{\displaystyle {\int }_0^L}\frac{\partial u}{\partial t}u\text{d}x\text{d}t=\frac{1}{2}\left({\Vert u\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2-{\Vert u_0(\cdot )\Vert }_{L^2\left(\mathrm{0,}L\right)}^2\right).$

Consequently, using (26)

$\frac{1}{2}{\Vert u\left(\cdot ,t\right)\Vert }_{L^2\left(\mathrm{0,}L\right)}^2+C{\Vert u\left(\cdot ,t\right)\Vert }_{H^1\left(\mathrm{0,}L\right)}^2\le \frac{1}{2}{\Vert u_0\Vert }_{H^1\left(\mathrm{0,}L\right)}^2$

and

${\Vert u\Vert }_{L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^1\left(\mathrm{0,}L\right)\right)}^2\le \frac{1}{2C}{\Vert u_0\Vert }_{H^1\left(\mathrm{0,}L\right)}^2\le C{\Vert u_0(\cdot )\Vert }_{L^2\left(\mathrm{0,}L\right)}^2$

since $H^1\left(\mathrm{0,}L\right)$ is compactly embedded in $L^2\left(\mathrm{0,}L\right)$ . Therefore,

${\Vert u\Vert }_{L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^1\left(\mathrm{0,}L\right)\right)}\le C{\Vert u_0\Vert }_{L^2\left(\mathrm{0,}L\right)}\mathrm{.}$

So if $u_1$ and $u_2$ are two solutions of (23) then

${\Vert u_1-u_2\Vert }_{L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)}\le 0$

then $u_1=u_2$ .

Proof of existence

$H_0^1\left(\mathrm{0,}L\right)$ is separable and so has a countable dense subset ${\left\{{\varphi }_n\right\}}_{n\in \mathbb{N}}$ . From the Gram-Schmidt orthogonalization process we can assume that the $\left\{{\varphi }_n\right\}$ are linearly independent such that

$\overline{\text{Span}\left\{{\varphi }_n\mathrm{<mo>\; :\; </mo>}n\in \mathbb{N}\right\}}=H_0^1\left(\mathrm{0,}L\right)\mathrm{.}$

Let ${\Pi }_n$ be the orthogonal projection from $L^2\left(\mathrm{0,}L\right)$ on to

$\text{Span}\left\{{\varphi }_i\mathrm{,1}\le i\le n\right\}$

and let

$u_n\left(.,t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\alpha }_i\left(t\right){\varphi }_i(\; .\; )$

be the solution of

${\displaystyle {\int }_0^L}\frac{\partial u_n}{\partial t}{\varphi }_i\text{d}x=-b\left(t,u_n,{\varphi }_i\right),i=1,\cdots ,n$ (27)

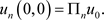
The system (27) is a system of linear ODEs for the coefficients ${\alpha }_i\left(t\right)$ and so has a unique solution as a consequence of Picard-Lindelof Theorem [23] .

Using a similar proof as in Lemma 1 one has

${\Vert u_n\left(.,T\right)\Vert }_{L^2\left(0,T\right)}^2-{\Vert {\Pi }_n{u}_0\Vert }_{L^2\left(0,T\right)}^2=-2{\displaystyle {\int }_0^T}b\left(t,u_n,u_n\right)\text{d}t$

and

${\Vert u_n\Vert }_{L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)}\le C{\Vert {\Pi }_n{u}_0\Vert }_{L^2\left(\mathrm{0,}T\right)}\le C{\Vert u_0\Vert }_{L^2\left(\mathrm{0,}T\right)}$ (28)

since (by the linearity and continuity of ${\Pi }_n$ , ${\Vert {\Pi }_n{u}_0\Vert }_{L^2\left(\mathrm{0,}T\right)}\le {\Vert u_0\Vert }_{L^2\left(\mathrm{0,}T\right)}$ ). Then $\left\{u_n\right\}$ is bounded in $L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ and consequently has a subsequence still denoted ${\left\{u_n\right\}}_n$ that converges weakly in $L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ to a limit u. Let $\varphi \in \mathcal{D}\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\Omega \right)\right)$ be of the form

$\varphi \left(t\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}}{\beta }_i\left(t\right){\varphi }_i$ (29)

for some $N\in \mathbb{N}$ where ${\beta }_i\in \mathcal{D}\left(\left(\mathrm{0,}T\right)\mathrm{,}ℝ\right)$ . For $n\ge N$ , one has

${\displaystyle {\int }_0^L}\frac{\partial u_n}{\partial t}\varphi \text{d}x=-b\left(t\mathrm{,}{u}_n\mathrm{,}\varphi \right)$

so

${\displaystyle {\int }_0^T}{\displaystyle {\int }_0^L}\frac{\partial u_n}{\partial t}\varphi \text{d}x\text{d}t=-{\displaystyle {\int }_0^T}b\left(t\mathrm{,}{u}_n\mathrm{,}\varphi \right)\text{d}t\mathrm{.}$

Taking the limit one has

${\displaystyle {\int }_0^T}\left({\displaystyle {\int }_0^L}\frac{\partial u}{\partial t}\varphi \text{d}x\right)\text{d}t=-{\displaystyle {\int }_0^T}b\left(t\mathrm{,}u\mathrm{,}\varphi \right)\text{d}t\mathrm{.}$ (30)

Since the functions $\varphi$ are dense in $\mathcal{D}\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ , (30) holds in the sense of distributions. This implies

$\frac{\partial u}{\partial t}=f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}u}{\partial x^2}+\left(g\left(x\mathrm{,}t\right)-c_2\right)u\mathrm{.}$

From (30) we can also see that $\frac{\partial u}{\partial t}\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$ . Hence $u\in H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$ and $u\in C\left(\left(\mathrm{0,}T\right)\mathrm{,}{L}^2\left(\mathrm{0,}L\right)\right)$ from Lemma 1.

Let us now prove that $u\left(\cdot \mathrm{,0}\right)=u_0$ . Let $\varphi \in H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ such that $\varphi \left(T\right)=0$ . Functions of the form (29) are dense in $H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)$ . So if $\varphi$ has the form (29) and $n\ge N$ , one has in (27) (using integration by parts over t)

$-{\displaystyle {\int }_0^T}\left({\displaystyle {\int }_0^L}{u}_n\frac{\partial \varphi }{\partial t}\text{d}x\right)\text{d}t+{\displaystyle {\int }_0^L}{u}_n\left(\cdot ,0\right)\varphi \left(0\right)\text{d}x=-{\displaystyle {\int }_0^T}b\left(t,u_n,\varphi \right)\text{d}t.$

Taking the limit, one has

$-{\displaystyle {\int }_0^T}\left({\displaystyle {\int }_0^L}u\left(\cdot ,t\right)\frac{\partial \varphi }{\partial t}\left(\cdot ,t\right)\text{d}x\right)\text{d}t+{\displaystyle {\int }_0^L}u\left(\cdot ,0\right)\varphi \left(\cdot ,0\right)\text{d}x=-{\displaystyle {\int }_0^T}b\left(t,u,\varphi \right)\text{d}t.$ (31)

Multiplying (23) by $\varphi$ and taking the integral over $\left(\mathrm{0,}T\right)$ yields

${\displaystyle {\int }_0^T}\left({\displaystyle {\int }_0^L}u\left(\cdot ,t\right)\frac{\partial \varphi }{\partial t}\left(\cdot ,t\right)\text{d}x\right)\text{d}t+{\displaystyle {\int }_0^L}{u}_0(\cdot )\varphi \left(\cdot ,0\right)\text{d}x=-{\displaystyle {\int }_0^T}b\left(t,u,\varphi \right)\text{d}t.$ (32)

Equations (31) and (32) imply that $u_0=u\left(0\right)$ . $\square$

Remark. Considering the model (6), we observe that the function

$f\left(x\mathrm{,}t\right)=\frac{2D}{1+\tanh \left(x-4t\right)}\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)$

and each of the bound states

$V_i\in L^2\left(\mathrm{0,}L\right)\mathrm{,}i=\mathrm{1,2,3.}$

Hence, by Theorem 1, the initial value problem (6) has a unique solution

$V\in L^2\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}_0^1\left(\mathrm{0,}L\right)\right)\cap H^1\left(\left(\mathrm{0,}T\right)\mathrm{,}{H}^{-1}\left(\mathrm{0,}L\right)\right)\mathrm{.}$

4. Numerical Experiments

This section investigates numerically the behavior of the model (6) using the bound states $V_i,i=1,2,3$ in (7-9) as the initial states of the system, the two points boundary value problem is

$\frac{\partial V}{\partial t}-\frac{2D}{1+\tanh \left(x-4t\right)}\frac{{\partial }^{2}V}{\partial x^2}-\frac{4\epsilon {\text{sech}}^2\left(x-4t\right)}{1+\tanh \left(x-4t\right)}V=0,\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{in}\left(0,L\right)\times \left[0,T\right]$ (33)

$V\left(x\mathrm{,0}\right)=V_i\left(x\right)\mathrm{,}$ (34)

$V\left(0,t\right)=V_i\left(0-4t\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}V\left(L,t\right)=V_i\left(L-4t\right)$ (35)

The smoothness of the domain and the data allow us to use the Forward and Backward Euler Finite difference methods.

The Finite Difference Method (FDM) aims at approximating straight forwardly the value of the solution of a given problem at a chosen set of discrete points of the domain. Suppose $\left[\mathrm{0,}L\right]$ is partitionned into $N_x$ subintervals $\left(x_{k-1}\mathrm{,}{x}_k\right)$ , $k=1,\cdots ,N_x$ of length $h=L/N_x$ with $0=x_0<x_1<\cdots <x_{N_x}=L$ and similarly $\left[\mathrm{0,}T\right]$ is partitionned into $N_t$ subintervals $\left(t_{j-1}\mathrm{,}{t}_j\right)$ , $j=1,\cdots ,N_t$ of length $\tau =T/N_x$ with $0=t_0<t_1<\cdots <t_{N_t}=T$ . Thus $\left[\mathrm{0,}L\right]\times \left[\mathrm{0,}T\right]$ is approximated by the set of points $\bar{G}=\left\{\left(x_k,t_j\right),0\le k\le N_x,\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; 0}\le j\le N_t\right\}$ , $\left(x_k\mathrm{,}{t}_j\right)=\left(kh\mathrm{,}j\tau \right)$ .

4.1. The Forward Euler Finite Difference Method

Setting $f\left(x\mathrm{,}t\right)=\frac{2D}{1+\tanh \left(x-4t\right)}$ and $g\left(x,t\right)=\frac{4\epsilon {\text{sech}}^2\left(x-4t\right)}{1+\tanh \left(x-4t\right)}$ , $V\left(x_k\mathrm{,}{t}_j\right)=V_k^j$ , using the difference quotients $\frac{\partial V}{\partial t}\left(x_k\mathrm{,}{t}_j\right)\approx \frac{V\left(x_k\mathrm{,}{t}_j+\tau \right)-V\left(x_k\mathrm{,}{t}_j\right)}{\tau }+\mathcal{O}\left(\tau \right)=\frac{V_k^{j+1}-V_k^j}{\tau }+\mathcal{O}\left(\tau \right)$ and $\begin{array}{c}\frac{{\partial }^{2}V}{\partial x^2}\approx \frac{V\left(x_k-h,t_j\right)-2V\left(x_k,t_j\right)+V\left(x_k+h,t_j\right)}{h^2}+\mathcal{O}\left(h^2\right)\\ =\frac{V_{k-1}^j-2V_k^j+V_{k+1}^j}{h^2}+\mathcal{O}\left(h^2\right)\end{array}$ , Problem (33-35) can be approximated by the discrete Problem

$\begin{array}{l}{V}_k^{j+1}=\frac{\tau }{h^2}f\left(x_k,t_j\right)V_{k-1}^j+\left(1-2\frac{\tau }{h^2}f\left(x_k,t_j\right)+\tau g\left(x_k,t_j\right)\right)V_k^j\\ +\frac{\tau }{h^2}f\left(x_k,t_j\right)V_{k+1}^j,j\ge 1,1\le k<N_x\\ V_k^0=V_i\left(x_k\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}k=0,\cdots ,N_x\\ V_0^j=V_i\left(0-4t_j\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{V}_{N_x}^j=V_i\left(L-4t_j\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j=0,\cdots ,N_t.\end{array}$ (36)

The convergence and accuracy of the method require its stability and consistency. The stability is proved in the subsequent lemmas.

Lemma 3. Let U and V be arbitrarily discrete functions defined on G. Define $\Vert U\Vert =\underset{k=0,\cdots ,N_x}{\max }\left|U\left(x_k,t\right)\right|$ . If ${\Vert U\Vert }^{t+\tau }\le \tau {\Vert V\Vert }^t+{\Vert U\Vert }^t$ for any $t=j\tau$ , $j=0,\cdots ,N_t$ , then

${\Vert U\Vert }^t\le {\displaystyle {\int }_0^t}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0\mathrm{.}$

Proof. The proof is done by induction on j. For $j=0$ , ${\Vert U\Vert }^0\le {\displaystyle {\int }_0^0}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0$ .

Suppose for $j\ge 0$ fixed, ${\Vert U\Vert }^{j\tau }\le {\displaystyle {\int }_0^{j\tau }}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0$ . Let us show that

$\begin{array}{c}\left({\displaystyle {\int }_0^{\left(j+1\right)\tau }}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0\right)={\displaystyle {\int }_{j\tau }^{\left(j+1\right)\tau }}{\Vert V\Vert }^s\text{d}s+{\displaystyle {\int }_0^{j\tau }}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0\\ \ge {\displaystyle {\int }_{j\tau }^{\left(j+1\right)\tau }}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^{j\tau }\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{by}\text{induction}\text{Hypothesis}\\ \ge \tau {\Vert V\Vert }^{j\tau }+{\Vert U\Vert }^{j\tau }\\ \ge {\Vert U\Vert }^{\left(j+1\right)\tau }\end{array}$

Hence by induction, for any $t=j\tau$ , $j=0,\cdots ,N_t$ , ${\Vert U\Vert }^t\le {\displaystyle {\int }_0^t}{\Vert V\Vert }^s\text{d}s+{\Vert U\Vert }^0$ .

Define the operator

$\begin{array}{c}{L}_{\tau h}W=\frac{1}{\tau }(W\left(x,t+\tau \right)-\left(1-2\lambda f\left(x,t\right)+\tau g\left(x,t\right)\right)W\left(x,t\right)\\ -\lambda f\left(x,t\right)W\left(x+h,t\right)-\lambda f\left(x,t\right)W\left(x-h,t\right))\end{array}$

where $\lambda =\frac{\tau }{h^2}$ .

The first Equation (33) can be written in the form $L_{\tau h}V=0$ in G. It follows using the existence and uniqueness of the solution that $L_{\tau h}$ is invertible. Knowing that the fuctions f and g are smooth and bounded, we assume the following conditions for stability.

$f\left(x\mathrm{,}t\right)\ge 0\text{for}\text{any}0\le x\le L\mathrm{,\; <mtext>\; \hspace{0.17em}\; </mtext>\; 0}\le t\le T$ (37)

$\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; 1}-2\lambda f\left(x\mathrm{,}t\right)+\tau g\left(x\mathrm{,}t\right)\ge 0$ (38)

The step size $\tau$ is suffciently small so that

$\tau g\left(x\mathrm{,}t\right)\approx 0$ . (39)

Based on Assumptions (37-39), the following Lemma holds.

Lemma 4. Suppose that Assumptions (37-39) hold and consider the operator $A_{\tau h}=\left(L_{\tau h}\mathrm{,}Id\right)$ where Id is the identity operator from ${\mathcal{C}}^1\left(G\right)$ to ${\mathcal{C}}^1\left(G\right)$ . There exist $C>0$ such that $\Vert A_{\tau h}^{-1}\Vert \le C$ .

Proof. Let V be in ${\mathcal{C}}^1\left(G\right)$ , using the definition of $L_{\tau h}$ one has

$\begin{array}{c}\left|V\left(x\mathrm{,}t+\tau \right)\right|=|\tau L_{\tau h}V+\left(1-2\lambda f\left(x\mathrm{,}t\right)+\tau g\left(x\mathrm{,}t\right)\right)V\left(x\mathrm{,}t\right)\\ +\lambda f\left(x\mathrm{,}t\right)V\left(x+h\mathrm{,}t\right)+\lambda f\left(x\mathrm{,}t\right)V\left(x-h\mathrm{,}t\right)|\end{array}$

$\begin{array}{l}\le \tau \left|L_{\tau h}V\right|+\left(1-2\lambda f\left(x\mathrm{,}t\right)+\tau g\left(x\mathrm{,}t\right)\right)\left|V\left(x\mathrm{,}t\right)\right|\\ +\lambda f\left(x\mathrm{,}t\right)\left|V\left(x+h\mathrm{,}t\right)\right|+\lambda f\left(x\mathrm{,}t\right)\left|V\left(x-h\mathrm{,}t\right)\right|\end{array}$

$\begin{array}{l}\le \tau {\Vert L_{\tau h}V\Vert }^t+\left(1-2\lambda f\left(x\mathrm{,}t\right)+\tau g\left(x\mathrm{,}t\right)\right){\Vert V\Vert }^t\\ +2\lambda f\left(x\mathrm{,}t\right){\Vert V\Vert }^t\end{array}$ from Assumptions (37-38)

$\le \tau {\Vert L_{\tau h}V\Vert }^t+\left(1+\tau g\left(x\mathrm{,}t\right)\right){\Vert V\Vert }^t$

$\approx \tau {\Vert L_{\tau h}V\Vert }^t+{\Vert V\Vert }^t$ from Assumption (39)

Hence ${\Vert V\Vert }^{t+\tau }\le \tau {\Vert L_{\tau h}V\Vert }^t+{\Vert V\Vert }^t$ and we can apply Lemma 3 to see that

$\begin{array}{c}{\Vert V\Vert }^t\le {\displaystyle {\int }_0^t}{\Vert L_{\tau h}V\Vert }^s\text{d}s+{\Vert V\Vert }^0\\ \le t{\Vert L_{\tau h}V\Vert }^t+{\Vert V\Vert }^0\\ \le \max \left\{\mathrm{1,}T\right\}\left({\Vert L_{\tau h}V\Vert }^t+{\Vert V\Vert }^0\right)\\ \le C{\Vert A_{\tau h}V\Vert }^t\mathrm{,\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}C\mathrm{<mo>\; =\; </mo>}\max \left\{\mathrm{1,}T\right\}\end{array}$

Hence $\Vert A_{\tau h}^{-1}\Vert \le C$ .

Lemma 4 shows that the sequence ${\left\{A_{\tau h}^{-1}\right\}}_{\tau \mathrm{,}h}$ is uniformly bounded, consequently the FDM is stable. It remains to show that the FDM is consistent. We can see from the Taylor’s formula that for any function V twice differentiable with respect to x and differentiable with respect to t

$\left|L_{\tau h}V-\left(\frac{\partial V}{\partial t}-f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}V}{\partial x^2}-g\left(x\mathrm{,}t\right)V\right)\right|=\mathcal{O}\left(\tau +h^2\right)\mathrm{.}$

We have the following convergence theorem.

Theorem 2. Let V be the solution of (33-35) and W be the solution of (36). Then ${\Vert W-V\Vert }^T\to 0$ as $h\to 0$ and $\tau \to 0$ .

Proof. From Lemma 3 one has

$\begin{array}{c}{\Vert W-V\Vert }^T\le T{\Vert L_{\tau h}\left(W-V\right)\Vert }^T+{\Vert W-V\Vert }^0\\ \le T{\Vert L_{\tau h}\left(W-V\right)\Vert }^T\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{since}W=V\text{at}t=0\\ \le T{\Vert L_{\tau h}W-L_{\tau h}V\Vert }^T\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{since}W=V\text{at}t=0\\ \le T{\left|\left|\left(\frac{\partial V}{\partial t}-f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}V}{\partial x^2}-g\left(x\mathrm{,}t\right)V\right)-L_{\tau h}V\right|\right|}^T\\ \le C\left(\tau +h^2\right)\mathrm{.}\end{array}$

The Forward Euler FDM is consistent of order 1 and stable with the stability conditions (37 - 39). The stability and consistency imply the convergence of the FDM with an accuracy $\mathcal{O}\left(\tau +h^2\right)$ .

4.2. The Backward Euler Finite Difference Method

Setting $f\left(x\mathrm{,}t\right)=\frac{2D}{1+\tanh \left(x-4t\right)}$ and $g\left(x\mathrm{,}t\right)=\frac{4\epsilon {\text{sech}}^2\left(x-4t\right)}{1+\tanh \left(x-4t\right)}$ , $V\left(x_k\mathrm{,}{t}_j\right)=V_k^j$ , using the difference quotients $\frac{\partial V}{\partial t}\left(x_k,t_j\right)\approx \frac{V\left(x_k,t_j+\tau \right)-V\left(x_k,t_j\right)}{\tau }+\mathcal{O}\left(\tau \right)=\frac{V_k^{j+1}-V_k^j}{\tau }+\mathcal{O}\left(\tau \right)$ and $\begin{array}{c}\frac{{\partial }^{2}V}{\partial x^2}\approx \frac{V\left(x_k-h,t_j+\tau \right)-2V\left(x_k,t_j+\tau \right)+V\left(x_k+h,t_j+\tau \right)}{h^2}+\mathcal{O}\left(h^2\right)\\ =\frac{V_{k-1}^{j+1}-2V_k^{j+1}+V_{k+1}^{j+1}}{h^2}+\mathcal{O}\left(h^2\right)\end{array}$ , problem (33-35) can be approximated by the discrete Problem

$\begin{array}{l}{V}_k^j=-\frac{\tau }{h^2}f\left(x_k,t_{j+1}\right)V_{k-1}^{j+1}+\left(1+2\frac{\tau }{h^2}f\left(x_k,t_{j+1}\right)-\tau g\left(x_k,t_{j+1}\right)\right)V_k^{j+1}\\ -\frac{\tau }{h^2}f\left(x_k,t_{j+1}\right)V_{k+1}^{j+1},j\ge 1,1\le k<N_x\\ V_k^0=V_i\left(x_k\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}k=0,\cdots ,N_x\\ V_0^j=V_i\left(0-4t_j\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{V}_{N_x}^j=V_i\left(L-4t_j\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j=0,\cdots ,N_t.\end{array}$ (40)

As in the previous subsection, it will be shown that the Backward Euler FDM is stable and consistent then convergent. Define the operator

$\begin{array}{c}{L}_{\tau h}W=\frac{1}{\tau }(W\left(x,t\right)-\left(1+2\lambda f\left(x,t+\tau \right)-\tau g\left(x,t\right)\right)W\left(x,t+\tau \right)\\ \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}+\lambda f\left(x,t+\tau \right)W\left(x-h,t+\tau \right)+\lambda f\left(x,t+\tau \right)W\left(x+h,t+\tau \right))\end{array}$

where $\lambda =\frac{\tau }{h^2}$ . We suppose the following assumptions:

$f\left(x\mathrm{,}t\right)\ge 0\text{for}\text{any}0\le x\le L\mathrm{,\; <mtext>\; \hspace{0.17em}\; </mtext>\; 0}\le t\le T$ (41)

The step size $\tau$ is suffciently small so that

$\tau g\left(x\mathrm{,}t\right)\approx 0$ (42)

Based on these assumptions one uses the expression of 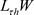to obtain

$\begin{array}{c}\left|W\left(x\mathrm{,}t\right)-\tau L_{\tau h}W\right|\ge \left(1+2\lambda f\left(x\mathrm{,}t\right)\right)\left|W\left(x\mathrm{,}t+\tau \right)\right|-\lambda f\left(x\mathrm{,}t\right)\left|W\left(x-h\mathrm{,}t+\tau \right)\right|\\ -\lambda f\left(x\mathrm{,}t\right)\left|W\left(x+h\mathrm{,}t+\tau \right)\right|\\ \ge \left(1+2\lambda f\left(x\mathrm{,}t\right)\right)\left|W\left(x\mathrm{,}t+\tau \right)\right|-2\lambda f\left(x\mathrm{,}t\right){\Vert W\Vert }^{t+\tau }\end{array}$

then $\left(1+2\lambda f\left(x\mathrm{,}t\right)\right)\left|W\left(x\mathrm{,}t+\tau \right)\right|\le 2\lambda f\left(x\mathrm{,}t\right){\Vert W\Vert }^{t+\tau }+{\Vert W-\tau L_{\tau h}W\Vert }^t$ .

Setting $M_t=\underset{x\in \omega }{\max }\left|f\left(x\mathrm{,}t\right)\right|$ , it follows that $\left(1+2\lambda M_t\right){\Vert W\Vert }^{t+\tau }\le 2\lambda M_t{\Vert W\Vert }^{t+\tau }+{\Vert W-\tau L_{\tau h}W\Vert }^t$ and then ${\Vert W\Vert }^{t+\tau }\le {\Vert W-\tau L_{\tau h}W\Vert }^t\le {\Vert W\Vert }^t+\tau {\Vert L_{\tau h}W\Vert }^t$ . Hence

$\begin{array}{c}{\Vert W\Vert }^t\le {\Vert W\Vert }^{t-\tau }+\tau {\Vert L_{\tau h}W\Vert }^{t-\tau }\le {\Vert W\Vert }^{t-\tau }+\tau {\Vert L_{\tau h}W\Vert }^t\\ \le {\Vert W\Vert }^{t-2\tau }+\tau {\Vert L_{\tau h}W\Vert }^{t-2\tau }+\tau {\Vert L_{\tau h}W\Vert }^t\\ \le {\Vert W\Vert }^{t-2\tau }+2\tau {\Vert L_{\tau h}W\Vert }^t\le \cdots \\ \le {\Vert W\Vert }^0+j\tau {\Vert L_{\tau h}W\Vert }^t={\Vert W\Vert }^0+t{\Vert L_{\tau h}W\Vert }^t\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{if}t=j\tau \\ \le \max \left\{\mathrm{1,}T\right\}\left({\Vert W\Vert }^0+{\Vert L_{\tau h}W\Vert }^t\right)\le C{\Vert A_{\tau h}W\Vert }^t\end{array}$

where $C=\max \left\{\mathrm{1,}T\right\}$ and $A_{\tau h}=\left(L_{\tau h}\mathrm{,}Id\right)$ . It can be concluded that ${\Vert A_{\tau h}^{-1}\Vert }^t\le C$ and that the sequence ${\left\{A_{\tau h}\right\}}_{hk}$ is uniformly bounded. Consequently the FDM is stable. One can still use the Taylor formula to show that the method is consistent of order $\mathcal{O}\left(\tau +h^2\right)$ . The following theorem show the convergence.

Theorem 3. Let V be the solution of (33-35) and W be the solution of (40). Then ${\Vert W-V\Vert }^T\to 0$ as $h\to 0$ and $\tau \to 0$ .

Proof.

$\begin{array}{c}{\Vert W-V\Vert }^T\le T{\Vert L_{\tau h}W-L_{\tau h}V\Vert }^T+{\Vert W-V\Vert }^0\\ \le T{\Vert L_{\tau h}W-L_{\tau h}V\Vert }^T\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{since}W=V\text{at}t=0\\ \le T{\left|\left|\left(\frac{\partial V}{\partial t}-f\left(x\mathrm{,}t\right)\frac{{\partial }^{2}V}{\partial x^2}-g\left(x\mathrm{,}t\right)V\right)-L_{\tau h}V\right|\right|}^T\\ \le C\left(\tau +h^2\right)\mathrm{.}\end{array}$

The Backward Euler FDM is consistent of order 1 $\left(\mathcal{O}\left(\tau +h^2\right)\right)$ and converges under the conditions (41-42).

4.3. Example 1

This example investigates numerically the behavior of the model (6) using the bound states $V_i,i=1,2,3$ in (33-35) as the initial states of the system for $\epsilon ={10}^{-13}$ . The stability conditions (37-42) are respected by the respective FDM used.

Table 1 and Table 2 present the error estimates for the Forward and the backward Euler FDM using the maximum error of two successive approximated solutions $V_{h_i}^{{\tau }_i}$ and 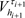of two successive refinements $\left({\tau }_i\mathrm{,}{h}_i\right)$ and $\left({\tau }_{i+1}\mathrm{,}{h}_{i+1}\right)$ using the formula

$\Vert V_{h_i}^{{\tau }_i}-V_{h_{i+1}}^{{\tau }_{i+1}}\Vert =\underset{\left(x_k,t_j\right)\in G}{\max }\left|V_{h_i}^{{\tau }_i}\left(x_k,t_j\right)-V_{h_{i+1}}^{{\tau }_{i+1}}\left(x_k,t_j\right)\right|,{\tau }_{i+1}=\frac{{\tau }_i}{2},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{h}_{i+1}=\frac{h_i}{2}.$

The consistency order $\alpha$ is computed using the formula

$\alpha ={\log }_2\left(\frac{\Vert V_{h_i}^{{\tau }_i}-V_{h_{i-1}}^{{\tau }_{i-1}}\Vert }{\Vert V_{h_i}^{{\tau }_i}-V_{h_{i+1}}^{{\tau }_{i+1}}\Vert }\right).$

The following figures are obtained for a space mesh spacing $h=2^{-3}$ and a time mesh spacing $\tau =\frac{h^2}{4}$ to respect the stability condition. Results in Figures 1-3 depicted below showing that the bound states do actually propagate in the x-t plane.

4.4. Example 2

We consider the same problem (33-35) with $\epsilon$ varying in the set $\left\{5\times {10}^{-3}\mathrm{,5}\times {10}^{-4}\mathrm{,5}\times {10}^{-5}\right\}$ using a backward Euler Finite difference method, the following figures are obtained for a space mesh spacing $h=2^{-6}$ and a time mesh spacing $\tau =h$ . Results in Figures 5-7 depicted below are still showing that the bound states do actually propagate in the x-t plane. Figure 4 shows the behaviour of the approximated solutions at $t=1/2$ .

Figure 1. Sketches of the first bound mode for the action potential, in the steady state and its evolution in the x-t plane.

Figure 2. Sketches of the second bound mode for the action potential, in the steady state and its evolution in the x-t plane.

Table 1. Error estimates of the Forward Euler FDM.

Table 2. Error estimates of the Backward Euler FDM.

Figure 3. Sketches of the third bound mode for the action potential, in the steady state and its evolution in the x-t plane.

Figure 4. Bound mode: V₁, Bound mode: V₂ Bound mode: V₃.

Figure 5. Bound mode: V₁, $\epsilon =5\times {10}^{-3}$ Bound mode: V₁, $\epsilon =5\times {10}^{-4}$ Bound mode: V₁, $\epsilon =5\times {10}^{-5}$ .

Figure 6. Bound mode: V₂, $\epsilon =5\times {10}^{-3}$ Bound mode: V₂, $\epsilon =5\times {10}^{-4}$ Bound mode: V₂, $\epsilon =5\times {10}^{-5}$ .

Figure 7. Bound mode: V₃, $\epsilon =5\times {10}^{-3}$ Bound mode: V₃, $\epsilon =5\times {10}^{-4}$ Bound mode: V₃, $\epsilon =5\times {10}^{-5}$ .

5. Conclusions

We have considered the hybrid model for nerve pulse generation and propagation proposed by Mengnjo, Dikandé and Ngwa. This model consists of a system of coupled partial differential equations. By considering the steady states of the system, we formulated an initial value problem that governs the evolution of the action potential. This is a linear parabolic equation with variable coefficients and an initial profile. To analyse the system, we formulated and proved, in general, the conditions under which such an initial value problem will have a unique solution and verified that the initial value problem governing the evolution of the action potential satisfies these conditions and hence has a unique solution. Due to the complex nature of the equation (variable coefficients in both independent variables), there are no known analytical techniques that can be used to solve the equation. Because of this difficulty we designed a numerical experiment to simulate the approximate solutions and thus gain insight in to their long term behaviour. The numerical experiments reveal that the solutions are bounded pulses propagating in the x-t plane with constant velocity and shape similar to that of the initial profile. We interpret this to mean that the initial profile which is a steady state solution to the MDN model evolves by translation without attenuation. This observation falls in line with what should be expected of a healthy nerve cell: Generate a pulse and propagate it without distortion.

In our model, we have combined both electrical and mechanical processes to generate the nerve pulse. We have demonstrated analytically that the propagation mechanism of the action potential is actually an interplay between the electrical and thermodynamic processes of the nerve cell. Considering the fact that the thermodynamic processes can be perturbed by both internal and external factors, we can subject our model to such factors and observe its behaviour. This opens up possible applications in the modelling of pathologies of nervous pathways. This could lead to a breakthrough in understanding some nervous disorders and more effective treatments designed. We thus see a major application of our work in the field of medicine.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Hodgkin, A.L. and Huxley, A.F. (1952) A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. The Journal of Physiology, 117, 500-544. https://doi.org/10.1113/jphysiol.1952.sp004764
[2]	Scott, A.C. (1975) The Electrophysics of a Nerve Fiber. Reviews of Modern Physics, 47, 487-553. https://doi.org/10.1103/RevModPhys.47.487
[3]	Fitzhugh, R. (1961) Impulses and Physiological States in Theoretical Models of the Nerve Membrane. Biophysical Journal, 1, 445-466. https://doi.org/10.1016/S0006-3495(61)86902-6
[4]	Nagumo, J., Arimoto, J.S. and Yoshizawa, S. (1962) An Active Pulse Transmission Line Simulating Nerve Axon. Proceedings of the IRE, 50, 2061-2070. https://doi.org/10.1109/JRPROC.1962.288235
[5]	Engelbretcht, J. (1981) On Theory of Pulse Transmission in a Nerve Fibre. Proceedings of the Royal Society of London, 375, 195-209. https://doi.org/10.1098/rspa.1981.0047
[6]	Tasaki, I. and Matsumoto. G. (2002) On the Cable Theory of Nerve Conduction. Bulletin of Mathematical Biology, 64, 1069-1082. https://doi.org/10.1006/bulm.2002.0310
[7]	Heimburg, T. and Jackson, A.D. (2005) On Soliton Propagation in Biomembranes and Nerves. PNAS, 102, 9790-9795. https://doi.org/10.1073/pnas.0503823102
[8]	Dikandé, A.M. and Ga-Akeku, B. (2008) Localized Short Impulses in a Nerve Model with Self-Excitable Membrane. Physical Review E, 80, Article ID: 041904. https://doi.org/10.1103/PhysRevE.80.041904
[9]	Keynes, R.D. and Aidley, D.J. (1982) Nerve and Muscle. Cambridge University Press, Cambridge.
[10]	Poznanski, R.R., Cacha, L.A., Al-Wesabi, Y.M.S., Ali, J., Bahadoran, M., Yupapin, P.P. and Yunus, J. (2017) Solitonic Conduction of Electronic Signals in Neuronal Branchlets with Polarized Microstructure. Scientific Reports, 7, Article No. 2746. https://doi.org/10.1038/s41598-017-01849-3
[11]	Fongang Achu, G., Moukam-Kakmeni, F.M. and Dikandé, A.M. (2018) Breathing Pulses in the Damped-Soliton Model for Nerves. Physical Review E, 97, Article ID: 012211. https://doi.org/10.1103/PhysRevE.97.012211
[12]	Warman, E.N., Grill, W.M. and Duran, D. (1992) Modeling the Effects of Electric Fields on Nerve Fibers: Determination of Excitation Thresholds. IEEE Transactions on Bio-Medical Electronics, 39, 1244-1254. https://doi.org/10.1109/10.184700
[13]	Grill, W.M. (1999) Modeling the Effects of Electric Fields on Nerve Fibers: Influence of Tissue Electrical Properties. IEEE Transactions on Bio-Medical Electronics, 46, 918-928. https://doi.org/10.1109/10.775401
[14]	Mueller, J.K. and Tyler, W.J. (2014) A Quantitative Overview of Biophysical Forces Impinging on Neural Function. Physical Biology, 11, Article ID: 051001. https://doi.org/10.1088/1478-3975/11/5/051001
[15]	Heimburg, T. (2014) Mechanical Aspects of Membrane Thermodynamics. Estimation of the Mechanical Properties of Lipid Membranes Close to the Chain Melting Transition from Calorimetry. Biochimica et Biophysica Acta—Biomembranes, 1415, 147-162. https://doi.org/10.1016/S0005-2736(98)00189-8
[16]	Tasaki, I., Kusano, K. and Byrne, M. (1989) Rapid Mechanical and Thermal Changes in the Garfish Olfactory Nerve Associated with a Propagated Impulse. Biophysical Journal, 55, 1033-1040. https://doi.org/10.1016/S0006-3495(89)82902-9
[17]	Tasaki, I. and Byrne, M. (1990) Volume Expansion of Nonmyelinated Nerve Fibers during Impulse Conduction. Biophysical Journal, 57, 633-635. https://doi.org/10.1016/S0006-3495(90)82580-7
[18]	Blunck, R. and Batulan, Z. (2012) Mechanism of Electromechanical Coupling in Voltage-Gated Potassium Channels. Frontiers in Pharmacology, 3, Article No. 166. https://doi.org/10.3389/fphar.2012.00166
[19]	Covarrubias, M., Barber, A.F., Carnevale, V., Treptow, W. and Eckenhof, R.G. (2015) Mechanistic Insights into the Modulation of Voltage-Gated Ion Channels by Inhalational Anesthetics. Biophysical Journal, 109, 2003-2011. https://doi.org/10.1016/j.bpj.2015.09.032
[20]	Heimburg, T. (2004) Mechanistic Insights into the Modulation of Voltage-Gated Ion Channels by Inhalational Anesthetics. Biochimica et Biophysica Acta—Biomembranes, 1662, 113.
[21]	Engelbrecht, J., Peets, T., Tamm, J., Laasmaa, M. and Vendelin, M. (2018) On the Complexity of Signal Propagation in Nerve Fibres. Proceedings of Estonian Academy of Science, 67, 28-38. https://doi.org/10.3176/proc.2017.4.28
[22]	Mengnjo A., Dikandé, A.M. and Ngwa, G. (2020) Model of the Nerve Impulse with Account of Mechanosensory Processes: Stationary Solutions. Journal of Applied Mathematics and Physics, 8, 2091-2102. https://doi.org/10.4236/jamp.2020.810156
[23]	Renardi, M. and Rogers, R. (2004) An Introduction to Partial Differential Equations. 2nd Edition, Springer, New York.