1. Introduction
In recent years, a new study set has begun to give unexpected connections among some problems relating to gravity aspects. It’s clear that quantum entanglement, quantum error correction, and computational complexity play a fundamental role in the spacetime geometry emergence. For instance, we have demonstrated in our first article [1] . These tools have substantial progress on black hole information problem, giving new avenues for searching for a tension resolution between black hole physics and quantum mechanics as TOUGMA’s theory; and all these solutions study is important to understand Universe properties.
TOUGMA’s theory, first published in 2021, is a geometric theory [2] ,
(1)
The solution imposed spherically symmetric metric, caused by no electrical charge and non-rotating n-dimensions massive object in vacuum. The method is used to calculating Ricci Tensor components for a metric general form for some conditions and by giving their equating to 0 [3] . This equation is solved by finding two solutions with one being real and it was studied [4] :
(2)
the other is complex:
(3)
Exploring the possibility of showing the effects of complex TOUGMA’s metric on systems is then necessary to know other universe properties that real solutions don’t show. In this work, we are going to find Radial Light Geodesics by assuming that light geodesic is a geodesic of zero length with
and
.
(4)
This metric is given by:
(5)
We are going to start with physics concepts at r = 0, which has been published in Study of Complex TOUGMA’s Metric [5] . Secondly, we are going to determine the light geodesics with the material bodies geodesics orbits.
2. Methods
A solution of TOUGMA’s equation that can be defined by the existence of a coordinate system
, called TOUGMA coordinates [6] [7] , such that the components
of the metric tensor g are written there:
(6)
Let us now examine the mass bodies trajectories(orbits) of
around of the central body of the TOUGMA metric [8] [9] [10] . These trajectories must be time-like geodesics. If the subsequent trajectory deviates towards one of the two hemispheres separated by this equator, this would represent a break in the spherical symmetry. Thus the particle must remain in the plane and for a specific
[11] [12] .
(7)
and
(8)
From Kelling vectors we have:
(9)
(10)
that implies:
(11)
(12)
the 5-components of the pentavector
are:
(13)
(14)
(15)
(16)
by
, it happens as we get:
(17)
(18)
(19)
(20)
(21)
the physicals phenomena of this are going to be studied in the next section.
3. Results
The potential equation is given by:
(22)
(23)
and the extremuns of
are given by [13] :
(24)
(25)
(26)
(27)
(28)
any solution r must verify:
(29)

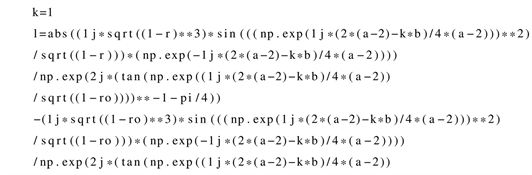

as shown Figure 1 and Figure 2 for a given quantum energy a parallel universe coexisted with the prime universe in the same space-time dimensional number n which explain cosmic expansion.
4. Scope of Future Work
The complex TOUGMA’s solution is crucial mostly the material bodies Orbits for understanding the matter behavior in quantum relativity universe properties. This solution areas used are exceptionally wide:
1) Astrophysics;
2) Cosmology;
3) Quantum gravity;
4) Quantum Mechanics;
5) Multiverse.
![]()
Figure 1. Incoming geodesics properties according to α.
![]()
Figure 2. Outgoing geodesics properties according to α.
The present investigation will be very helpful to the researchers who are engaged in those research work areas in unification of quantum mechanics and General Relativity. Our future work is to simulate these results and compare them with observations.
List of Symbols
: Dimensional number
: Ricci Tensor
: Quantum Lagrangian
: Metric Tensor
: Energy-Impulsion Tensor
: Curvature Tensor
: Energy per mass
: Impulsion per mass
: potential efficiency
: coordinate System