The Number of Primes

Pál Doroszlai, Horacio Keller

Independent Researcher, Kékkút, Hungary.

DOI: 10.4236/apm.2022.122008                

Abstract

It is known that the prime-number-formula at any distance from the origin has a systematic error. It is shown that this error is proportional to the square of the number of primes present up to the square root of the distance. The proposed completion of the prime-number-formula in the present paper eliminates this systematic error. This is achieved by using a quickly converging recursive formula. The remaining error is reduced to a symmetric dispersion of the effective number of primes around the completed prime-number-formula. The standard deviation of the symmetric dispersion at any distance is proportional to the number of primes present up to the square root of the distance. Therefore, the absolute value of the dispersion, relative to the number of primes is approaching zero and the number of primes resulting from the prime-number-formula represents the low limit of the number of primes at any distance.

Keywords

Prime-Number-Formula, Prime Gaps

1. Introduction

Writing the integral of de la Valée Poussin as summing over all integers the local density of primes results in a first approximation for the number of primes. The summing may be written as two steps: First summing up the local density of primes within sections of length ( $\sqrt{c}$ ) and then summing up to over all the ( $\sqrt{c}$ ) sections. As the first simplification over each section, the average of the local density is taken. A second simplification is taking instead the average of the local density of primes within each section, the density within the last section at the distance (c). This simplification results in the well-proved prime-number-formula. It is shown that the difference between the first simplification and the prime-number-formula is proportional to the square of the number of primes present up to the distance ( $\sqrt{c}$ ).

Further, it is shown that the error due to the first simplification is proportional to the number of primes present up to the distance ( $\sqrt{c}$ ). This proportionality allows for a correction of the first simplification. In fact, this correction may be applied recursively. Avoiding the second simplification, the resulting formula gives without systematic error the number of primes at the distance (c).

2. Evaluation of the Number of Primes

De la Valée Poussin proved 1899, (ref. [1] ), that ( $\pi \left(c\right)\approx Li\left(c\right)$ ), the integral of the local logarithmic density of free positions ( $1/\ln \left(c\right)$ ). Approximating the integral by the sum of the logarithmic density over all integers is in the following named as sum over all integers:

$\pi \left(c\right)+O\left(c\right)\approx {\displaystyle \underset{2}{\overset{c}{\int }}\frac{1}{\ln \left(c\right)}\text{d}c}$ ; ${\pi }_{appr}\left(c\right)\approx {\displaystyle \underset{n=2}{\overset{c}{\sum }}\frac{1}{\ln \left(c\right)}}$ (1.1)

The above sum may be written as summing up first over all integers within the sections of length ( $\sqrt{c}$ ) and then summing up to over all the ( $\sqrt{c}$ ) sections of the length ( $\sqrt{c}$ ). Taking the average value over each section and summing up to over the sections is the first simplification, in the following used as sum over all sections:

${\pi }_{appr}\approx {\displaystyle \underset{n=2}{\overset{c}{\sum }}\frac{1}{\ln \left(c\right)}}={\displaystyle \underset{j=2}{\overset{\sqrt{c}}{\sum }}\left[{\displaystyle \underset{n=\left(j-1\right)\sqrt{c}}{\overset{j\sqrt{c}}{\sum }}\frac{1}{\ln \left(c\right)}}\right]}\approx {\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}$ (1.2)

The well proven prime-number-formula PNF results from a second simplification of the above approximation by taking for each of the sections the smallest value of the density at ( $j=\sqrt{c}$ ):

${\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}>{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(\sqrt{c}\sqrt{c}\right)}}=\frac{c}{\ln \left(c\right)}=S\left(c\right)$ (1.3)

The difference between the first simplification of the number of primes and the value resulting from the PNF, (refs. [2] [3] ), is proportional to ( $R{\left(c\right)}^2=S{\left(\sqrt{c}\right)}^2$ ), the square of the number of primes up to the distance ( $\sqrt{c}$ ):

$\begin{array}{l}{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(\sqrt{c}\sqrt{c}\right)}}\\ ={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-\frac{\sqrt{c}}{\ln \left(c\right)}{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}1}={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-S\left(c\right)={\gamma }_{c}R{\left(c\right)}^2\end{array}$

because value ( ${\gamma }_c$ ) quickly converges to a constant value, as shown in Annex A1:

$\begin{array}{c}{\gamma }_c=\frac{\sqrt{c}}{\ln \left(c\right)R{\left(c\right)}^2}{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\left(\frac{\ln \left(c\right)}{\ln \left(j\sqrt{c}\right)}-\sqrt{c}\right)}\\ =\frac{1}{2R\left(c\right)}{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\left(\frac{\ln \left(c\right)}{\ln \left(j\sqrt{c}\right)}-\sqrt{c}\right)}\\ =\frac{1}{R\left(c\right)}{\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\left(\frac{\ln \left(\sqrt{c}\right)}{\ln \left(j\sqrt{c}\right)}-\frac{\sqrt{c}}{2}\right)}\end{array}$ (1.4)

Thus, the error of the second simplification resultinginthe PNF at the distance (c) is proportional to ( $R{\left(c\right)}^2$ ), the square of the number of primes present at ( $\sqrt{c}$ ). The factor of proportionality is evaluated in Annex A1 as ( ${\gamma }_c=0.2829\cdots$ ).

The relation between the error of the PNF at (c) and the square of the number of primes up to ( $\sqrt{c}$ ) is invariant. The constant factor of proportionality ( ${\gamma }_c$ ) is an inherent propriety of the number of primes.

The first simplification replacing ( ${\displaystyle \underset{n=\left(j-1\right)\sqrt{c}}{\overset{j\sqrt{c}}{\sum }}\frac{1}{\ln \left(n\right)}}$ ) by ( $\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}$ ) in (1.2) originates an error ( $\Delta {\pi }_{error}\left(c\right)$ ).

It can be proved, that this error is proportional to ( $R\left(c\right)$ ), the number of the series of multiples of primes, which are covering positions at (c). This is because each of the series of multiples of primes contributes its share to the error:

$\Delta {\pi }_{error}\left(c\right)={\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}\approx {\gamma }_{sec}\frac{\sqrt{\sqrt{c}}}{\ln \left(\sqrt{\sqrt{c}}\sqrt{\sqrt{c}}\right)}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}1}\approx {\gamma }_{sec}R\left(c\right)$ (1.5)

Herewith the error at the distance (c)—meaning the difference between the effective number of primes ( $\pi \left(c\right)$ ) and the value resulting from the first simplification ( ${\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)$ ), using the average value of the density over the sections in (1.2)—is proportional to the number of primes up to ( $\sqrt{c}$ ). The factor of proportionality is evaluated in annex 2.2:

$\Delta {\pi }_{error}\left(c\right)={\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)-\pi \left(c\right)={\gamma }_{sec}R\left(c\right)$ ; ${\gamma }_{sec}=-0.03551$ (1.6)

Because the error of the first simplification resulting from the procedure of taking the average of the number of primes over the sections—evaluated as sum over all sections (1.2)—is proportional to the number of primes present up to the root of the distance, the approximating function (1.2) may be corrected correspondingly. The corrected approximating function, the corrected sum over all sections is instead of (1.2):

$\begin{array}{c}{\pi }_{sec\text{\_}appr\text{\_}corr\text{\_}}\left(c\right)={\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)-{\gamma }_{sec}{\pi }_{sec\text{\_}appr\text{\_}}\left(\sqrt{c}\right)\\ ={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-{\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}\end{array}$ (1.7)

But herewith for ( $R_{eff}\left(c\right)$ ) and for ( $S_{eff}\left(c\right)$ ) it may be written recursively:

$\begin{array}{c}{\pi }_{sqr\text{\_}sec\text{\_}appr\text{\_}corr\text{\_}}\left(c\right)={\pi }_{sqr\text{\_}sec\text{\_}appr\text{\_}}\left(c\right)-{\gamma }_{sec}{\pi }_{sqr\text{\_}sec\text{\_}appr\text{\_}}\left(\sqrt{c}\right)\\ ={\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}-{\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{\sqrt{c}}}}{\sum }}\frac{\sqrt{\sqrt{\sqrt{c}}}}{\ln (\; j\; c\; )}}\end{array}$

$\begin{array}{c}{\pi }_{sec\text{\_}appr\text{\_}corr\text{\_}}\left(c\right)={\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)-{\gamma }_{sec}{\pi }_{sec\text{\_}appr\text{\_}}\left(\sqrt{c}\right)\\ ={\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)-{\gamma }_{sec}\left({\pi }_{sqr\text{\_}sec\text{\_}appr\text{\_}}\left(c\right)-{\gamma }_{sec}{\pi }_{sqr\text{\_}sqr\text{\_}sec\text{\_}appr\text{\_}}\left(\sqrt{c}\right)\right)\\ ={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-{\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}+{\gamma }_{sec}^2{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{\sqrt{c}}}}{\sum }}\frac{\sqrt{\sqrt{\sqrt{c}}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}+\cdots \end{array}$ (1.8)

This allows writing for the complete-prime-number-formula (CPNF):

${\pi }_{appr\text{\_}}\left(c\right)={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-{\displaystyle \underset{m=1}{\overset{\infty }{\sum }}{\gamma }_{sec}^m}{\displaystyle \underset{j=1}{\overset{c^{\left(\frac{1}{2^{m+1}}\right)}}{\sum }}\frac{c^{\left(\frac{1}{2^{m+1}}\right)}}{\ln \left(j\cdot c^{\left(\frac{1}{2^{m+1}}\right)}\right)}}$ (1.9)

This formula convergevery fast: Two steps with ( $m=2$ ) are already sufficient.

The results of the CPNF are evaluated in Annex A3and compared with the effective number of primes. Compared with another approximating formula (refs. [4] [5] ), there is no systematic error. The remaining error is the dispersion around the CPNF. It is proportional to the number of primes up to ( $R\left(c\right)$ ), the series of multiples that are covering positions at (c). Therefore, the dispersion of the effective number of primes around the CPNF, relative to ( $R\left(c\right)$ ) has constant boundaries, symmetrical around zero, as demonstrated in AnnexA2 and AnnexA3:

$\Delta {\pi }_{appr\text{\_}rel\text{\_}}\left(c\right)=\frac{{\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)-\pi \left(c\right)}{R\left(c\right)}$ ; $\Delta {\pi }_{sqr\text{\_}appr\text{\_}rel\text{\_}}\left(c\right)=\frac{{\pi }_{sqr\text{\_}sec\text{\_}appr\text{\_}}\left(c\right)-\pi \left(\sqrt{c}\right)}{R\left(\sqrt{c}\right)}$ (1.10)

The standard deviation of the relative dispersion is:

$S{D}_{\Delta \pi \text{\_}appr\text{\_}rel\text{\_}}\left(c\right)=\sqrt{\frac{1}{c}{\displaystyle \underset{c}{\sum }{\left(\frac{{\pi }_{appr}\left(c\right)-{\pi }_{eff}\left(c\right)}{{\pi }_{eff}\left(\sqrt{c}\right)}\right)}^2}}$ (1.11)

It is evaluated in Annex A4. It is found that the standard deviation is constant over the distance. This constant is evaluated in Annex A4as ( $F_{SD\text{\_}\Delta \pi }=0.16238$ ), it is again an inherent property of the prime numbers.

3. Boundaries of the Dispersion of the Number of Primes around the CPNF

Regarding FigureA3.1, it is obvious, that the dispersion shows oscillations of different frequencies: There are different oscillations with high, middle, and low frequencies observable. The evaluation of the number of primes with the CPNF correct the error of the average on the long range, but at the same time it is the origin of oscillations due to the summation procedures over ( $R\left(c\right)$, $R\left(\sqrt{c}\right)$, $R\left(\sqrt{\sqrt{c}}\right)$, $\cdots$ ) subsections. Each time these values change by unity, there is a discontinuity in the summation procedure. At the distance (c), with ( $R\left(c\right)$ ) being the number of primes present up to ( $\sqrt{c}$ ), the summing of the local density values over (j) is influenced only by ( $\sqrt{c}$ ). If for the distance succeeding primes were taken, as in the above evaluations, the size of the gaps between primes would account for the long-range fluctuations. If ( $R\left(c\right)$ ) changes by unity, there is a jump: At the change of the distance at certain number of primes ( $P_{\left(n\right)}$ ) the summation limit changes

from ( $n=R\left(c\right)$, $c=P_{\left(n\right)}$ ) to ( $n=R\left(c\right)+1$, $c=P_{\left(n+1\right)}$ ),

from ( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}$ ) to ( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)+1}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}$ ) (2.1)

The difference makes

( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)+1}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}-\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}\approx \frac{\sqrt{c}}{\ln \left(c\right)}=\frac{R\left(c\right)}{2}$ ). (2.2)

For illustration, the discontinuity of the approximating function is evaluated and illustrated in Annex A5.

Thus, the dispersion of the effective number of the primes around the best estimate value—due to the evaluation procedure of the best estimate value—is proportional to the number of primes, the series of multiples of which primes cover positions at the distance (c). Another source of dispersion is the variable gap between the primes. Concerning the complete dispersion, the following lemma may be formulated:

Lemma 2.1:

The boundaries of the dispersion of the number of primes at any distance (c) are proportional to ( $R\left(c\right)$ ), the number of the series of multiples of primes, which are covering positions at (c).

Proof: The cover interval is defined as the interval of the size ( $2\sqrt{c}$ ) with centrum at the distance (c). Shifting the centrum of the cover interval to the origin, all the series of multiples of the ( $R\left(c\right)$ ) primes coincide, and each series covers at least two positions within the cover interval, around the origin. Such a complete coincidence occurs next times at the distance equal to the product of all first ( $R\left(c\right)$ ) primes.

In the following, only the series of multiples of the primes in the range ( $P_{\left(n\right)}$, $R\left(\sqrt{c}\right)<n<R\left(c\right)$ ) will be taken into consideration. This does not influence the validity of the proof, since for large distances nearly all primes are in this range.

At any distance ( $\sqrt{c}\cdots c$ ) all of the series of multiples of primes are shifted with reference to (c), except the ones coinciding at (c). All these shifted series liberate by the shifting two positions within the cover interval. The series of multiples of some primes—after the shifting—may cover again two positions, which are liberated by the shifting of the series of multiples of two other primes. This is only possible, if the corresponding prime is—before the shifting—equidistant to two other primes. It can be proved, that the density of the number of such three equidistant primes at the distance (c) is ( $\frac{{\delta }_{2}c}{\ln {\left(c\right)}^3}$ ; ${\delta }_2=1.320323632$ ), thus ( $\frac{{\delta }_2}{\ln {\left(c\right)}^2}$ ) times smaller, then the density of primes.

Because of this fact, the effect of the multiple coverage after the shiftingmay be neglected: On the average, each shifted series of multiples of primes liberates two positions within the cover interval and covers only one.

Herewith the shifted series of multiples of the ( $R\left(c\right)-R\left(\sqrt{c}\right)$ ) primes leave on the average ( $R\left(c\right)-R\left(\sqrt{c}\right)$ ) positions free within the cover interval. These free positions are for a large distance about equally distributed between the upper and the lower part of the cover interval. Therefore, within the sections of the length ( $\sqrt{c}$ ) at the arbitrary distance (c) there are, on the average

( $\frac{1}{2}\left(R\left(c\right)-R\left(\sqrt{c}\right)\right)\approx \frac{1}{2}R\left(c\right)$ ) positions left free.

Besides the effect of the multiple coverages, there are some other effects, which may be the reason for divergence from the average value ( $R\left(c\right)/2$ ). All the following effects may be neglected:

The effect of multiple coincidences between the series of multiples of primes: The number of coinciding primes ( $q=Q\left(c\right)$ ) is limited by the fact, that their product must be smaller than the distance (c). The largest number of coincidences occurs, if the first (q) primes are coinciding:

$Per\left(q\right)={\displaystyle \underset{p=1}{\overset{q}{\prod }}{P}_{\left(p\right)}}$ ; $Q\left(c\right)=Per\left(q\right)$ ; $Per\left(q\right)\le c<Per\left(q+1\right)$ (2.3)

The number ( $Q\left(c\right)$ ) is growing very slowly with the distance (c). Its effect may be neglected against ( $R\left(c\right)/2$ ), the average value of free positions remaining.

The effect of the shifting outside of the cover interval: Each series of multiples considered may cover two positions within the cover interval after the shifting. By the shifting, the covering capability of some series of multiples of primes may be reduced by shifting outside of the limits of the cover interval one of the covered positions. The number of covered positions within the cover interval may only be reduced by this effect, herewith rising the remaining number of the remaining free positions. The number of the primes, which may participate in this effect is limited, therefore the effect may be neglected against ( $\frac{1}{2}R\left(c\right)$ ), the average value of free positions remaining.

Therefore, the total dispersion is proportional to ( $\frac{1}{2}R\left(c\right)$ ), as stated in the lemma and concluding the proof.

With this lemma the dispersion of the number of primes within each section of the length ( $\sqrt{c}$ ) at the distance ( $j\sqrt{c}$ ) is certainly smaller than the average number of free positions left ( $\frac{1}{2}R\left(c\right)$ ). Therefore, the difference between the effective value of primes up to this distance ( $\pi \left(c\right)$ ) and its approximation ( ${\pi }_{appr}\left(c\right)$ ) is limited to the number of the series of multiples of primes, which are covering positions at this distance:

${\pi }_{bounds\text{\_}eff}\left(c\right)=\pm \frac{\sqrt{c}}{2\ln \left(c\right)}$ ;

${\pi }_{bounds}\left(c\right){\pi }_{bounds}\left(c\right)={\pi }_{bounds\text{\_}appr}\left(c\right)+{\pi }_{bounds\text{\_}eff}\left(c\right)=\pm \frac{\sqrt{c}}{\ln \left(c\right)}=\pm R\left(c\right)$ (2.4)

Lemma 2.1 is in accordance with the fact—demonstrated in (1.11) and in Annex A4—that the standard deviation of the dispersion around the best estimate approximation of the number of primes—resulting from the CPNF, and relative to ( $R\left(c\right)$ )—is constant over the distance (c). The constancy of the standard deviation of the relative dispersion around the best estimate approximation of the number of primes—resulting from the CPNF—is an inherent property of the prime numbers.

From Lemma 2.1, the boundary of the dispersion of the effective number of primes around the value resulting from its best estimate expression is proportional to the number of primes, which are covering position at any distance from the origin ( $K\cdot R\left(c\right)$ ), with (K) being a constant factor of any size):

$\underset{c\to \infty }{\lim }{\pi }_{disp}\left(c\right)=\underset{c\to \infty }{\lim }\left(K\cdot {\pi }_{bounds\text{\_}eff}\left(c\right)\right)=\underset{c\to \infty }{\lim }\left(K\cdot R\left(c\right)\right)=\infty$ (2.5)

With this boundary growing to infinity, an additional proof for the fact, which the upper limit of the gap between consecutive primes is unlimited, (see ref. [6] ). On the other hand, it follows, that the width of the boundaries of the dispersion of the number of primes, relative to the value resulting from its best estimate expression, is approaching zero with the distance growing without limit:

$\frac{{\pi }_{disp}\left(c\right)}{\pi \left(c\right)}=\frac{K\cdot {\pi }_{bounds\text{\_}eff}\left(c\right)}{\pi \left(c\right)}=\frac{K\cdot R\left(c\right)}{S\left(c\right)}:\underset{c\to \infty }{\lim }\left(\frac{\frac{K\cdot \sqrt{c}}{\ln \left(\sqrt{c}\right)}}{\frac{c}{\ln \left(c\right)}}\right)=\underset{c\to \infty }{\lim }\frac{2\cdot K}{\sqrt{c}}=0$ (2.6)

Therefore, the series of primes approaches a continuum for large distances.

Lemma 2.2:

For any distance from the origin (c) large enough, the difference between the values resulting from the complete-prime-number-formula (CPNF) and from the prime-number-formula (PNF) is larger than the width of the dispersion of the number of primes ( $R\left(c\right)$ ) multiplied by any constant factor ( $K\ge 1$ ).

Proof: The difference between the value of the (CPNF) and the (PNF) is with (1.3) growing proportional to ( $R{\left(c\right)}^2$ ), with the factor of proportionality ( ${\gamma }_c$ ). The width of the dispersion of the number of primes grows with Lemma 2.1 only proportional to ( $R\left(c\right)$ ).

For any sufficiently large distance ( $c_{limit}\left({\gamma }_c\right)<c$ ) the difference between the value of the (CPNF) and the (PNF) outgrows ( $K\cdot R\left(c\right)$ ) for any (K):

$\underset{c\to \infty }{\lim }\frac{\pi \left(c\right)-S\left(c\right)}{K\cdot R\left(c\right)}=\frac{{\gamma }_c}{K}R\left(c\right)=\infty$

asstated in the lemma and concluding the proof.

From this Lemma 2.2 follows, that the PNF is the low limit of the number of primes. Because the number of primes has a low limit function, growing to infinity, it is infinite itself: An additional proof for the infinity of the number of primes.

4. Conclusions

For large distances, the CPNF gives a result for the number of primes as good as de la Valée Poussin’s formula: There is no systematic error involved. The explication for this fact is that de la Valée Poussin’s formula uses the integral of the local density given by the inverse of the logarithm, while Equation (1.0) uses the summation of the same values, applied over the sections of the length ( $\sqrt{c}$ ), with recurring correction. This allows to formulate the following lemma:

Lemma 3.1:

The complete-prime-number-formula (CPNF) gives the number of primes with increasing efficiency for all distances from the origin.

Proof: The approximating formula (1.9) is based on the recurring application of the correction of the replacement of the de la Valée Poussin integral:

${\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}-{\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}+{\gamma }_{sec}^2{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{\sqrt{c}}}}{\sum }}\frac{\sqrt{\sqrt{\sqrt{c}}}}{\ln \left(j\sqrt{\sqrt{\sqrt{c}}}\right)}}+\cdots$

For large distances (c) each of the components of the correction goes over into the integral of the inverse of the logarithm of the distance (c):

$\underset{c\to \infty }{\lim }\left({\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}\right)={\displaystyle \underset{0}{\overset{c}{\int }}\frac{1}{\ln \left(c\right)}\text{d}c}$ ; ${\gamma }_{sec}{\displaystyle \underset{j=1}{\overset{\sqrt{\sqrt{c}}}{\sum }}\frac{\sqrt{\sqrt{c}}}{\ln \left(j\sqrt{\sqrt{c}}\right)}}={\gamma }_{sec}{\displaystyle \underset{0}{\overset{\sqrt{c}}{\int }}\frac{1}{\ln \left(\sqrt{c}\right)}\text{d}c}$

For the distance (c) growing to infinity, the contribution of the successive components—relative to the effective number of primes approaches zero. The remaining first component results in the de la Valée Poussin integral as stated in the lemma and concluding the proof.

The first evaluation of the factor ( ${\gamma }_c$ ) in (1.6) and (1.7) is somewhat heuristic since the convergence is not strongly proved. But the application of this factor in the CPNF results in a converging approximation of the effective number of primes. This fact justifies the evaluation procedure of the factor ( ${\gamma }_{sec}$ ) and proves the validity of its value. The evaluation of the factor ( ${\gamma }_{sec}$ ) is repeated in Annex A3 with the results of the CPNF. It gives the exact value.

Annexes

All above formula are checked in the following annexes with numeric results. The annexes together compose executable files in MATHCAD from PTC. The syntax corresponds to the MATHCAD syntax. Especially the symbols ( $ceil\left(x\right)$ ) and ( $floor\left(x\right)$ ) stand for rounding up or down a real value to the next larger respectively to the next smaller integer.

Annex 0: General Data, Vectors, and Functions

In the following all formula are checked with numeric results. The set of primes and the listed known formula below are used for this checking. Some vectors of the results of the known formula, which are often used, are evaluated and the results are saved.

The set of primes is read from a file: ( $P:=\text{READPRN}\left("\text{PRimes\_large}\text{.prn}"\right)$ ). The number of primes in the set and their numbering are: ( $N_P:=\text{rows}\left(P\right)-1=5003713$, $n:=1,2,\cdots ,N_P$ ).

The number of primes up to (c) is approximated with the prime-number-formula ( $S\left(c\right)$ ). At (c) only the multiples of the primes up to ( $\sqrt{c}$ ) are covering free integral positions ( $R\left(c\right)=S\left(\sqrt{c}\right)$ ). The numbers of these primes are given as well:

$P_{\left(S\left(c\right)\right)}<c<P_{\left(S\left(c\right)+1\right)}$ ; ${\pi }_c\left(c\right)>S\left(c\right):=\text{floor}\left(\frac{c}{\ln \left(c\right)}\right)\approx \frac{c}{\ln \left(c\right)}$ (A0.1)

$P_{\left(R\left(c\right)\right)}<\sqrt{c}<P_{\left(R\left(c\right)+1\right)}$ ; ${\pi }_c\left(\sqrt{c}\right)>S\left(\sqrt{c}\right)=R\left(c\right):=\text{floor}\left(\frac{\sqrt{c}}{\ln \left(\sqrt{c}\right)}\right)\approx \frac{\sqrt{c}}{\ln (\; c\; )}$

For the evaluation of the effective number of free positions up to the distance (c) the routine ( $n_{next}\left(c,n_{last}\right)$ ) resulting the index (n) of the prime next to any integer is needed ( $P_{\left(n\right)}\le c<P_{\left(n+1\right)}$ ). The evaluation starts either at the last evaluated index ( $n_{last}$ ), or at the index resulting from the prime-number-formula. This, to shorten some of the evaluation processes. Further functions are the indexes of the closest primes to any distance, and to the square root of any distance, as well as a short expression for the exponential function:

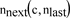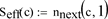
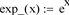=;; (A0.2)

In the following all functions, which are evaluated for illustration, are evaluated at sparse distances, equal to multiples of the square root of the largest

distance considered ( $c_{s{p}_{\left(k\right)}}=k\sqrt{P_{\left(N_P\right)}}$ ):

$\Delta c_{sp}:=\sqrt{P_{\left(N_P\right)}}$ ; $k_{limit}:=\text{floor}\left[\frac{P_{\left(N_P\right)}}{\Delta c_{sp}}\right]-1=9277$ ;

$k:=1,2,\cdots ,k_{limit}$ ; $c_{s{p}_{\left(k\right)}}:=k\cdot \Delta c_{sp}$ (A0.3)

The vectors of the indexes of the primes corresponding to these sparse distances, respectively to the next smaller primes ( $P_{\left[n_{s{p}_{\left(k\right)}}\right]}<c_{s{p}_{\left(k\right)}}<P_{\left[n_{s{p}_{\left(k+1\right)}}\right]}$ ) are evaluated for ( ${\pi }_{sp}\left(c\right)$ ), ( ${\pi }_{sp}\left(\sqrt{c}\right)$ ), and ( ${\pi }_{sp}\left(\sqrt{\sqrt{c}}\right)$ ). They are evaluated once and written to files. They are read from these files:

${\pi }_{s{p}_{\left(k\right)}}:=n_{next}\left[c_{s{p}_{\left(k\right)}},1\right]$ ; ${\pi }_{sqr\text{\_}s{p}_{\left(k\right)}}:=n_{next}\left[\sqrt{c_{s{p}_{\left(k\right)}}},1\right]$ ;

${\pi }_{sqr\text{\_}sqr\text{\_}s{p}_{\left(k\right)}}:=n_{next}\left[\sqrt{\sqrt{c_{s{p}_{\left(k\right)}}}},1\right]$ (A0.4)

$\text{WRITEPRN}\left("\text{index\_distance\_sp}\text{.prn}"\right):={\pi }_{sp}$ ; ${\pi }_{sp}:=\text{READPRN}\left("\text{index\_distance\_sp}\text{.prn}"\right)$ ; $\text{length}\left({\pi }_{sp}\right)=9278$

$\text{WRITEPRN}\left("\text{n\_sqr\_sp\_primes}\text{.prn}"\right):={\pi }_{sqr\text{\_}sp}$ ; ${\pi }_{sqr\text{\_}sp}:=\text{READPRN}\left("\text{n\_sqr\_sp\_primes}\text{.prn}"\right)$ ; $\text{length}\left({\pi }_{sqr\text{\_}sp}\right)=9278$

$\text{WRITEPRN}\left("\text{n\_sqr\_sqr\_sp\_primes}\text{.prn}"\right):={\pi }_{sqr\text{\_}sqr\text{\_}sp}$ ; ${\pi }_{sqr\text{\_}sqr\text{\_}sp}:=\text{READPRN}\left("\text{n\_sqr\_sqr\_sp\_primes}\text{.prn}"\right)$

Annex 1. Evaluation of the Number of Primes as Sum over Sections

The number of primes as sum over sections is evaluated with (1.2) as a first simplification:

${\pi }_{sec\text{\_}appr\text{\_}}\left(c\right)={\displaystyle \underset{j=1}{\overset{\sqrt{c}}{\sum }}\frac{\sqrt{c}}{\ln \left(j\sqrt{c}\right)}}$ (A1.1)

The number of primes resulting from the second simplification (1.3) results the PNF. The difference between the first and the second simplification results the error of the PNF. At the dinstance (c) it is proportional to ( $R{\left(c\right)}^2$ ), the square of the number of primes covering positions at the distance ( $\sqrt{c}$ ). The factor of proportionality is evaluated over the distance with (1.4):

${\gamma }_{c\text{\_}appr{\text{\_}}_{\left(k\right)}}:=\frac{1}{R\left[c_{s{p}_{\left(k\right)}}\right]}\left[{\displaystyle \underset{j=1}{\overset{ceil\left[\sqrt{c_{s{p}_{\left(k\right)}}}\right]}{\sum }}\frac{\ln \left[\sqrt{c_{s{p}_{\left(k\right)}}}\right]}{\ln \left[j\sqrt{c_{s{p}_{\left(k\right)}}}\right]}-\frac{1}{2}\sqrt{c_{s{p}_{\left(k\right)}}}}\right]$ (A1.2)

The factors are evaluated once and written to a file. They are read from this file:

$\text{WRITEPRN}\left("\text{gamma\_c\_appr\_sp}\text{.prn}"\right):={\gamma }_{c\text{\_}appr\text{\_}}$ ; ${\gamma }_{c\text{\_}appr\text{\_}}:=\text{READPRN}\left("\text{gamma\_c\_appr\_sp}\text{.prn}"\right)$

The factors are approaching a constant value: (FigureA1.1)

${\gamma }_{c\text{\_}appr}:={\gamma }_{c\text{\_}appr{\text{\_}}_{\left(k_{limit}\right)}}=0.28312$

Figure A1.1. Relation of the error of the prime-number-formula to the square of the number of the series of multiples of primes, which are covering positions, over the distance.

The approximating function is evaluated at sparse distances, respectively at the next smaller prime to these distances ( $P_{\left[n_{s{p}_{\left(k\right)}}\right]}<c_{s{p}_{\left(k\right)}}<P_{\left[n_{s{p}_{\left(k+1\right)}}\right]}$ ) with (1.2). They are evaluated similarly as well at the square root and at the square root of the square root of these sparse distances. The evaluation at the next smaller prime corresponding to each distance assures that the evaluated numbers of the primes correspond exactly to the distances considered:

${\pi }_{sec\text{\_}app{r}_{\left(k\right)}}:={\pi }_{sec\text{\_}appr\text{\_}}\left[P_{\left[{\pi }_{s{p}_{\left(k\right)}}\right]}\right]$ ; ${\pi }_{sqr\text{\_}sec\text{\_}app{r}_{\left(k\right)}}:={\pi }_{sec\text{\_}appr\text{\_}}\left[P_{\left[{\pi }_{sqr\text{\_}s{p}_{\left(k\right)}}\right]}\right]$ (A1.3)

${\pi }_{sqr\text{\_}sqr\text{\_}sec\text{\_}app{r}_{\left(k\right)}}:={\pi }_{sec\text{\_}appr\text{\_}}\left[P_{\left[{\pi }_{sqr\text{\_}sqr\text{\_}s{p}_{\left(k\right)}}\right]}\right]$

They are evaluated once and written to files. They are read from these files:

$\text{WRITEPRN}\left("\text{pr\_sec\_appr\_sp\_t}\text{.prn}"\right):={\pi }_{sec\text{\_}appr}$ ; ${\pi }_{sec\text{\_}appr}:=\text{READPRN}\left("\text{pr\_sec\_appr\_sp\_t}\text{.prn}"\right)$ ;

$\text{WRITEPRN}\left("\text{pr\_sqr\_sec\_appr\_sp\_t}\text{.prn}"\right):={\pi }_{sqr\text{\_}sec\text{\_}appr}$ ; ${\pi }_{sqr\text{\_}sec\text{\_}appr}:=\text{READPRN}\left("\text{pr\_sqr\_sec\_appr\_sp\_t}\text{.prn}"\right)$ ;

$\text{WRITEPRN}\left("\text{pr\_sqr\_sqr\_sec\_appr\_sp\_t}\text{.prn}"\right):={\pi }_{sqr\text{\_}sqr\text{\_}sec\text{\_}appr}$ ; ${\pi }_{sqr\text{\_}sqr\text{\_}sec\text{\_}appr}:=\text{READPRN}\left("\text{pr\_sqr\_sqr\_sec\_appr\_sp\_t}\text{.prn}"\right)$

Annex A2. Evaluation of the Factor of Correction of the First Simplification

The result of the first simplification (1.2) giving the sum over the sections of the density of primes has an error. This error is proportional to the number of primes up to ( $\sqrt{c}$ ). The error relative to ( $\pi \left(\sqrt{c}\right)$ ) results the factor of correction. Assuming the factor of correction ( ${\gamma }_{sec}$ ) is constant over the distance (c), it may be evaluated as relation of the average error to the effective number of primes ( $\pi \left(\sqrt{c}\right)={\pi }_{s{p}_{\left(k\right)}}$ ). The average error is:

$\Delta {\pi }_{se{c}_{\left(k\right)}}:={\pi }_{sec\text{\_}app{r}_{\left(k\right)}}-{\pi }_{s{p}_{\left(k\right)}}$ ; $\Delta {\pi }_{sec\text{\_}a{v}_{\left(k\right)}}:=\frac{1}{k}{\displaystyle \underset{j=1}{\overset{k}{\sum }}\left[\Delta {\pi }_{se{c}_{\left(j\right)}}\right]}$ (A2.1)

The value of the factor of correction is herewith:

Figure A2.1. Convergence of the relation of the average relative error of the first simplification (1.2) to the final constant value ( ${\gamma }_{sec}$ ).

${\gamma }_{sec}\left(c\right)=\frac{\Delta {\pi }_{sec\text{\_}av}\left(c\right)}{\pi \left(\sqrt{c}\right)}$ ; ${\gamma }_{sec{\_}_{\left(k\right)}}:=\frac{\sqrt{2}\Delta {\pi }_{sec\text{\_}a{v}_{\left(k\right)}}}{{\pi }_{sqr\text{\_}sec\text{\_}app{r}_{\left(k\right)}}}$ ; ${\gamma }_{sec}:={\gamma }_{sec{\_}_{\left(k_{limit}\right)}}=-0.035513$ (A2.2)

FigureA2.1 shows the independence of the factor of correction ( ${\gamma }_{sec}$ ) from the distance. The averaging process (A2.1) to evaluate the factor of correction is therefore justified. This factor ( ${\gamma }_{sec}=-0.035513$ ) is invariant, an inherent property of the prime numbers:

Annex A3. Evaluation of the CPNF

The CPNF (1.9) is evaluated with the following routine:

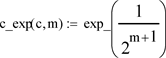; (A3.1)

The results of the CPNF are evaluated once at sparse values of the distance ( $c_{s{p}_{\left(k\right)}}$ ), for (c), ( $\sqrt{c}$ ) and ( $\sqrt{\sqrt{c}}$ ). They are written to files and are read from these files:

$\text{WRITEPRN}\left("\text{Pi\_appr\_sp}\text{.prn}"\right):={\pi }_{appr}$, ${\pi }_{appr}:=\text{READPRN}\left("\text{Pi\_appr\_sp}\text{.prn}"\right)$,

$\text{WRITEPRN}\left("\text{Pi\_sqr\_appr\_sp}\text{.prn}"\right):={\pi }_{sqr\text{\_}appr}$, ${\pi }_{sqr\text{\_}appr}:=\text{READPRN}\left("\text{Pi\_sqr\_appr\_sp}\text{.prn}"\right)$

$\text{WRITEPRN}\left("\text{Pi\_sqr\_sqr\_appr\_sp}\text{.prn}"\right):={\pi }_{sqr\text{\_}sqr\text{\_}appr}$, ${\pi }_{sqr\text{\_}sqr\text{\_}appr}:=\text{READPRN}\left("\text{Pi\_sqr\_sqr\_appr\_sp}\text{.prn}"\right)$.

Figure A3.1. The relative dispersion of the difference between the effective number of primes and its value evaluated with the complete-prime-number-formula (CPNF).

Figure A3.2. Relation of the error of the PNF to ( $R{\left(c\right)}^2$ ), the square of the number of primes up to ( $\sqrt{c}$ ), over the distance.

${\pi }_{app{r}_{\left(k\right)}}:={\pi }_{appr\text{\_}}\left[P_{\left[{\pi }_{s{p}_{\left(k\right)}}\right]}\right]$ ; ${\pi }_{sqr\text{\_}app{r}_{\left(k\right)}}:={\pi }_{appr\text{\_}}\left[P_{\left[{\pi }_{sqr\text{\_}s{p}_{\left(k\right)}}\right]}\right]$ ;

${\pi }_{sqr\text{\_}sqr\text{\_}app{r}_{\left(k\right)}}:={\pi }_{appr\text{\_}}\left[P_{\left[{\pi }_{sqr\text{\_}sqr\text{\_}s{p}_{\left(k\right)}}\right]}\right]$ (A3.2)

(FigureA3.1) There is no systematic error of the number of primes resulting with the CPNF. The dispersion of the evaluated values relative to the effective number of primes at ( $\sqrt{c}$ ) is about constant over the distance up to (c), ( $\sqrt{c}$ ) and ( $\sqrt{\sqrt{c}}$ ):

$\Delta {\pi }_{appr\text{\_}re{l}_{\left(k\right)}}:=\frac{{\pi }_{app{r}_{\left(k\right)}}-{\pi }_{s{p}_{\left(k\right)}}}{R\left[1\cdot c_{s{p}_{\left(k\right)}}\right]}$ ; $\Delta {\pi }_{sqr\text{\_}appr\text{\_}re{l}_{\left(k\right)}}:=\frac{{\pi }_{sqr\text{\_}app{r}_{\left(k\right)}}-{\pi }_{sqr\text{\_}s{p}_{\left(k\right)}}}{R\left[\sqrt{1\cdot c_{s{p}_{\left(k\right)}}}\right]}$ (A3.3)

$\Delta {\pi }_{sqr\text{\_}sqr\text{\_}appr\text{\_}re{l}_{\left(k\right)}}:=\frac{{\pi }_{sqr\text{\_}sqr\text{\_}app{r}_{\left(k\right)}}-{\pi }_{sqr\text{\_}sqr\text{\_}s{p}_{\left(k\right)}}}{R\left[\sqrt{\sqrt{1\cdot c_{s{p}_{\left(k\right)}}}}\right]}$

with the results of the CPNF the factor of the proportionality ( ${\gamma }_c$ ) of the error of the PNF relative to the square of the number of primes present up to ( $\sqrt{c}$ ) evaluated in (A1.2) with (1.4), is reevaluated with the more exact difference as follows: (FigureA3.2)

$\frac{{\pi }_{appr\text{\_}cpnf\text{\_}}\left(c\right)}{R{\left(c\right)}^2}={\gamma }_{cpnf{\text{\_}}_{\left(k\right)}}:=\frac{{\pi }_{app{r}_{\left(k\right)}}-s\left[c_{s{p}_{\left(k\right)}}\right]}{R{\left[c_{s{p}_{\left(k\right)}}\right]}^2}$ (A3.4)

Annex A4. Evaluation of the Standard Deviation of the Dispersion of the Effective Number of Primes around the CPNF

The standard deviation SD of the relative dispersion (1.13) is evaluated as follows:

$S{D}_{\Delta \pi \text{\_}appr\text{\_}re{l}_{\left(k\right)}}:=\sqrt{\frac{1}{k}{\displaystyle \underset{j=1}{\overset{k}{\sum }}\frac{{\left[{\pi }_{app{r}_{\left(j\right)}}-{\pi }_{s{p}_{\left(j\right)}}\right]}^2}{R_{eff}{\left[c_{s{p}_{\left(j\right)}}\right]}^2}}}$ (A4.1)

The results are evaluated once and written to a file: ( $\text{WRITEPRN}\left("\text{SD\_}\Delta \text{prime\_sqr\_appr\_rel}\text{.prn}"\right):=S{D}_{\Delta \pi \text{\_}appr\text{\_}rel}$ ). They are read from this file: ( $S{D}_{\Delta \pi \text{\_}appr\text{\_}rel}:=\text{READPRN}\left("\text{SD\_}\Delta \text{prime\_sqr\_appr\_rel}\text{.prn}"\right)$ ).

The average of the relation of the standard deviation converges to a final value, to the factor of proportionality ( $F_{SD\_\Delta \pi }$ ). This factor is evaluated as follows:

$S{D}_{\Delta \pi \text{\_}appr\text{\_}rel\text{\_}a{v}_{\left(k\right)}}:=\frac{1}{k}{\displaystyle \underset{j=1}{\overset{k}{\sum }}S{D}_{\Delta \pi \text{\_}appr\text{\_}re{l}_{\left(j\right)}}}$ (A4.2)

The results are evaluated once and written to a file. They are read from this file:

$\text{WRITEPRN}\left("\text{SD\_}\Delta \text{prime\_sqr\_appr\_rel\_av}\text{.prn}"\right):=S{D}_{\Delta \pi \text{\_}appr\text{\_}rel\text{\_}av}$ $S{D}_{\Delta \pi \text{\_}appr\text{\_}rel\text{\_}av}:=\text{READPRN}\left("\text{SD\_}\Delta \text{prime\_sqr\_appr\_rel\_av}\text{.prn}"\right)$

The constant factor is equal to the final average value of the standard deviation at large distances. The figure below illustrates that the standard deviation is about constant over the distance. This fact rectifies taking the average over the whole distance for the evaluation:

$F_{SD\text{\_}\Delta \pi }:=S{D}_{\Delta \pi \text{\_}appr\text{\_}rel\text{\_}a{v}_{\left(k_{limit}-1\right)}}=0.162389$ ;

$S{D}_{\pi }\left(c\right)$ $S{D}_{\Delta \pi \text{\_}sp\text{\_}rel\text{\_}a{v}_{\left(k\right)}}\cdot R\left(c\right)\approx F_{SD\text{\_}\Delta \pi }$ (A4.3)

FigureA4.1 below indicates that the standard deviation of the dispersion of the effective number of primes around its approximation is rising proportionally to ( $R\left(c\right)$ ), the number of the series of multiples of primes, which are covering integer positions at this distance (c). The factor of proportionality ( $F_{SD\text{\_}\Delta \pi }=0.162389$ ) is again an inherent property of the primes.

Figure A4.1. Dispersion of the standard deviation of the dispersion of the number of primes around its average, the resulting constant value.

Annex A5. Evaluation of the Boundaries of the Dispersion

At the distance (c), with ( $R\left(c\right)$ ) being the number of the series of multiples of primes covering formerly free positions, the summing of the local density values over (j) is influenced only by ( $\sqrt{c}$ ). If for the distance succeeding primes were taken, as in the above evaluations, the size of the gaps between primes would account for the long-range fluctuations. If ( $R\left(c\right)$ ) changes by unity, there is a jump: At the change of the distance at certain number of primes ( $P_{\left(n\right)}$ ) the summation-limit changes from ( $R\left(c\right)$, $c=P_{\left(n\right)}$ ) to ( $R\left(c\right)+1$, $c=P_{\left(n+1\right)}$):

from ( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}$ ) to ( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)+1}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}$ ) (A5.1)

The difference makes

( $\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)+1}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}-\sqrt{c}{\displaystyle \underset{j=1}{\overset{R\left(c\right)}{\sum }}\frac{1}{\ln \left(j\sqrt{c}\right)}}\approx \frac{\sqrt{c}}{\ln \left(c\right)}=\frac{\sqrt{c}}{2\cdot \ln \left(\sqrt{c}\right)}=\frac{R\left(c\right)}{2}$ ). (A5.2)

For illustration, the discontinuity of the approximating function is shown. For this purpose, the values of the approximating function are evaluated in (addition to its sparse values evaluated in (1.4)) at distances corresponding to each prime ( $c=P_{\left(q\right)}$, ${\pi }_{appr\text{\_}tes{t}_{\left(q\right)}}={\pi }_{appr\text{\_}}\left(q\right)$ ) in the range ( $q=q_{low}\cdots q_{high}$ ):

from ( $q_{low}:=1909500$, $P\left(q_{low}\right)=30887083$ ) to ( $q_{high}:=1911600$, $P\left(q_{high}\right)=30923341$, $q:=q_{low}\cdots q_{high}$ )

${\pi }_{appr\text{\_}tes{t}_{\left(q\right)}}:={\pi }_{sec\text{\_}appr\text{\_}}\left[P_{\left(q\right)}\right]$ (A5.3)

The results are written to a file and are read from this file:

$\text{WRITEPRN}\left("\text{Nprime\_appr\_c}\text{.prn}"\right):={\pi }_{appr\text{\_}test}$ ; ${\pi }_{appr\text{\_}test}:=\text{READPRN}\left("\text{Nprime\_appr\_c}\text{.prn}"\right)$.

The discontinuity of the approximating function is shown in FigureA5.1. The size of the jumps (2.2) is the bandwidth of the dispersion due to the approximating function:

${\pi }_{bounds\text{\_}appr}\left(c\right)=\pm \frac{R\left(c\right)}{2}$ (A5.4)

Figure A5.1. Discontinuity due to the approximating function.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Titchmarsh, E.C. (1986) The Theory of the Riemann Zeta-Function. Oxford University Press, New York.
[2]	Pintz, J. (1980) On the Remainder Term of the Prime Number Formula II. On a Theorem of Ingham. Acta Arithmetica, 37, 209-220. https://doi.org/10.4064/aa-37-1-209-220
[3]	Platt, D.J. and Trudgian, T.S. (2021) The Error Term of the Prime Number Theorem. Mathematics of Computation, 90, 871-881. https://doi.org/10.1090/mcom/3583
[4]	Rosser, J.B. and Trudgian, T.S. (1941) Explicit Bounds for Some Functions of Prime Numbers. American Journal of Mathematics, 63, 211-232. https://doi.org/10.2307/2371291
[5]	Rosser, J.B. and Schoenfeld, L. (1962) Approximate Formulas for Some Functions of Primes. Illinois Journal of Mathematics, 6, 64-94. https://doi.org/10.1215/ijm/1255631807
[6]	Green, B. and Tao, T. (2007) The Primes Contain Arbitrary Long Arithmetic Progressions. Annals of Mathematics, 167, 481-547. https://doi.org/10.4007/annals.2008.167.481