1. Introduction
The general relativity theory describes the gravity field. However, the gravitational field quantizing leads to some problems: the strong nonlinearity of the gravity field leads to the impossibility of regularizing divergent diagrams, which number rises with increasing the order of the perturbation theory [1] [2] [3].
It is only in recent times, the theory of non-abelian fields gauge fields [4] [5] has played a significant role in the understanding of weak and strong nuclear forces [6] and raised hope of using similar methods for quantizing gravity fields; however, there is no any significant progress observed up-to-date in this direction [1] - [9].
Another problem originates in the field of classical physics of the particle system. Hamiltonian mechanics normally describes the system of particles, but Hamiltonian mechanics (the mechanics of conservative systems) is time-reversible. The universe based upon such Hamiltonian mechanics is either orbitally stable or is highly sensitive to the initial conditions [10] [11] in the presence of hyperbolic points. The system’s evolution is represented in the phase space by the Liouville equation, as the motion of an incompressible fluid: the phase space element can be deformed in as complex as it needs to be manner, but the measure, introduced in the phase space, is preserved. However, concurrently, the Second Law of Thermodynamics is valid here and determines the introduction of entropy: entropy in closed systems increases in an equilibrium state, reaching a maximum [11] [12]. Thus, time (chain of events) takes on a definite orientation: the system evolves from the “past” to the “future” from a state with lower entropy to a state with higher entropy. The transition to another dimensioned level of description—quantum mechanics—does not save the situation: the Schrödinger equation is reversible in time.
So far, it has not been possible to connect the Gibbs and Boltzmann distributions, in other words, to build up a microscopic theory of non-reversible processes, conciliating the contradictions of a number of fundamental physical principles within the standard presentations. Although, for example, a number of approaches present some features of interest, they do not solve problems for the complete phase space: irreversibility is observed only in Poincare sections at the introduction of the so-termed “K-flows” [10] [11] [12].
In [13] there another approach was implemented to observed irreversibility. It was proposed to revise the notion of time as a point on the real axis by introducing a fuzzy time as a set of real numbers with a finite membership function but not equal to unity, i.e., the concept of hazy or fuzzy-time. The fuzzy set
, where
is the membership function, which is further assumed to be continuously differentiable or finitely continuously differentiable and compact
, was considered instead of a C-number. The operation of defuzzification (weighing) by measure
determines the time
, which is further called macro time, and the difference
, we will call micro—or fuzzy-time. In the limiting case (classical interpretation of time), the measure
comes in proportion to the delta function. It was presumed that the system dynamics for a fuzzy time t follows from the standard variation principle of least action and is the usual Hamilton-Jacobi mechanics. This makes the transition to the limit from fuzzy mechanics to normal variational conservative mechanics correct for
. Further, the Liouvilleequation was solved by successive approximations, and the defuzzification field of the Liouville equation was reduced to a non-reversible equation. By formulating the fuzzy Pauli equation, a generalization was made for the quantum case. In both cases, the Second Law of Thermodynamics was derived by defuzzification of the fuzzy Liouville equation.
The presented work is devoted to the extension of the notion of fuzzy time to pseudo-Euclidean space. The concept of a fuzzy scalar field was introduced with a predefined measure of membership, for which there was determined the fuzzy Green’s function. Quantifying the fuzzy field was realized by defuzzification of the chronological ordering of the vacuum expectation of the integral of the exponential of the fuzzy field by the method of continuous integration. The irreversibility projection operator used earlier to formulate the fuzzy Boltzmann equation can be obtained as a passage to the limit to the slow motion of particles. It is fundamental that using the fuzzy Green’s function, the problem of regularization of divergences is solved in nonlinear theories, including quantizing the gravity field.
2. Green’s Function in a Fuzzy Space
Let us assume
as some function of time t. We introduce the
time shift operator
. If
is a Fourier
transform of the
function, then the Fourier transform is the following
:
. Now we will consider the fuzzy set
, where
is a measure of membership of the element x in a mathematical set Ω. By definition, the measure of membership, is positive
and
. For two sets A, B the following statement is true:
, if
. Further let us limit to the case of even measures
and for the measure
we assume
for any integer powers of n at
. Without loss of generality, we can put
.
Generalization of the basic classical rules of arithmetics to operations with fuzzy numerical sets or fuzzy-numbers and the introduction of the concepts of fuzzy-functions and fuzzy-relations were accomplished as follows. Initially we denote a fuzzy function with a measure
:
. And the corresponding explicit function will be denoted as
. Then function
, where
is the solution (possibly not the only one) of the equation
.
At that point,
. The expected value of a fuzzy-event (operation of defuzzification) has the following form:
(1)
Or in our case
(2)
In this expression,
,
—is the density of a fuzzy measure,
:
,
: and
—is a step function that provides the ability to integrate over the entire space.
The defuzzification Fourier transform has the form:
, (3)
where
—is the Fourier representation of a step function; a small component
describes the sense of first-order polarized rotation.
Thus we can make a point that fuzzy numerical set
with a measure of membership:
—is the sum of fuzzy numbers A and B. And fuzzy numerical set
with a measure of membership:
is the difference between fuzzy numbers A and B. The product and division of fuzzy numbers are determined in the same manner [14].
This let us define an important expression—the measure of the product
,
:
(4)
where
are the solutions to the equations
,
.
From here, it follows that defuzzification of the following expression
can be represented, with the consideration of (1), in the following form:
(5)
The external symbol
—designates the process of defuzzification.
Now, let us pass into a pseudo-Euclidean space with a metric
and denote x as
point in this space for which the fuzziness measure is equal to μ = 1 and
—which are the corresponding deviations with measure μ. We also assume
and the convergence of four-dimensional integral
for any n degree.
We will refer to a real scalar field in a fuzzy four-dimensional space with a fuzzy measure μ as is case with the one-dimensional field:
(6)
Let us appropriate that the field
satisfies the wave equation:
(7)
The proper Green’s function in k-space has the standard form [7] [15]:
(8)
For quantizing the fuzzy field, it is necessary to defusify the chronological ordering of the integral vacuum expectation over the fuzzy exponent:
(9)
In this expression
—is the usual explicit function of a variable x, the symbol
means the vacuum average.
The vacuum expectation of chronological ordering for explicit fields begets the form, known from [2] [3]:
(10)
Further computations can be conveniently produced using the model of continual integration for which we should first pass into the discrete impulse space by specifying: ∆k—as element of (4-th) volume,
,
,
,
. Considering
as a real function, we can take
. Then the expression (9), knowing (10) in the discrete representation, will have the form:
(11)
Denoting
,
and using the known integral:
(12)
The expression transforms into:
The value
, with the regard of (4), at substitution of discrete summation through integrating can be represented as:
(13)
Using the expression for the standard measure of continual integration [7] and expression (11), we can derive the following expression for the defusified measure:
(14)
and represent it in the form:
, (15)
where
,
,
.
At this point, the defuzzified chronological ordering for any composite function can be written as:
(16)
The only significant difference from the known relations—consists in the definition of a metric after the process of defuzzification in k-space through an adequate propagator:
(17)
In the context of the Non-Quantized System N of interacting particles, which was described in [13], we write the Liouville equation in the form:
(18)
where
.
—are momentum and coordinate of a particle, V—is a pair interaction potential.
The Hermitian operator
, its proper functions:
, (19)
where k—is the wave propagation vector, n—is a particle number, which are orthogonal and can be used as a normal orthogonal basis.
The Green’s function of an unbound particle in the explicit case after the Fourier conversion takes the form:
(20)
In this expression, the mass of the particle m is assumed equal.
After replacing
and fuzzifying the explicit delta functions using the relation:
, after defuzzification and integrating over 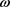 we will have:
we will have:
(21)
Integrating over a space variable
will give us an unessential constant, which will be decreased upon normalizing in calculations of a number of perturbations in [13]; the remaining expression exactly coincides with the operator of damping projection, which reduces the reversible Liouville equation to a type of noninvertible Boltzmann equation or the fuzzy Pauli equation for a system of quantum particles [13].
3. The Fuzzy Causality Principle for a Field
If X is a fuzzy set with a measure
, then we may call an aggregate of points x for which the measure
,
as an almost positive fuzzy interval with
level, i.e. the range of values of x for which the minimum x with measure
is positive. The work [13] contains the formulated principle of fuzzy causality for a Non-quantized system in fuzzy time: the events related to fuzzy time points
and
at one or close spatial points can be associated with an unconditional causal link with the level
, if the fuzzy interval between them is almost positive. Otherwise, they are bound by a conditional causal link with the level
.
Now, let us formulate this principle for a field in a linear 4-dimensional space. From the expression (18), we have obtained an adequate propagator in a clearly defined coordinate space in the following form after defuzzification:
(22)
The propagator
has the known form [7] [15]:
, (23)
where
,
—are the Bessel, Neumann and Hankel functions, respectively.
Now, in a fuzzy space inside a light cone (luminous cone)
:
(24)
where
—are the coefficients of convolution of the measure of uncertainty in terms of the Bessel and Neumann functions, respectively:
(25)
On the light cone
, the defuzzified propagator can be integrated over
. Now it does not have the peculiarities inherent in conventional quantized field theory:
(26)
The expansion
near the light cone takes the form:
(27)
This expression does not take into account the exceptions
and summands of order
and higher. Therefore, outside the light cone
:
(28)
In the comparison of the definition of the fuzzy causality principle, we may affirm that case (26) corresponds to unconditional fuzzy link, and case (28)—to the conditional causality link. The confidence level
, introduced in [13] is determined by a particular type of measure of membership. Once again, conditional causality link has no classical analogs: the “past” in it may depend on the “future,” and the mere notions of “past” and “future” may lack definite meaning. Interesting analogies arise with the results of [13]. Here the generalizations to a system of complex conjugate fields, vector, and tensor fields become apparent.
4. Regularization of Divergences
In the calculation of the full Green’s functions in Standard Quantized Field Theory, divergences occur at
in the calculation of self-energy corrections Σ(k). Methods of mass or dimensional regularization (ε—expansion) are mainly used to eliminate them. The reason for these divergences is the uncertainty of the propagator at
[7] [15]. Fuzzy field theory does not have this problem. Indeed, we will analyze a fuzzy theory of an interacting field
with
an interaction Lagrangian
, where g—is some constant. Particularly—the energy part of the second order of interaction now takes the form:
(29)
and, following the assumption about the nature of the measure of fuzziness, this energy part is always regular.
The specific form of this integral depends on the nature of the measure and, in some cases, can be thoroughly calculated.
Regularity of all expressions of this type:
(30)
allows us to regularize a theory of any order, including a possibility of fuzzy quantization of the gravity field.
5. Discussion of Results
In conjunction with the data [13], the obtained results demonstrated an opportunity to solve a number of problems in a same way, using the concept of fuzzy space, basically, problems of irreversibility in classical mechanics, in particular, the transition from the reversible Liouville equation to the irreversible Boltzmann equation by the other methods than used in the approach [6]. On top of that, first, we can substantiate the second law of thermodynamics from the first principles with a possibility to extend to the noninvertible Pauli equation; second, we can develop an algorithm for field quantization in a fuzzy space, using the defusified Green’s influence function (propagator), and to extend the principle of fuzzy causality to field theory; third, we are able to solve the problem for regularization of divergent integrals by formulating a full Green function in the theory of a fuzzy field of a random order
. In a conventional quantum field theory, it is possible to demonstrate the ability to regularize theories of order not higher than four (4), using ε-expansion as an example. In particular, it makes possible to quantize a fuzzy gravity field. This lets us to demonstrate the identity of the gravitational and stationary mass as well. As reasonably shown in [16], in the conventional Poincare-Einstein Theory of General Relativity, such transformation of spatial coordinates, in which the stationary mass can take any (including negative!) value, is possible in a static, centrally symmetrical case. Quantization in fuzzy space, in any order of the perturbation theory, makes these masses identical.
The simultaneous achievement of these results is possible at the transition from the concept of a clearly-defined space to a fuzzy space, using a different arithmetics and, accordingly, analysis. In any alternate methods of generalizing the union or intersection operators of fuzzy sets, for example, Yager et al. (with nonparametric t and S norm functions) [14] for the formulation of fuzzy arithmetics and analysis, the results will be the same.
With the transition to a clearly defined (explicit) space
, these problems and contradictions will arise again. In this sense, the concept of fuzzy space is the only acceptable and simple concept that resolves such contradictions in a common way.
6. Conclusions
1) The concept of a fuzzy field was introduced in pseudo-Euclidean space.
2) There was formulated the defuzzified Green’s function of the fuzzy field, and its behavior was scrutinized inside and outside the light cone. Also, here was analyzed the transition to the Green’s function of the Non-quantized (classical) n-particle system. The problem of regularization of divergences was discussed with introduction of a defuzzified Green’s function.
3) The fuzzy causality principle in pseudo-Euclidean space was formulated for the limit case of slow processes with the transition to the conventional fuzzy causality principle, considered earlier.